CM4 - La 🏺boîte de Pandore🏺 des approximations

Selon Hésiode, lorsque Prométhée déroba le feu du ciel, Zeus, le roi des dieux, se vengea en offrant Pandore à Épiméthée, le frère de Prométhée. Pandore, poussée par la curiosité, ouvrit une jarre qui lui avait été confiée, libérant ainsi la maladie, la mort et d’innombrables maux dans le monde. En refermant précipitamment le récipient, elle découvrit qu’une seule chose y demeurait : l’espoir. C’est de cette légende qu’est née l’expression « ouvrir la boîte de Pandore », symbolisant le fait de déclencher une série de problèmes imprévus et incontrôlables.

Pandora

De manière similaire, le domaine des approximations numériques peut être perçu comme une boîte de Pandore. En s’aventurant dans ce champ, on se confronte à une multitude de défis, tels que la stabilité, les problèmes raides et les systèmes mal conditionnés. Chacun de ces aspects représente un défi à surmonter pour obtenir des résultats fiables et précis.

%reset -f
%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
plt.rcParams.update({<span class="st">'font.size'</span>: <span class="dv">12</span>})

from scipy.optimize import fsolve

import sympy as sym
sym.init_printing()

from IPython.display import Markdown

Plan d’étude

Ce chapitre est divisé en deux parties principales :

• PARTIE 1️⃣ Propriétés du problème de Cauchy :
  1. existence et unicité de la solution,
  2. dépendance continue par rapport aux données initiales,
  3. conditionnement (et lien avec des problèmes stiffs) ;
• PARTIE 2️⃣ Propriétés des schémas numériques :
  1. convergence (et ordre de convergence) à travers les deux notions de
     • consistance (et ordre de consistance),
     • zéro-stabilité (stabilité sur un intervalle de temps fini)
  2. absolue-stabilité (stabilité sur un intervalle de temps infini) et lien avec les problèmes stiffs.

1 PARTIE 1️⃣ - propriétés du problème de Cauchy : bien posés (mathématiquement et numériquement), bien conditionnés

En général, il ne suffit pas qu’un schéma numérique soit convergent pour qu’il donne de bons résultats sur n’importe quelle équation différentielle. Dès qu’on tente d’approcher une solution, de nombreux facteurs peuvent en fait nous en éloigner : une étude mathématique sophistiquée doit alors être envisagée. En particulier, il faut que le problème de Cauchy soit

• mathématiquement bien posé : sa solution existe et est unique,
• numériquement bien posé : sa solution n’est pas trop perturbée par une erreur initiale ou des perturbations du second membre,
• bien conditionné (= non raide) : les méthodes numériques usuelles peuvent calculer une solution approchée raisonnable en un nombre raisonnable d’itérations.

Ces définitions sont celles adoptés aux pages 235-236 dans le livre de Jean-Pierre DEMAILLY, Analyse Numérique et équations différentielles.

1.1 Problème mathématiquement bien posé : existence et unicité de la solution

Définition de problème mathématiquement bien posé

On dit qu’un problème de Cauchy est mathématiquement bien posé s’il existe une et une seule solution.

Si ce n’est pas le cas, on dit qu’il est mathématiquement mal posé.

Exemple de problème mathématiquement MAL posé

Le problème de Cauchy

\( \begin{cases} y'(t) = \sqrt[3]{y(t)}, & \text{pour } t>0,\\ y(0) = 0. \end{cases} \)

ne satisfait pas les hypothèses du théorème de Cauchy-Lipschitz, car la fonction \(\varphi(t,y)=\sqrt[3]{y}\) n’est pas lipschitzienne par rapport à la deuxième variable en \(y=0\) (on a \(\partial_y \varphi(t,y)=\frac{1}{3\sqrt[3]{y^2}} \xrightarrow[y\to0]{}+\infty\)).
On ne peut donc pas garantir l’unicité de la solution et, en effet, il est simple de vérifier que, pour tout \(t\ge0\), les trois fonctions

• \(y_1(t)=0\) pour tout \(t\)
• \(y_{2,3}(t)=\pm\sqrt{\frac{8}{27}t^3}=\pm\frac{2\sqrt{2}}{3\sqrt{3}}\sqrt{t^3}=\pm\frac{2\sqrt{6}}{9}\sqrt{t^3}\)

sont solution du problème de Cauchy donné.

Dans ce cas, lorsqu’on utilise une méthode numérique, on ne peut pas savoir quelle solution ce schéma approche et différents schémas peuvent approcher différentes solutions.

# Remaruqe : si on demande à sympy de calculer toutes les solutions, il ne trouve pas la solution constante = 0
t = sym.Symbol('t')
y = sym.Function('y')

edo = sym.Eq( sym.diff(y(t),t) , y(t)**(1/sym.S(3))  )
display(edo)

solgenLIST = sym.dsolve(edo,y(t))
display(solgenLIST)

for solgen in solgenLIST:
    t0, y0 = 0, 0
    consts = sym.solve( [solgen.rhs.subs(t,t0)-y0 ], dict=True)[0]
    solpar = solgen.subs(consts).simplify()
    display(solpar)

\(\displaystyle \frac{d}{d t} y{\left(t \right)} = \sqrt[3]{y{\left(t \right)}}\)

\(\displaystyle \left[ y{\left(t \right)} = - \frac{2 \sqrt{6} \left(C_{1} + t\right)^{\frac{3}{2}}}{9}, \ y{\left(t \right)} = \frac{2 \sqrt{6} \left(C_{1} + t\right)^{\frac{3}{2}}}{9}\right]\)

\(\displaystyle y{\left(t \right)} = - \frac{2 \sqrt{6} t^{\frac{3}{2}}}{9}\)

\(\displaystyle y{\left(t \right)} = \frac{2 \sqrt{6} t^{\frac{3}{2}}}{9}\)

Exercice : problème MAL posé mathématiquement

• Montrer que le problème de Cauchy suivant admet une infinité de solutions de classe \(\mathcal{C}^1(\mathbb{R})\):

\( \begin{cases} y'(t)=2\sqrt{|y(t)|}, & t>0\\ y(0)=0. \end{cases}\)

• Parmi ces solutions, quelle solution approche-t-on si on utilise la méthode d’Euler explicite? et la méthode d’Euler implicite?
  
• Que se passe-t-il si la donnée initiale est \(y(0)=y_0>0\)?

Correction

Sur \(\mathbb{R}^+\) la fonction \(\varphi(t,y)=2\sqrt{y}\) n’est pas lipschitzienne par rapport à \(y\) au voisinage de \((t,0)\) (car \(\partial_y\varphi=1/\sqrt{y}\to\infty\) lorsque \(y\to0\)), donc le théorème d’existence et unicité locale n’est pas valable au voisinage de \((0,0)\). Même raisonnement sur \(\mathbb{R}^-\).

L’EDO est à variables séparables, on peut donc calculer explicitement toutes les solutions du problème de Cauchy :

• elle admet une seule solution constante, la fonction \(y(t)=0\) pour tout \(t\in\mathbb{R}^+\),
• et des solutions de la forme \(y(t)=(t+c)^{2}\) pour tout \(t\ge c\).

En imposant la CI on trouve que, pour tout \(b\in\mathbb{R}^+\), les fonctions

\( y_b(t)= \begin{cases} 0 , &\text{si }0\le t\le b, \\ (t-b)^{2} , &\text{si }t\ge b, \end{cases} \)

sont de classe \(\mathcal{C}^1(\mathbb{R}^+)\) et sont solution du problème de Cauchy donné.

# Remaruqe : si on demande à sympy de calculer les solutions, il donne une réponse enigmatique
# ===============================================================================================


t = sym.Symbol('t')
y = sym.Function('y')


display(Markdown("**Problème de Cauchy**"))
edo = sym.Eq( sym.diff(y(t),t) , 2*sym.sqrt(abs(y(t)))  )
display(edo)

t0, y0 = 0, 0
display(sym.Eq(y(t0),y0))

# Méthode directe
display(Markdown("**Méthode directe**"))
sol = sym.dsolve(edo,y(t), ics={y(t0):y0})
display(sol)

# Méthode pas à pas
display(Markdown("**Méthode pas à pas**"))
solGEN = sym.dsolve(edo,y(t))
display(solGEN)
consts = sym.solve( [solGEN.rhs.subs(t,t0)-y0 ], dict=True)[0]
solPAR = solGEN.subs(consts).simplify()
display(solPAR)

Problème de Cauchy

\(\displaystyle \frac{d}{d t} y{\left(t \right)} = 2 \sqrt{\left|{y{\left(t \right)}}\right|}\)

\(\displaystyle y{\left(0 \right)} = 0\)

Méthode directe

\(\displaystyle \int\limits^{y{\left(t \right)}} \frac{1}{\sqrt{\left|{y}\right|}}\, dy = 2 t + \int\limits^{0} \frac{1}{\sqrt{\left|{y}\right|}}\, dy\)

Méthode pas à pas

\(\displaystyle \int\limits^{y{\left(t \right)}} \frac{1}{\sqrt{\left|{y}\right|}}\, dy = C_{1} + 2 t\)

\(\displaystyle 2 t = \int\limits^{y{\left(t \right)}} \frac{1}{\left|{\sqrt{y}}\right|}\, dy\)

Traçons quelques courbes :

xx = np.linspace(0,2,101)
yyr = np.zeros_like(xx)

# f = lambda x,b : 0 if (x<=b) else (x-b)**2
# yy1 = [f(x,1)    for x in xx]
# yy75= [f(x,0.75) for x in xx]
# yy0 = [f(x,0)    for x in xx]

f = lambda x, b : np.where(x<=b, 0, (x-b)**2)
yy1 = f(xx,1)
yy75= f(xx,0.75)
yy0 = f(xx,0)

plt.figure(figsize=(8,5))
plt.plot(xx,yyr  ,'r-', label=r'$y(t)=0$ $\forall$ $t$')
plt.plot(xx,yy1  ,'b:', label=r'$y_{b=1}(t)$')
plt.plot(xx,yy75 ,'g*', label=r'$y_{b=0.75}(t)$')
plt.plot(xx,yy0  ,'yd', label=r'$y_{b=0}(t)$')
plt.legend();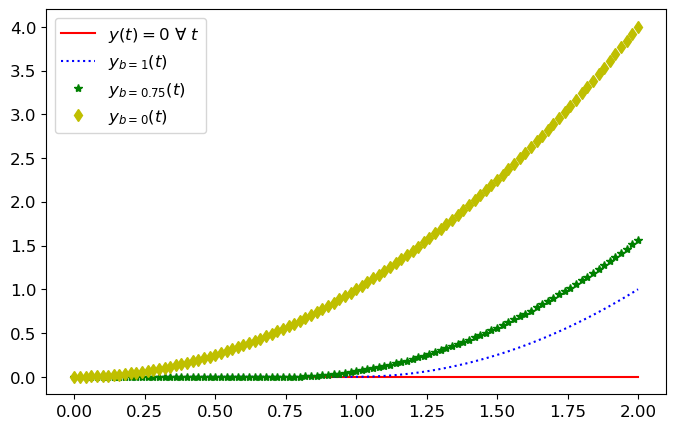

La méthode d’Euler explicite construit la suite

\(\begin{cases} u_0=y_0=0,\\ u_{n+1}=u_n+h \varphi(t_n,u_n)=u_n+hu_n^{1/2},& n=0,1,2,\dots N_h-1 \end{cases}\)

par conséquent \(u_n=0\) pour tout \(n\): la méthode d’Euler explicite approche la solution constante \(y(t)=0\) pour tout \(t\in\mathbb{R}^+\).

La méthode d’Euler implicite construit la suite

\(\begin{cases} u_0=y_0=0,\\ u_{n+1}=u_n+h \varphi(t_{n+1},u_{n+1})=u_n+hu_{n+1}^{1/2},& n=0,1,2,\dots N_h-1. \end{cases}\)

par conséquent \(u_0=0\) mais \(u_1\) dépend de la méthode de résolution de l’équation implicite \(x=0+h\sqrt{x}\). Bien-sûr \(x=0\) est une solution mais \(x=h^{2}\) est aussi solution. Si le schéma choisit \(u_1=h^{2}\), alors \(u_n>0\) pour tout \(n\in\mathbb{N}^*\).

Notons que le problème de Cauchy avec une CI \(y(0)=y_0>0\) admet une et une seule solution, la fonction \(y(t)=\frac{1}{4}(t+2\sqrt{y_0})^{2}\). Dans ce cas, les deux schémas approchent la même unique solution.

1.2 Problème numériquement bien posé : dépendance continue de la solution par rapport aux données.

Une fois calculée la solution numérique \(\{u_n\}_{n=0}^{N}\) d’un problème de Cauchy mathématiquement bien posé, il est légitime de chercher à savoir dans quelle mesure l’erreur \(|y(t_n)-u_n|\) est petite. Cela dépend bien sur du schéma choisi, mais aussi du problème en question. En effet, étant donné que les erreurs d’arrondi amènent toujours à résoudre un problème perturbé, il est important de savoir si la solution d’un problème perturbé est proche de la solution du problème non perturbé.

Définition de problème numériquement bien posé

On dit qu’un problème de Cauchy est numériquement bien posé si la solution d’un problème faiblement perturbé (second membre ou condition initiale) possède une solution proche de celle du problème original.

Si ce n’est pas le cas, on dit qu’il est numériquement mal posé.

Question pratique : Généralement on utilise un schéma pour approcher la solution d’un problème dont on ne connait pas la solution exacte. Comment peut-on conjecturer que le problème est numériquement mal posé ?

Idée : on teste un même schéma avec différentes discrétisations (très différentes entre elles) ou on teste différents schémas. Si les solutions obtenues sont très différentes, le problème est probablement numériquement mal posé.

Exemple de problème BIEN posé numériquement

Soit \(y_0\) donné et considérons une petite perturbation \(\varepsilon\). Calculons \(\lim_{t\to+\infty} y_{\varepsilon}\) où \(y_{\varepsilon}\) est la solution exacte du problème de Cauchy

\(\begin{cases} y_{\varepsilon}'(t) = -y_{\varepsilon}(t), &\forall t>0,\\ y_{\varepsilon}(0) = y_0+\varepsilon. \end{cases}\)

La solution exacte est \(y(t)=y_0e^{-t}+\varepsilon e^{-t}\) : l’effet de la perturbation \(\varepsilon\) s’atténue lorsque \(t\to+\infty\) puisque \(\varepsilon e^{-t}\xrightarrow[t\to+\infty]{}0\).
Cela suggère que si une erreur est faite dans une étape d’une méthode d’itération, l’effet de cette erreur s’atténue au cours du temps: le problème est numériquement bien posé.

y0 = 1

y = lambda t,eps : (y0+eps)*np.exp(-t)

tt  = np.linspace(0,5,101)
yye = y(tt,0.1) # [y(t,0.1) for t in tt]
yy0 = y(tt,0)   # [y(t,0) for t in tt]

plt.figure(figsize=(8,5))
plt.plot(tt,yye, label="$y(0)=1.1$")
plt.plot(tt,yy0, label="$y(0)=1$")
plt.legend(bbox_to_anchor=(1,1));
plt.axis([0,5,0,1.1]);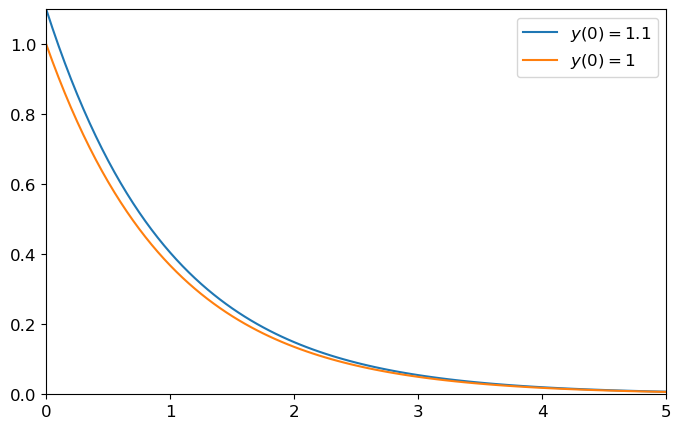

Exemple de problème BIEN posé numériquement

Considérons le problème de Cauchy \(\begin{cases} y'(t) = y(t)\sin(t), &\forall t>0,\\ y(0) = -1+\varepsilon. \end{cases}\)

La solution est \(y(t)=-e^{1-\cos(t)}+\varepsilon e^{1-\cos(t)}\) : l’effet de la perturbation \(\varepsilon\) reste borné lorsque \(t\to+\infty\) puisque \(|\varepsilon e^{1-\cos(t)}|\le \varepsilon e^2\). Cela suggère que si une erreur est faite dans une étape d’une méthode d’itération, l’effet de cette erreur reste borné au cours du temps: le problème est numériquement bien posé.

y0 = -1

y = lambda t,eps : (y0+eps)*np.exp(1-np.cos(t))

tt = np.linspace(0,40,401)
yye = y(tt,0.1) # [y(t,0.1) for t in tt]
yy0 = y(tt,0)   # [y(t,0) for t in tt]

plt.figure(figsize=(10,5)) 
plt.plot(tt,yye,label="$y(0)=-0.9$")
plt.plot(tt,yy0,label="$y(0)=-1$")
plt.legend(bbox_to_anchor=(1,1));

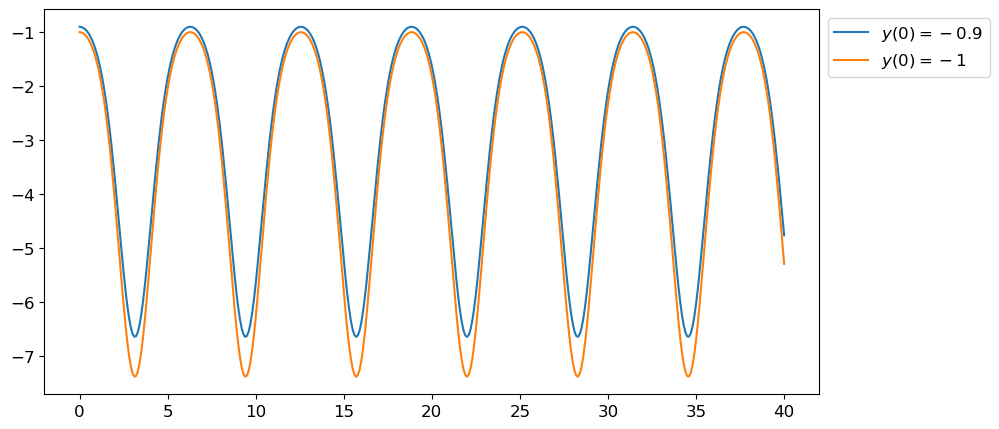
Exemple de problème MAL posé numériquement

Considérons le problème de Cauchy

\(\begin{cases} y'(t) = y(t), &\forall t>0,\\ y(0) = y_0+\varepsilon. \end{cases}\)

La solution est \(y(t)=y_0e^{t}+\varepsilon e^{t}\) : l’effet de la perturbation \(\varepsilon\) s’amplifie lorsque \(t\to+\infty\) puisque \(\varepsilon e^{t}\xrightarrow[t\to+\infty]{}+\infty\). Cela suggère que si une erreur est faite dans une étape d’une méthode d’itération, l’effet de cette erreur s’amplifie au cours du temps: le problème est numériquement mal posé.

y0 = 0

y = lambda t,eps : (y0+eps)*np.exp(t)

tt  = np.linspace(0,5,101)
yye = y(tt,0.01) # [y(t,0.01) for t in tt]
yy0 = y(tt,0)    # [y(t,0) for t in tt]

plt.figure(figsize=(8,5)) 
plt.plot(tt, yye, lw='2', label="$y(0)=0.01$")
plt.plot(tt, yy0, lw='5', label="$y(0)=0$")
plt.legend(bbox_to_anchor=(1,1))
plt.axis([0,5,0,1.1]);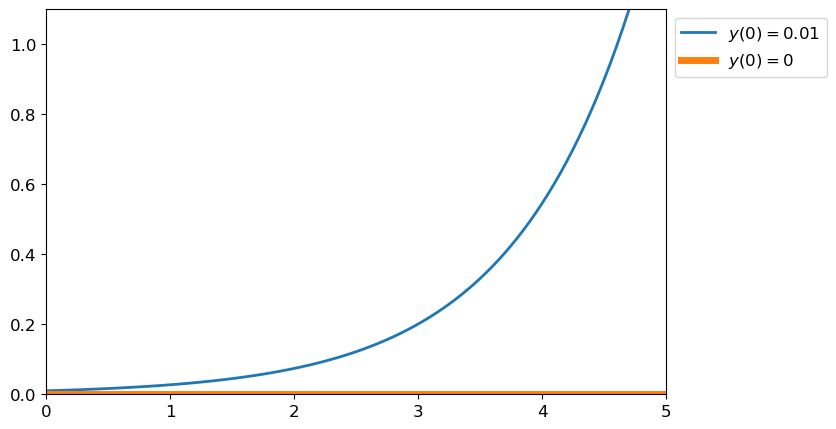

Exemple de problème MAL posé numériquement

Soit \(\alpha\) un nombre quelconque. Étudions la solution exacte \(y_{\alpha}\) du problème de Cauchy

\( \begin{cases} y_{\alpha}'(t) = 3y_{\alpha}(t)-3t, &\forall t\in\mathbb{R},\\ y_{\alpha}(0) = \alpha. \end{cases} \)

Comparons ensuite les solutions \(y_{1/3}\) et \(y_{0.333333}\) en \(t=10\).

La solution, définie sur \(\mathbb{R}\), est donnée par

\( y_{\alpha}(t)=\left(\alpha-\frac{1}{3}\right)e^{3t}+t+\frac{1}{3}. \)

Évaluons \(y_{\alpha}\) en \(t=10\):

• si \(\alpha=\frac{1}{3}\) alors \(y_{\alpha}(10)=\frac{31}{3}\),
• si \(\alpha=0.333333\) alors \(y_{\alpha}(10)=(0.333333-1/3)e^{30}+10+1/3=-e^{30}/3000000+31/3\approx31/3+10^7/3\).

Conséquence : si nous faisons le calcul avec l’approximation \(\alpha=0.333333\) au lieu de \(1/3\), nous avons \(y(10)=31/3-e^{30}/3000000\) ce qui représente une différence avec la précédente valeur de \(e^{30}/3000000\approx10^7/3\).

Cet exemple nous apprend qu’une petite erreur sur la condition initiale (erreur relative d’ordre \(10^{-6}\)) peut provoquer une très grande erreur sur \(y(10)\) (erreur relative d’ordre \(10^{6}\)). Ainsi, si le calculateur mis à notre disposition ne calcule qu’avec \(6\) chiffres significatifs (en virgule flottante), alors \(\alpha=1/3\) devient \(\alpha=0.333333\) et il est inutile d’essayer d’inventer une méthode numérique pour calculer \(y(10)\). En effet, la seule erreur sur la condition initiale provoque déjà une erreur inadmissible sur la solution. Nous sommes en présence ici d’un problème numériquement mal posé

Vérifions-le avec sympy :

t = sym.Symbol('t')
y = sym.Function(r'y_{\alpha}')

edo = sym.Eq( sym.diff(y(t),t) , 3*y(t)-3*t  )
#display(edo)

solgen = sym.dsolve(edo,y(t))
#display(solgen)

alpha = sym.Symbol('alpha')
t0, y0 = 0, alpha
consts = sym.solve( [solgen.rhs.subs(t,t0)-y0 ], dict=True)[0]
solpar = solgen.subs(consts).simplify()
display(solpar)

sol1 = solpar.subs(t,10).subs(alpha,sym.Rational(1,3))
sol2 = solpar.subs(t,10).subs(alpha,0.333333)
display(sol1)
display(sol2)
print('Difference:')
display((sol1.rhs-sol2.rhs).evalf())

\(\displaystyle y_{\alpha}{\left(t \right)} = t + \left(\alpha - \frac{1}{3}\right) e^{3 t} + \frac{1}{3}\)

\(\displaystyle y_{\alpha}{\left(10 \right)} = \frac{31}{3}\)

\(\displaystyle y_{\alpha}{\left(10 \right)} = \frac{31}{3} - 3.33333333324415 \cdot 10^{-7} e^{30}\)

Difference:

\(\displaystyle 3562158.19374618\)

Exercice : problème numériquement MAL posé à la précision machine

On considère un problème de Cauchy dépendant d’un paramètre \(\varepsilon\) et on note \(y_\varepsilon(t)\) sa solution. Estimer la différence en \(t=50\) entre les solutions \(y_{\varepsilon}\) avec \(\varepsilon=10^{-17}\) et \(\varepsilon=0\) :

\( \begin{cases} y_\varepsilon'(t)=5y_\varepsilon(t)-5, &t\in[0;50]\\ y_\varepsilon(0)=1+\varepsilon. \end{cases} \)

Notons que \(\varepsilon=10^{-17}\) est une valeur très proche de \(0\) et correspond à l’erreur d’arrondi d’un calculateur qui travaille avec \(17\) chiffres significatifs.

La solution exacte est donnée par \(y_\varepsilon(t)=\varepsilon e^{5t}+1\) comme on peut le vérifier avec sympy :

import sympy as sym
import numpy as np
import matplotlib.pyplot as plt

# Définition des symboles
t = sym.Symbol('t')
epsilon = sym.Symbol(r'\varepsilon')

# Définition de la fonction y(t)
y = sym.Function(r'y_{\varepsilon}')(t)

# Équation différentielle
edo = sym.Eq(sym.diff(y, t), 5*y - 5)
display(edo)

# Condition initiale
display( sym.Eq(y.subs(t, 0), 1 + epsilon))

# Résolution
sol = sym.dsolve(edo, y, ics={y.subs(t, <span class="dv">0</span>): <span class="dv">1</span> <span class="op">+</span> epsilon})
display(sol)

# Calcul des solutions pour epsilon=10^(-17) et epsilon=0
sol1 = sol.subs({t: <span class="dv">50</span>, epsilon: sym.Rational(<span class="dv">1</span>, <span class="dv">10</span><span class="op">**</span><span class="dv">17</span>)})
sol0 = sol.subs({t: <span class="dv">50</span>, epsilon: <span class="dv">0</span>})
display(sol1)
display(sol0)

# Affichage de la différence entre les solutions
print('Difference:')
display((sol1.rhs - sol0.rhs).evalf())

\(\displaystyle \frac{d}{d t} y_{\varepsilon}{\left(t \right)} = 5 y_{\varepsilon}{\left(t \right)} - 5\)

\(\displaystyle y_{\varepsilon}{\left(0 \right)} = \varepsilon + 1\)

\(\displaystyle y_{\varepsilon}{\left(t \right)} = \varepsilon e^{5 t} + 1\)

\(\displaystyle y_{\varepsilon}{\left(50 \right)} = 1 + \frac{e^{250}}{100000000000000000}\)

\(\displaystyle y_{\varepsilon}{\left(50 \right)} = 1\)

Difference:

\(\displaystyle 3.74645461450267 \cdot 10^{91}\)

Une très petite erreur sur la condition initiale (de l’ordre de la précision machine) provoque une très grande erreur sur \(y(50)\). Ainsi, il est inutile d’essayer d’inventer une méthode numérique pour calculer \(y(50)\). En effet, la seule erreur sur la condition initiale provoque déjà une erreur inadmissible sur la solution. Nous sommes en présence ici d’un problème numériquement mal posé

Exercice : problème numériquement MAL posé

L’objectif de cet exercice est de bien mettre en évidence l’influence d’une petite perturbation de la condition initiale sur la solution d’un problème numériquement mal posé et d’appliquer la méthode d’Euler explicite pour en approcher la solution exacte.

Considérons le problème de Cauchy

\(\begin{cases} y'(t)=3\dfrac{y(t)}{t}-\dfrac{5}{t^3},\\ y(1)=a \end{cases}\)

1. Calculer l’unique solution exacte à ce problème de Cauchy en fonction de \(a\) pour \(t>0\). Remarquer qu’avec le changement de variable \(u(t)=\frac{y(t)}{t}\) on obtient une EDO linéaire d’ordre 1.
2. Tracer la solution exacte sur l’intervalle \([1;5]\) pour \(a=1\), \(a=1\pm\frac{1}{1000}\) et \(a=1\pm\frac{1}{100}\).
3. Pour \(a=1\), sur un autre graphique tracer la solution exacte et les solutions obtenues par la méthode d’Euler explicite avec \(N=20\), \(N=100\), \(N=300\), \(N=5000\). Comment expliquez-vous ce comportement du schéma?

Correction

Calculons les solutions de l’edo pour \(t>0\). On pose \(u(t)=\frac{y(t)}{t}\) ainsi \(y(t)=tu(t)\) et \(y'(t)=u(t)+tu'(t)\). On obtient l’edo linéaire d’ordre 1 suivante: \( tu'(t)-2u(t)=-5t^{-3}. \) On a \(a(t)=t\), \(b(t)=-2\) et \(g(t)=-5t^{-3}\) donc
+ \(A(t)=\int \frac{b(t)}{a(t)}\mathrm{d}t=\int -\frac{2}{t}\mathrm{d}t= -2\ln(t)=\ln(t^{-2})\), + \(B(t)=\int \frac{g(t)}{a(t)}e^{A(t)}\mathrm{d}t=\int -5t^{-4} e^{A(t)}\mathrm{d}t=\int -5t^{-6} \mathrm{d}t = t^{-5}\).

On conclut que \(u(t)=ce^{-A(t)}+B(t)e^{-A(t)}=ct^2+t^{-3}\) et \(\boxed{y(t)=tu(t)=ct^3+t^{-2}}\).

En imposant la condition \(a=y(1)\) on trouve l’unique solution du problème de Cauchy donné: \( y(t)=(a-1)t^3+\dfrac{1}{t^2}. \)

Vérifions ce calcul avec sympy:

t = sym.Symbol('t')
y = sym.Function('y')

edo = sym.Eq( sym.diff(y(t),t) ,  3*y(t)/t-5/t**3  )
display(edo)

solgen = sym.dsolve(edo,y(t))
display(solgen)

a = sym.Symbol('a')
t0, y0 = 1, a
consts = sym.solve( [solgen.rhs.subs(t,t0)-y0 ], dict=True)[0]
solpar = solgen.subs(consts)
display(solpar)

\(\displaystyle \frac{d}{d t} y{\left(t \right)} = \frac{3 y{\left(t \right)}}{t} - \frac{5}{t^{3}}\)

\(\displaystyle y{\left(t \right)} = \frac{C_{1} t^{5} + 1}{t^{2}}\)

\(\displaystyle y{\left(t \right)} = \frac{t^{5} \left(a - 1\right) + 1}{t^{2}}\)

Traçons les solutions exactes pour \(a=1\), \(a=1\pm\frac{1}{1000}\) et \(a=1\pm\frac{1}{100}\) sur l’intervalle \([1;5]\) :

sol_exacte = lambda t,y0 : (y0-1)*t**3+1/t**2

# INITIALISATION
t0     = 1
tfinal = 5
c = 1

tt = np.linspace(t0,tfinal,101)
Y0 = [c+1.e-2,c+1.e-3,c,c-1.e-3,c-1.e-2]

plt.figure(figsize=(10,7))
for y0 in Y0:
    yy = sol_exacte(tt,y0) # [sol_exacte(t,y0) for t in tt] 
    plt.plot(tt, yy, label=f'$y_0={</span>y0<span class="sc">}$')
plt.legend(bbox_to_anchor=(1.05, 1), loc='upper left')
plt.grid()
plt.title('Solutions exactes pour differents valeurs de $y_0$')
plt.axis([t0,tfinal,-c,c]);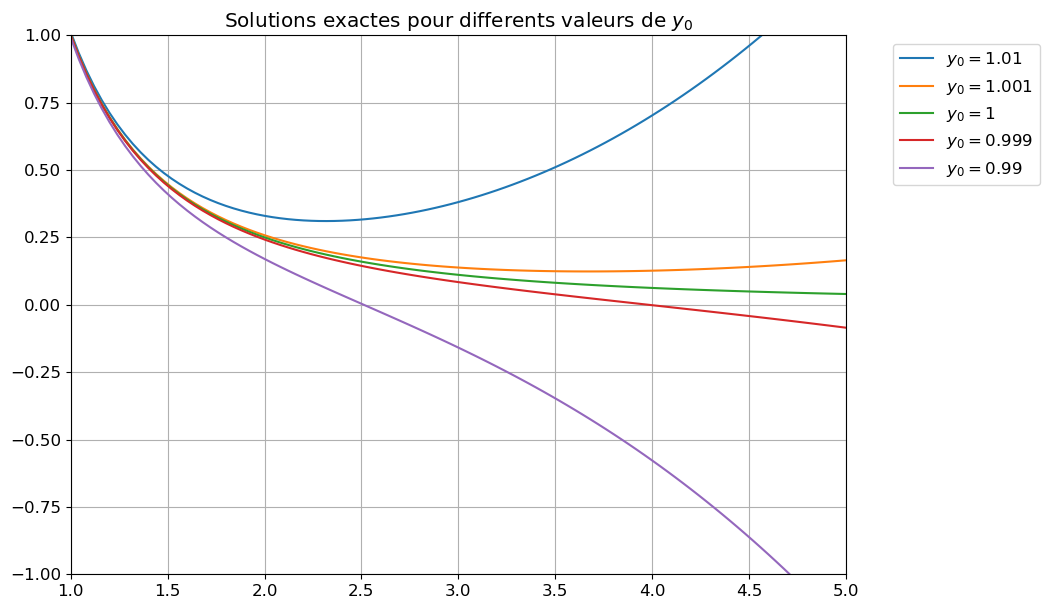

On constate qu’une petite perturbation de la condition initiale entraîne une grosse perturbation de la solution, en effet \( \lim_{t\to+\infty}y(t)= \begin{cases} +\infty &\text{si } a>1,\\ 0^+ &\text{si } a=1,\\ -\infty &\text{si } a<1. \end{cases} \)
Si \(a=1\), la solution exacte est \(y(t)=t^{-2}\) mais le problème est numériquement mal posé car toute (petite) erreur de calcul a le même effet qu’une perturbation de la condition initiale: on “réveille” le terme dormant \(t^{3}\).

Lorsque l’on essaye d’approcher la solution avec les méthodes classiques à un pas, bien sûr lorsque \(N\to+\infty\) on converge vers la solution exacte, cependant en pratique \(N\) est fini et on voit qu’inévitablement nous allons approcher une autre solution que celle correspondant à \(a=1\).

phi = lambda t,y : 3*y/t-5/t**3
    
t0     = 1
tfinal = 5
y0     = 1


def EE(phi,tt,y0):
    h  = tt[1]-tt[0]
    uu = np.zeros(len(tt))
    uu[0] = y0
    for i in range(len(tt)-1):
        uu[i+1] = uu[i]+h*phi(tt[i],uu[i])
    return uu

def EI(phi,tt,y0):
    h  = tt[1]-tt[0]
    uu = np.zeros(len(tt))
    uu[0] = y0
    for i in range(len(tt)-1):
        uu[i+1] = fsolve(lambda x : -x +uu[i]+h*phi(tt[i+1],x),uu[i])[0]
    return uu

def EM(phi,tt,y0):
    h  = tt[1]-tt[0]
    uu = np.zeros(len(tt))
    uu[0] = y0
    for i in range(len(tt)-1):
        utilde = uu[i]+h/2*phi(tt[i],uu[i])
        uu[i+1] = uu[i]+h*phi(tt[i]+h/2,utilde)
    return uu

def CN(phi,tt,y0):
    h  = tt[1]-tt[0]
    uu = np.zeros(len(tt))
    uu[0] = y0
    for i in range(len(tt)-1):
        uu[i+1] = fsolve(lambda x : -x +uu[i]+h/2*(phi(tt[i],uu[i])+phi(tt[i+1],x)),uu[i])[0]
    return uu

def HE(phi,tt,y0):
    h  = tt[1]-tt[0]
    uu = np.zeros(len(tt))
    uu[0] = y0
    for i in range(len(tt)-1):
        utilde = uu[i]+h*phi(tt[i],uu[i])
        uu[i+1] = uu[i] + h/2 * (phi(tt[i],uu[i])+phi(tt[i+1],utilde))
    return uu


NN = [20,100,300,5000]

plt.figure(figsize=(15, 10))

plt.subplot(2,3,1)
for N in NN:
    tt = np.linspace(t0,tfinal,N)
    uu = EE(phi,tt,y0)
    plt.plot(tt,uu,'.-')
plt.plot(tt, sol_exacte(tt,y0),'c-',lw=2)
plt.legend(['N=20','N=100','N=300','N=5000','Exacte'])
plt.title('$y_0=1$ - Exacte vs EE')
plt.axis([t0,tfinal,-c,c]);

plt.subplot(2,3,3)
for N in NN:
    tt = np.linspace(t0,tfinal,N)
    uu = EI(phi,tt,y0)
    plt.plot(tt,uu,'.-')
plt.plot(tt,[sol_exacte(t,y0) for t in tt],'c-',lw=2)
plt.legend(['N=20','N=100','N=300','N=5000','Exacte'])
plt.title('$y_0=1$ - Exacte vs EI')
plt.axis([t0,tfinal,-c,c]);

plt.subplot(2,3,4)
for N in NN:
    tt = np.linspace(t0,tfinal,N)
    uu = EM(phi,tt,y0)
    plt.plot(tt,uu,'.-')
plt.plot(tt,[sol_exacte(t,y0) for t in tt],'c-',lw=2)
plt.legend(['N=20','N=100','N=300','N=5000','Exacte'])
plt.title('$y_0=1$ - Exacte vs EM')
plt.axis([t0,tfinal,-c,c]);

plt.subplot(2,3,5)
for N in NN:
    tt = np.linspace(t0,tfinal,N)
    uu = HE(phi,tt,y0)
    plt.plot(tt,uu,'.-')
plt.plot(tt,[sol_exacte(t,y0) for t in tt],'c-',lw=2)
plt.legend(['N=20','N=100','N=300','N=5000','Exacte'])
plt.title('$y_0=1$ - Exacte vs HE')
plt.axis([t0,tfinal,-c,c]);

plt.subplot(2,3,6)
for N in NN:
    tt = np.linspace(t0,tfinal,N)
    uu = CN(phi,tt,y0)
    plt.plot(tt,uu,'.-')
plt.plot(tt,[sol_exacte(t,y0) for t in tt],'c-',lw=2)
plt.legend(['N=20','N=100','N=300','N=5000','Exacte'])
plt.title('$y_0=1$ - Exacte vs CN')
plt.axis([t0,tfinal,-c,c]);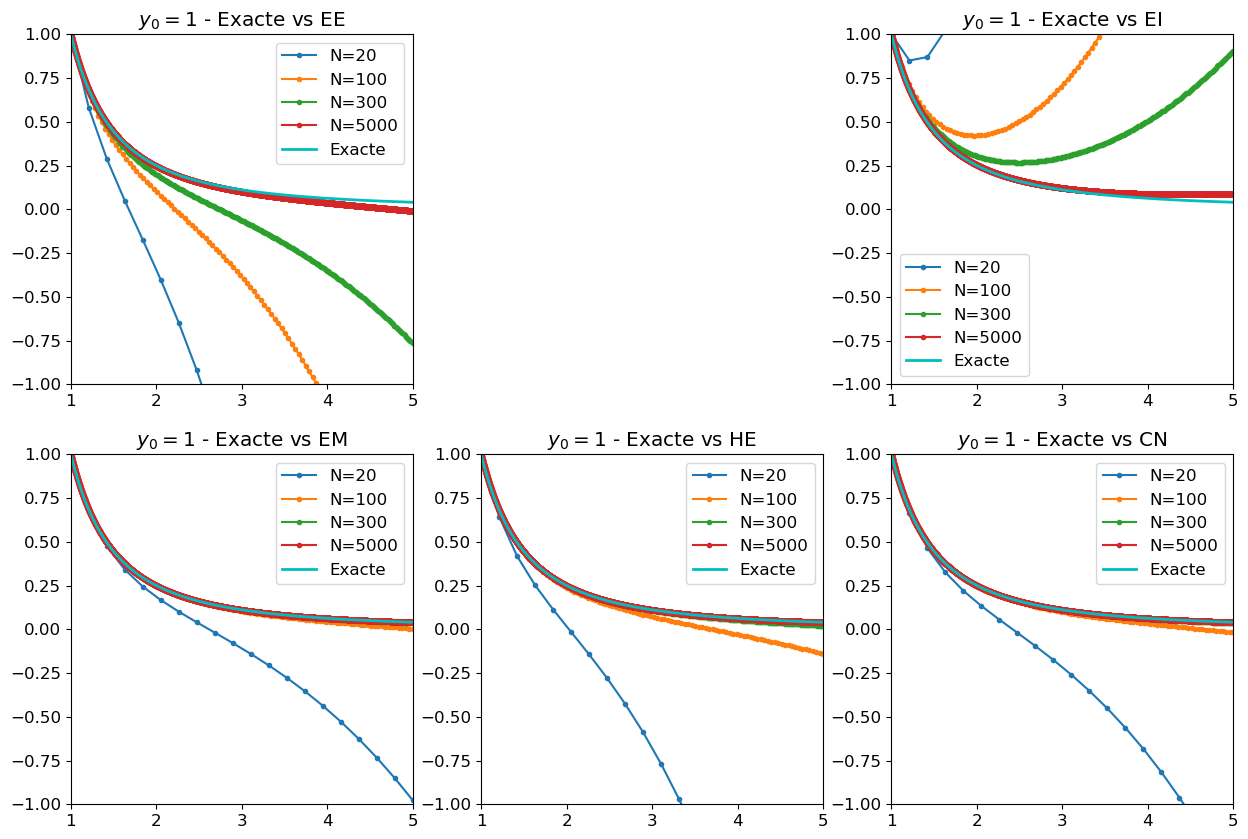

1.3 Problème bien conditionné (= non raide) : solution approchée en un nombre raisonnable d’itérations.

Définition de problème bien conditionné

On dit qu’un problème de Cauchy est bien conditionné si les méthodes numériques usuelles peuvent donner sa solution en un nombre raisonnable d’opérations.

Dans le cas contraire on parle de problème raide.

Exemple de problème MAL conditionné (= raide = stiff)

Considérons le problème de Cauchy avec \(\beta>0\) :

\( \begin{cases} y'(t) = -\beta y(t), &\forall t\in[0;1],\\ y(0) = 1. \end{cases} \)

Ce problème est

• mathématiquement bien posé pour tout \(\beta\in\mathbb{R}\) : il existe une et une seule solution, elle définie sur \(\mathbb{R}\) et est donnée par \(y(t)=e^{-\beta t}\);
• numériquement bien posé pour tout \(\beta>0\) : l’erreur sur la solution sera au pire de l’ordre de l’erreur sur la condition initiale ;
• mal conditionné ou stiff si \(\beta \gg 1\) : plus \(\beta\) est grand, plus le pas \(h\) devient petit car la solution devient de plus en plus raide (stiff) et seul un pas très petit permet d’approcher la solution exacte indépendamment de la méthode numérique utilisée.

Nous allons tracer la solution exacte pour \(\beta=1\), \(\beta=10\), \(\beta=50\) et \(\beta=100\) sur l’intervalle \([0;1]\) pour illustrer ce phénomène.
Nous allons aussi étudier analytiquement le comportement du schéma d’Euler explicite pour ce problème.

Voici ci-dessous le tracé de la solution exacte pour \(\beta\) allant de \(1\) à \(100\) :

exacte = lambda t,b : np.exp(-b*t) 

t0 = 0
tfinal = 1
tt = np.linspace(t0,tfinal,501)

plt.figure(1, figsize=(18, 4))
for i,b in enumerate([1,10,50,100]):
    plt.subplot(1,4,i+1)
    yy = exacte(tt,b) #[exacte(t,b) for t in tt]
    plt.plot(tt, yy)
    plt.title(f'$b={</span>b<span class="sc">}$')
    plt.axis([0,1,0,1])
    plt.grid();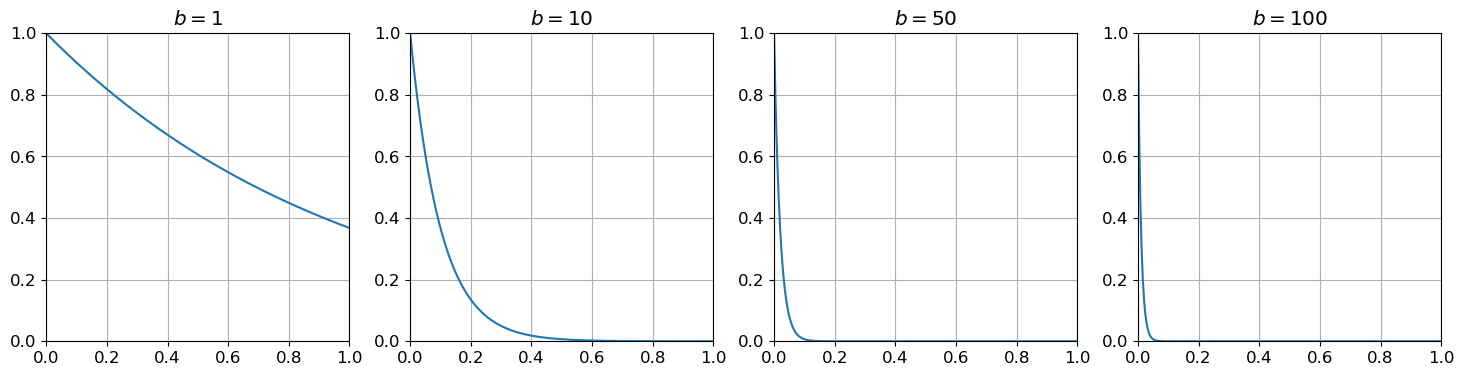

Intuitivement : la solution exacte \(y(t)=e^{-\beta t}\) décroit très rapidement lorsque \(\beta\) est grand ; pour que la solution numérique puisse suivre cette décroissance rapide, il faut qu’il y ait des points dans cette zone de décroissance rapide, c’est-à-dire que le pas \(h\) soit petit.
On verra plus tard que, si on n’est pas intéressé par cette zone de décroit rapide, mais plutôt par le comportement asymptotique de la solution, on peut utiliser des méthodes numériques spécifiques qui permettent de prendre des pas plus grands.

La méthode d’Euler explicite pour cette EDO s’écrit

\( u_{n+1}=(1-\beta h)u_n=\dots=(1-\beta h)^{n+1}u_0. \)

La suite obtenue est une suite géométrique de raison \(q=1-\beta h\). On sait qu’une telle suite

• diverge si \(|q|>1\) ou \(q=-1\),
• est stationnaire si \(q=1\),
• converge vers \(0\) si \(|q|<1\) (de façon monotone vers \(0\) si \(0<q<1\)).

ainsi la solution numérique converge vers \(0\) ssi \(0<\beta h<2\). On voit donc que plus \(\beta\) est grand, plus le pas \(h\) doit être petit pour que la solution numérique puisse approcher la solution exacte. Cela signifie que le problème devient de plus en plus raide (stiff).

Exercie : resolution numérique d’un problème raide

Soient \(b,g>0\) et considérons le problème de Cauchy

\(\begin{cases} y'(t)=-by(t)+g,& t\in[0;1]\\ y(0)=y_0. \end{cases}\)

• Solution exacte

  • Donner l’unique solution exacte à ce problème de Cauchy et tracer le graphe \(t\mapsto y(t)\) pour \(t\ge0\) en fonction de \(y_0\).
    
  • Soient \(b=g=10\). Tracer avec python les solutions exactes sur l’intervalle \([0;1]\) pour \(y_0=\frac{g}{b}\) et \(y(0)=\frac{g}{b}+10^{-8}\) pour \(b=g=10\).
    
  • Sur un graphe à coté tracer les mêmes courbes avec \(b=g=40\). Que peut-on dire lorsque \(b\) devient de plus en plus grand?

• Méthode d’Euler explicite

  • Vérifier que la méthode génère une suite arithmético-géométrique et calculer analytiquement pour quelles valeurs de \(h\) la suite ainsi construite converge et pour quelles valeurs la convergence est monotone.
  • Soient \(b=g=40\) et \(y_0=\frac{g}{b}\). Tracer les solutions approchées obtenues avec \(N=19\), \(N=23\), \(N=45\), \(N=100\).
  • Répéter pour \(y_0=\frac{g}{b}+10^{-8}\) et expliquer chaque résultat.

• Méthode d’Euler implicite

  • Répéter le même exercice pour la méthode d’Euler implicite. Noter que, étant \(\varphi\) linéaire, la méthode peut être rendu explicite par un calcul élémentaire.

Suggestion : EDO y’(t) = ay(t)+b

Considérons l’équation différentielle ordinaire \(y'(t) = ay(t) + b\), où \(a \neq 0\) et \(b\) sont des constantes réelles et considérons une donnée initiale \(y(0) = y_0\neq0\).

On cherche à réécrire cette équation sous la forme d’une équation \(v'(t) = qv(t)\), où \(v\) est une nouvelle fonction à déterminer.

Posons \(v(t) = y(t) + \frac{b}{a}\). Alors \(v(0) = y_0 + \frac{b}{a}\) et

\(\begin{aligned} v'(t) &= y'(t)\\ &= ay(t) + b\\ &=a\left(v(t)-\frac{b}{a}\right)+b\\ &=av(t). \end{aligned}\)

La solution de cette équation est \(v(t) = v(0) e^{at}\).

On conclut alors que \(y(t) = v(t) + \frac{b}{a} = v(0) e^{at} + \frac{b}{a} = \left( y_0 + \frac{b}{a} \right) e^{at} - \frac{b}{a}\), autrement dit

\( \left( y(t)+\frac{b}{a} \right) = \left( y_0+\frac{b}{a} \right) e^{at}. \)

Suggéstion : Suite arithmético-géométrique -> suite géométrique

Une suite \((u_n)\) est dite arithmético-géométrique si elle satisfait une relation de la forme \(u_{n+1}=au_n+b\) avec \(a\neq1\) et \(b\) des réels constants.

On cherche à réécrire cette suite sous la forme d’une suite géométrique \((v_n)\) telle que \(v_{n+1}=qv_n\) avec \(q\) une constante réelle.

On pose \(v_n=u_n-\frac{b}{1-a}\). Alors

\(\begin{aligned} v_{n+1} &= u_{n+1}-\frac{b}{1-a}\\ &=au_n+b-\frac{b}{1-a}\\ &=a\left(v_n+\frac{b}{1-a}\right)+b-\frac{b}{1-a}\\ &=av_n+\frac{ab}{1-a}+b-\frac{b}{1-a}\\ &=av_n+\frac{ab+b(1-a)-b}{1-a}\\ &=av_n. \end{aligned}\)

La suite \((v_n)\) est bien géométrique de raison \(q=a\) donc \(v_n = a^n v_0\).

On conclut alors que \(u_n = a^n v_0 + \frac{b}{1-a}= a^n \left(u_0-\frac{b}{1-a}\right) + \frac{b}{1-a}\), autrement dit

\( \left( u_n-\frac{b}{1-a} \right) = \left( u_0-\frac{b}{1-a} \right) a^n . \)

Correction : solution exacte

Il s’agit de l’edo linéaire d’ordre 1 \(y'(t)=-by(t)+g\), dont la solution est

\( y(t)-\frac{g}{b}=\left( y_0-\frac{g}{b} \right)e^{-bt} \)

et

\( \lim_{t\to+\infty}y(t)=\frac{g}{b} \text{ pour tout } y_0\in\mathbb{R} \)

le problème est numériquement bien posé, c’est-à-dire que l’erreur sur la solution sera au pire de l’ordre de l’erreur sur la condition initiale.

Cependant, lorsque \(b\) devient de plus en plus grand, la solution devient de plus en plus raide:

exacte = lambda t, b, g, y0 : (y0-g/b)*np.exp(-b*t)+g/b 

t0 = 0.
tfinal = 1.0
tt = np.linspace(t0,tfinal,10001)

plt.figure(1, figsize=(15, 5))
plt.subplot(1,2,1)
g = 10
b = 10
Y0 = [g/b, g/b+1.e-8]
for y0 in Y0:
    yy = exacte(tt,b,g,y0) #  [exacte(t,b,g,y0) for t in tt]
    plt.plot(tt,yy,label=('$y_0=$'+str(y0)));
plt.title("$g=b=$"+str(g))
plt.axis([0,1,g/b-1.e-8,g/b+1.e-8])
plt.legend()
plt.grid()

plt.subplot(1,2,2)
g = 40
b = 40
Y0 = [g/b, g/b+1.e-8]
for y0 in Y0:
    yy = exacte(tt,b,g,y0) #  [exacte(t,b,g,y0) for t in tt]
    plt.plot(tt,yy,label=(r'$y_0=$'+str(y0)));
plt.title("$g=b=$"+str(g))
plt.axis([0,1,g/b-1.e-8,g/b+1.e-8])
plt.legend()
plt.grid();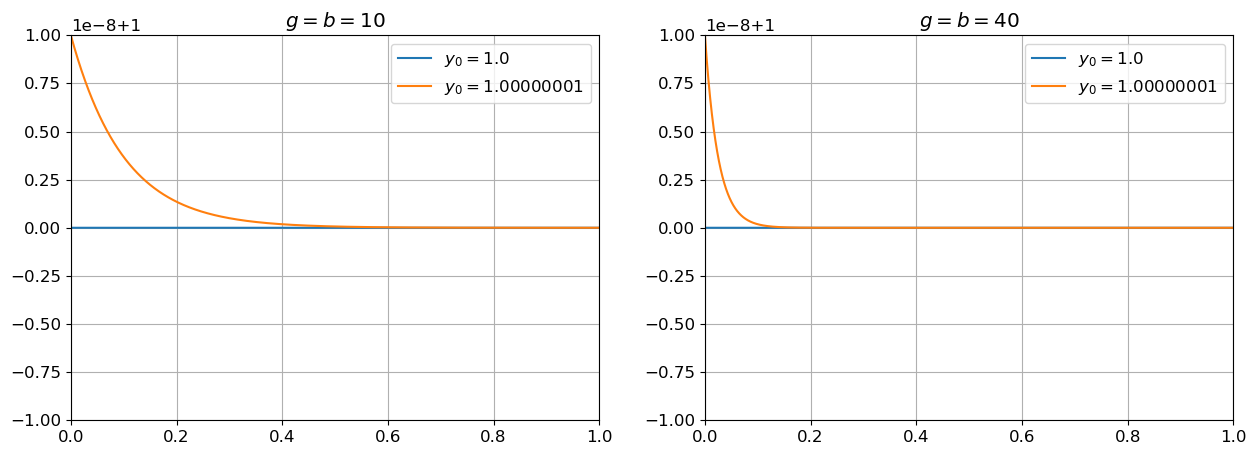

Correction : Méthode d’Euler explicite

La méthode d’Euler explicite donne la suite définie par récurrence \(u_{n+1}=Au_n+B\) avec \(A=1-bh\) et \(B=gh\), soit encore

\( \left( u_n-\frac{B}{1-A} \right) = \left( u_0-\frac{B}{1-A} \right) A^n \quad\leadsto\quad u_n-\frac{g}{b}=(1-hb)^n\left( y_0 -\frac{g}{b}\right). \)

Comparons la solution exacte et la solution approchée :

\(\begin{aligned} y_n&=\frac{g}{b}+\left( y_0 -\frac{g}{b}\right)e^{-bt_n}\\ u_n&=\frac{g}{b}+\left( y_0 -\frac{g}{b}\right)(1-hb)^n \end{aligned}\)

Pour que \(u_n\simeq y_n\) il faut que \((1-hb)^n\simeq e^{-bt_n} \in]0,1]\), donc il faut que \(0\le(1-hb)<1\), soit encore \(h<\frac{1}{b}\). Comme \(h=\frac{T-t_0}{N}=\frac{1}{N}\), cela implique \(N\ge b\). Dans cet exemple, pour obtenir une bonne convergence il est nécessaire de prendre un pas \(h\) de pus en plus petit que \(b\) est grand, c’est-à-dire un coût en calcul plus élevé. On parle de problème raide ou mal conditionné.

phi = lambda t, y, b, g : -b*y+g

def EE(phi,tt,y0,b,g):
    h = tt[1]-tt[0]
    uu = np.zeros_like(tt)
    uu[0] = y0
    for i in range(len(tt)-1):
        uu[i+1] = uu[i]+h*phi(tt[i],uu[i],b,g)
    return uu

t0 = 0.
tfinal = 1.0

g = 40
b = 40
Y0 = [g/b, g/b+1.e-8]
NN = [19, 23, 45, 100]

plt.figure(figsize=(18, 7))
plt.subplot(1,2,1)
y0 = Y0[0]
for N in NN:
    tt = np.linspace(t0,tfinal,N+1)
    yy = EE(phi,tt,y0,b,g)
    plt.plot(tt,yy,label=('$N=$'+str(N)+' noeuds'));
plt.title("Euler explicite, $g=b=$"+str(g)+ ", $y_0$="+str(y0))
plt.axis([0,1,g/b-1.e-8,g/b+1.e-8])
plt.legend()
plt.grid()

plt.subplot(1,2,2)
y0 = Y0[1]
for N in NN:
    tt = np.linspace(t0,tfinal,N+1)
    yy = EE(phi,tt,y0,b,g)
    plt.plot(tt,yy,label=('$N=$'+str(N)+' noeuds'));
plt.title("Euler explicite, $g=b=$"+str(g)+ ", $y_0$="+str(y0))
plt.axis([0,1,g/b-1.e-8,g/b+1.e-8])
plt.legend()
plt.grid()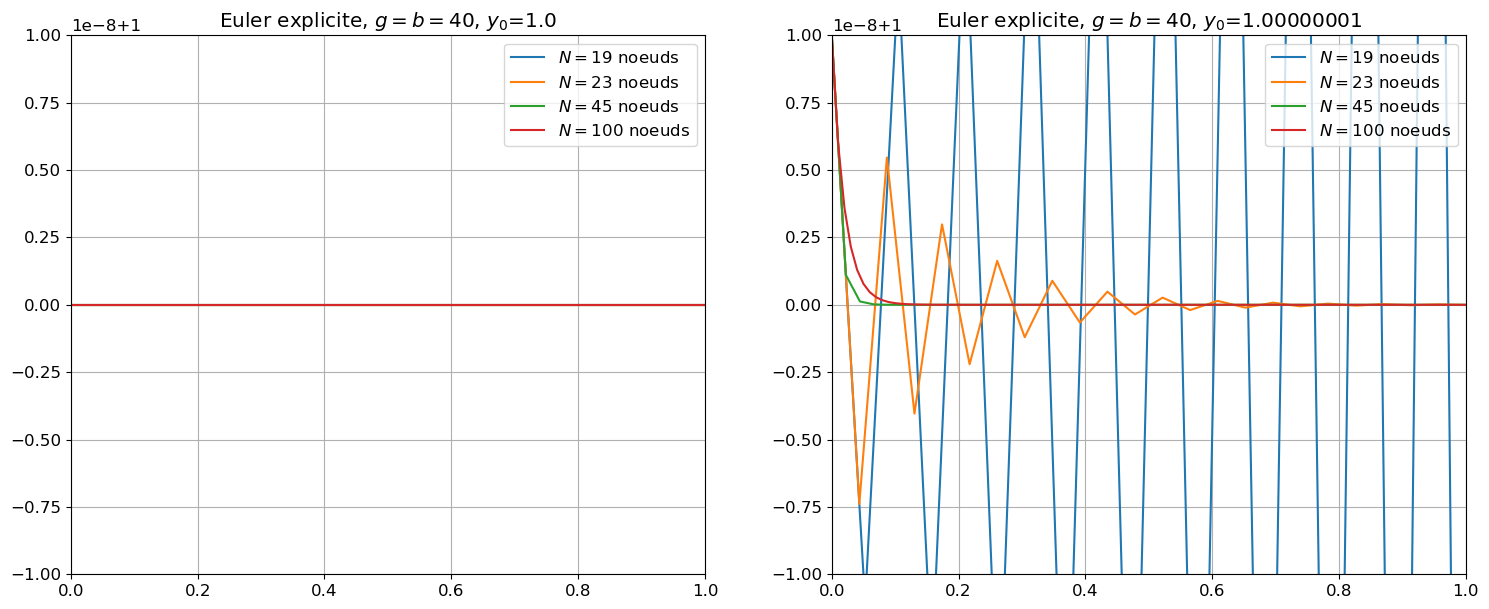

Correction : Méthode d’Euler implicite

La méthode d’Euler implicite donne la suite définie par récurrence \(u_{n+1}=Au_n+B\) avec \(A=\frac{1}{1+bh}\) et \(B=\frac{gh}{1+bh}\), soit encore

\( \left( u_n-\frac{B}{1-A} \right) = \left( u_0-\frac{B}{1-A} \right) A^n \quad\leadsto\quad u_n-\frac{g}{b}=\frac{1}{(1+hb)^n}\left( y_0 -\frac{g}{b}\right). \)

Comparons la solution exacte et la solution approchée :

\(\begin{aligned} y_n&=\frac{g}{b}+\left( y_0 -\frac{g}{b}\right)e^{-bt_n}\\ u_n&=\frac{g}{b}+\left( y_0 -\frac{g}{b}\right)\left(\frac{1}{1+hb}\right)^n \end{aligned}\)

Pour que \(u_n\simeq y_n\) il faut que \(\frac{1}{(1+hb)^n}\simeq e^{-bt_n} \in]0,1]\), donc il faut que \(0\le\frac{1}{1+hb}<1\) c’est-à-dire pour n’importe quelle valeur de \(h\). Dans cet exemple, pour obtenir la convergence il n’est pas nécessaire de limiter le pas \(h\). Cependant, pour une edo quelconque, à chaque pas de temps on doit résoudre une équation non-linéaire.

phi = lambda t,y,b,g : -b*y+g

def EI(phi,tt,y0,b,g):
    h = tt[1]-tt[0]
    uu = np.zeros_like(tt)
    uu[0] = y0
    for i in range(len(tt)-1):
        uu[i+1] = g/b + (y0-g/b)/(1+h*b)**i
        uu[i+1] = fsolve(lambda x: x-uu[i]-h*phi(tt[i+1],x,b,g), uu[i])[0]
    return uu

t0 = 0.
tfinal = 1

g = 40
b = 40
Y0 = [g/b,g/b+1.e-8]
NN = [19, 23, 45, 100]

plt.figure(figsize=(18,7))
plt.subplot(1,2,1)
y0 = Y0[0]
for N in NN:
    tt = np.linspace(t0,tfinal,N+1)
    yy = EI(phi,tt,y0,b,g)
    plt.plot(tt,yy,label=('$N=$'+str(N)+' noeuds'));
plt.title("Euler implicite, $g=b=$"+str(g)+ ", $y_0$="+str(y0))
plt.axis([0,1,g/b-1.e-8,g/b+1.e-8])
plt.legend()
plt.grid()

plt.subplot(1,2,2)
y0 = Y0[1]
for N in NN:
    tt = np.linspace(t0,tfinal,N+1)
    yy = EI(phi,tt,y0,b,g)
    plt.plot(tt,yy,'-*',label=('$N=$'+str(N)+' noeuds'));
plt.title("Euler implicite, $g=b=$"+str(g)+ ", $y_0$="+str(y0))
plt.axis([0,1,g/b-1.e-8,g/b+1.e-8])
plt.legend()
plt.grid()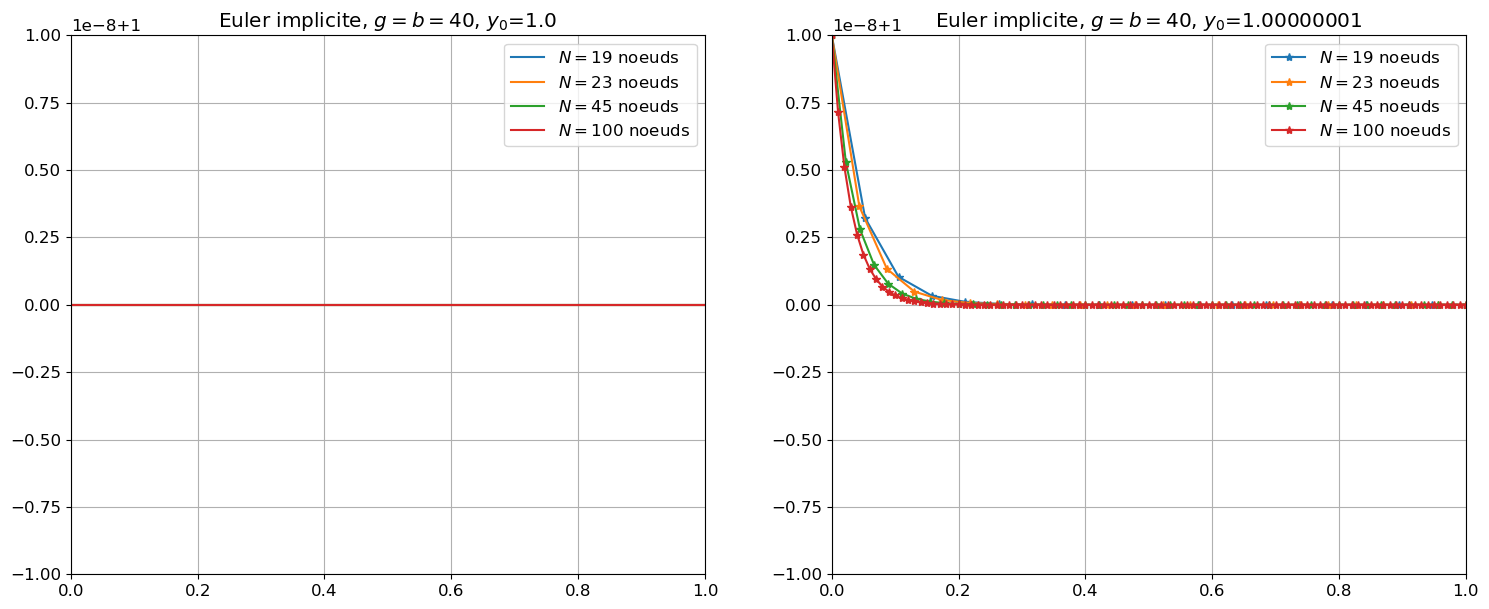

Exercice : problème MAL conditionné

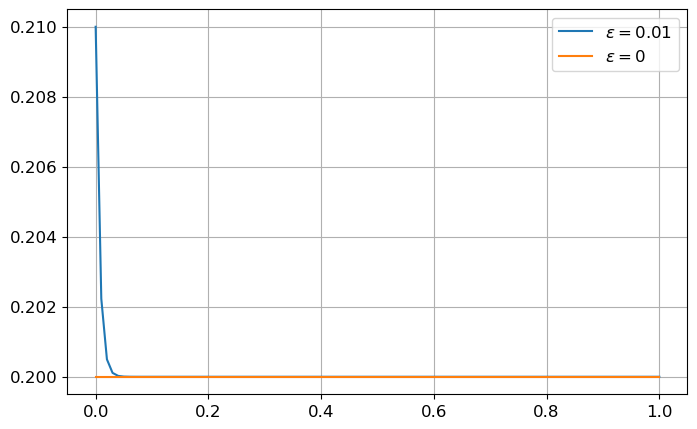
\( \begin{cases} y'(t)=-150y(t)+30\\ y(0)=\frac{1}{5}. \end{cases} \)

Vérifier qu’il est bien posé mathématiquement et numériquement.

Que se passe-t-il si on utilise la méthode d’Euler explicite ?

Le problème de Cauchy donné admet une et une seule solution, la fonction constante \(y(t)=\frac{1}{5}\), il est donc bien posé mathématiquement.

Considérons le problème de Cauchy perturbé

\( \begin{cases} y_\varepsilon'(t)=-150y_\varepsilon(t)+30\\ y_\varepsilon(0)=\frac{1}{5}+\varepsilon. \end{cases} \)

La solution exacte \(y_\varepsilon\) est

\( \left( y_\varepsilon(t)+\frac{30}{-150} \right) = \left( y_\varepsilon(0)+\frac{30}{-150} \right) e^{-150t} \quad\leadsto\quad \left( y_\varepsilon(t)-\frac{1}{5} \right) = \left( y_\varepsilon(0)-\frac{1}{5} \right) e^{-150t} = \varepsilon e^{-150t}. \)

Si \(\varepsilon\to0\), alors \(y_{\varepsilon}(t)\to \frac{1}{5}\) : le problème est numériquement bien posé, car l’erreur sur la solution sera inférieure à l’erreur sur la condition initiale.

# Calcul de la solution exacte
# ============================

t = sym.Symbol('t')
y = sym.Function('y')

edo = sym.Eq( sym.diff(y(t),t) ,  -150*y(t)+30  )
display(edo)
eps = sym.Symbol(r'\varepsilon')
t0, y0 = 0, sym.Rational(1,5)+eps
display(sym.Eq(y(t0),y0))

sol = sym.dsolve(edo,y(t), ics={y(t0):y0})
display(sol)

func = sym.lambdify((t,eps),sol.rhs,'numpy')
tt = np.linspace(0,1,101)
yy_eps = func(tt,0.01)
yy_0 = func(tt,0)
plt.figure(figsize=(8,5))
plt.plot(tt,yy_eps,label=r'$\varepsilon=0.01$')
plt.plot(tt,yy_0,label=r'$\varepsilon=0$')
plt.legend()
plt.grid()

\(\displaystyle \frac{d}{d t} y{\left(t \right)} = 30 - 150 y{\left(t \right)}\)

\(\displaystyle y{\left(0 \right)} = \varepsilon + \frac{1}{5}\)

\(\displaystyle y{\left(t \right)} = \varepsilon e^{- 150 t} + \frac{1}{5}\)

La méthode d’Euler implicite donne la suite définie par récurrence \(u_{n+1} = u_n+h(-150u_{n}+30) = au_n+b\) avec \(a=1-150h\) et \(b=30h\), soit encore

\(\begin{aligned} \left( u_n-\frac{b}{1-a} \right) = \left( u_0-\frac{b}{1-a} \right) a^n &\quad\leadsto\quad \left( u_n-\frac{30h}{150h} \right) = \left( u_0-\frac{30h}{150h} \right) (1-150h)^n \\ &\quad\leadsto\quad \left( u_n-\frac{1}{5} \right) = \left( u_0-\frac{1}{5} \right) (1-150h)^n. \end{aligned}\)

Comparons la solution exacte et la solution approchée :

\(\begin{aligned} y_n-\frac{1}{5} &= \varepsilon e^{-150t}\\ u_n-\frac{1}{5} &= \varepsilon (1-150h)^n \end{aligned}\)

Pour que \(u_n\simeq y_n\) il faut que \((1-150h)^n\simeq e^{-150(nh)} \in]0,1]\), donc il faut que \(|1-150h|<1\), c’est-à-dire \(h<\frac{1}{75}\).

Exercice : problème raide

Il existe des problèmes qui résistent à toutes les méthodes usuelles. On trouve par exemple ces phénomènes en chimie où deux réactions ont des échelles de temps très différentes. Considérons par exemple \( \begin{cases} y'(t)=-1000\big(y(t)-e^{-t}\big)-e^{-t}, & t\in[0;1]\\ y(0)=0. \end{cases} \)

Vérifier, en calculant la solution exacte, que le problème est bien posé mathématiquement et numériquement et qu’il est raide.

# Calcul de la solution exacte
# ============================

t = sym.Symbol('t')
y = sym.Function('y')

edo = sym.Eq( sym.diff(y(t),t) ,  -1000*(y(t)-sym.exp(-t))-sym.exp(-t)  )
display(edo)
eps = sym.Symbol(r'\varepsilon')
t0, y0 = 0, 0+eps
display(sym.Eq(y(t0),y0))

sol = sym.dsolve(edo,y(t), ics={y(t0):y0})
display(sol.expand())

func = sym.lambdify((t,eps),sol.rhs,'numpy')
tt = np.linspace(0,1,501)
yy_1 = func(tt,1)
yy_eps = func(tt,0.01)
yy_0 = func(tt,0)
plt.figure(figsize=(8,5))
plt.plot(tt,yy_1,label=r'$\varepsilon=1$')
plt.plot(tt,yy_eps,'.',label=r'$\varepsilon=0.01$')
plt.plot(tt,yy_0,':',label=r'$\varepsilon=0$')
plt.legend()
plt.grid()

\(\displaystyle \frac{d}{d t} y{\left(t \right)} = - 1000 y{\left(t \right)} + 999 e^{- t}\)

\(\displaystyle y{\left(0 \right)} = \varepsilon\)

\(\displaystyle y{\left(t \right)} = \varepsilon e^{- 1000 t} + e^{- t} - e^{- 1000 t}\)

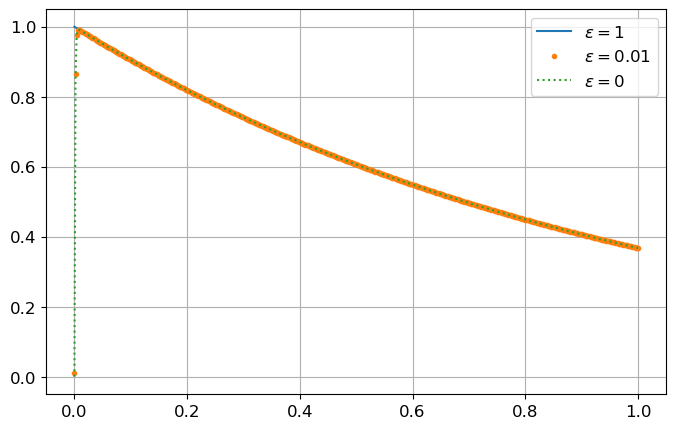
Le problème est

• bien posé mathématiquement : il admet une et une seule solution, la fonction \(y(t)=e^{-t}\), définie sur \(\mathbb{R}\),
• bien posé numériquement : l’erreur \(\varepsilon\) sur la donnée initiale est atténuée au cours du temps,
• raide : la solution exacte \(y(t)=e^{-t}-e^{-1000t}\) croit très rapidement (\(-e^{-1000t}\)) sur un très petit intervalle, puis elle décroit comme \(e^{-t}\). Notons que, si \(\varepsilon=1\), la solution est \(y(t)=e^{-t}\).

PARTIE 1️⃣ Propriétés du problème de Cauchy : que retenir ?

• Un problème de Cauchy est mathématiquement bien posé s’il existe une et une seule solution. Si ce n’est pas le cas, inutile de chercher à approcher la solution numériquement.
• Un problème de Cauchy est numériquement bien posé si la solution d’un problème faiblement perturbé (second membre ou condition initiale) possède une solution proche de celle du problème original. Si ce n’est pas le cas, on peut chercher à approcher la solution numériquement, mais c’est délicat, car une petite erreur peut provoquer une très grande erreur sur la solution. Il faudra alors utiliser des méthodes numériques spécifiques (d’ordre élevé).
• Un problème de Cauchy est bien conditionné si les méthodes numériques usuelles peuvent donner sa solution en un nombre raisonnable d’opérations. Dans le cas contraire on parle de problème raide (stiff). Si un problème est raide, il faudra utiliser des méthodes numériques spécifiques (généralement des méthodes A-stable car on verra que c’est grosso modo le même problème que pour les problèmes numériquement mal posés).

---

2 PARTIE 2️⃣ - propriétés d’un schéma d’approximation : convergence, consistance, stabilité(s)

Rappelons ci-dessous la définition de schéma convergent et de schéma consistant, avant d’introduire la (les) notion(s) de stabilité d’un schéma.

2.1 Convergence et ordre de convergence

Définition: schéma convergent et ordre de convergence

Une méthode numérique est convergente si

\( |y_n-u_n|\le C(h)\xrightarrow[h\to0]{}0 \qquad\forall n=0,\dots,N \)

Si \(C(h) = \mathcal{O}(h^p)\) pour \(p > 0\), on dit que la convergence de la méthode est d’ordre \(p\).

Pour étudier la convergence d’une méthode numérique, on exprime l’erreur \(e_{n+1}\) au pas \(t_{n+1}\) sous la forme :

\(\begin{aligned} e_{n+1} &\equiv y_{n+1} - u_{n+1} \\ &= (y_{n+1} - u_{n+1}^*) + (u_{n+1}^* - u_{n+1}), \\ &=h\tau_{n+1}(h) + (u_{n+1}^* - u_{n+1}), \qquad \tau_{n+1}(h) \equiv \frac{y_{n+1} - u_{n+1}^*}{h} \end{aligned}\)

\(u_{n+1}^*\) désignant la valeur obtenue en appliquant le schéma numérique à la solution exacte au temps \(t_{n+1}\).

• Le terme \(h\tau_{n+1}(h) = y_{n+1} - u_{n+1}^*\) représente l’erreur engendrée par une seule itération du schéma (erreur de consistance).

• Le terme \(u_{n+1}^* - u_{n+1}\) représente la propagation de \(t_{n}\) à \(t_{n+1}\) de l’erreur accumulée au temps précédent \(t_{n}\).

Si les deux termes \((y_{n+1} - u_{n+1}^*)\) et \((u_{n+1}^* - u_{n+1})\) tendent vers zéro lorsque \(h \to 0\), alors la méthode est convergente.

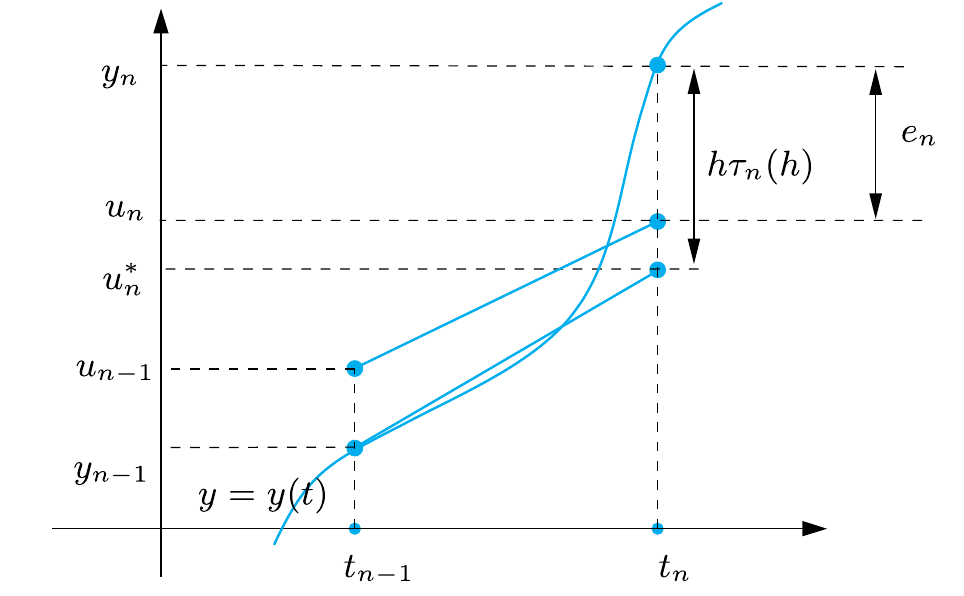
Exemple : convergence de la méthode d’Euler explicite

Considérons le problème de Cauchy \(y'(t)=\varphi(t,y(y))\) pour \(t\in[t_0;T]\) et \(y(t_0)=y_0\). Supposons que la fonction \(\varphi\) soit lipschitzienne de constante \(L\) par rapport à sa deuxième variable. Nous allons montrer que la méthode d’Euler explicite

\( \begin{cases} u_0=y_0,\\ u_{n+1}=u_n+h\varphi(t_n,u_n),&n=0,\dots,N-1 \end{cases} \)

est convergente d’ordre 1.

Pour cela, on étudie séparément l’erreur de consistance et l’accumulation de ces erreurs. On en déduit ensuite la convergence.

Terme \(h\tau_{n+1}(h)=y_{n+1} - u_{n+1}^*\) (erreur de consistance).
Il représente l’erreur engendrée par une seule itération de la méthode d’Euler explicite :

\(\begin{aligned} y_{n+1}-u_{n+1}^* &=y_{n+1}-\Big(y_{n} + h\varphi(t_{n}, y_{n})\Big) \\ &=y(t_{n+1})-y(t_{n}) - h y'(t_n). \end{aligned}\)

En supposant que la dérivée seconde de \(y\) existe et est continue, on sait qu’il existe un point \(\eta_n\) de l’intervalle \(]t_n;t_{n+1}[\) tel que

\( y(t_{n+1})=y(t_n)+hy'(t_n)+\frac{h^2}{2}y''(\eta_n) \)

(développement de Taylor de \(y\) au voisinage de \(t_n\) évalué en \(t_{n+1}\) avec reste de Lagrange). On a alors

\( y_{n+1}-u_{n+1}^* =y(t_{n+1})-y(t_{n}) - h y'(t_n)=\frac{h^2}{2}y''(\eta_n) \le \frac{M}{2}h^2 \xrightarrow[h\to0]{}0 \)

où \(M\equiv\max_{t\in [t_0,T]}|y''(t)|\).

Terme \(u_{n+1}^* - u_{n+1}\) (accumulation des erreurs).
Il représente la propagation de \(t_{n}\) à \(t_{n+1}\) de l’erreur accumulée au temps précédent \(t_{n}\). On a

\(\begin{aligned} u_{n+1}^* - u_{n+1} &= \Big(y_n + h \varphi(t_n, y_n)\Big)-\Big(u_n + h \varphi(t_n, u_n)\Big) \\ &=e_n+h\Big( \varphi(t_n,y_n)-\varphi(t_n,u_n) \Big). \end{aligned}\)

Comme \(\varphi\) est lipschitzienne par rapport à sa deuxième variable, on a

\(|\varphi(t_n,y_n)-\varphi(t_n,u_n)|\le L|y_n-u_n|=L|e_n|.\)

En factorisant on trouve alors

\( |u_{n+1}^{*} - u_{n+1}|\le (1 + hL)|e_{n}|. \)

Convergence.
Comme \(e_0 = 0\), les relations précédentes donnent

\(\begin{aligned} |e_n| & \le |y_n - u_n^*| + |u_n^* - u_n| \\ &\le h|\tau_n(h)| + (1+hL)|e_{n-1}| \\ &\le h|\tau_n(h)| + (1+hL)\left( h|\tau_{n-1}(h)| + (1+hL)|e_{n-2}| \right)| \\ &\le \left( 1+(1+hL)+\dots+(1+hL)^{n-1} \right)h\tau(h) \\ &= \left(\sum_{i=0}^{n-1}(1+hL)^i\right)h\tau(h) \\ &= \frac{(1+hL)^n-1}{hL}h\tau(h) \\ &\le \frac{(e^{hL})^n-1}{hL}h\tau(h) \qquad\text{car }(1+x)\le e^x \\ &= \frac{(e^{hL})^{(t_n-t_0)/h}-1}{L}\tau(h)\qquad\text{car } t_n-t_0=nh \\ &= \frac{e^{L(t_n-t_0)}-1}{L}\tau(h) \\ &= \frac{e^{L(t_n-t_0)}-1}{L}\frac{M}{2}h=\mathcal{O}(h) \end{aligned}\)

On peut conclure que la méthode d’Euler explicite est convergente d’ordre 1.

Remarque : l’estimation de convergence est obtenue en supposant seulement \(\varphi\) lipschitzienne. On peut établir une meilleure estimation si \(\partial_y\varphi\) existe et est non négative pour tout \(t \in [t_0;T]\) et tout \(y\in\mathbb{R}\). En effet dans ce cas \(\begin{align*} u_n^* - u_n &= \left(y_{n-1} + h\varphi(t_{n-1}, y_{n-1})\right) - \left( u_{n-1} + h\varphi(t_{n-1},u_{n-1})\right) \\ &= e_{n-1}+h\left( \varphi(t_{n-1},y_{n-1})-\varphi(t_{n-1},u_{n-1}) \right) \\ &= e_{n-1}+h\left( e_{n-1}\partial_y\varphi(t_{n-1},\eta_n) \right) \\ &= \left( 1+h\partial_y\varphi(t_{n-1},\eta_n) \right)e_{n-1} \end{align*}\) où \(\eta_n\) appartient à l’intervalle dont les extrémités sont \(y_{n-1}\) et \(u_{n-1}\). Ainsi, si \( 0<h<\frac{2}{\max\limits_{t\in[t_0,T]}\partial_y\varphi(t,y(t))} \) alors \( |u_n^* - u_n |\le |e_{n-1}|. \) On en déduit \(|e_n| \le |y_n - u_n^*| + |e_{n-1}| \le nh\tau(h) + |e_0|\) et donc \( |e_n|\le M \frac{h}{2}(t_n-t_0). \) La restriction sur le pas de discrétisation \(h\) est une condition de stabilité, comme on le verra dans la suite.

Théorème d’équivalence de Lax-Ritchmyer : consistance + zéro-stabilité = convergence

Un schéma consistant est convergent ssi il est zéro-stable.

2.2 Consistance et ordre de consistance

Définition : erreurs de troncature

L’erreur de troncature locale est donnée par :

\( \tau_{n+1}(h) \equiv \frac{y_{n+1} - u_{n+1}^*}{h}. \)

Elle représente (à un facteur \(1/h\) près) l’erreur introduite en insérant la solution exacte dans le schéma numérique.

L’erreur de troncature globale (ou simplement erreur de troncature) est définie comme :

\( \tau(h) = \max_{n=0,\dots,N} |\tau_n(h)|. \)

Elle correspond à la borne supérieure de l’erreur de troncature locale sur l’ensemble des pas de temps.

Définition : Consistance et ordre de consistance

• Une méthode numérique est dite consistante si \(\lim_{h\to0} \tau(h) = 0\).
  
• Elle est consistante d’ordre \(p\) si l’erreur de troncature vérifie \(\tau(h) = \mathcal{O}(h^p)\), pour un certain \(p \geq 1\).

Remarque : La propriété de consistance est une condition nécessaire pour la convergence. En effet, sans consistance, la méthode introduirait à chaque itération une erreur qui ne tendrait pas vers zéro lorsque \(h\) diminue. L’accumulation de ces erreurs empêcherait alors l’erreur globale de s’annuler lorsque \(h \to 0\).

Remarque : l’ordre de convergence coïncide en général avec l’ordre de son erreur de troncature.

2.3 Deux notions de stabilité : zéro-stabilité et A-stabilité

De manière générale, un schéma numérique est considéré comme stable s’il permet de maîtriser la solution lorsqu’on perturbe les données. Il existe plusieurs notions de stabilité, nous allons en détailler deux : la zéro-stabilité et l’A-stabilité.

Prenons le problème de Cauchy, supposé mathématiquement et numériquement bien posé :

\( \begin{cases} y'(t) = \varphi(t,y(t)), &\forall t \in I=]t_0,T[,\\ y(t_0) = y_0. \end{cases} \)

Deux questions naturelles se posent alors :

• Que se passe-t-il lorsque l’on fixe le temps final \(T\) et que l’on fait tendre le pas \(h\) vers \(0\) ?
  
• Que se passe-t-il lorsque l’on fixe le pas \(h>0\) et que l’on fait tendre \(T\) vers l’infini ?

Dans ces deux cas, le nombre de nœuds tend vers l’infini, mais les enjeux diffèrent : dans le premier cas, on s’intéresse à l’erreur en chaque point, tandis que dans le second, il s’agit du comportement asymptotique de la solution approchée.

Ces deux problématiques font intervenir deux notions de stabilité :

• Zéro-stabilité
  Elle concerne la résolution du problème de Cauchy sur des intervalles bornés (le nombre \(N\) de sous-intervalles ne tend vers l’infini que lorsque \(h\) tend vers zéro).
  Elle garantit que la méthode numérique est peu sensible aux petites perturbations des données. Si la méthode numérique n’est pas zéro-stable, les erreurs d’arrondi sur \(y_0\) et le calcul de \(\varphi(t_n,y_n)\) rendent la solution calculée inutilisable.

• A-stabilité
  Dans certaines situations, le problème de Cauchy doit être résolu sur des intervalles de temps très longs, voire infinis. Ici, même pour un \(h\) fixé, le nombre \(N\) de sous-intervalles tend vers l’infini. On recherche alors des méthodes capables d’approcher la solution sur des intervalles de temps arbitrairement grands.
  Idéalement, on souhaiterait utiliser des pas de temps \(h\) suffisamment grands (une méthode est dite inconditionnellement A-stable si l’on peut choisir \(h>0\) sans restriction ; sinon, une condition de stabilité sur \(h\) déterminera le temps de calcul).

2.3.1 Étude de la zéro-stabilité (dans \(\mathbb{R}\)) pour les schémas à un pas

La zéro-stabilité garantit que, sur un intervalle borné, de petites perturbations des données entraînent des perturbations contrôlées de la solution numérique lorsque \(h\to0\).

Plus précisément, une méthode numérique visant à approcher le problème de Cauchy sur un intervalle fini \(I=[t_0,T]\) est dite zéro-stable si les conditions suivantes sont satisfaites :

\( \exists h_0>0,\ \exists C>0,\ \exists \varepsilon_0>0\ \text{tels que}\ \forall h\in]0,h_0],\ \forall \varepsilon\in]0,\varepsilon_0],\ \text{si } |\varrho_n| \le \varepsilon,\ 0 \le n \le N, \)

alors

\( |z_n - u_n| \le C\varepsilon,\ 0 \le n \le N \)

où : - \(C\) est une constante indépendante de \(h\), - \(u_n\) est la solution obtenue par le schéma numérique sans perturbation, - \(z_n\) est la solution obtenue par le même schéma appliqué au problème perturbé, - \(\varrho_n\) représente la perturbation au \(n\)-ième pas, - \(\varepsilon_0\) est la perturbation maximale admissible.

Il est important de noter que \(\varepsilon_0\) doit être suffisamment petit pour que le problème perturbé conserve une solution unique sur l’intervalle d’intégration considéré.

Dans le cas d’une méthode consistante à un pas, on peut démontrer que la zéro-stabilité découle du fait que \(\varphi\) est lipschitzienne par rapport à sa seconde variable. Dans ce contexte, la constante \(C\) dépend de \(\exp((T-t_0)L)\), où \(L\) est la constante de Lipschitz. Toutefois, cette propriété n’est pas nécessairement vérifiée pour d’autres familles de méthodes numériques.

Exemple : zéro-stabilité de la méthode d’Euler explicite

Considérons \(u_n\) comme l’approximation obtenue avec la méthode d’Euler explicite pour le problème initial :

\( \begin{cases} u_0 = y_0, \\ u_{n+1} = u_n + h\varphi(t_n, u_n), & n = 0, \dots, N - 1 \end{cases} \)

et \(z_n\) comme l’approximation obtenue avec la méthode d’Euler explicite pour le problème perturbé :

\( \begin{cases} z_0 = y_0 + \varrho_0, \\ z_{n+1} = z_n + h\left(\varphi(t_n, z_n) + \varrho_n\right), & n = 0, \dots, N - 1 \end{cases} \)

Nous avons alors :

\(\begin{align} |u_n - z_n| &\le |u_{n-1} - z_{n-1}| + h|\varphi(t_{n-1}, u_{n-1}) - \varphi(t_{n-1}, z_{n-1})| + h|\varrho_n| \\ &\le (1 + hL)|u_{n-1} - z_{n-1}| + h\varepsilon \\ &\le (1 + hL)^2|u_{n-2} - z_{n-2}| + (1 + (1 + hL))h\varepsilon \\ &\vdots \\ &\le (1 + hL)^n|\varrho_0| + \left(1 + (1 + hL) + \dots + (1 + hL)^{n-1}\right)h\varepsilon \\ &= (1 + hL)^n|\varrho_0| + \left(\sum_{i=0}^{n-1}(1 + hL)^i\right)h\varepsilon \\ &= (1 + hL)^n|\varrho_0| + \frac{(1 + hL)^n - 1}{L}\varepsilon \\ &\le (e^{hL})^n|\varrho_0| + \frac{(e^{hL})^n - 1}{hL}h\varepsilon \qquad\text{car } (1 + x) \le e^x \\ &= e^{nhL}|\varrho_0| + \frac{e^{nhL} - 1}{L}\varepsilon \\ &\le \left(e^{nhL} + \frac{e^{nhL} - 1}{L}\right)\varepsilon \\ &= \frac{(1 + L)e^{L(T - t_0)} - 1}{L}\varepsilon \qquad\text{car } t_n - t_0 = nh \end{align}\)

Ainsi, nous avons montré que la méthode d’Euler explicite est zéro-stable.

2.3.2 Étude de la A-stabilité (dans \(\mathbb{R}\)) pour les schémas à un pas

Dans la section précédente, nous avons étudié la résolution du problème de Cauchy sur des intervalles bornés. Dans ce contexte, le nombre \(N\) de sous-intervalles ne tend vers l’infini que lorsque \(h\) tend vers zéro.
Cependant, il existe de nombreuses situations où le problème de Cauchy doit être résolu sur des intervalles de temps très longs, voire infinis. Dans ces cas-là, même pour un \(h\) fixé, \(N\) tend vers l’infini, rendant la notion de zéro-stabilité inapplicable puisque \(T - t_0 \to +\infty\).
On cherche donc des méthodes capables d’approcher la solution sur des intervalles de temps arbitrairement grands, y compris avec des pas de temps \(h\) relativement grands.

Définition : A-stabilité dans \(\mathbb{R}\)

Soit \(\beta > 0\) un réel positif et considérons le problème de Cauchy (modèle simplifié = toy-model) :

\(\begin{cases} y'(t) = -\beta y(t), &\text{pour } t > 0, \\ y(0) = y_0 \end{cases}\)

où \(y_0 \neq 0\) est une valeur initiale donnée. La solution exacte est \(y(t) = y_0 e^{-\beta t}\), d’où :

\(\lim_{t \to +\infty} y(t) = 0.\)

Considérons un pas de temps fixé \(h > 0\) et définissons \(t_n = nh\) pour \(n \in \mathbb{N}\). Notons \(u_n \approx y(t_n)\) une approximation de la solution \(y\) au temps \(t_n\).
Si, sous d’éventuelles conditions sur \(h\), on a

\( \lim_{n \to +\infty} u_n = 0, \)

alors on dit que le schéma est A-stable.

Remarques :

• Des conclusions similaires restent valables lorsque \(\beta\) est un nombre complexe ou une fonction positive de \(t\) (ce cas sera traité dans la section suivante).
  
• À première vue, l’exigence d’une stabilité absolue pour une méthode numérique appliquée à un autre problème que le toy-model peut sembler superflue. Cependant, il est possible de démontrer que si une méthode est absolument stable pour le toy-model, alors, lorsqu’elle est appliquée à un problème plus général, l’erreur de perturbation (c’est-à-dire la différence absolue entre la solution perturbée et la solution non perturbée) reste uniformément bornée par rapport à \(h\).
  En d’autres termes, une méthode absolument stable selon la définition appliquée au toy-model garantit un contrôle des perturbations même dans des contextes plus généraux.

2.3.2.1 A-stabilité d’un système et problèmes raides

Cette définition peut être généralisée à un système de \(n\) EDO de la forme

\( \mathbf{y}'(t) = -\mathbb{A}\mathbf{y}(t) \)

où \(\mathbb{A}\) est une matrice constante ayant \(n\) valeurs propres positives \(\lambda_i\), \(i = 1, 2, \dots, n\).
La solution s’écrit

\( \mathbf{y}(t) = \sum_i c_i \mathbf{v}_i e^{-\lambda_i t} \)

où \(\mathbf{v}_i\) est le \(i\)-ème vecteur propre associé à la valeur propre \(\lambda_i\). On a donc :

\( \lim_{t \to +\infty} y_i(t) = 0 \quad \forall i = 1, 2, \dots, n. \)

Systèmes raides (stiff systems) : un système d’équations différentielles est dit raide lorsque les valeurs propres \(\lambda_i\) de la matrice \(\mathbb{A}\) présentent des magnitudes très différentes. En d’autres termes, si certaines valeurs propres sont beaucoup plus grandes que d’autres, alors le système évolue selon des échelles de temps très variées. Cette différence de magnitudes crée un défi pour les méthodes numériques : pour garantir la A-stabilité, il est parfois nécessaire de choisir un pas de temps \(h\) suffisamment petit, proportionnel au plus grand \(\lambda_i\). Cela peut rendre les calculs très coûteux lorsque les valeurs propres sont très disparates. En revanche, les méthodes inconditionnellement A-stables sont préférées pour les systèmes raides, car elles permettent d’utiliser des pas de temps plus grands tout en maintenant la A-stabilité, indépendamment du plus grand \(\lambda_i\).

2.3.2.2 Exemples et exercices sur la A-stabilité

Exemple : étude de l’A-stabilité du schéma d’Euler explicite

Le schéma d’Euler progressif appliqué au toy-model (\(\varphi(t,y)=-\beta y\)) s’écrit

\( u_{n+1}=(1-\beta h)u_n, \qquad n=0,1,2,\dots \)

et par suite

\( u_{n}=(1-\beta h)^nu_0, \qquad n=0,1,2,\dots \)

Par conséquente, \(\lim\limits_{n\to+\infty}u_n=0\) si et seulement si

\( \left|1-\beta h\right|<1, \)

ce qui a pour effet de limiter \(h\) à

\( \boxed{h<\frac{2}{\beta}.} \)

Cette condition de A-stabilité limite le pas \(h\) d’avance en \(t\) lorsqu’on utilise le schéma d’Euler progressif.

Remarques :

• Cette convergence est monotone ssi \(1-\beta h>0\), i.e. ssi \(h<\frac{1}{\beta}\) (bien plus restrictif que la condition de A-stabilité).
• Notons que si \(1-\beta h>1\) alors \(u_n\) tend vers \(+\infty\) lorsque \(t\) tend vers l’infini et si \(1-\beta h<-1\) alors \(u_n\) tend vers l’infini en alternant de signe lorsque \(t\) tend vers l’infini. Nous dirons dans ces cas que le schéma d’Euler progressif est instable.
• Dans le cas du système, le schéma d’Euler progressif est A-stable ssi \(h<\frac{2}{\lambda_\text{max}}\).

Exercice : étudier l’A-stabilité du schéma d’Euler implicite

\( \begin{cases} u_0 = y_0,\\ u_{n+1} = u_{n}+h \varphi_{n+1}, & n=0,1,\dots,N-1. \end{cases} \)

Le schéma d’Euler rétrograde devient dans le cadre de notre exemple \( (1+\beta h)u_{n+1}=u_n, \qquad n=0,1,2,\dots \) et par suite \( u_{n}=\frac{1}{(1+\beta h)^{n}}u_0, \qquad n=0,1,2,\dots \) Dans ce cas nous voyons que pour tout \(h>0\) nous avons \(\lim_{n\to\infty}u_n=0\), le schéma d’Euler rétrograde est donc toujours stable, sans limitations sur \(h\).

Exercice : étudier l’A-stabilité du schéma d’Euler modifié

\( \begin{cases} u_0 = y_0,\\ u_{n+1} = u_{n}+h \varphi\left(t_n+\frac{h}{2},u_n+\frac{h}{2}\varphi_n\right), & n=0,1,\dots,N-1. \end{cases} \)

Le schéma d’Euler modifié pour notre exemple devient \( u_{n+1}=u_n+h\left( -\beta\left( u_n+\frac{h}{2}(-\beta u_n) \right) \right) =\left(1-\beta h +\frac{(\beta h )^2}{2} \right) u_{n} \) Par induction on obtient \( u_{n}=\left(1-\beta h +\frac{(\beta h )^2}{2} \right)^nu_0. \) Par conséquent, \(\lim\limits_{n\to+\infty}u_n=0\) si et seulement si \( \left| 1 - \beta h +\frac{1}{2}(\beta h)^2 \right|<1. \) Notons \(x\) le produit \(\beta h\) et \(q\) le polynôme \(q(x)=\frac{1}{2}x^2-x+1\) dont le graphe est représenté en figure:

xx = np.linspace(0,3,101)
yy = 1-xx+0.5*xx**2
plt.plot(xx,yy,[0,2,2],[1,1,0],'m:')
plt.axis([0,3,0,3])
plt.xlabel(r'$h\beta$')
plt.ylabel(r'$q(h\beta)$');

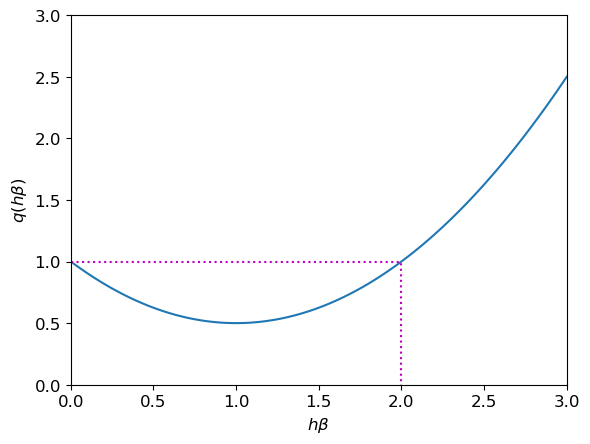
Nous avons \(|q(x)|<1\) si et seulement si \(0<x<2\). La relation \(\lim\limits_{n\to+\infty}u_n=0\) est donc satisfaite si et seulement si \( \boxed{ h <\frac{2}{\beta}. } \) Cette condition de stabilité limite le pas \(h\) d’avance en \(t\) lorsqu’on utilise le schéma d’Euler modifié.

Notons qu’on a la même condition de A-stabilité que le schéma d’Euler explicite. Cependant, \(q(x)>0\) pour tout \(x\), donc cette convergence est monotone (tandis qu’avec le schéma d’Euler explicite la convergence n’est monotone que si \(h<\frac{1}{\beta}\)).

Exercice : étudier l’A-stabilité du schéma de Cranck-Nicolson

\( \begin{cases} u_0 = y_0,\\ u_{n+1} = u_{n}+\frac{h}{2}\left(\varphi_n+\varphi_{n+1}\right), & n=0,1,\dots,N-1. \end{cases} \)

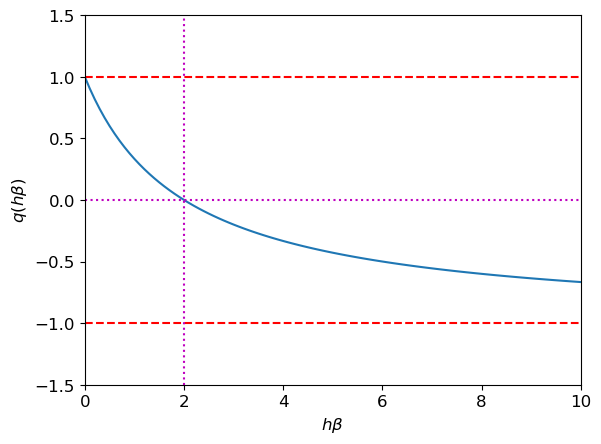
Le schéma de Crank-Nicolson appliqué à notre exemple s’écrit \( \left(1+\frac{\beta h}{2}\right)u_{n+1} = \left(1-\frac{\beta h}{2}\right) u_{n} \) et par suite \( u_{n}=\left( \frac{2-\beta h}{2+\beta h} \right)^{n}u_0, \qquad n=0,1,2,\dots \) Par conséquent, \(\lim\limits_{n\to+\infty}u_n=0\) si et seulement si \( \left|\frac{2-\beta h}{2+\beta h}\right|<1. \) Notons \(x\) le produit \(\beta h>0\) et \(q\) la fonction \(q(x)=\frac{2-x}{2+x}=1-2\frac{x}{2+x}\). Nous avons \(0<\frac{x}{2+x}<1\) pour tout \(x\in\mathbb{R}_+^*\), donc \(|q(x)|<1\) pour tout \(x\in\mathbb{R}_+^*\). La relation \(\lim\limits_{n\to+\infty}u_n=0\) est donc satisfaite pour tout \(h>0\): le schéma de Crank-Nicolson est donc toujours stable, sans limitations sur \(h\).
Cependant, si on cherche \(0<q<1\) on a (pour \(x>0\)) \( 1-2\frac{x}{2+x}>0 \iff x<2. \)

xx = np.linspace(0,10,101)
yy = 1-2*xx/(2+xx)
plt.plot(xx,yy)
plt.plot([0,10],[1,1],'r--',[0,10],[-1,-1],'r--')
plt.plot([0,10],[0,0],'m:',[2,2],[-1.5,1.5],'m:')
plt.axis([0,10,-1.5,1.5])
plt.xlabel(r'$h\beta$')
plt.ylabel(r'$q(h\beta)$');

Exercice : étudier l’A-stabilité du schéma de Heun

Le schéma de Heun pour notre exemple devient \( u_{n+1} =u_n+\frac{h}{2}\left( -\beta u_n-\beta\left( u_n+h(-\beta u_n) \right) \right) =\left(1-\beta h +\frac{(\beta h )^2}{2} \right) u_{n} \) ce qui coïncide avec la méthode d’Euler modifiée. Par conséquent, \(\lim\limits_{n\to+\infty}u_n=0\) si et seulement si \( \boxed{ h <\frac{2}{\beta} } \) et cette convergence est monotone.
Cette condition de stabilité limite le pas \(h\) d’avance en \(t\) lorsqu’on utilise le schéma de Heun.

Exercice : étudier l’A-stabilité du schéma de Simpson implicite

Le schéma de Simpson implicite appliqué à notre exemple s’écrit \( \left(1+\beta\frac{h}{6}\right)u_{n+1} = \left(1-\frac{5}{6}\beta h+\frac{1}{3}(\beta h)^2\right) u_{n} \) et par suite \( u_{n}=\left( \frac{ 1-\frac{5}{6}\beta h+\frac{1}{3}(\beta h)^2 }{ 1+\beta\frac{h}{6} } \right)^{n}u_0, \qquad n=0,1,2,\dots \) Par conséquent, \(\lim\limits_{n\to+\infty}u_n=0\) si et seulement si \( \left|\frac{ 6-5\beta h+2(\beta h)^2 }{ 6+\beta h }\right|<1. \) Notons \(x\) le produit \(\beta h>0\) et \(q\) la fonction \(q(x)=\frac{6-5x+2x^2}{6+x}\) dont le graphe est représenté en figure.

xx = np.linspace(0,4,101)
yy = (6-5*xx+2*xx**2)/(6+xx)
plt.plot(xx,yy,[0,3,3],[1,1,0],'m:')
plt.axis([0,4,0,3])
plt.xlabel(r'$h\beta$')
plt.ylabel(r'$q(h\beta)$');

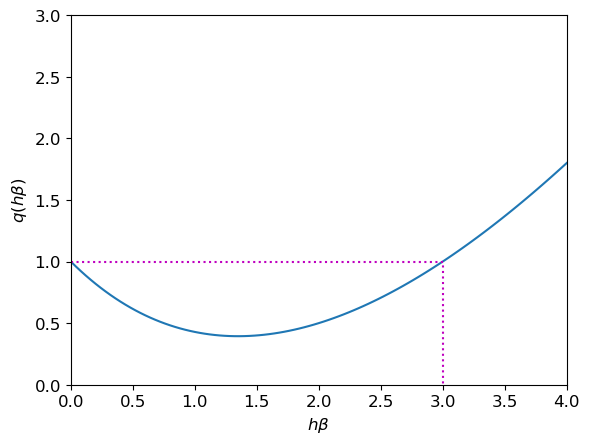
Nous avons \(q(x)>0\) pour tout \(x\in\mathbb{R}_+^*\) et \(q(x)<1\) si et seulement si \(x<3\), donc \(|q(x)|<1\) pour tout \(x\in]0;3[\). Par conséquent, \(\lim\limits_{n\to+\infty}u_n=0\) si et seulement si \( h <\frac{3}{\beta}. \) Cette condition de stabilité limite le pas \(h\) d’avance en \(t\).

Exercice : étudier l’A-stabilité du schéma de Simpson explicite

Le schéma de Simpson explicite pour notre exemple devient \( u_{n+1} = u_n+\frac{h}{6}\left( -\beta u_n -4 \beta\left( u_n+\frac{h}{2}(-\beta u_n) \right) -\beta\left( u_n+h(-\beta u_n) \right) \right) =\left(1-\beta h +\frac{3}{2}(\beta h )^2 \right) u_{n} \) Par induction on obtient \( u_{n}=\left(1-\beta h +\frac{3}{2}(\beta h )^2 \right)^nu_0. \) Par conséquent, \(\lim\limits_{n\to+\infty}u_n=0\) si et seulement si \( \left|1-\beta h +\frac{3}{2}(\beta h )^2\right|<1. \) Notons \(x\) le produit \(\beta h\) et \(q\) le polynôme \(q(x)=\frac{3}{2}x^2-x+1\) dont le graphe est représenté en figure.

xx = np.linspace(0,3,101)
yy = 1-xx+1.5*xx**2
plt.plot(xx,yy,[0,2/3,2/3],[1,1,0],'m:')
plt.axis([0,3,0,3])
plt.xlabel(r'$h\beta$')
plt.ylabel(r'$q(h\beta)$');

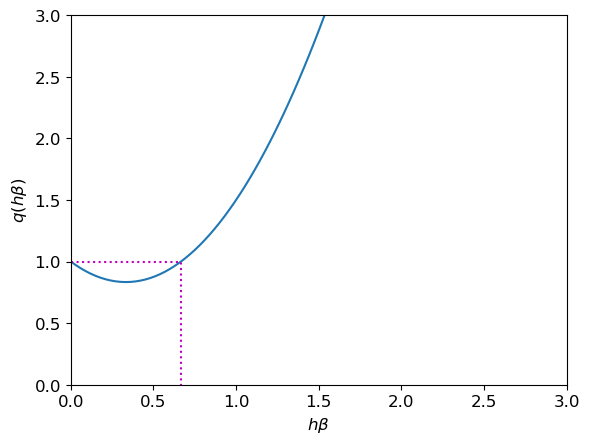
Nous avons \(|q(x)|<1\) si et seulement si \(0<x<\frac{2}{3}\). La relation \(\lim\limits_{n\to+\infty}u_n=0\) est donc satisfaite si et seulement si \( h <\frac{2}{3\beta}. \) Cette condition de stabilité limite le pas \(h\) d’avance en \(t\).

2.4 Tableau récapitulatif, implémentation des schémas et tests

\( \begin{array}{|c|c|c|c|c|c|} \hline \text{Acronyme} & \text{Schéma} & \text{Type} & \text{Ordre} & \text{A-stabilité} & \text{Positivité} \\ \hline \text{EE} & u_{n+1} = u_n + h\varphi_n & \text{Explicite} & 1 & 0 < h < \frac{2}{\beta} & 0 < h < \frac{1}{\beta} \\ \text{EI} & u_{n+1} = u_n + h\varphi_{n+1} & \text{Implicite} & 1 & \forall h > 0 & \forall h > 0 \\ \text{EM} & u_{n+1} = u_n + h\varphi\left(t_n + \frac{h}{2}, u_n + \frac{h}{2}\varphi_n\right) & \text{Explicite} & 2 & 0 < h < \frac{2}{\beta} & 0 < h < \frac{2}{\beta} \\ \text{CN} & u_{n+1} = u_n + \frac{h}{2}\left(\varphi_n + \varphi_{n+1}\right) & \text{Implicite} & 2 & \forall h > 0 & 0 < h < \frac{2}{\beta} \\ \text{H} & u_{n+1} = u_n + \frac{h}{2}\left(\varphi_n + \varphi(t_{n+1}, u_n + h\varphi_n)\right) & \text{Explicite} & 2 & 0 < h < \frac{2}{\beta} & 0 < h < \frac{2}{\beta} \\ \hline \end{array} \)

Exercice : tester numériquement l’A-stabilité des schémas classiques à un pas

On considère le toy-model avec \(\beta=1\) et on teste numériquement l’A-stabilité des schémas d’Euler explicite, d’Euler implicite, d’Euler modifié, de Crank-Nicolson et de Heun.

\( \begin{cases} y'(t)=-y(t), & t\in[0;12]\\ y(0)=1. \end{cases}\)

Calculer la solution exacte. Calculer ensuite la solution approchée par les schémas pour différentes valeurs de \(h\). Vérifier que les conditions de stabilité sont respectées.

Solution exacte

L’unique solution du problème de Cauchy est la fonction \(y(t)=e^{-t}\) définie pour tout \(t\) \(\in\) \(\mathbb{R}\).

phi = lambda t,y : -y
sol_exacte = lambda t : np.exp(-t)

# INITIALISATION
t0, y0, tfinal = 0 , 1 , 12

# PREPARATIONS DES CAS TEST pour différentes valeurs de h
H = [ 2**(k-2) for k in range(5) ]
T = [ np.arange(t0,tfinal,h) for h in H] # liste des grilles

yy = sol_exacte(T[0]) # on affichera la sol exacte sur la grille la plus fine

Solution approchée par la méthode d’Euler explicite

La méthode d’Euler explicite pour cette EDO s’écrit

\( u_{n+1}=(1-h)u_n. \)

En procédant par récurrence sur \(n\), on obtient

\( u_{n+1}=(1-h)^{n+1}. \)

De la formule \(u_{n+1}=(1-h)^{n+1}\) on déduit que

• si \(0<h<1\) alors la solution numérique est stable et convergente,
• si \(h=1\) alors la solution numérique est stationnaire \(u_n=0\) pour tout \(n\in\mathbb{N}^*\),
• si \(1<h<2\) alors la solution numérique oscille mais est encore convergente,
• si \(h=2\) alors la solution numérique oscille, plus précisément on a \(u_{2n}=1\) et \(u_{2n+1}=-1\) pour tout \(n\in\mathbb{N}^*\),
• si \(h>2\) alors la solution numérique oscille et diverge.

En effet, la méthode est A-stable si et seulement si \(|1 - h| < 1\).

Remarque : la suite obtenue est une suite géométrique de raison \(q=1-h\). On sait qu’une telle suite

• diverge si \(|q|>1\) ou \(q=-1\),
• est stationnaire si \(q=1\),
• converge vers \(0\) si \(|q|<1\).
• converge de façon monotone vers \(0\) si \(0<q<1\).

Voyons graphiquement ce que cela donne avec différentes valeurs de \(h>0\) :

• si \(h=4\) alors \(t_n=4n\) et \(u_{n}=\left(-4\right)^{n}\) tandis que \(y(t_{n})=e^{-4n}\),
• si \(h=2\) alors \(t_n=2n\) et \(u_{n}=\left(-1\right)^{n}\) tandis que \(y(t_{n})=e^{-2n}\),
• si \(h=1\) alors \(t_n=n\) et \(u_{n}=0\) tandis que \(y(t_{n})=e^{-n}\),
• si \(h=\frac{1}{2}\) alors \(t_n=\frac{n}{2}\) et \(u_{n}=\left(\dfrac{1}{2}\right)^{n}\) tandis que \(y(t_{n})=e^{-n/2}\),
• si \(h=\frac{1}{4}\) alors \(t_n=\frac{n}{4}\) et \(u_{n}=\left(\dfrac{3}{4}\right)^{n}\) tandis que \(y(t_{n})=e^{-n/4}\).

Ci-dessous sont tracées sur l’intervalle \([0;10]\), les courbes représentatives de la solution exacte et de la solution calculée par la méthode d’Euler explicite. En faisant varier le pas \(h\) nous pouvons constater que si \(h>1\) l’erreur commise entre la solution exacte et la solution calculée est amplifiée d’un pas à l’autre.

Remarque : la première itérée a la même pente quel que soit le pas \(h\) (se rappeler la construction géométrique de la méthode d’Euler).

# SCHEMA
def EE(phi,tt,y0):
    h = tt[1]-tt[0]
    uu = np.zeros_like(tt)  
    uu[0] = y0
    for i in range(len(tt)-1):
        uu[i+1] = uu[i]+h*phi(tt[i],uu[i])
    return uu


# CALCUL DE LA SOLUTION SUR CHAQUE GRILLE
U = [ EE(phi,tt,y0) for tt in T ] 
     
# AFFICHAGE
plt.figure(1, figsize=(15, 10))
plt.axis([t0, tfinal, -1, 1])

plt.plot(T[0],yy,'-',label='$y(t)=e^{-t}$')
for k in range(5):
    plt.plot(T[k],U[k],'-o',label=f'h = {</span>H[k]<span class="sc">}')
plt.legend()
plt.grid();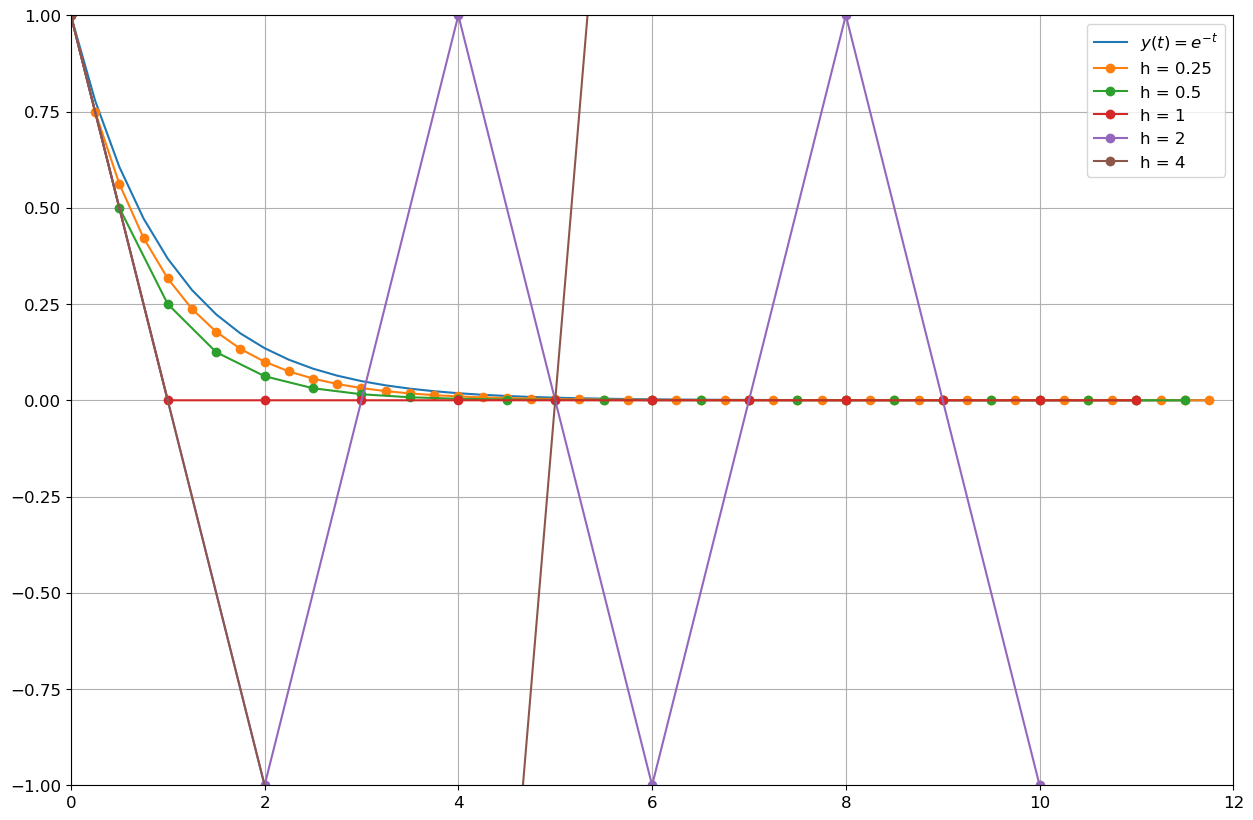

Solution approchée par la méthode d’Euler implicite

La méthode d’Euler implicite pour cette EDO s’écrit

\( u_{n+1}=\frac{1}{1+h}u_n. \)

En procédant par récurrence sur \(n\), on obtient

\( u_{n+1}=\frac{1}{(1+h)^{n+1}}. \)

De la formule \(u_{n+1}=(1+h)^{-(n+1)}\) on déduit que la solution numérique est stable et convergente pour tout \(h\). En effet, la méthode est inconditionnellement A-stable.

Remarque : la suite obtenue est une suite géométrique de raison \(q=\frac{1}{1+h}\in]0;1[\).

# SCHEMA
def EI(phi,tt,y0):
    h = tt[1]-tt[0]
    uu = np.zeros_like(tt)
    uu[0] = y0
    for i in range(len(tt)-1):
        uu[i+1] = fsolve(lambda x:-x+uu[i]+h*phi(tt[i+1],x),uu[i])[0]   
    return uu


# CALCUL DE LA SOLUTION SUR CHAQUE GRILLE
U = [ EI(phi,tt,y0) for tt in T ] 
     
# AFFICHAGE
plt.figure(1, figsize=(15, 10))
plt.axis([t0, tfinal, -1, 1])

plt.plot(T[0],yy,'-',label='$y(t)=e^{-t}$')
for k in range(5):
    plt.plot(T[k],U[k],'-o',label=f'h = {</span>H[k]<span class="sc">}')
plt.legend()
plt.grid();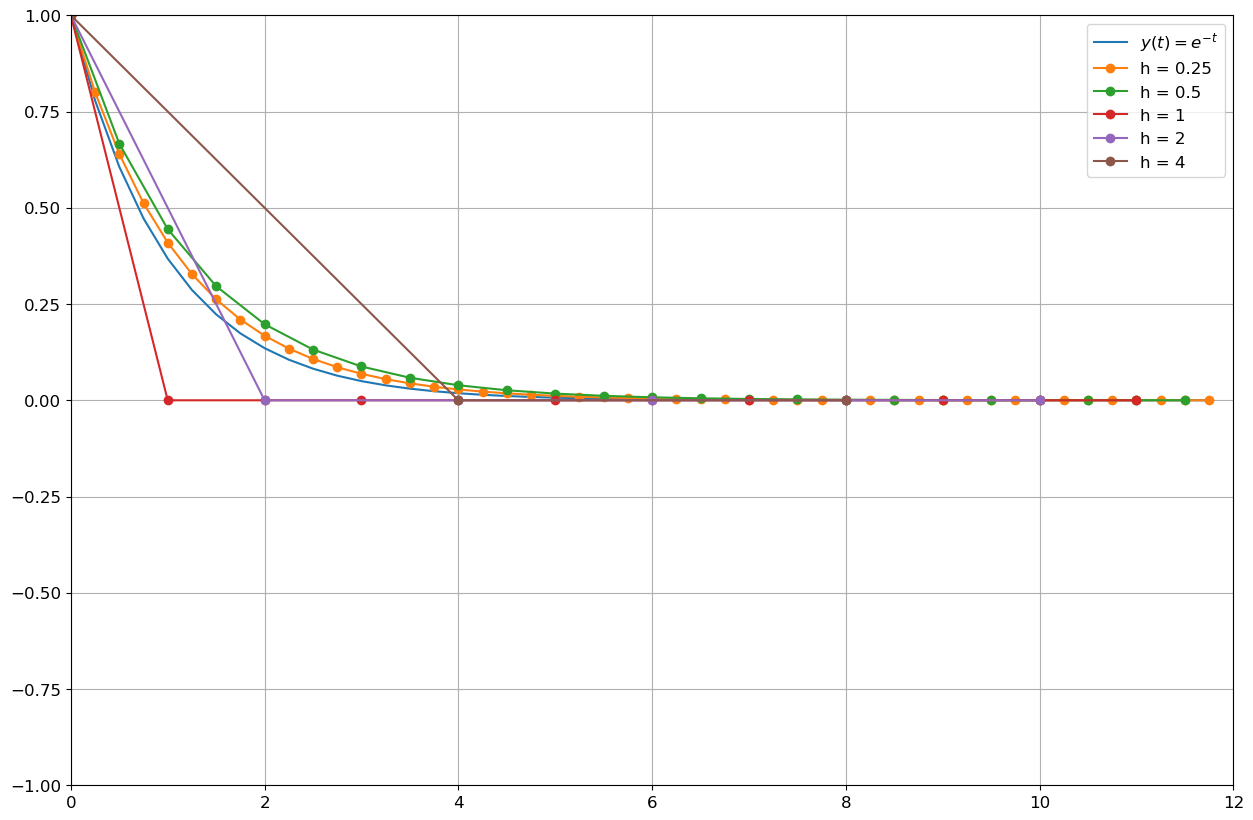

Solution approchée par la méthode d’Euler modifié

La méthode d’Euler modifié pour cette EDO s’écrit

\( u_{n+1}=(1-h+\frac{1}{2}h^2)u_n. \)

En procédant par récurrence sur \(n\), on obtient

\( u_{n+1}=(1-h+\frac{1}{2}h^2)^{n+1}. \)

La suite obtenue est une suite géométrique de raison \(q=1-h+\frac{1}{2}h^2\):

• si \(0<h<2\) alors la solution numérique est stable et convergente,
• si \(h=2\) alors la solution numérique est stationnaire \(u_n=u_0\) pour tout \(n\in\mathbb{N}^*\),
• si \(h>2\) alors la solution numérique diverge vers \(+\infty\).

En effet, la méthode est A-stable si et seulement si \(|1-h+\frac{1}{2}h^2| < 1\). De plus, comme \(1-h+\frac{1}{2}h^2>0\) pour tout \(h>0\), la suite est positive.

# SCHEMA
def EM(phi,tt,y0):
    h = tt[1]-tt[0]
    uu = np.zeros_like(tt)
    uu[0] = y0
    for i in range(len(tt)-1):
        utilde = uu[i]+h/2*phi(tt[i],uu[i])
        uu[i+1] = uu[i]+h*phi(tt[i]+h/2,utilde)
    return uu


# CALCUL DE LA SOLUTION SUR CHAQUE GRILLE
U = [ EM(phi,tt,y0) for tt in T ] 
     
# AFFICHAGE
plt.figure(1, figsize=(15, 10))
plt.axis([t0, tfinal, -1, 2])

plt.plot(T[0],yy,'-',label='$y(t)=e^{-t}$')
for k in range(5):
    plt.plot(T[k],U[k],'-o',label=f'h = {</span>H[k]<span class="sc">}')
plt.legend()
plt.grid();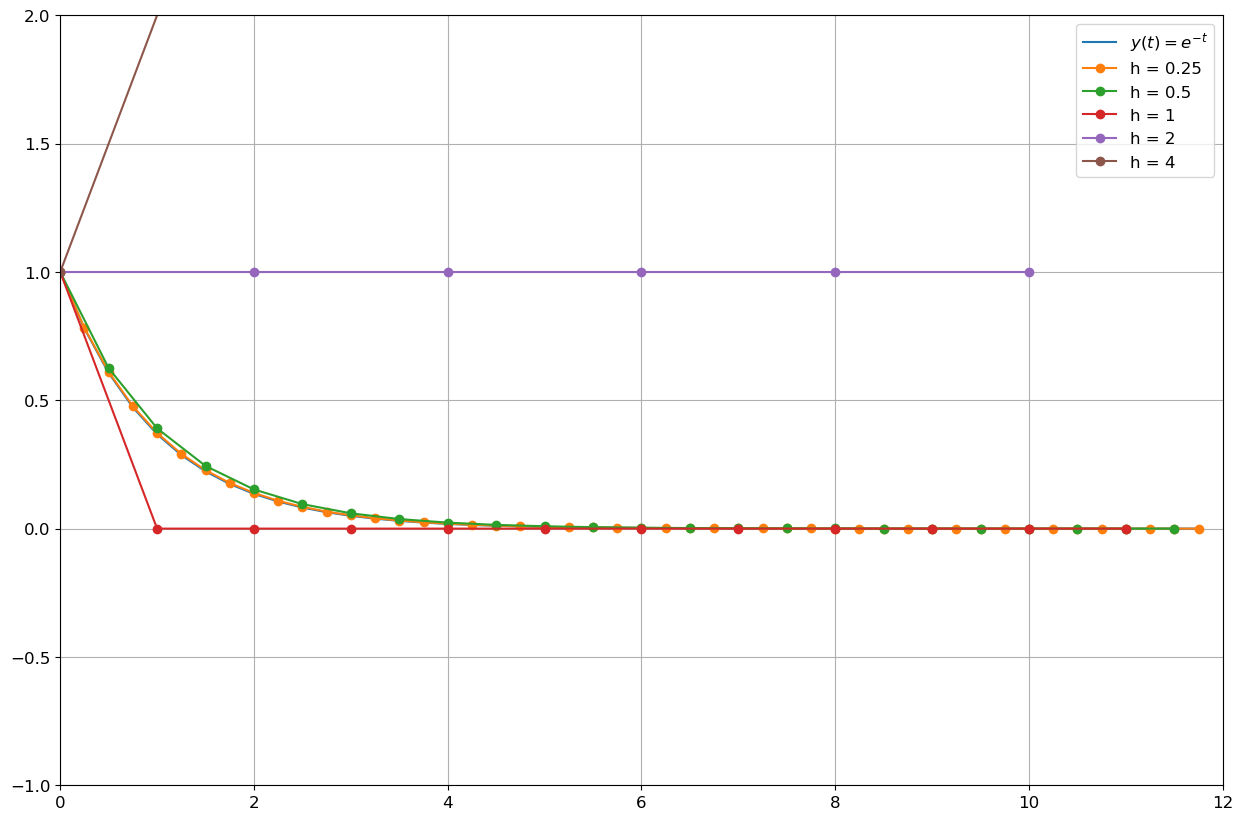

Solution approchée par la méthode de Crank-Nicolson

La méthode de Crank-Nicolson pour cette EDO s’écrit

\( u_{n+1}=\frac{2-h}{2+h}u_n. \)

En procédant par récurrence sur \(n\), on obtient

\( u_{n+1}=\left(\frac{2-h}{2+h}\right)^{n+1}. \)

La suite obtenue est une suite géométrique de raison \(q=\frac{2-h}{2+h}\in]-1;1[\). On déduit que la solution numérique est stable et convergente pour tout \(h\). En effet, la méthode est inconditionnellement A-stable.

De plus, la suite est positive ssi \(0<q<1\) donc ssi \(h<2\).

# SCHEMA
def CN(phi,tt,y0):
    h = tt[1]-tt[0]
    uu = np.zeros_like(tt)
    uu[0] = y0
    for i in range(len(tt)-1):
        uu[i+1] = fsolve(lambda x:-x+uu[i]+h/2*phi(tt[i],uu[i])+h/2*phi(tt[i+1],x),uu[i])[0]
    return uu   


# CALCUL DE LA SOLUTION SUR CHAQUE GRILLE
U = [ CN(phi,tt,y0) for tt in T ] 
     
# AFFICHAGE
plt.figure(1, figsize=(15, 10))
plt.axis([t0, tfinal, -1, 1])

plt.plot(T[0],yy,'-',label='$y(t)=e^{-t}$')
for k in range(5):
    plt.plot(T[k],U[k],'-o',label=f'h = {</span>H[k]<span class="sc">}')
plt.legend()
plt.grid();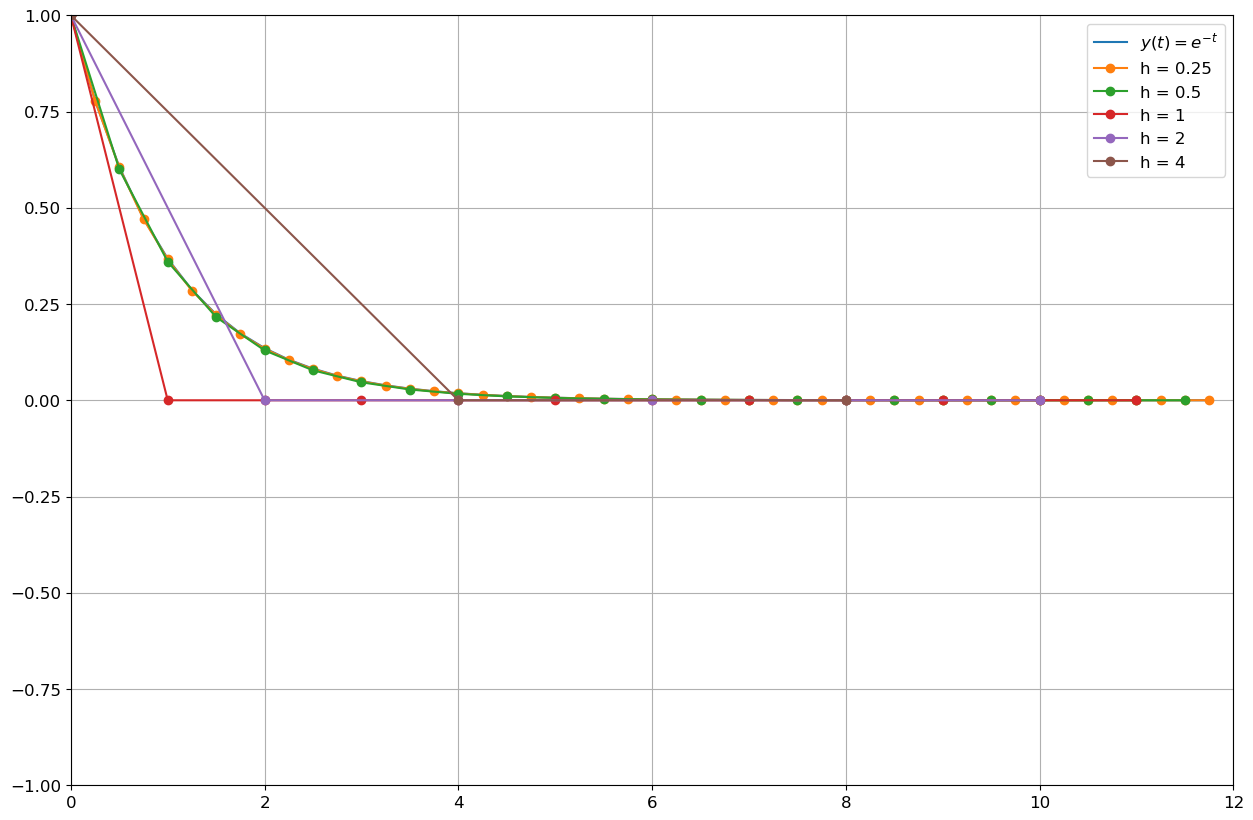

Solution approchée par la méthode de Heun

La méthode de Heun pour cette EDO s’écrit

\( u_{n+1}=(1-h+\frac{1}{2}h^2)u_n. \)

On retrouve le schéma d’Euler modifié.