🚢 Analyse statistique et visualisation : le jeu de données du Titanic

Auteur·rice

Gloria FACCANONI

Date de publication

6 décembre 2025

Nous allons effectuer une analyse exploratoire approfondie (EDA) de l’ensemble de données relatives au naufrage du Titanic. Notre objectif est d’étudier les données en détail et de voir comment même des observations simples peuvent révéler des informations précieuses.

Le naufrage du Titanic est l’un des plus célèbres de l’histoire. Le 15 avril 1912, lors de son voyage inaugural, le RMS Titanic, un paquebot transatlantique britannique, a sombré après être entré en collision avec un iceberg, tuant 1502 passagers et membres d’équipage sur 2224. (Selon Wikipedia il y avait 1316 passagers et 889 membres d’équipage, ce qui donne 2205 personnes) L’une des raisons pour lesquelles le naufrage a causé tant de morts est qu’il n’y avait pas assez de canots de sauvetage pour les passagers et l’équipage. On a toujours entendu dire que certains groupes de personnes étaient plus susceptibles de survivre que d’autres, comme les femmes, les enfants et les classes supérieures. Nous allons analyser les données pour vérifier ces affirmations.

Dans cet exemple, nous allons récupérer un jeu de données (liste de personnes, caractéristiques, survivants ou non…) et analyser quelles catégories de personnes ont survécu. Nous utiliserons les bibliothèques pandas, Matplotlib, Seaborn et Plotly pour explorer et visualiser ces données.

1 Importation des données

# Import data analysis libraries
# ==============================
import numpy as np
import pandas as pd 
pd.set_option("display.max_columns", None)


# Import visualization libraries and set favourite style
# ======================================================
import matplotlib.pyplot as plt
plt.rcParams['font.size'] = 12
plt.rcParams['figure.figsize'] = (10, 6) # set default size of plots
# plt.style.use('ggplot') # set ggplot style

import seaborn as sns
sns.set_theme(style = "ticks", # "ticks", "whitegrid", "darkgrid", "white", "dark"
              palette = "pastel", # None, Set2, husl, deep, muted, bright, pastel, dark, colorblind
              rc = {"axes.spines.right": False, "axes.spines.top": False})


import plotly.express as px
from plotly.subplots import make_subplots

# Import Notebook display library
# ==============================
from IPython.display import display, Markdown


# Pour la génération automatique de graphiques interactifs dans le polycopié
# ==============================
# import plotly.io as pio
# import os
# if os.getenv("QUARTO_OUTPUT_FORMAT") is not None:
#     # Export Quarto HTML
#     pio.renderers.default = "iframe_connected"
# else:
#     # Notebook interactif
#     pio.renderers.default = "notebook_connected"

L’une des forces de pandas est l’importation et l’exportation des données. Ce package possède un ensemble de fonctions très large pour charger des données en mémoire et les exporter dans divers formats.

Pandas dédie un sous-répertoire entier du package à l’importation et à l’exportation vers des formats de données exploitables avec d’autres outils. On peut citer les formats csv, txt, Excel®, SAS®, SQL, HDF5 entre autres. Suivant le format, les outils seront différents, mais les principes restent les mêmes. Ainsi, nous allons considérer uniquement le format csv.

Un fichier CSV (.csv) est un fichier de données tabulaires. Le sigle CSV signifie Comma Separated Values qui se traduit par « valeurs séparées par des virgules ». L’avantage de ce type de fichier est qu’il s’agit d’un fichier texte qui ne conserve que les données du tableau (pas de mise en page) et peut être lu par n’importe quel tableur. Les données d’une même ligne sont souvent séparées par des points-virgules ou des virgules.

Pour importer les données stockées dans un fichier csv dont les éléments sont séparés par des virgules, on utilisera :

df = pd.read_csv('nom_du_fichier.csv', sep=',')

Dans l’exemple suivant nous allons importer et afficher un fichier csv contenant des données sur le Titanic.

df = pd.read_csv('titanic.csv')

2 Étude globale de l’ensemble de données

Dans cette partie nous allons utiliser les méthodes suivantes :

.shape
.info()
.head() .tail()
.columns
.isnull() .dropna() .fillna()
.unique() .nunique() .value_counts()
.describe() .min(), .max(), .mean(), .median(), .std()

La première étape de tout projet d’analyse de données consiste à examiner les données. Nous devons voir combien d’observations (lignes) et combien d’entités (colonnes) sont contenues, ce que signifient ces colonnes, et ainsi de suite. Cela nous aidera à nous familiariser avec l’ensemble de données, et pourrait même nous aider à évaluer quelles informations sont importantes et lesquelles ne le sont pas.

df.shape # tailles du dataset : 1309 lignes et 7 colonnes
# df.columns

(1309, 7)

Un moyen rapide de vérifier le contenu consiste à appeler les 5 premières lignes à l’aide de la méthode .head() sans spécifier l’argument entre parenthèses. Si nous voulons vérifier les 20 premières lignes, nous mettons 20 comme argument.

# df
df.head(20)
# df.tail(10)

	classe	survivant	nom	sexe	age	prix	port_depart
0	1	1	Allen, Miss. Elisabeth Walton	F	29.0000	211.3375	S
1	1	1	Allison, Master. Hudson Trevor	H	0.9167	151.5500	S
2	1	0	Allison, Miss. Helen Loraine	F	2.0000	151.5500	S
3	1	0	Allison, Mr. Hudson Joshua Creighton	H	30.0000	151.5500	S
4	1	0	Allison, Mrs. Hudson J C (Bessie Waldo Daniels)	F	25.0000	151.5500	S
5	1	1	Anderson, Mr. Harry	H	48.0000	26.5500	S
6	1	1	Andrews, Miss. Kornelia Theodosia	F	63.0000	77.9583	S
7	1	0	Andrews, Mr. Thomas Jr	H	39.0000	0.0000	S
8	1	1	Appleton, Mrs. Edward Dale (Charlotte Lamson)	F	53.0000	51.4792	S
9	1	0	Artagaveytia, Mr. Ramon	H	71.0000	49.5042	C
10	1	0	Astor, Col. John Jacob	H	47.0000	227.5250	C
11	1	1	Astor, Mrs. John Jacob (Madeleine Talmadge Force)	F	18.0000	227.5250	C
12	1	1	Aubart, Mme. Leontine Pauline	F	24.0000	69.3000	C
13	1	1	Barber, Miss. Ellen "Nellie"	F	26.0000	78.8500	S
14	1	1	Barkworth, Mr. Algernon Henry Wilson	H	80.0000	30.0000	S
15	1	0	Baumann, Mr. John D	H	NaN	25.9250	S
16	1	0	Baxter, Mr. Quigg Edmond	H	24.0000	247.5208	C
17	1	1	Baxter, Mrs. James (Helene DeLaudeniere Chaput)	F	50.0000	247.5208	C
18	1	1	Bazzani, Miss. Albina	F	32.0000	76.2917	C
19	1	0	Beattie, Mr. Thomson	H	36.0000	75.2417	C

On compte 7 caractéristiques (colonnes) décrivant chaque personne à bord du Titanic. Notre caractéristique cible (également appelée variable dépendante) est la colonne survivant, qui vaut 1 si la personne a survécu et 0 sinon. Dans ce cas, il est facile de déduire que cette colonne ne contient que des valeurs numériques 0 et 1. Cependant, pour d’autres caractéristiques (ou variables indépendantes), il peut ne pas être possible de déduire au premier coup d’œil le type de données contenues.

Afin de générer rapidement un tableau des types de données contenus dans chaque colonne, nous utilisons la méthode .info().

# Info about data frame dimensions, column types, and file size

df.info()

<class 'pandas.core.frame.DataFrame'>
RangeIndex: 1309 entries, 0 to 1308
Data columns (total 7 columns):
 #   Column       Non-Null Count  Dtype  
---  ------       --------------  -----  
 0   classe       1309 non-null   int64  
 1   survivant    1309 non-null   int64  
 2   nom          1309 non-null   object 
 3   sexe         1309 non-null   object 
 4   age          1046 non-null   float64
 5   prix         1308 non-null   float64
 6   port_depart  1307 non-null   object 
dtypes: float64(2), int64(2), object(3)
memory usage: 71.7+ KB

2.1 Données manquantes ?

Combien de valeurs manquantes dans chaque colonne ?

df.isnull().sum().sort_values(ascending=False).to_frame('Données manquantes')

	Données manquantes
age	263
port_depart	2
prix	1
classe	0
survivant	0
nom	0
sexe	0

Il est utile d’utiliser la méthode .isnull() combinée avec .sum() ou .mean() pour connaître l’ampleur des valeurs manquantes dans un jeu de données.

(df.isnull().mean().sort_values(ascending = False) * 100).round(2).sort_values(ascending=False).to_frame('% données manquantes')

	% données manquantes
age	20.09
port_depart	0.15
prix	0.08
classe	0.00
survivant	0.00
nom	0.00
sexe	0.00

Nous pouvons voir que la colonne port_depart contient 2 valeurs manquantes (indiquées par NaN). Qui sont les passagers pour lesquels on n’a pas ces informations ?

# mask = df['age'].isnull()
# df.loc[mask] # il y a 263 valeurs manquantes pour l'age, car 1309-1046=263

mask = df['port_depart'].isnull()
df.loc[mask]

	classe	survivant	nom	sexe	age	prix	port_depart
168	1	1	Icard, Miss. Amelie	F	38.0	80.0	NaN
284	1	1	Stone, Mrs. George Nelson (Martha Evelyn)	F	62.0	80.0	NaN

De même, nous pouvons voir que dans la colonne age il manque 263 données (nous n’allons pas les afficher). Peut-être que ces données n’ont pas été collectées ou ont été perdues. Que faire ? Nous pourrions soit supprimer ces lignes, soit remplacer les valeurs manquantes par la moyenne de l’âge des passagers par exemple. Les choix relatifs au traitement des valeurs manquantes ne sont pas des choix méthodologiques neutres. Pandas donne les outils techniques pour faire ceci mais la question de la légitimité de ces choix et de leur pertinence est propre à chaque jeu de données.

Pour le moment nous n’allons pas modifier les données.

# Option 1 : éliminer les lignes avec des valeurs manquantes
# df = df.dropna(axis=0)
# df.shape  # (1046, 7)

# Option 2 : remplacer par la moyenne (Attention : on modifie la réalité)
# df.fillna(df['age'].mean(), inplace=True)

2.2 Bilan sur l’ensemble de données

Conclusion : nous savons maintenant que ce jeu de données comporte 1309 lignes et 7 colonnes. 4 colonnes sont de type numérique (flottants et entiers), 3 colonnes sont non numériques :

classe : valeurs possibles 1, 2 ou 3
survivant : 0 (décédé), 1 (a survécu)
nom : nom, prénom et titre
sexe : H (homme), F (femme)
age : en années
prix : prix du ticket
port_depart : trois ports d’embarquement, C = Cherbourg (France), S = Southampton (Angleterre), Q = Queenstown (Irlande)

2.3 Statistiques descriptives

Pour les colonnes numériques telles que age, prix, etc., nous aimerions connaître leurs valeurs moyennes, maximales et minimales pour voir si les données sont raisonnablement distribuées ou s’il y a des anomalies. Pour afficher un tableau de statistiques pour chaque colonne numérique, nous utilisons la méthode .describe().

# df.describe(include='all')
display(df.describe().T)
display(df.describe(include='object').T)
# df.describe(include="all")

	count	mean	std	min	25%	50%	75%	max
classe	1309.0	2.294882	0.837836	1.0000	2.0000	3.0000	3.000	3.0000
survivant	1309.0	0.381971	0.486055	0.0000	0.0000	0.0000	1.000	1.0000
age	1046.0	29.881135	14.413500	0.1667	21.0000	28.0000	39.000	80.0000
prix	1308.0	33.295479	51.758668	0.0000	7.8958	14.4542	31.275	512.3292

	count	unique	top	freq
nom	1309	1307	Connolly, Miss. Kate	2
sexe	1309	2	H	843
port_depart	1307	3	S	914

On note que la colonne prix a une valeur minimale de 0, ce qui semble étrange. Cela pourrait signifier que certaines personnes ont voyagé gratuitement.

3 Analyse univariée (chaque colonne individuellement)

Commençons par l’analyse univariée, qui consiste à explorer une seule variable à la fois. Cela nous aide à comprendre la distribution, les tendances et les caractéristiques sous-jacentes de cette variable. En traçant et en analysant les courbes d’une caractéristique, nous pouvons obtenir des informations précieuses sur les données avant de passer à des relations plus complexes.

Dans cette partie nous allons utiliser les méthodes suivantes :

.drop() .replace()
.value_counts()
.agg()
.cut() .map()
.plot(kind='bar') .plot(kind='hist')
sns.countplot() sns.catplot() sns.histplot()
px.histogram() px.pie()

Tout d’abord nous allons examiner la colonne nom pour retrouver des informations intéressantes sur les passagers (en vérifiant les informations indiquées sur le site https://titanicfacts.net/titanic-passengers/). Ensuite, nous analyserons les autres colonnes une par une. Nous nous intéresserons particulièrement aux colonnes classe, sexe, survivant, age et verrons ensuite comment ces caractéristiques influencent les chances de survie des passagers.

3.1 Colonne `nom`

3.1.1 Plus jeune et plus vieux passagers

Une autre valeur qui attire l’attention est l’âge minimum, soit 0,1667 ans, avec un éventuel bébé de 9 semaines à bord. De plus amples informations sur https://titanicfacts.net/titanic-passengers/ indiquent qu’il s’agit de Elizabeth Gladys “Milvina” Dean, une fille âgée de 2 mois et 13 jours au moment du naufrage (qui est décédée en 2009 à l’âge de 97 ans). Vérifions si cette information est correcte :

# mask_idx = df['age'].idxmin()  # index de la personne la plus jeune
# df.iloc[mask_idx]

mask = df['age'] == df['age'].min()
df.loc[mask]

	classe	survivant	nom	sexe	age	prix	port_depart
763	3	1	Dean, Miss. Elizabeth Gladys "Millvina"	F	0.1667	20.575	S

Et le plus jeune passager garçon ? Toujours selon le site précédent, il s’agit de Master Gilbert Sigvard Emanuel Danbom, âgé de 4 mois et 29 jours, qui n’a malheureusement pas survécu. Vérifions si cette information est correcte :

# Filtrer les individus dont sex == "H"
filtered_df = df.loc[df['sexe'] == "H"]
# Trouver l'âge minimum dans cette sous-table
min_age = filtered_df['age'].min()
# Sélectionner les lignes correspondant à cet âge minimum
youngest = filtered_df.loc[filtered_df['age'] == min_age]
# Afficher les résultats
youngest

	classe	survivant	nom	sexe	age	prix	port_depart
747	3	0	Danbom, Master. Gilbert Sigvard Emanuel	H	0.3333	14.4	S

Et le passager le plus âgé ?

df.loc[df['age']==df['age'].max()]

	classe	survivant	nom	sexe	age	prix	port_depart
14	1	1	Barkworth, Mr. Algernon Henry Wilson	H	80.0	30.0	S

Selon le site précédent, il s’agit de Mr Johan Svensson, âgé de 74 ans et 10 mois, qui n’a pas survécu. Cependant, notre jeu de données ne contient pas cette information :

df[df['nom'].str.contains('Svensson', case=False, na=False)]

	classe	survivant	nom	sexe	age	prix	port_depart
979	3	0	Lundahl, Mr. Johan Svensson	H	51.0	7.0542	S
1235	3	0	Svensson, Mr. Johan	H	74.0	7.7750	S
1236	3	1	Svensson, Mr. Johan Cervin	H	14.0	9.2250	S
1237	3	0	Svensson, Mr. Olof	H	24.0	7.7958	S

Et la femme la plus âgée ?

# Filtrer les individus dont sex == "F"
filtered_df = df.loc[df['sexe'] == "F"]
# Trouver l'âge maximum dans cette sous-table
max_age = filtered_df['age'].max()
# Sélectionner les lignes correspondant à cet âge maximum
oldest = filtered_df.loc[filtered_df['age'] == max_age]
# Afficher les résultats
oldest

	classe	survivant	nom	sexe	age	prix	port_depart
61	1	1	Cavendish, Mrs. Tyrell William (Julia Florence...	F	76.0	78.85	S

Selon le site il s’agit de Mrs Mary Eliza Compton, âgée de 64 ans et 8 mois, qui a survécu. À nouveau, notre jeu de données ne contient pas cette information :

df[df['nom'].str.contains('Compton', case=False, na=False)]

	classe	survivant	nom	sexe	age	prix	port_depart
76	1	1	Compton, Miss. Sara Rebecca	F	39.0	83.1583	C
77	1	0	Compton, Mr. Alexander Taylor Jr	H	37.0	83.1583	C
78	1	1	Compton, Mrs. Alexander Taylor (Mary Eliza Ing...	F	64.0	83.1583	C

3.1.2 Plus jeune et plus vieux passagers à avoir survécu

# parmi les survivants, qui est le plus jeune et qui est le plus âgé ? 
survivants = df[df['survivant'] == 1]
# plus jeune
min_age_survivant = survivants['age'].min()
plus_jeune_survivant = survivants[survivants['age'] == min_age_survivant]
display(Markdown("**Plus jeune survivant :**"))
display(plus_jeune_survivant)
# plus âgé
max_age_survivant = survivants['age'].max()
plus_vieux_survivant = survivants[survivants['age'] == max_age_survivant]
display(Markdown("**Plus vieux survivant :**"))
display(plus_vieux_survivant)

Plus jeune survivant :

	classe	survivant	nom	sexe	age	prix	port_depart
763	3	1	Dean, Miss. Elizabeth Gladys "Millvina"	F	0.1667	20.575	S

Plus vieux survivant :

	classe	survivant	nom	sexe	age	prix	port_depart
14	1	1	Barkworth, Mr. Algernon Henry Wilson	H	80.0	30.0	S

3.1.3 Plus jeune et plus vieux passagers à être décédé

# parmi les decede, qui est le plus jeune et qui est le plus âgé ? 
decede = df[df['survivant'] == 0]
# plus jeune
min_age_decede = decede['age'].min()
plus_jeune_decede = decede[decede['age'] == min_age_decede]
display(Markdown("**Plus jeune décédé :**"))
display(plus_jeune_decede)
# plus âgé
max_age_decede = decede['age'].max()
plus_vieux_decede = decede[decede['age'] == max_age_decede]
display(Markdown("**Plus vieux décédé :**"))
display(plus_vieux_decede)

Plus jeune décédé :

	classe	survivant	nom	sexe	age	prix	port_depart
747	3	0	Danbom, Master. Gilbert Sigvard Emanuel	H	0.3333	14.4	S

Plus vieux décédé :

	classe	survivant	nom	sexe	age	prix	port_depart
1235	3	0	Svensson, Mr. Johan	H	74.0	7.775	S

3.1.4 Le capitaine du Titanic ?

Si on cherche dans notre jeu de données le titre capitaine, on trouve le passager suivant :

df[df['nom'].str.contains('Capt', case=False, na=False)]

	classe	survivant	nom	sexe	age	prix	port_depart
81	1	0	Crosby, Capt. Edward Gifford	H	70.0	71.0	S

Ce n’est pas le capitaine du Titanic qui était Edward John Smith (1850-1912) mais il n’apparaît pas dans notre jeu de données.

df[df['nom'].str.contains('Smith', case=True, na=False)]

	classe	survivant	nom	sexe	age	prix	port_depart
267	1	0	Smith, Mr. James Clinch	H	56.0	30.6958	C
268	1	0	Smith, Mr. Lucien Philip	H	24.0	60.0000	S
269	1	0	Smith, Mr. Richard William	H	NaN	26.0000	S
270	1	1	Smith, Mrs. Lucien Philip (Mary Eloise Hughes)	F	18.0	60.0000	S
564	2	1	Smith, Miss. Marion Elsie	F	40.0	13.0000	S
1215	3	0	Smith, Mr. Thomas	H	NaN	7.7500	Q

3.1.5 Curiosités

Sur Wikipedia, à la page https://fr.m.wikipedia.org/wiki/Violet_Constance_Jessop il est indiqué que Violet Constance Jessop (2 octobre 1887 - 5 mai 1971), une hôtesse et infirmière britannique de la White Star Line, a survécu aux trois naufrages des navires de la classe Olympic. En effet, elle sert comme hôtesse à bord de l’Olympic quand il heurte le croiseur HMS Hawke le 20 septembre 1911. Elle se trouve également à bord du Titanic lorsqu’il fait naufrage le 15 avril 1912, et sert en tant qu’infirmière volontaire à bord du Britannic lorsqu’il fait naufrage en mer Égée le 21 novembre 1916.

Vérifions si elle apparaît dans notre jeu de données :

df[df['nom'].str.contains('Violet', case=False, na=False)]

	classe	survivant	nom	sexe	age	prix	port_depart
501	2	1	Mellinger, Miss. Madeleine Violet	F	13.0	19.5	S

La seule Violet dans notre jeu de données est une passagère de 13 ans, qui a embarqué à Southampton en 2ème classe. Elle a survécu au naufrage du Titanic mais n’est probablement pas la même personne que Violet Jessop.

Et Molly (Margaret Tobin) Brown (1867-1932) ? Elle est connue pour être l’une des rescapées du naufrage du Titanic. Sauvée à bord du canot n° 6, dans lequel elle déplore le comportement du quartier-maître Robert Hichens, elle participe ensuite à la création du Comité des Survivants. Un siècle après le naufrage, Margaret Brown est presque exclusivement surnommée l’« Insubmersible Molly Brown », bien qu’elle n’ait jamais été appelée ainsi de son vivant. Il s’agit d’une invention du cinéma hollywoodien, qui s’empare de son histoire pour en faire un mythe, parfois très éloigné de la vérité, notamment dans la comédie musicale La Reine du Colorado (1964) et le drame Titanic (1997).

df[df['nom'].str.contains('Tobin', case=False, na=False)]

	classe	survivant	nom	sexe	age	prix	port_depart
41	1	1	Brown, Mrs. James Joseph (Margaret Tobin)	F	44.0	27.7208	C
1249	3	0	Tobin, Mr. Roger	H	NaN	7.7500	Q

3.1.6 Doublons ?

df['nom'].nunique(), df['nom'].count()  # 1307 noms différents pour 1309 passagers

(1307, 1309)

On constate que la colonne nom contient 1307 valeurs uniques pour 1309 lignes, ce qui indique la présence de doublons. Affichons les lignes concernées pour examiner ces cas particuliers :

# keep=False signifie que chaque valeur de la colonne qui apparaît plus d'une fois sera marquée comme True
# Les valeurs uniques (apparaissant une seule fois) seront marquées comme False
mask = df['nom'].duplicated(keep=False)
df[mask]

	classe	survivant	nom	sexe	age	prix	port_depart
725	3	1	Connolly, Miss. Kate	F	22.0	7.7500	Q
726	3	0	Connolly, Miss. Kate	F	30.0	7.6292	Q
924	3	0	Kelly, Mr. James	H	34.5	7.8292	Q
925	3	0	Kelly, Mr. James	H	44.0	8.0500	S

3.1.7 Suppression de la colonne `nom`

Dans notre jeu de données, la colonne nom ne semble plus être pertinente pour l’analys qui va suivre. Nous pouvons la supprimer en utilisant la méthode .drop(). En effet, certaines colonnes peuvent être négligées si elles ne sont pas pertinentes pour l’analyse et inutile de les garder dans le DataFrame.

# errors="ignore" pour éviter une erreur si la colonne n'existe pas
df.drop('nom', axis='columns', inplace=True, errors="ignore")

3.2 Préambule: valeurs uniques dans chaque colonne

Pour chaque colonne, nous voulons connaître combien de valeurs différentes elle contient, lesquelles sont ces valeurs et combien de fois chacune apparaît.

Pour le nombre de valeurs différentes par colonne, nous avons :

df.nunique()

classe           3
survivant        2
sexe             2
age             98
prix           281
port_depart      3
dtype: int64

On note que la colonne classe ne contient que 3 valeurs différentes, la colonne survivant ne contient que 2 valeurs différentes, la colonne sexe ne contient que 2 valeurs différentes, la colonne port_depart ne contient que 3 valeurs différentes. Pour ces colonnes ayant moins de 5 valeurs différentes, nous pouvons lister quelles sont ces valeurs différentes en utilisant la méthode .unique() :

filtre = [df[col].nunique() < 5 for col in df.columns]

for col in df[df.columns[filtre]]:
    print(col, df[col].unique())

classe [1 2 3]
survivant [1 0]
sexe ['F' 'H']
port_depart ['S' 'C' nan 'Q']

Pour une colonne donnée, nous pouvons lister non seulement les valeurs différentes en utilisant la méthode .unique(), mais aussi compter le nombre d’occurrences de chaque valeurs différentes en utilisant la méthode .value_counts().

Pour analyser plus en profondeur une colonne catégorielle, il est utile d’afficher à la fois : - Le nombre absolu d’occurrences de chaque catégorie - Le pourcentage que représente chaque catégorie par rapport au total - Le traitement des valeurs manquantes (si présentes)

Comme ces informations sont intéressantes à afficher pour toute colonne catégorielle ou numérique discrète, nous allons créer une fonction réutilisable nommée afficher_compte_et_pourcentage() qui : 1. Calcule le nombre d’occurrences de chaque valeur unique 2. Calcule le pourcentage correspondant 3. Gère l’affichage des valeurs manquantes de manière explicite 4. Retourne un DataFrame synthétique facile à lire

Cette fonction sera ensuite appelée pour différentes colonnes en changeant simplement le nom de la colonne passée en paramètre.

def afficher_compte_et_pourcentage(df, colonne):
    compte = df[colonne].value_counts(dropna=False)
    pourcentage = df[colonne].value_counts(normalize=True, dropna=False) * 100
    resultat = pd.DataFrame({'Nb occurrences': compte, 'Pourcentage (%)': round(pourcentage, 2)})
    # Remplacer 'nan' dans l'index par 'Valeur manquante'
    resultat.index = resultat.index.map(lambda x: 'Valeur manquante' if pd.isna(x) else str(x))
    return resultat

3.3 Colonne `classe`

Combien de passagers étaient dans chaque classe ?

Dans la colonne classe seulement trois catégories sont possibles : 1, 2 ou 3. La méthode .value_counts() permet de compter le nombre d’occurrences pour chaque catégorie unique dans une colonne.

# Résumé statistique de la colonne 'classe'
# ================================================================

colonne = df['classe']

display(Markdown("**Résumé statistique de la colonne 'classe'**"))
display(colonne.describe().to_frame())

display(Markdown("**Nombre de valeurs uniques**"))
display(colonne.nunique())

display(Markdown("**Valeurs uniques**"))
display(colonne.unique())

display(Markdown("**Combien d'occurrences de chaque valeur unique**"))
display(colonne.value_counts().to_frame('Occurrences'))

display(Markdown("**Proportions des valeurs uniques**"))
display(colonne.value_counts(normalize=True).to_frame('Proportions'))  # proportions

Résumé statistique de la colonne ‘classe’

	classe
count	1309.000000
mean	2.294882
std	0.837836
min	1.000000
25%	2.000000
50%	3.000000
75%	3.000000
max	3.000000

Nombre de valeurs uniques

Valeurs uniques

array([1, 2, 3])

Combien d’occurrences de chaque valeur unique

	Occurrences
classe
3	709
1	323
2	277

Proportions des valeurs uniques

	Proportions
classe
3	0.541635
1	0.246753
2	0.211612

Selon le site Titanic Facts il est indiqué qu’il y avait 2222 personnes à bord du Titanic (passagers et équipage) dont 1327 de passagers effectivement à bord et répartis comme suit : 324 en première classe, 284 en deuxième classe et 709 en troisième classe. Il y avait 49% de places passagers inutilisées. Nos données semblent cohérentes avec ces informations.

afficher_compte_et_pourcentage(df, 'classe')

	Nb occurrences	Pourcentage (%)
classe
3	709	54.16
1	323	24.68
2	277	21.16

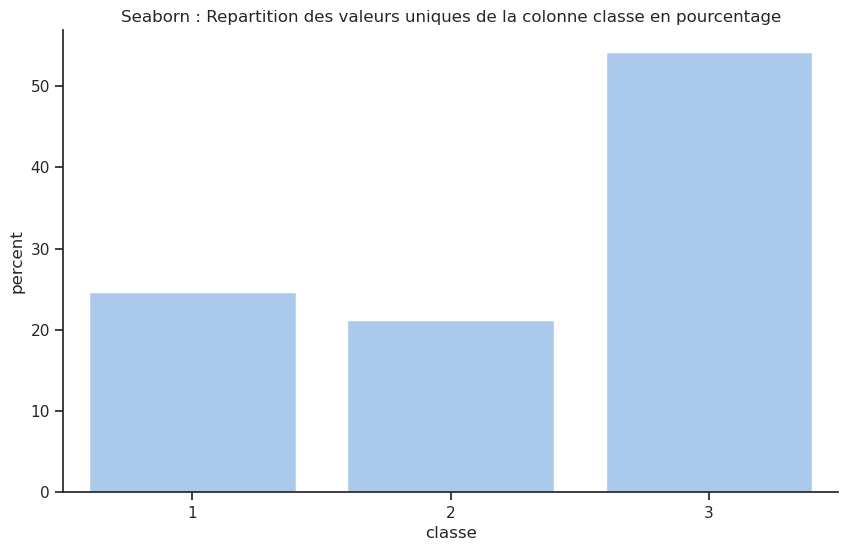
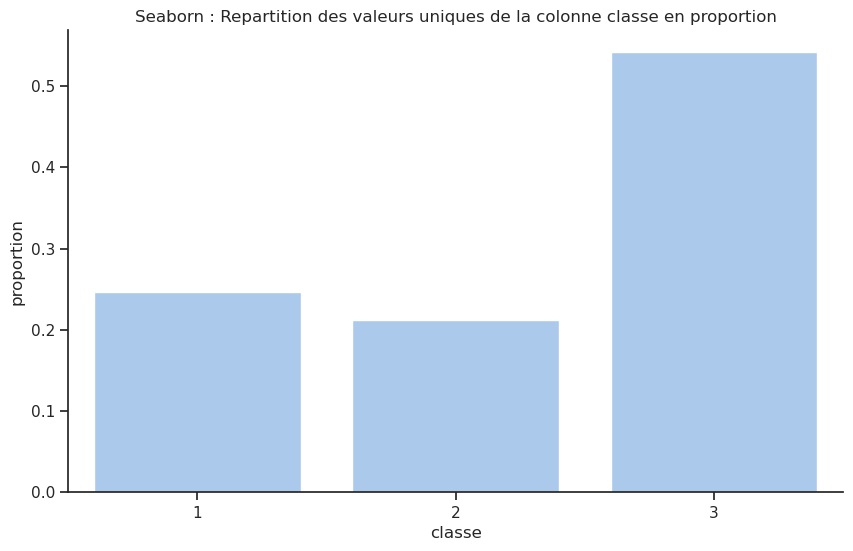
Ce tableau montre que la majorité des passagers (plus précisément 54 %) étaient de 3e classe. Fait intéressant, il y avait plus de passagers en première classe (323 passagers) qu’en seconde classe (277 passagers), même si la différence n’est pas très grande.

Pour avoir une idée visuelle du nombre de passagers par classe, on peut afficher ces informations

soit avec la fonction .plot() de pandas en spécifiant le type de graphique bar ou pie,
soit avec la fonction countplot() de Seaborn
soit avec les fonctions histogram() ou pie() de Plotly.

# Combien de fois chaque valeur unique apparaît dans la colonne ?
# ==================================================================

colonne = 'classe'

# Avec Pandas
# ------------------------------

# Avec la méthode value_counts() de la série, on peut obtenir le compte de chaque valeur unique dans la colonne.
df[colonne].value_counts().sort_index().plot(kind='bar');  # histogramme
plt.title(f'Pandas : Histogramme de la colonne {colonne}')
plt.show()


# Avec seaborn
# ------------------------------
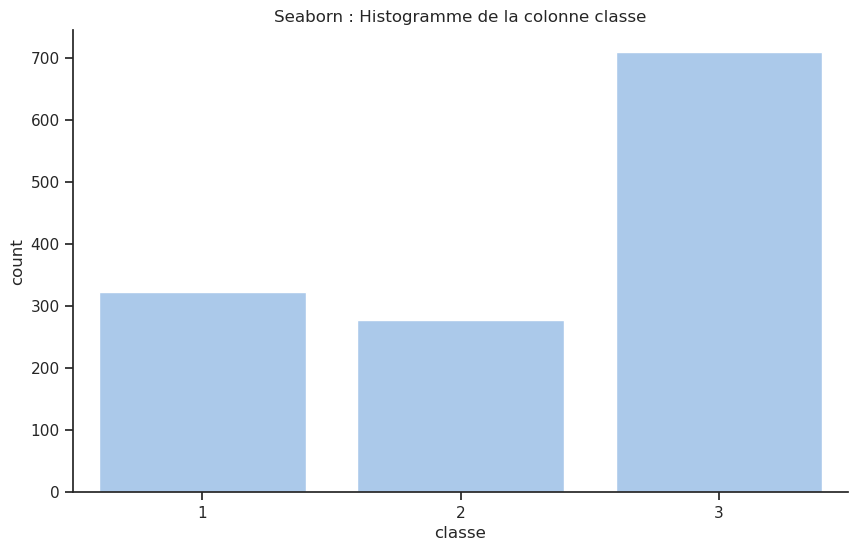
ax = sns.countplot(data=df, x=colonne); # histogramme
plt.title(f'Seaborn : Histogramme de la colonne {colonne}')
plt.show()
# Ajouter les annotations directement sur les barres
# for p in ax.patches:  # Les rectangles/barres sont dans ax.patches
#     ax.annotate(f'{int(p.get_height())}',  # Le texte est la hauteur de la barre
#                 (p.get_x() + p.get_width() / 2., p.get_height()),  # Position : centre de la barre
#                 ha='center', va='bottom', fontsize=10, color='black')  # Alignement et style


# Avec plotly.express
# ------------------------------
px.histogram(df, x=colonne, text_auto=True, title=f'Plotly : Histogramme de la colonne {colonne}').update_layout(bargap=0.2).show()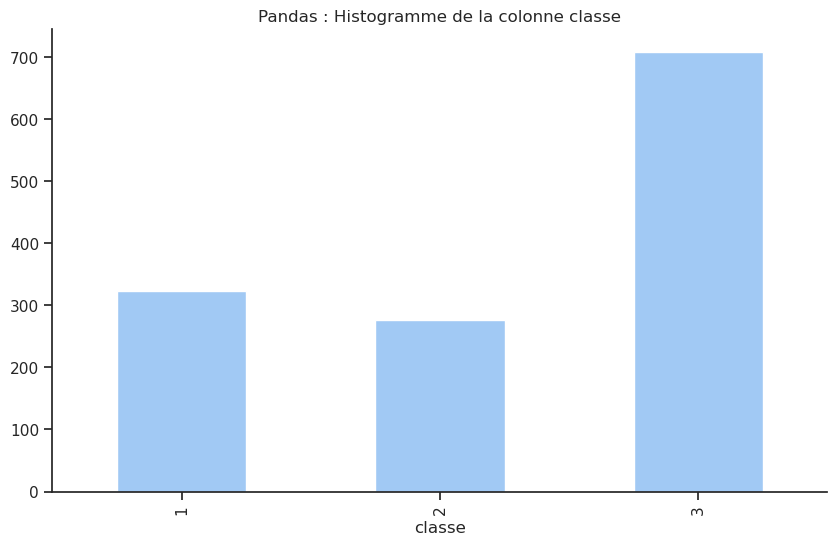

Unable to display output for mime type(s): application/vnd.plotly.v1+json

Et en pourcentage ?

# Repartition des valeurs uniques en pourcentage
# ==================================================================

colonne = 'classe'

# Avec Pandas et dans un camembert
# ------------------------------
df[colonne].value_counts().plot(kind='pie', 
                                 autopct='%1.2f%%',
                                 #explode=[0.1]*len(df[colonne].unique())
                                 )
plt.title(f'Pandas : Repartition des valeurs uniques de la colonne {colonne} en pourcentage')
plt.show();


# Avec seaborn
# ------------------------------
ax = sns.countplot(data=df, x=colonne, stat='percent'); # histogramme en pourcentage
plt.title(f'Seaborn : Repartition des valeurs uniques de la colonne {colonne} en pourcentage')
plt.show()
ax = sns.countplot(data=df, x=colonne, stat='proportion'); # histogramme en ptorportion
plt.title(f'Seaborn : Repartition des valeurs uniques de la colonne {colonne} en proportion')
plt.show()
# Note: Seaborn n'a pas de fonction native pour les diagrammes circulaires (pie charts)
# Il est recommandé d'utiliser matplotlib ou plotly pour ce type de visualisation


# Avec plotly.express
# ------------------------------
px.histogram(df, x='classe', histnorm='percent',title=f'Plotly : Repartition des valeurs uniques de la colonne {colonne} en pourcentage').update_traces(texttemplate='%{y:.2f} %', textposition='outside').update_layout(bargap=0.2).show()
#
px.pie(df, names=colonne,title=f'Plotly : Repartition des valeurs uniques de la colonne {colonne} en pourcentage').show()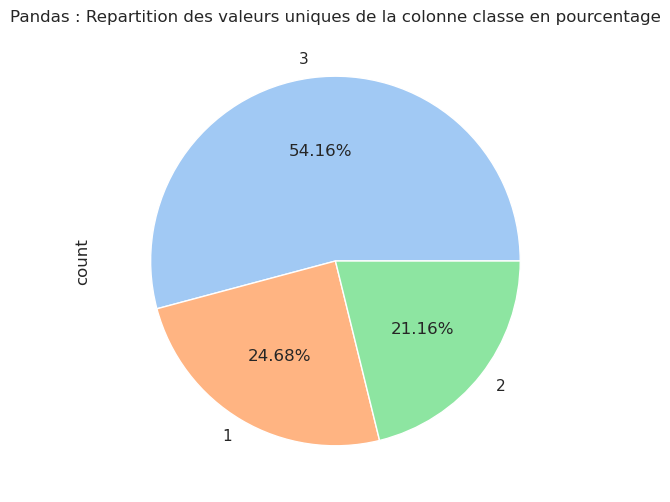

Unable to display output for mime type(s): application/vnd.plotly.v1+json

Unable to display output for mime type(s): application/vnd.plotly.v1+json

3.4 Colonne `sexe`

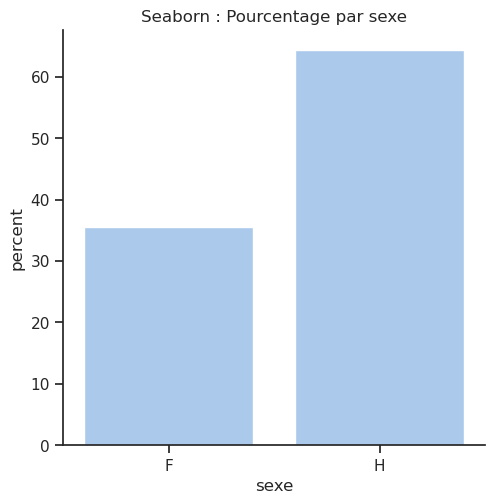
Si nécessaire, la colonne sexe peut être au préalable transformée en une colonne numérique en utilisant la méthode .replace() ou encore en utilisant la méthode .map() ou .astype().cat.codes.

# Catégorisation de la variable 'sexe' en 'sexe_code'
# ===================================================
# df['sexe_code'] = df['sexe'].astype('category').cat.codes
# df['sexe_code'] = df['sexe'].map({'H':0, 'F':1})
# df['sexe_code'] = df['sexe'].replace({'H':0, 'F':1})

# Nombre d'occurrences et pourcentage de chaque catégorie
afficher_compte_et_pourcentage(df, 'sexe')

	Nb occurrences	Pourcentage (%)
sexe
H	843	64.4
F	466	35.6

# Avec Pandas et dans un camembert
# ------------------------------
df['sexe'].value_counts().plot(kind='pie', autopct='%1.2f%%')
plt.title('Pandas : Pourcentage par sexe')
plt.show()

# Avec Seaborn
# ------------------------------
# 'catplot()': Figure-level interface for drawing categorical plots onto a FacetGrid.
# sns.catplot(x='sexe', data=df, kind='count');
sns.catplot(x='sexe', data=df, kind='count', stat='percent')
plt.title('Seaborn : Pourcentage par sexe')
plt.show()

# Avec plotly.express
# ------------------------------
# px.pie(df, names='sexe').show()
# px.histogram(df, x='sexe', text_auto=True).show()
px.pie(df, 
       names='sexe', 
       color='sexe', 
       title='Plotly : Pourcentage par sexe',
         ).update_traces( texttemplate="%{label} : %{value} (%{percent})" ,
                            textposition="outside",    # texte à l’extérieur du secteur
                            pull=[0.05]*len(df['sexe'].unique())# léger décalage pour chaque secteur
                          ).show()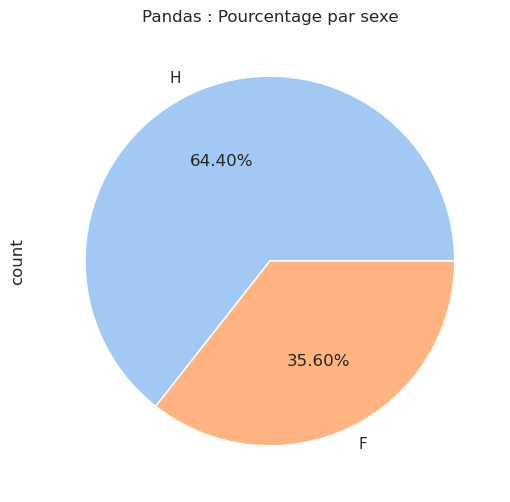

Unable to display output for mime type(s): application/vnd.plotly.v1+json

3.5 Colonne `survivant`

Selon le site Titanic Facts, 706 personnes ont survécu, dont 492 passagers et 214 membres d’équipage. Vérifions si nos données confirment cette information :

# Compte et le pourcentage de chaque catégorie

afficher_compte_et_pourcentage(df, 'survivant')

	Nb occurrences	Pourcentage (%)
survivant
0	809	61.8
1	500	38.2

Seulement environ 38 % des personnes ont survécu. Existe-t-il un moyen de savoir quels types de personnes ont eu le plus de chances de survivre ? Y a-t-il des caractéristiques particulières partagées par les survivants ? Pour répondre à ces questions, nous examinerons plus tard les autres colonnes et leurs relations avec la colonne survivant.

# Barres : matplotlib ou seaborn

# df['survivant'].value_counts().plot(kind='bar');
# sns.countplot(data=df, x='survivant');

# df['survivant'].value_counts(normalize=True).plot(kind='bar');
# sns.countplot(data=df, x='survivant', stat='percent');
# sns.countplot(data=df, x='survivant', stat='proportion');

# Pourcentage dans un camembert
# ================================================================

# Avec Pandas
# ------------------------------
df['survivant'].value_counts().plot(kind='pie', autopct='%1.2f%%')
plt.title('Pandas : Pourcentage de survivants')
plt.show()


# Avec plotly.express
# ------------------------------

# px.pie(df, names='survivant')

# Mieux : chaque secteur affiche directement le nom (1 ou 0), le nombre d’occurrences et le pourcentage.
px.pie(df, 
       names='survivant', 
       color='survivant', 
       color_discrete_sequence=px.colors.qualitative.Pastel,
       title='Plotly : Pourcentage de survivants'
       ).update_traces( texttemplate="%{label} : %{value} (%{percent})" ,
                        textposition="outside",    # texte à l’extérieur du secteur
                        pull=[0.05]*len(df['survivant'].unique())# léger décalage pour chaque secteur)
                        ).show()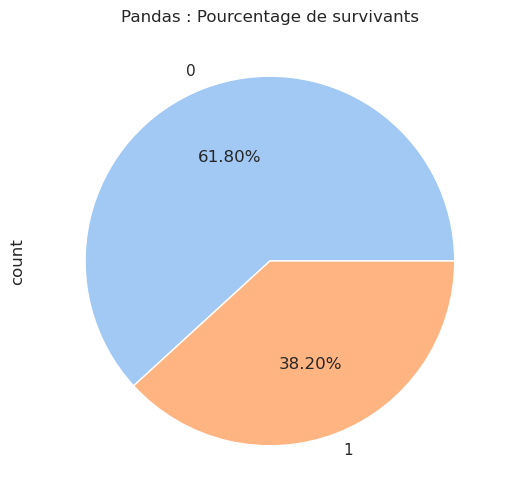

Unable to display output for mime type(s): application/vnd.plotly.v1+json

3.6 Colonne `age`

Analysons d’abord les données numériques pour la colonne de l’âge. On peut choisir de n’afficher que certaines informations (par exemple, la moyenne et l’écart-type) en utilisant la méthode .agg() :

# Statistiques descriptives pour une variable numérique
# ==================================================================

# Méthode 1 : la méthode describe()
# ----------------------------------
# df[['age']].describe()

# Méthode 2 : en choisissant les statistiques souhaitées
# ------------------------------------------------------
# df[['age']].agg(['count','mean','median','std','min','max','nunique'])

# Méthode 3 : encore mieux, en définissant une fonction pour le nombre de valeurs manquantes et l'utilisant dans agg()
# ----------------------------------------------------------------------------------------------------------------------

missing_percent = lambda x: x.isna().mean() * 100
missing_percent.__name__ = 'missing_percent'   # pour un joli nom dans le résultat

def missing(x):
    return x.isna().sum()

df[['age']].agg({
    'age': ['count', missing, missing_percent, 'mean', 'median', 'std', 'min', 'max', 'nunique']
}).rename(index={'missing': 'missing_count'}).T

	count	missing_count	missing_percent	mean	median	std	min	max	nunique
age	1046.0	263.0	20.091673	29.881135	28.0	14.4135	0.1667	80.0	98.0

Comme on peut le voir, l’âge moyen des passagers est d’environ 29,9 ans, avec un écart-type de 14,5 ans. Cependant, il manque 263 valeurs dans cette colonne, ce qui représente environ 20 % des données. Nous pourrions soit supprimer ces lignes, soit remplacer les valeurs manquantes par la moyenne de l’âge des passagers par exemple ou simplement ne pas les prendre en compte dans notre analyse. Pour le moment nous n’allons pas modifier les données.

# Boxplot pour la variable 'age' : 
# quartiles, médiane, valeurs extrêmes et outliers
# ==================================================================
sns.boxplot(x=df["age"])
plt.title("age Boxplot")
plt.show()

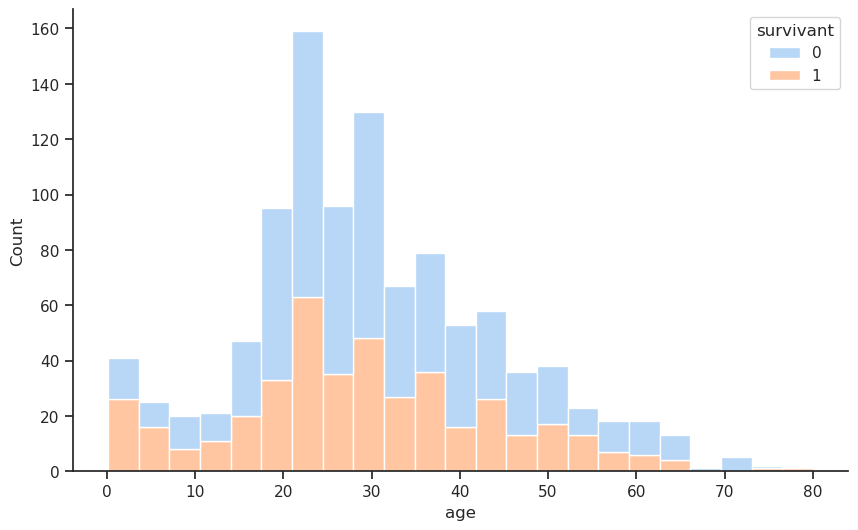
On peut afficher l’histogramme de la distribution de l’âge des passagers en utilisant le type de graphique hist de la fonction .plot() ou utiliser la fonction histplot() de Seaborn ou histogram() de Plotly Express. Dans les trois cas on peut décider de regrouper les âges par intervalles de 10 ans en utilisant l’argument bins.

On peut aussi ajouter une courbe de densité (KDE = Kernel Density Estimation) : c’est une courbe lissée qui représente la distribution d’un ensemble de données. Elle sert à visualiser la forme générale de la distribution, sans dépendre des bins de l’histogramme.

# Pandas
# ------------------------------
# Rque : Pandas n’a pas de kde=True dans plot(kind='hist'), il a une fonction KDE séparée. 
# Utiliser density=True pour que l’histogramme et le KDE soient sur la même échelle 
# Dans ce cas en ordonnée on a la densité de probabilité (somme des barres = 1) et non plus le nombre d’occurrences
df['age'].plot(kind='hist',  bins=range(0, 90), edgecolor='white', title="Histogramme avec plot, bins=range(0, 90)") #, density=True)
# df['age'].plot(kind='kde')
plt.show()

df['age'].plot(kind='hist', bins=range(0, 90, 10), edgecolor='white', title="Histogramme avec plot, bins=range(0, 90, 10)") #, density=True)
# df['age'].plot(kind='kde')
plt.show()


# Seaborn
# ------------------------------
# Rque : seaborn a kde=True dans histplot() et le rescale automatiquement
sns.histplot(data=df, x='age',  bins=range(0, 90), kde=True);
plt.title("Histogramme avec histplot de Seaborn, bins=range(0, 90)");
plt.show()

sns.histplot(df['age'], bins=range(0, 90, 10), edgecolor='white', kde=True);
plt.title("Histogramme avec histplot de Seaborn, bins=range(0, 90, 10)")
plt.show()


# Avec plotly.express
# ------------------------------
px.histogram(df, x='age', nbins=90, title='Histogramme des âges').show()

# NB Avec plotly.express, la gestion des bins est différente de matplotlib ou seaborn : 
# il faut préciser xbins pour définir les bornes des classes.
px.histogram(
    df, 
    x='age', 
    title="Histogramme Plotly : bins de 10 ans"
).update_traces( xbins=dict( start=0, end=90, size=10 ) ).update_layout(bargap=0.2).show()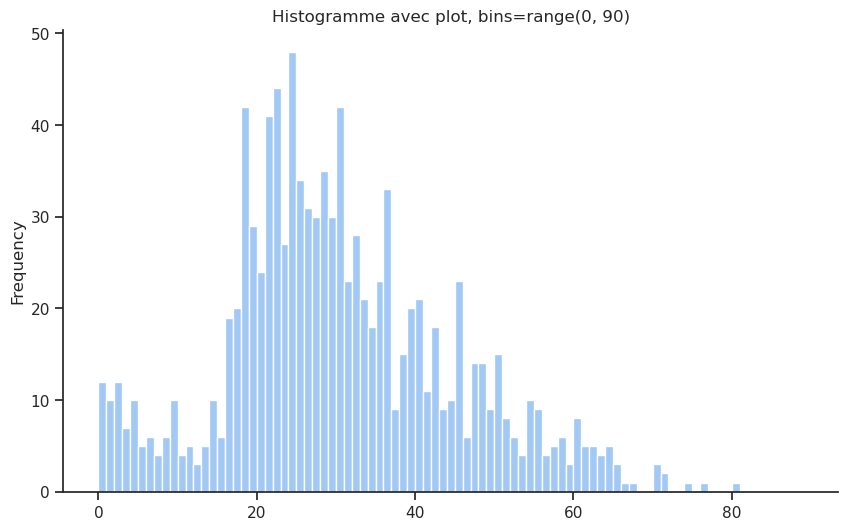

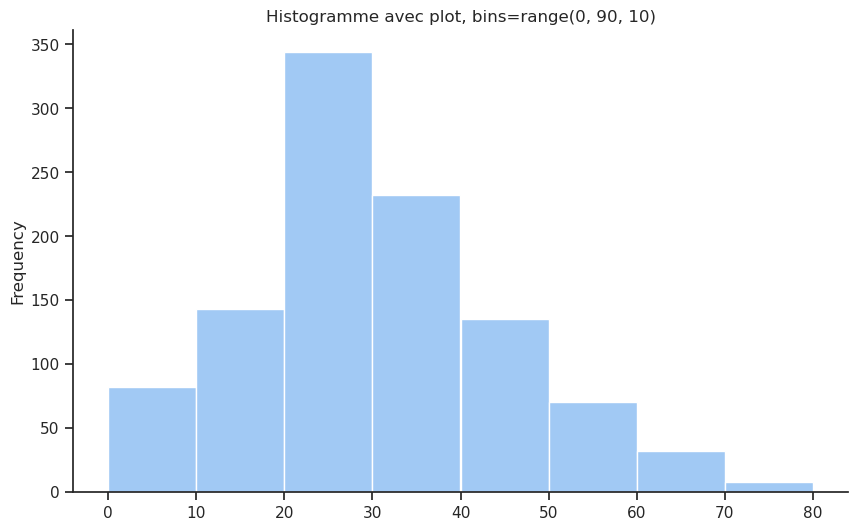
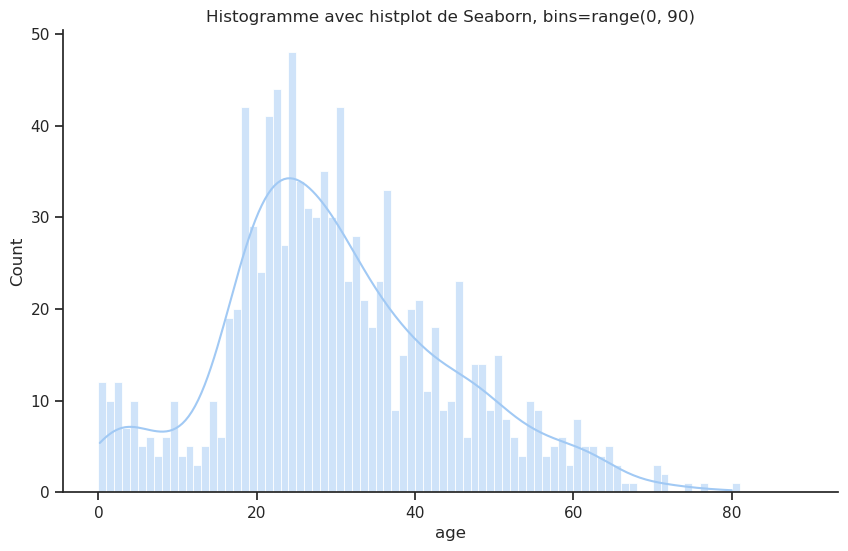
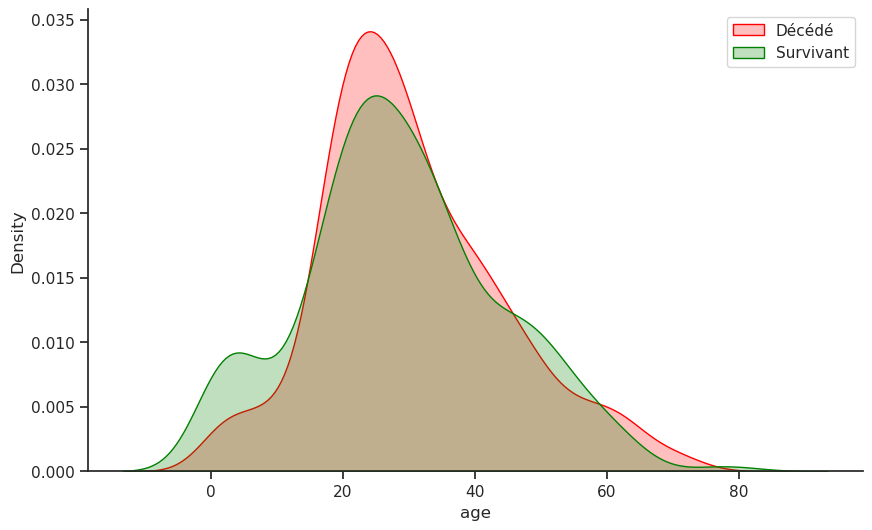
Unable to display output for mime type(s): application/vnd.plotly.v1+json

Unable to display output for mime type(s): application/vnd.plotly.v1+json

La répartition par âge est globalement en forme de cloche, avec un pic autour de la tranche d’âge 20-30 ans. Il est intéressant de noter qu’il y a un pic local vers la gauche dans la tranche d’âge 0-5 ans, ce qui indique la présence de nombreux nourrissons et enfants en bas âge à bord. D’un point de vue historique, cela est logique, car à cette époque, les voyages concernaient souvent de jeunes adultes qui commençaient une nouvelle vie, parfois accompagnés d’enfants. Pour l’analyse de survie, cela est important, car les enfants étaient souvent prioritaires lors des opérations de sauvetage.

3.7 Nouvelle Colonne `age_group`

On peut regrouper les données en découpant un ensemble de valeurs selon des intervalles, comme on l’a vu sur les graphiques précédents. Cela semble pertinent pour l’âge. On va donc ajouter une colonne age_group à notre DataFrame qui contiendra l’âge regroupé par intervalles de 10 ans. Pour cela,

on peut utiliser la méthode pd.cut() en spécifiant les valeurs à découper et les étiquettes des intervalles,
on peut passer à pd.map() une fonction que nous aurons définie pour regrouper les âges par intervalles de 10 ans.

# Première méthode
# ------------------------------

df['age_group'] = pd.cut(df['age'], bins=range(0, 90, 10), labels=[f'{i}-{i+10}' for i in range(0, 80, 10)])
df['age_group'] = df['age_group'].astype(str).replace('nan', 'Unknown')

# Deuxième méthode
# ------------------------------
# df['age_group'] = df['age'].map(lambda x: f'{int(x/10)*10}-{int(x/10)*10+10}' if not np.isnan(x) else 'Unknown')

display(df)

	classe	survivant	sexe	age	prix	port_depart	age_group
0	1	1	F	29.0000	211.3375	S	20-30
1	1	1	H	0.9167	151.5500	S	0-10
2	1	0	F	2.0000	151.5500	S	0-10
3	1	0	H	30.0000	151.5500	S	20-30
4	1	0	F	25.0000	151.5500	S	20-30
...	...	...	...	...	...	...	...
1304	3	0	F	14.5000	14.4542	C	10-20
1305	3	0	F	NaN	14.4542	C	Unknown
1306	3	0	H	26.5000	7.2250	C	20-30
1307	3	0	H	27.0000	7.2250	C	20-30
1308	3	0	H	29.0000	7.8750	S	20-30

1309 rows × 7 columns

# Nb d'occurrences et pourcentage de chaque catégorie (age_group)

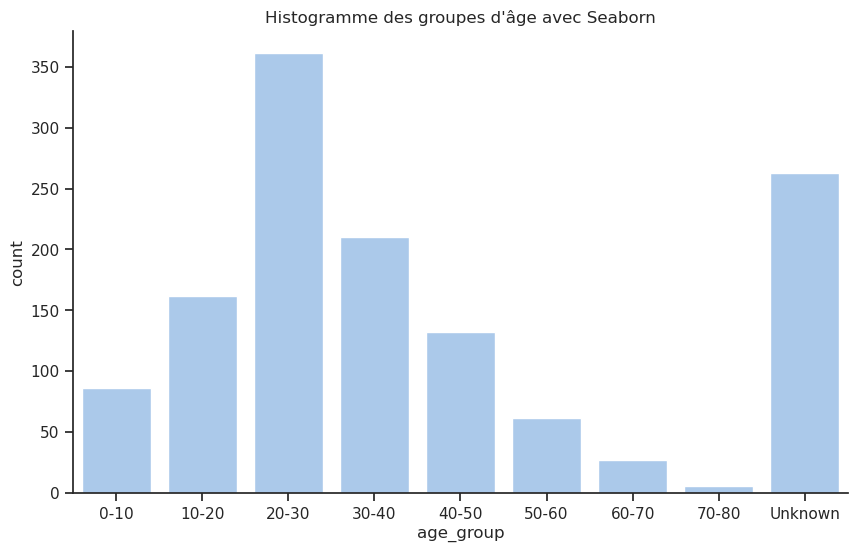
afficher_compte_et_pourcentage(df, 'age_group')

	Nb occurrences	Pourcentage (%)
age_group
20-30	361	27.58
Unknown	263	20.09
30-40	210	16.04
10-20	162	12.38
40-50	132	10.08
0-10	86	6.57
50-60	62	4.74
60-70	27	2.06
70-80	6	0.46

Histogramme des âges :

# Méthode 1 : Utiliser pandas pour créer un graphique en barres trié
# ----------------------------------------------------------------------

# df['age_group'].plot(kind='bar', edgecolor='black'); # ne fonctionne pas car les valeurs sont catégorielles
# df['age_group'].value_counts().plot(kind='bar', edgecolor='black'); # ok mais pas trié par ordre croissant
df['age_group'].value_counts().sort_index().plot(kind='bar', edgecolor='black')
plt.title("Histogramme des groupes d'âge avec plot de Pandas")
plt.show()

# Méthode 2 : Utiliser seaborn pour créer un countplot trié
# ----------------------------------------------------------------------
sns.countplot(data=df, x='age_group', order=sorted(df['age_group'].unique()));
plt.title("Histogramme des groupes d'âge avec Seaborn")
plt.show()

# Méthode 3 : Utiliser plotly.express
# ----------------------------------------------------------------------
px.histogram(df, 
             x='age_group', 
             title="Histogramme des groupes d'âge avec Plotly",
             category_orders={'age_group': sorted(df['age_group'].unique())}, text_auto=True).show()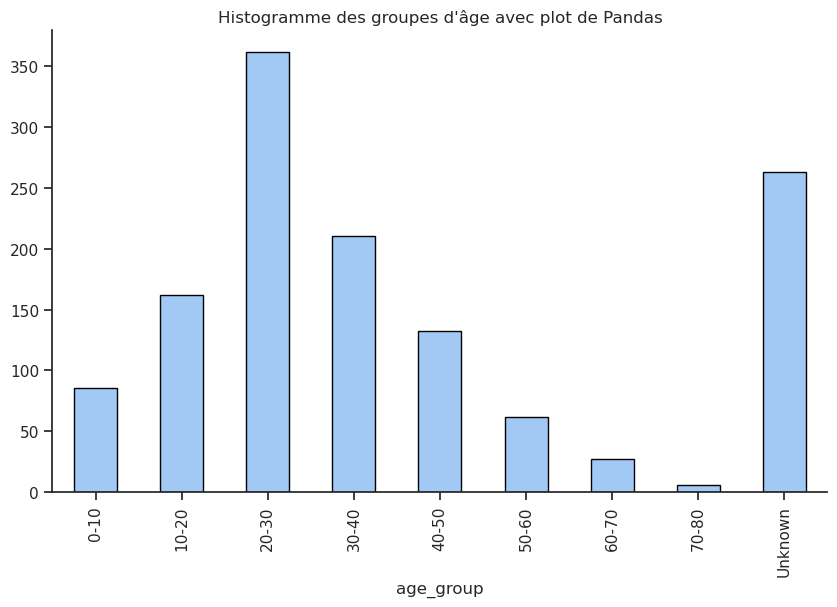

Unable to display output for mime type(s): application/vnd.plotly.v1+json

Pourcentage d’occurrences dans chaque groupe d’âge :

# Avec Pandas et dans un camembert
# ------------------------------
df['age_group'].value_counts().plot(kind='pie', 
                                    autopct='%1.2f%%', 
                                    #explode=[0.1]*len(df['age_group'].unique())
                                    )
plt.title("Pandas : Pourcentage par groupe d'âge")
plt.show()

# Avec plotly.express
# ------------------------------

# px.pie(df, names='age_group')

# Mieux 
px.pie(df, 
       names='age_group', 
       color='age_group', 
       title="Plotly : Pourcentage par groupe d'âge",
       color_discrete_sequence=px.colors.qualitative.Pastel
       ).update_traces( texttemplate="%{label} : %{value} (%{percent})" ,
                        textposition="outside",    # texte à l’extérieur du secteur
                        pull=[0.05]*len(df['age_group'].unique()))  # léger décalage pour chaque secteur)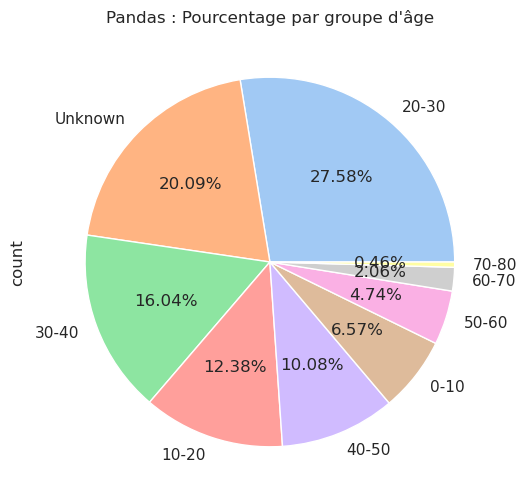

Unable to display output for mime type(s): application/vnd.plotly.v1+json

4 Liens entre deux ou plusieurs colonnes

Jusqu’à présent, nous n’avons exploré que les statistiques descriptives, mais les véritables informations apparaissent lorsque nous relions ces caractéristiques à la variable cible : survivant.
Les passagers plus jeunes ont-ils un taux de survie plus élevé ? Les passagers payant plus cher, souvent ceux de première classe, avaient-ils un meilleur accès aux canots de sauvetage ? Ce sont les questions que nous allons aborder ensuite en superposant les résultats de survie à nos distributions. Intuitivement, on pourrait s’attendre à ce que les enfants et les passagers de classe supérieure bénéficient d’un avantage en termes de survie.

Dans cette partie nous allons utiliser les méthodes suivantes :

.crosstab()
.plot(kind='bar') .plot(kind='hist') .value_counts().plot(kind='pie')
sns.countplot() sns.histplot() sns.catplot()
px.histogram() px.pie()

4.1 Analyse bivariée, vue d’ensemble

Pour une vue d’ensemble, nous pouvons utiliser la fonction pairplot() de Seaborn : elle crée une matrice de graphiques où chaque variable numérique du dataset est comparée à toutes les autres. Chaque ligne et colonne correspond à une variable. Les graphes diagonaux montrent généralement la distribution de chaque variable (histogramme ou KDE). Les graphes hors diagonale montrent la relation entre chaque paire de variables (scatter plot par défaut).

Avec ce pairplot, on peut visualiser d’un coup d’œil les patterns les plus importants comme la survie selon le sexe et la classe ou encore l’âge des survivants comparé à celui des non-survivants.

df['sexe_num'] = df['sexe'].astype('category').cat.codes
# df['port_depart_num'] = df['port_depart'].astype('category').cat.codes

# Sélection des variables numériques et catégorielles codées
# ==========================================================
pairplot_vars = ['age', 'prix', 'classe', 'sexe_num']



# Avec Seaborn
# ------------------------------

g = sns.pairplot(
    data=df[pairplot_vars + ['survivant']],  # inclure la variable cible
    hue='survivant',                         # couleur selon survie
    palette={0: 'red', 1: 'green'},          # couleurs personnalisées
    diag_kind='kde',                         # KDE pour la diagonale
    markers=['o', 's'],                      # forme différente selon la classe
    plot_kws={'alpha':0.6, 's':50}           # transparence et taille des points
)
# Ajuster les légendes
# for t, l in zip(g._legend.texts, ["Décédé", "Survécu"]):
#     t.set_text(l)
plt.title('Avec Seaborn')
plt.show()


# Avec plotly.express
# ------------------------------
# fig = px.scatter_matrix(
#     df,
#     dimensions=pairplot_vars,  # variables à afficher
#     color=df['survivant'].map({0: 'Décédé', 1: 'Survécu'}),
#     color_discrete_map={'Décédé': 'red', 'Survécu': 'green'},
#     symbol='survivant',  # forme différente selon la classe
#     symbol_map={0: 'circle', 1: 'square'},
#     opacity=0.6,  # transparence
#     height=800,   # hauteur de la figure
#     title='Avec Plotly'
# )
# fig.update_traces(
#     marker=dict(size=5),       # taille des points
#     diagonal_visible=False     # masquer la diagonale (pas de KDE natif))
# )
# fig.update_layout(width=1000, height=1000)
# fig.show()

Caveat

Le paradoxe de Simpson : la difficulté de comparer des pourcentages

L’étude des relations entre 3 ou plus caractéristiques (par exemple sexe, classe et survie), peut être délicat. En effet, il existe un phénomène statistique contre-intuitif appelé paradoxe de Simpson.
Ce paradoxe se produit lorsqu’une tendance observée dans chaque sous-groupe disparaît ou s’inverse lorsque l’on regroupe les données.
Ainsi, les pourcentages globaux peuvent raconter une histoire différente (et parfois totalement fausse) de celle révélée par les sous-groupes.

Exemple illustratif : l’inversion des pourcentages

Considérons deux médicaments (A et B) testés sur des hommes et des femmes. Les tableaux suivants indiquent le nombre de personnes traitées et le nombre de guérisons.

	Médicament A		Médicament B
Genre	Total	Guéris	Total	Guéris
Hommes	5	1	10	3
Femmes	9	4	2	1

Taux de guérison

Groupe	Médicament A	Médicament B
Hommes	\(1/5=20\%\)	\(3/10=30\%\)
Femmes	\(4/9=44\%\)	\(1/2=50\%\)
Total	\(5/14=36\%\)	\(4/12=33\%\)

Conclusion :

chez les hommes, le médicament B guérit davantage que A ;
chez les femmes, le médicament B guérit encore davantage que A ;
mais une fois les deux groupes combinés, le médicament A apparaît meilleur que B.

Le classement s’inverse au niveau global : c’est le paradoxe de Simpson. Le renversement provient de la répartition très inégale des tailles de groupes. Mathématiquement, le paradoxe vient du fait que les inégalités

\[ \frac{a}{b}<\frac{A}{B} \quad\text{et}\quad \frac{c}{d}<\frac{C}{D} \]

n’impliquent pas que

\[ \frac{a+c}{b+d}<\frac{A+C}{B+D}. \]

Dans la suite, il faudra faire très attention à comparer uniquement les pourcentages globaux de survivants par catégorie d’une autre variable si les distributions des sous-groupes sont très différentes.

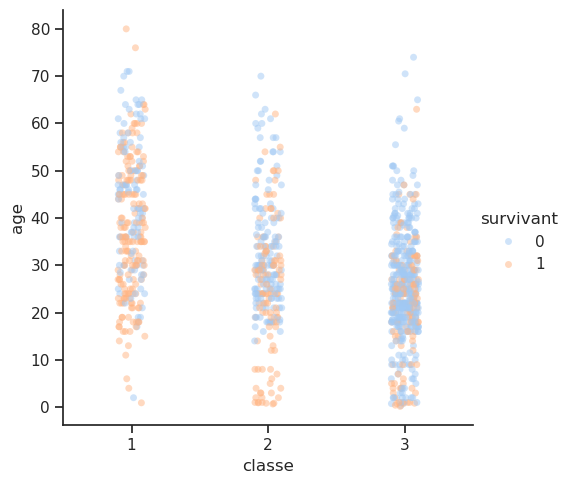
4.2 Classe / Survie

Observons la colonne classe.
Il y a trois catégories dans cette colonne : les passagers de 1re classe, de 2e classe et de 3e classe représentés respectivement par les chiffres 1, 2 et 3.
Est-ce que les passagers de 1re classe ont eu la priorité pour monter à bord du navire et peut-être la priorité pour être sauvés dans les canots de sauvetage ? Autrement-dit, est-ce que les passagers de 1re classe ont un taux de survie plus élevé par rapport à ceux de 2e ou 3e classe ? Vérifions si c’est le cas.

La méthode .crosstab() permet de créer un tableau de contingence pour voir combien de personnes de chaque classe ont survécu ou non.

pd.crosstab(df['classe'], df['survivant'], margins=True, margins_name='Total')

survivant	0	1	Total
classe
1	123	200	323
2	158	119	277
3	528	181	709
Total	809	500	1309

Même résultat avec .pivot_table() : la fonction size compte le nombre d’occurrences dans chaque groupe et fill_value=0 remplace les NaN par 0 (utile si certaines combinaisons de valeurs n’existent pas). La fonction pivot_table() ne propose pas de manière directe pour ajouter des marges comme crosstab(), il faut donc additionner les marges séparément.

pt = df.pivot_table(index='classe', columns='survivant', aggfunc='size', fill_value=0)
pt['Total'] = pt.sum(axis=1)  # Total par ligne
pt.loc['Total'] = pt.sum(axis=0)  # Total par colonne
pt

survivant	0	1	Total
classe
1	123	200	323
2	158	119	277
3	528	181	709
Total	809	500	1309

On peut également afficher le pourcentage de survie pour chaque classe, mais il faut choisir entre 3 options :

le pourcentage de survivants dans chaque classe
la répartition de chaque classe parmi les survivants/non-survivants
le pourcentage de couple (classe, survie) parmi le total

# Nomenclature :
# --------------------------
# tc = tableau croisé
# cl_sur = classe survivant
# norm = normalizé

# Pourcentage par ligne
display(Markdown("**Pourcentage par ligne : combien de survivants parmi chaque classe**"))
tc_cl_sur_norm_lignes= pd.crosstab(df['classe'], df['survivant'], margins=True, margins_name='Total', normalize='index')
display(tc_cl_sur_norm_lignes)

# Pourcentage par colonne
display(Markdown("**Pourcentage par colonne : proportion de chaque classe parmi les survivants et les non survivants**"))
tc_cl_sur_norm_colonnes = pd.crosstab(df['classe'], df['survivant'], margins=True, margins_name='Total', normalize='columns') 
display(tc_cl_sur_norm_colonnes)

# Pourcentage total
display(Markdown("**Pourcentage total : proportion de chaque combinaison classe-survivant par rapport à l'ensemble des passagers**"))
tc_cl_sur_norm_all = pd.crosstab(df['classe'], df['survivant'], margins=True, margins_name='Total', normalize='all')
display(tc_cl_sur_norm_all)

Pourcentage par ligne : combien de survivants parmi chaque classe

survivant	0	1
classe
1	0.380805	0.619195
2	0.570397	0.429603
3	0.744711	0.255289
Total	0.618029	0.381971

Pourcentage par colonne : proportion de chaque classe parmi les survivants et les non survivants

survivant	0	1	Total
classe
1	0.152040	0.400	0.246753
2	0.195303	0.238	0.211612
3	0.652658	0.362	0.541635

Pourcentage total : proportion de chaque combinaison classe-survivant par rapport à l’ensemble des passagers

survivant	0	1	Total
classe
1	0.093965	0.152788	0.246753
2	0.120703	0.090909	0.211612
3	0.403361	0.138273	0.541635
Total	0.618029	0.381971	1.000000

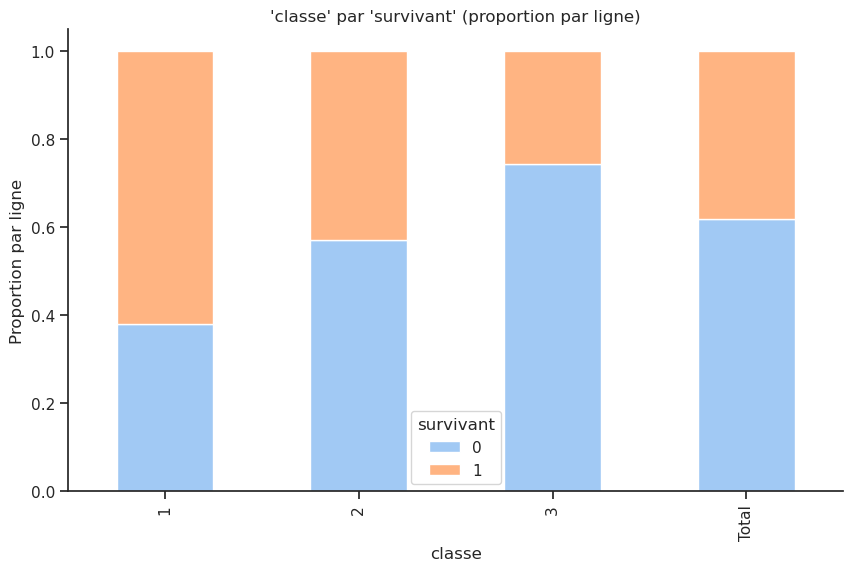
Le tableau “par ligne” indique que les passagers de 1re classe avaient un taux de survie d’environ 62 %, tandis que ceux de 2e classe avaient un taux de survie d’environ 43 %, et ceux de 3e classe seulement environ 26 %. Cela confirme l’idée que les passagers de première classe avaient un avantage significatif en termes de survie par rapport aux autres classes.

Le tableau “par colonne” montre que parmi les survivants, une proportion plus élevée venait de la 1re classe (40 %), suivi de la 3e classe (36 %) et enfin de la 2e classe (24 %). La difficulté avec ce tableau est qu’il est influencé par la répartition initiale des passagers dans chaque classe (cf. paradoxe de Simpson).

Le tableau “total” montre la répartition globale des passagers par classe, indépendamment de leur survie. Cela donne une idée aussi de la composition initiale des passagers à bord du Titanic.

On peut ensuite afficher ces informations sous forme de graphique :

# Avec Pandas et dans un graphique en barres empilées
# --------------------------------------------------------------
tc_cl_sur_norm_lignes.plot(kind='bar', stacked=True, title='Pourcentage par ligne : proportion de survivants dans chaque classe');

# NB Normalisation par ligne : chaque barre a la même hauteur (1 ou 100%) 
# et les segments représentent la proportion de survivants dans chaque classe.

# On ne peut pas faire cela avec plotly.express directement.

# Pourcentage total sans les marges
tc_cl_sur_norm_all = pd.crosstab(df['classe'], df['survivant'], normalize='all')
display(tc_cl_sur_norm_all)
tc_cl_sur_norm_all.plot(kind='bar', stacked=True, title='Pourcentage total : proportion de chaque combinaison classe-survivant par rapport à l\'ensemble des passagers');

survivant	0	1
classe
1	0.093965	0.152788
2	0.120703	0.090909
3	0.403361	0.138273

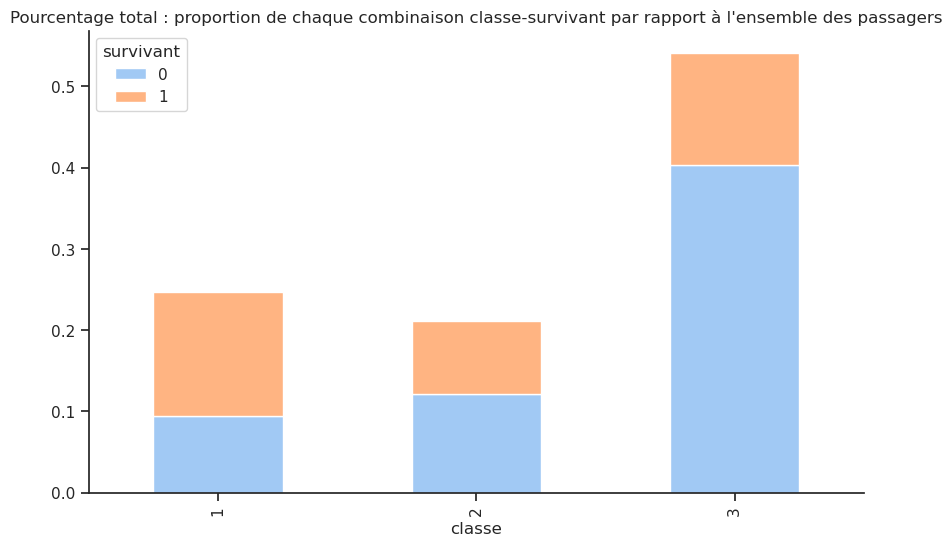
Quel graphe est le plus pertinent pour comparer les survivants et les non-survivants en fonction de la classe ?

# Quel graphe est le plus pertinent pour comparer les survivants et les non-survivants en fonction de la classe ?
# ===============================================================================================================

# sns.countplot(data=df, x='survivant')

# plt.figure();
# Chaque statut (survivant / décédé) est divisé en trois barres (classe 1, 2, 3)
sns.countplot(data=df, x='survivant', hue='classe');

plt.figure();
# Chaque classe est divisée en deux barres (survivant et non-survivant)
sns.countplot(data=df, x='classe', hue='survivant');

# plt.figure();
# sns.histplot(data=df, x='classe', hue='survivant', multiple='stack'); # idem empilées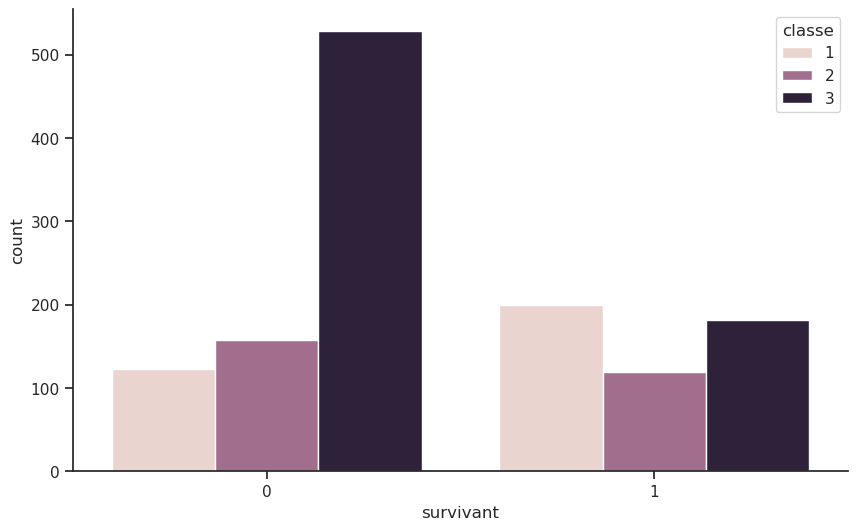

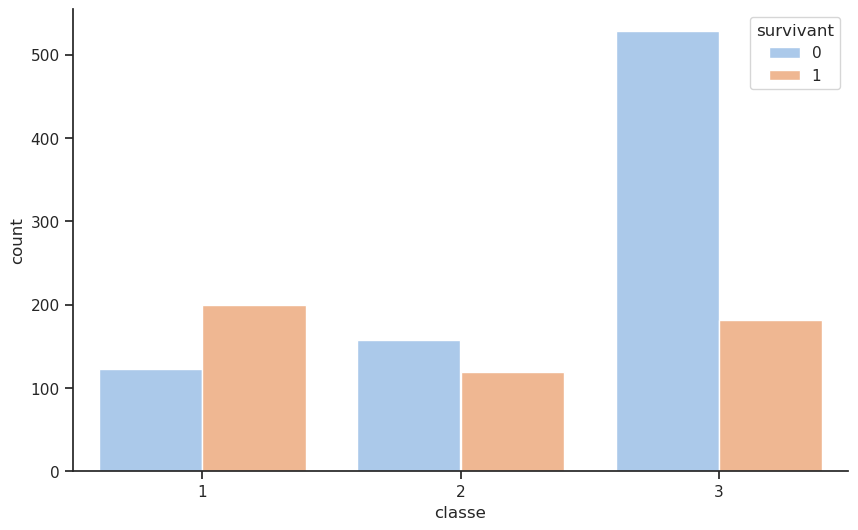
px.histogram(df, x='survivant', color='classe', barmode='group', text_auto=True).show()

px.histogram(df, x='classe', color='survivant', barmode='group', text_auto=True).show()

Unable to display output for mime type(s): application/vnd.plotly.v1+json

Unable to display output for mime type(s): application/vnd.plotly.v1+json

# Taille de la figure et disposition
rows, cols = 2, 2
fig, axx = plt.subplots(rows, cols, figsize=(14, 10))
axx = axx.flatten()  # Pour accéder facilement aux axes

# Proportion par classe
sns.countplot(data=df, x='classe', stat='proportion', ax=axx[0])
axx[0].grid()

# Proportion par survivant
sns.countplot(data=df, x='survivant', stat='proportion', ax=axx[1])
axx[1].grid()

# Classe par survivant
sns.countplot(data=df, x='classe', hue='survivant', stat='proportion', ax=axx[2])
# sns.histplot(data=df, x='classe', hue='survivant', stat='proportion', multiple='stack', ax=axx[2])
axx[2].grid()

# Survivant par classe
sns.countplot(data=df, x='survivant', hue='classe', stat='proportion', ax=axx[3])
# sns.histplot(data=df, x='survivant', hue='classe', stat='proportion', multiple='stack', ax=axx[3])
axx[3].grid()



# Ajuster l'espacement
plt.tight_layout()
plt.show()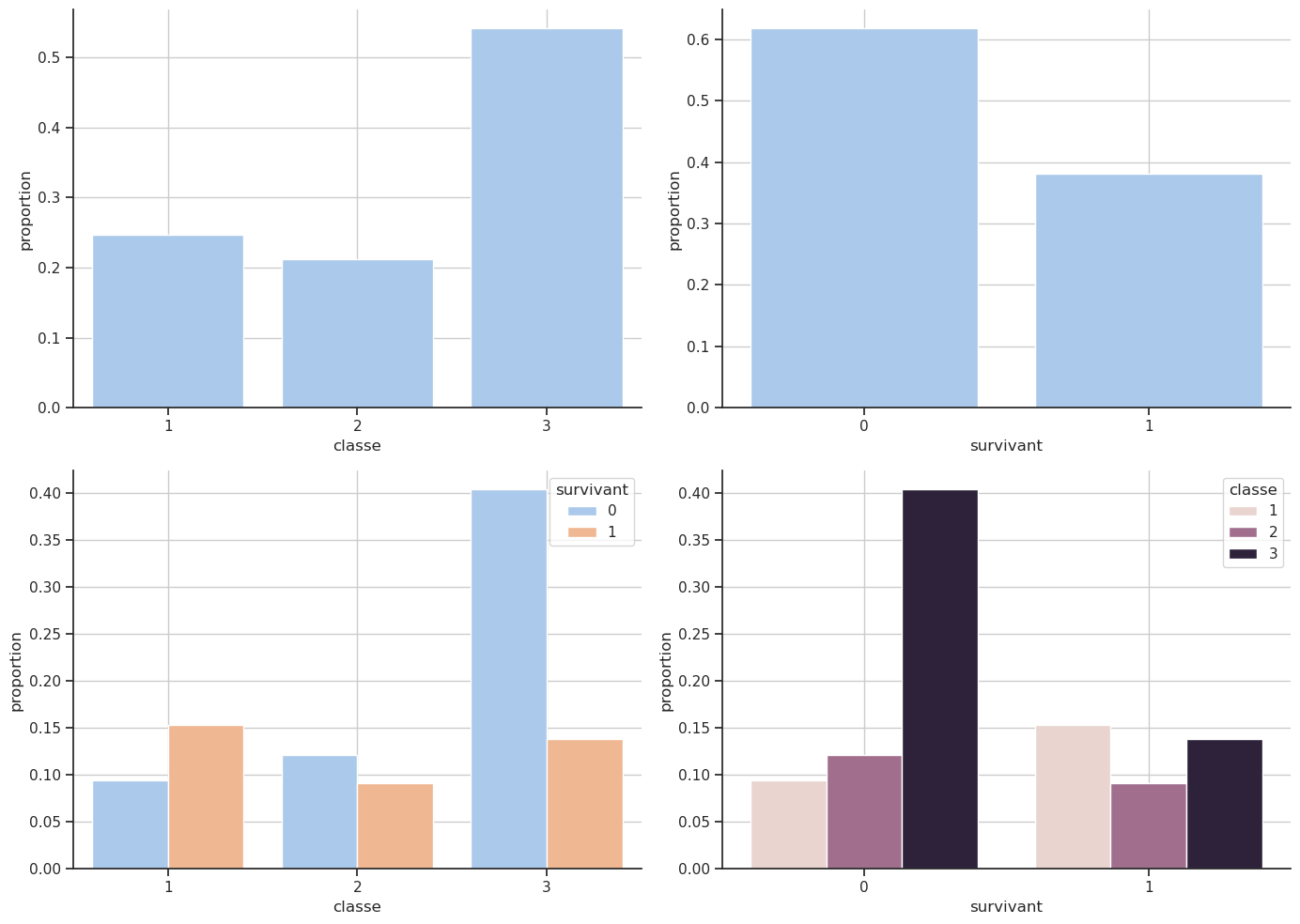

# import plotly.graph_objects as go

# fig = make_subplots(
#     rows=2, cols=2,
#     subplot_titles=(
#         "Proportion par classe",
#         "Proportion par survivant",
#         "Classe par survivant",
#         "Survivant par classe",
#     )
# )

# # Proportion par classe
# tc_cl = df['classe'].value_counts().sort_index()
# tc_cl_norm = tc_cl / tc_cl.sum()
# fig.add_trace(go.Bar(
#     x=tc_cl.index,
#     y=tc_cl_norm.values,
#     text=[f"{label}: {val} ({pct:.2%})" for label, val, pct in zip(tc_cl.index, tc_cl.values, tc_cl_norm.values)],
#     textposition="inside",
#     showlegend=False
# ), row=1, col=1)

# # Proportion par survivant
# tc_surv = df['survivant'].value_counts().sort_index()
# tc_surv_norm = tc_surv / tc_surv.sum()
# fig.add_trace(go.Bar(
#     x=tc_surv.index,
#     y=tc_surv_norm.values,
#     text=[f"{label}: {val} ({pct:.2%})" for label, val, pct in zip(tc_surv.index, tc_surv.values, tc_surv_norm.values)],
#     textposition="inside",
#     showlegend=False
# ), row=1, col=2)

# # Classe par survivant (empilé)
# tc_cl_surv = pd.crosstab(df['classe'], df['survivant'])
# tc_cl_surv_norm = tc_cl_surv.div(tc_cl_surv.sum(axis=1), axis=0)
# for col in tc_cl_surv.columns:
#     fig.add_trace(go.Bar(
#         x=tc_cl_surv.index,
#         y=tc_cl_surv_norm[col],
#         text=[f"{col}: {val} ({pct:.2%})" for val, pct in zip(tc_cl_surv[col], tc_cl_surv_norm[col])],
#         textposition="inside",
#         showlegend=False
#     ), row=2, col=1)

# # Survivant par classe (empilé)
# tc_surv_cl = pd.crosstab(df['survivant'], df['classe'])
# tc_surv_cl_norm = tc_surv_cl.div(tc_surv_cl.sum(axis=1), axis=0)
# for col in tc_surv_cl.columns:
#     fig.add_trace(go.Bar(
#         x=tc_surv_cl.index,
#         y=tc_surv_cl_norm[col],
#         text=[f"{col}: {val} ({pct:.2%})" for val, pct in zip(tc_surv_cl[col], tc_surv_cl_norm[col])],
#         textposition="inside",
#         showlegend=False
#     ), row=2, col=2)

# fig.update_layout(
#     height=800,
#     width=1000,
#     barmode='stack'
# )

# fig.show()

Nous allons généraliser cette approche en créant une fonction qui prend en argument une colonne et affiche le taux de survie pour chaque catégorie unique dans cette colonne, ainsi que les deux tableaux de contingence.

def plot_proportions(df, col1, col2):
    plt.figure(figsize=(14, 10))
    
    # Pie chart col1
    plt.subplot(2, 2, 1)
    df[col1].value_counts(normalize=True).plot(
        kind='pie', autopct='%1.2f%%', startangle=90, legend=False
    )
    plt.title(f"Répartition de '{col1}'")
    
    # Pie chart col2
    plt.subplot(2, 2, 2)
    df[col2].value_counts(normalize=True).plot(
        kind='pie', autopct='%1.2f%%', startangle=90, legend=False
    )
    plt.title(f"Répartition de '{col2}'")
    
    # Bar plot col2 par col1 (proportion)
    plt.subplot(2, 2, 3)
    sns.countplot(data=df, x=col2, hue=col1, stat='proportion')
    plt.title(f"'{col2}' par '{col1}'")
    
    # Bar plot col1 par col2 (proportion)
    plt.subplot(2, 2, 4)
    sns.countplot(data=df, x=col1, hue=col2, stat='proportion')
    plt.title(f"'{col1}' par '{col2}'")
    
    plt.tight_layout()
    plt.show()

    # Crosstabs
    tc = pd.crosstab(df[col1], df[col2], margins=True, margins_name='Total') # pourcentage total
    tc_norm = pd.crosstab(df[col1], df[col2], margins=True, margins_name='Total', normalize='index') # pourcentage par ligne
    # tc_norm_all = pd.crosstab(df[col1], df[col2], margins=True, normalize='all') # pourcentage total

    display(Markdown("Crosstab absolu :"))
    display(tc)
    display(Markdown("Crosstab normalisé par ligne :"))
    display(tc_norm)
    
    # Bar plot empilé du crosstab normalisé
    tc_norm.plot(kind='bar', stacked=True)
    plt.ylabel("Proportion par ligne")
    plt.title(f"'{col1}' par '{col2}' (proportion par ligne)")
    plt.show()


# TEST
plot_proportions(df, 'classe', 'survivant')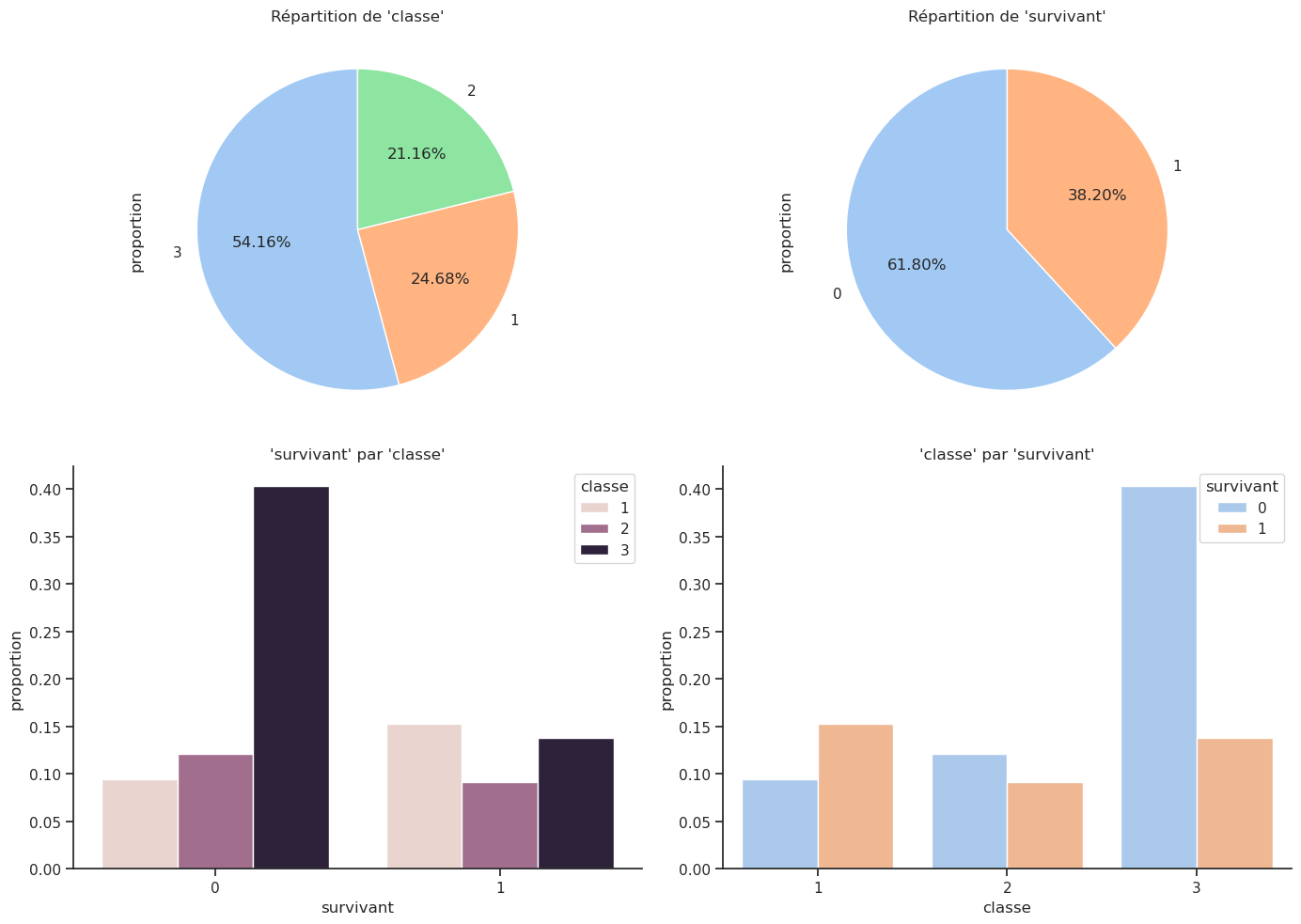

Crosstab absolu :

survivant	0	1	Total
classe
1	123	200	323
2	158	119	277
3	528	181	709
Total	809	500	1309

Crosstab normalisé par ligne :

survivant	0	1
classe
1	0.380805	0.619195
2	0.570397	0.429603
3	0.744711	0.255289
Total	0.618029	0.381971

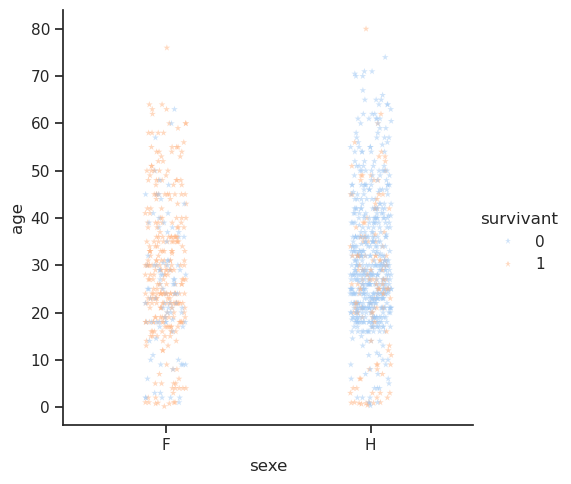
4.3 Sexe / Survie

Nous menons une enquête similaire pour la colonne sexe. L’article de Wikipédia sur le RMS Titanic indiquait que « le protocole “les femmes et les enfants d’abord” était généralement suivi lors du chargement des canots de sauvetage ». Nous pouvions donc nous attendre à un taux de survie plus élevé pour les femmes et les enfants. Vérifions si cela est vrai.

Taux de survie par sexe.

# Avec groupby
# ----------------------------------------------
display( df.groupby('sexe')['survivant'].mean() )  # proportion de survivants par sexe

# Avec crosstab
# ----------------------------------------------
sex_survivant = pd.crosstab(df['sexe'],
            df['survivant'],
            # normalize='index'
            # normalize='columns'
            # normalize='all'
            )
display(sex_survivant)

# Affichage avec Pandas
# ----------------------------------------------
sex_survivant.plot(kind='bar', stacked=True)
plt.show()

# Avec plotly.express
# ----------------------------------------------
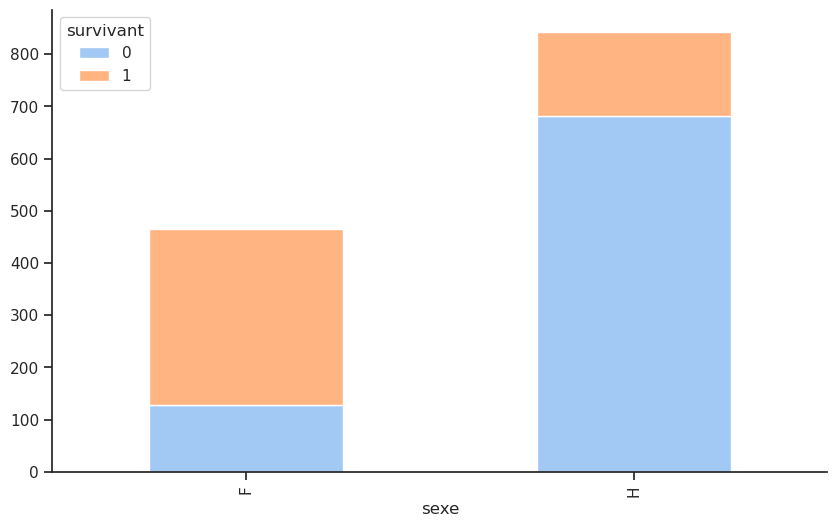
px.bar(sex_survivant, barmode='stack', text_auto=True).show()

sexe
F    0.727468
H    0.190985
Name: survivant, dtype: float64

survivant	0	1
sexe
F	127	339
H	682	161

Unable to display output for mime type(s): application/vnd.plotly.v1+json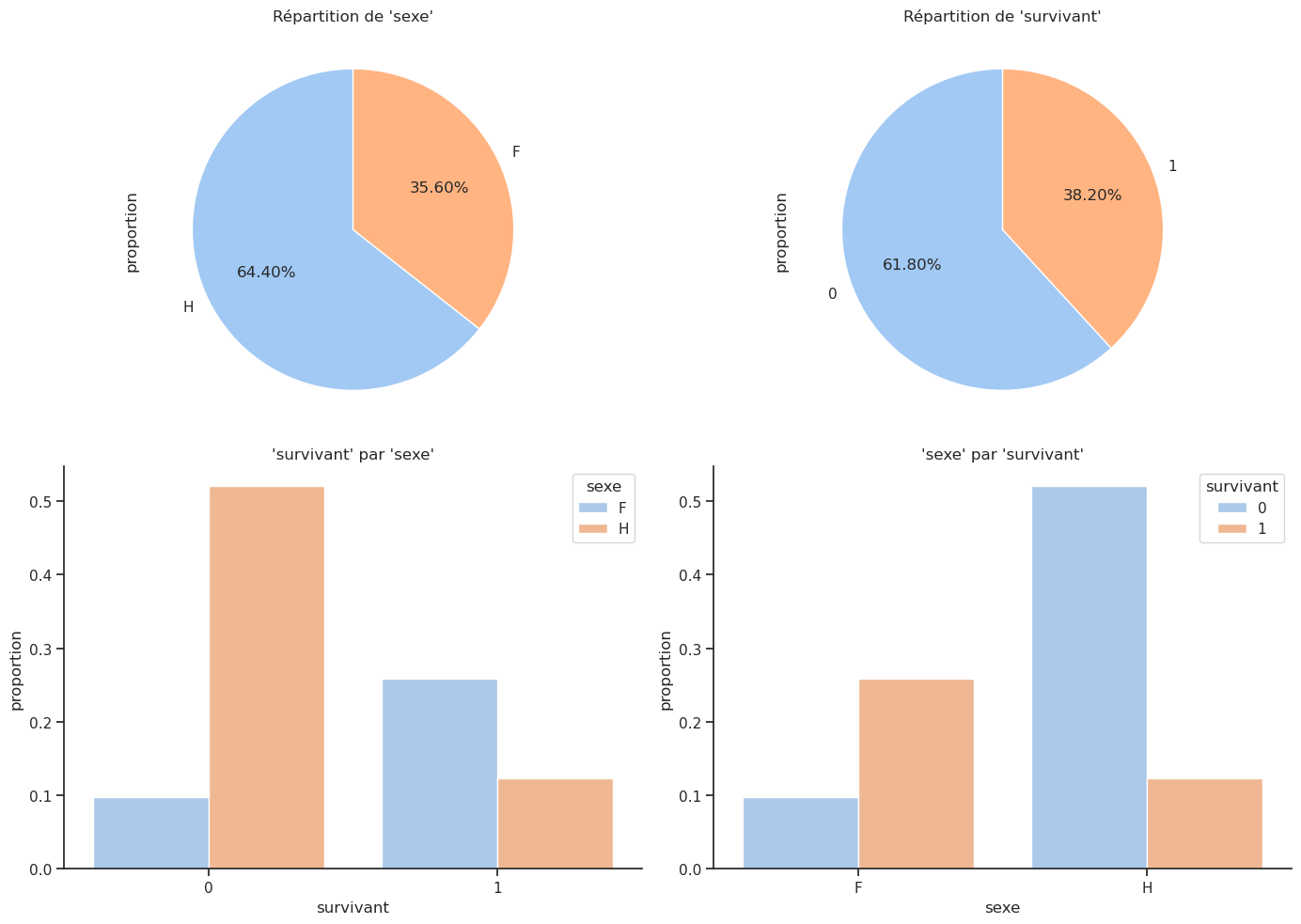

plot_proportions(df, 'sexe', 'survivant')

Crosstab absolu :

survivant	0	1	Total
sexe
F	127	339	466
H	682	161	843
Total	809	500	1309

Crosstab normalisé par ligne :

survivant	0	1
sexe
F	0.272532	0.727468
H	0.809015	0.190985
Total	0.618029	0.381971

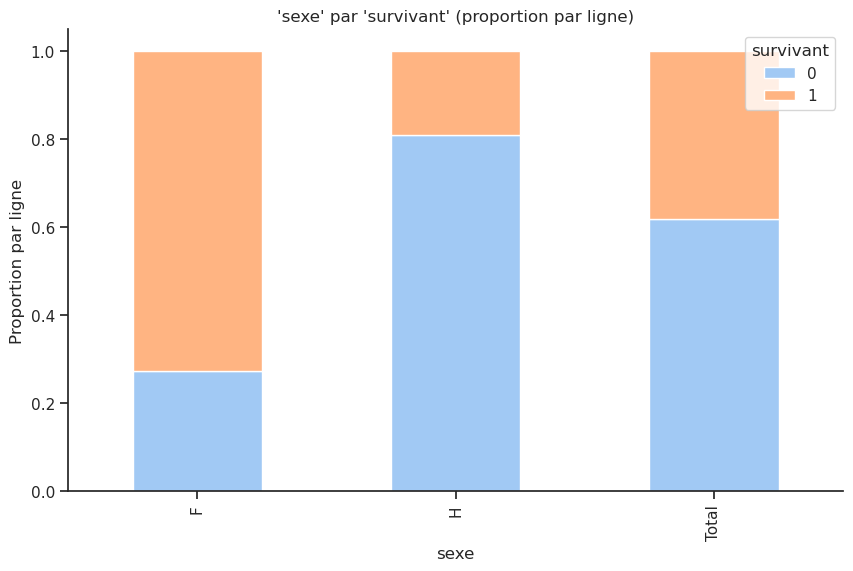
Parmi les femmes, la majorité a survécu, avec un taux de survie de 75 %, contre un taux de survie de 20 % pour les hommes.

Notons que le résultat obtenu avec crosstab() peut s’obtenir avec des masques.

Par exemple, parmi les survivants, combien étaient des hommes et combien étaient des femmes ? Le tableau précédent indique que sur les 500 survivants, 339 étaient des femmes et 161 des hommes. Voici comment faire avec une masque :

mask = (df['survivant'] == 1)
df[mask]['sexe'].value_counts()
# df[mask]['sexe'].value_counts().plot(kind='bar') ;

sexe
F    339
H    161
Name: count, dtype: int64

4.4 Age / Survie

sns.boxplot(data=df, x="survivant", y="age", showmeans=True)
plt.title("Age Distribution vs Survival")
plt.show()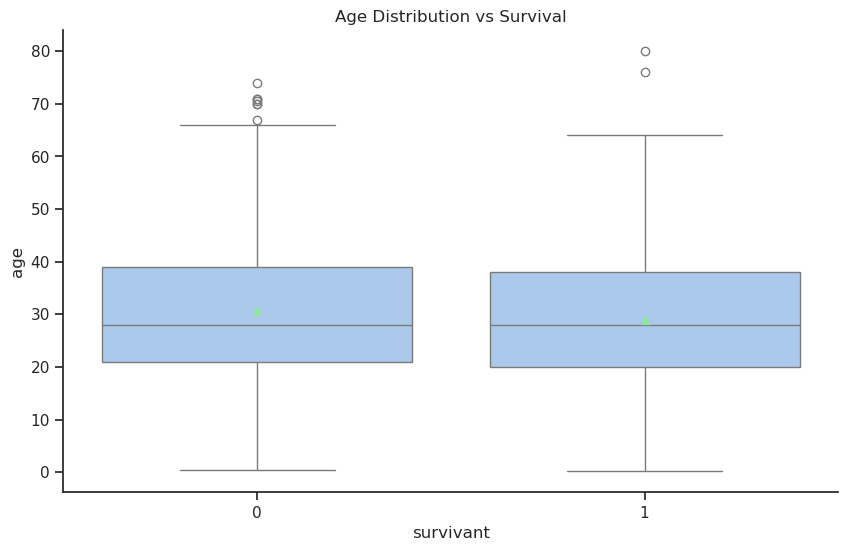

sns.kdeplot(df[df['survivant']==0]['age'].dropna(), fill=True, alpha=0.25, label='Décédé', color='red')
sns.kdeplot(df[df['survivant']==1]['age'].dropna(), fill=True, alpha=0.25, label='Survivant', color='green')
plt.legend();

sns.histplot(data=df, x="age", hue="survivant", multiple="stack");

4.5 Age_group / Survie

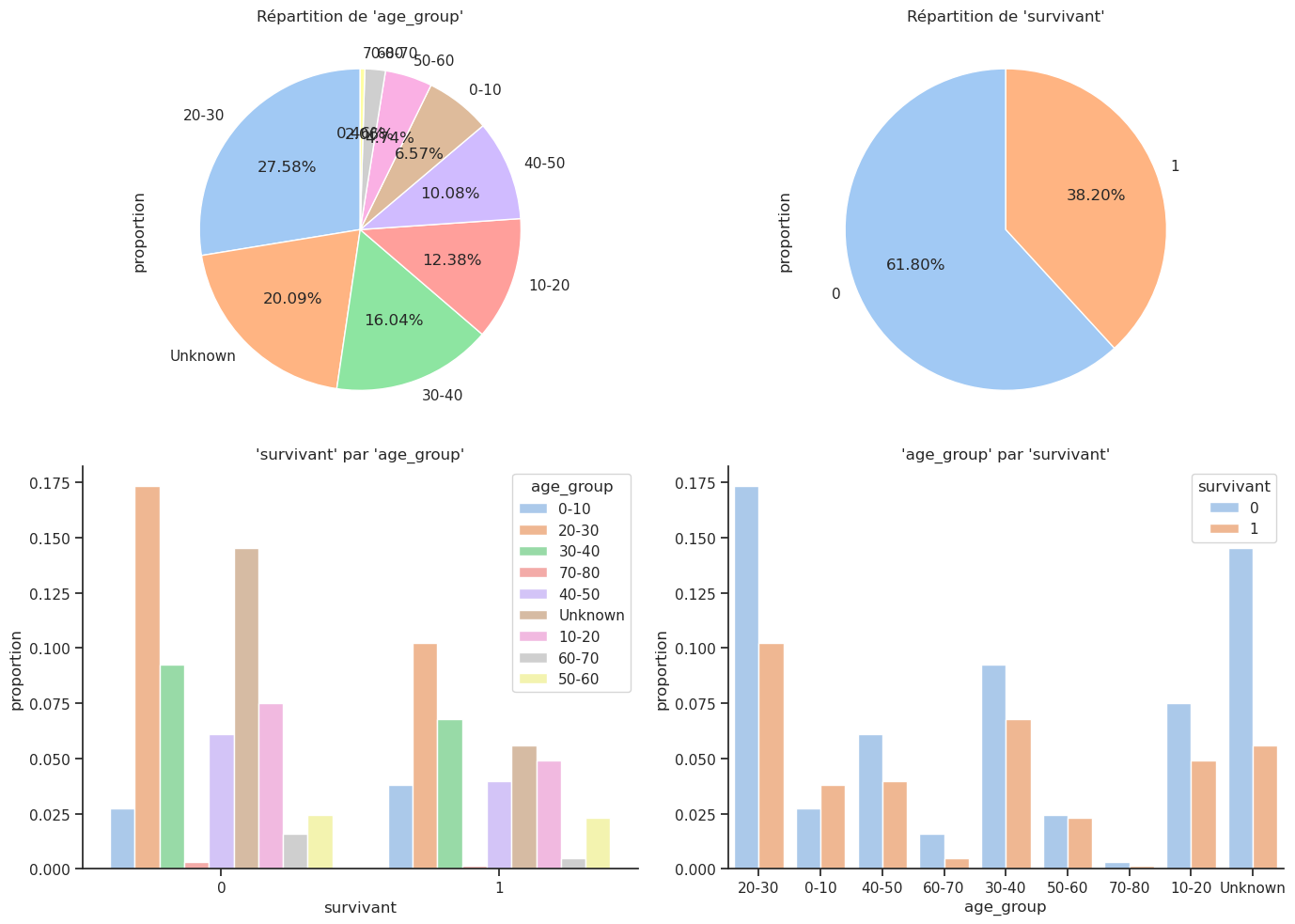
plot_proportions(df, 'age_group', 'survivant')

Crosstab absolu :

survivant	0	1	Total
age_group
0-10	36	50	86
10-20	98	64	162
20-30	227	134	361
30-40	121	89	210
40-50	80	52	132
50-60	32	30	62
60-70	21	6	27
70-80	4	2	6
Unknown	190	73	263
Total	809	500	1309

Crosstab normalisé par ligne :

survivant	0	1
age_group
0-10	0.418605	0.581395
10-20	0.604938	0.395062
20-30	0.628809	0.371191
30-40	0.576190	0.423810
40-50	0.606061	0.393939
50-60	0.516129	0.483871
60-70	0.777778	0.222222
70-80	0.666667	0.333333
Unknown	0.722433	0.277567
Total	0.618029	0.381971

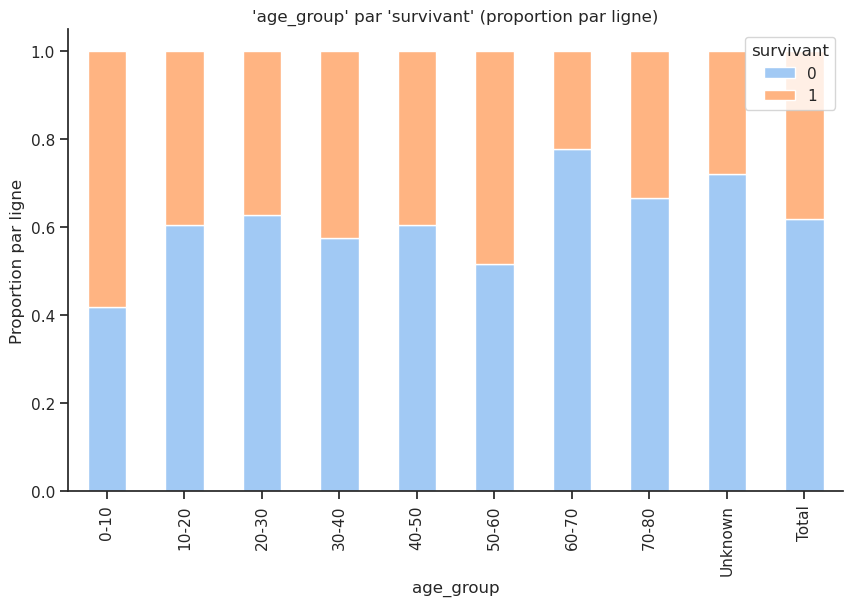
sns.histplot(data=df, x="age_group", hue="survivant", multiple="stack");

Taux de survie par âge.

# observed=False pour inclure les catégories sans valeurs
df.groupby('age_group', observed=False)['survivant'].mean()
# df.groupby('age_group', observed=False)['survivant'].mean().plot(kind='bar', edgecolor='black');

age_group
0-10       0.581395
10-20      0.395062
20-30      0.371191
30-40      0.423810
40-50      0.393939
50-60      0.483871
60-70      0.222222
70-80      0.333333
Unknown    0.277567
Name: survivant, dtype: float64

Plus de la moitié des moins de 10 ans ont survécu.

4.6 Port de départ / Survie

La dernière caractéristique catégorique que nous pouvons examiner est le port d’embarquement. Les passagers ont embarqué depuis trois ports différents nommés Cherbourg, Queenstown et Southampton, abrégés respectivement par les lettres C, Q et S. Nous avons déjà vu que le sexe et la classe influencent le taux de survie des passagers. Le port d’embarquement influence-t-il la survie ?

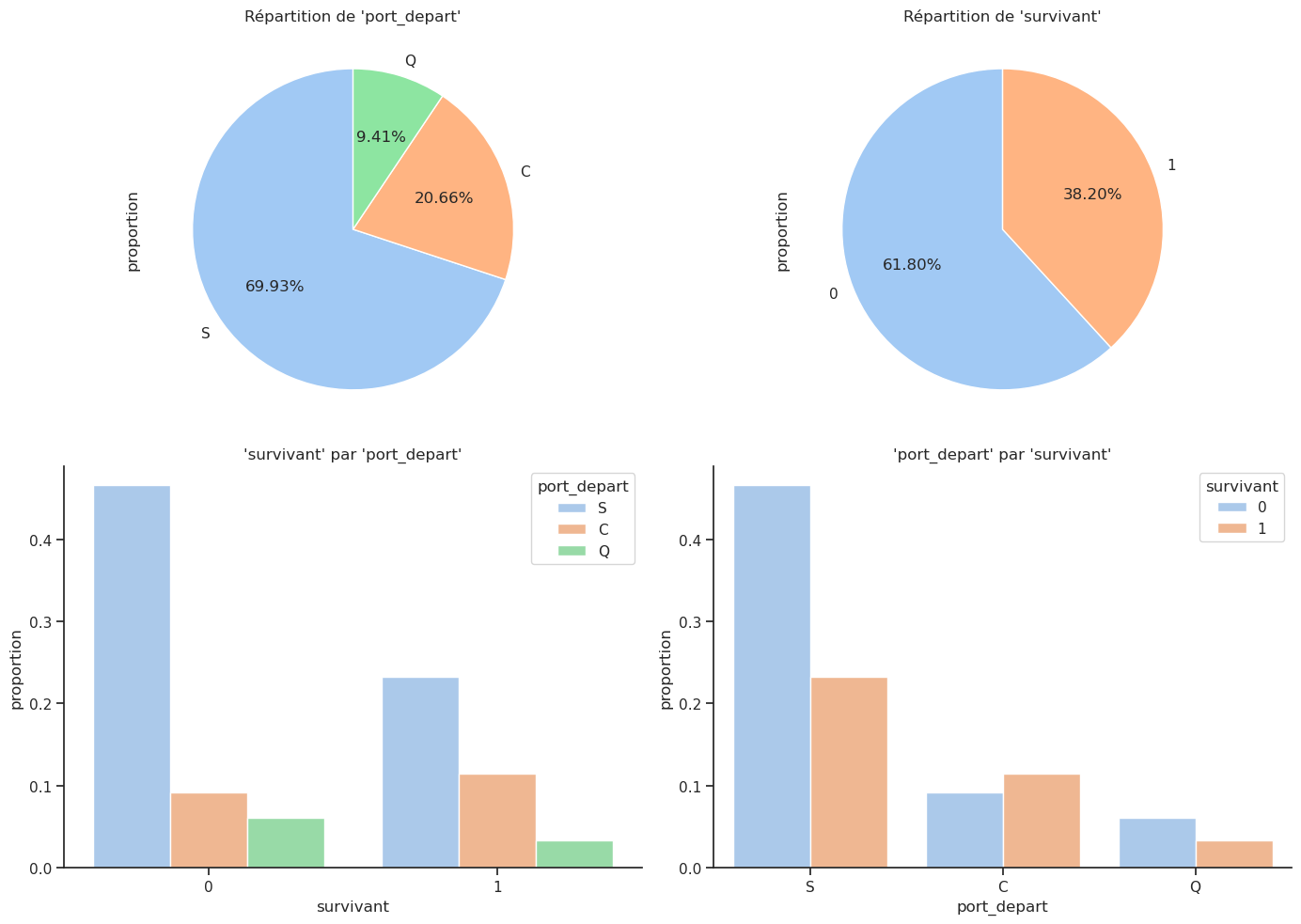
plot_proportions(df, 'port_depart', 'survivant')

Crosstab absolu :

survivant	0	1	Total
port_depart
C	120	150	270
Q	79	44	123
S	610	304	914
Total	809	498	1307

Crosstab normalisé par ligne :

survivant	0	1
port_depart
C	0.444444	0.555556
Q	0.642276	0.357724
S	0.667396	0.332604
Total	0.618975	0.381025

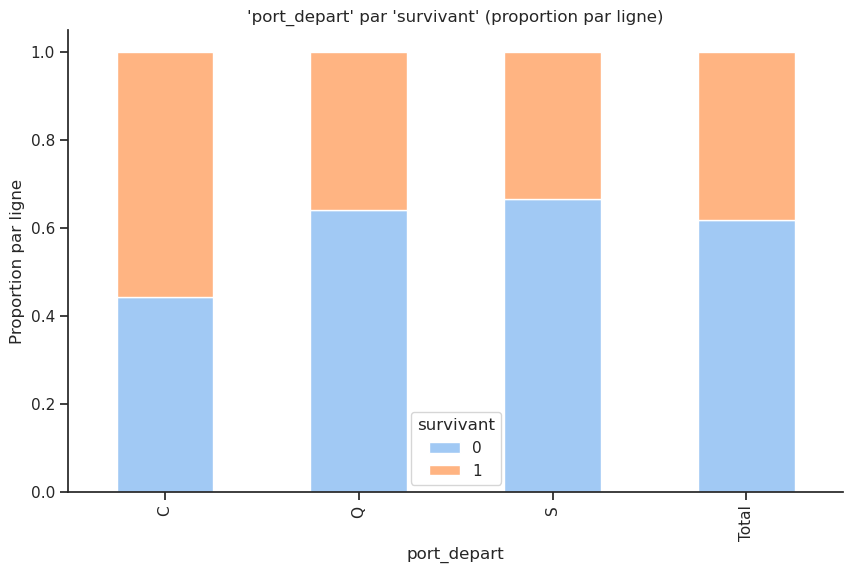
D’après ces graphiques, environ 70 % des passagers ont embarqué depuis S(outhampton), 20 % depuis C(herbourg) et 10 % depuis Q(ueenstown). Cependant, le taux de survie le plus élevé, soit 55 %, est obtenu pour les passagers ayant embarqué à Cherbourg, puis environ 35 % à Queenstown et 30 % à Southampton.

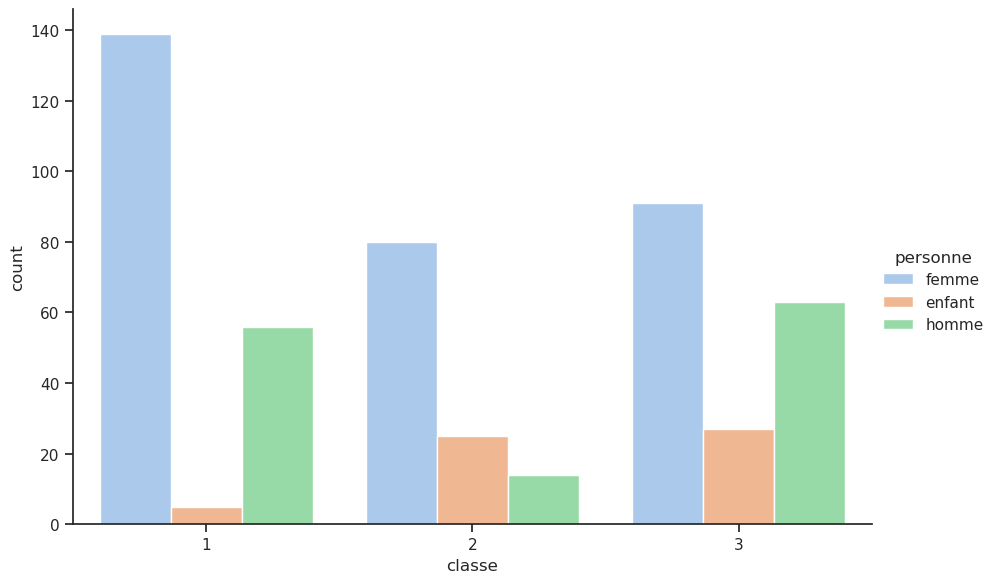
4.7 Bonus : nouvelle colonne femmes / hommes / enfants

Il pourrait être utile de connaître la répartition entre les hommes, les femmes et les enfants. Pour cela, nous allons créer une nouvelle colonne personne qui prendra les valeurs homme, femme ou enfant en fonction de l’âge. Nous allons ensuite afficher le taux de survie pour chaque catégorie de personnes.

Cependant, la priorité pour l’évacuation selon le fameux principe « les femmes et les enfants d’abord » ne définissait pas exactement un âge officiel pour les enfants. Les archives et témoignages historiques montrent que les enfants étaient généralement considérés comme ceux de moins de 14 ans. Certains témoignages mentionnent que des adolescents (12-15 ans) étaient parfois traités comme des adultes selon le contexte et la cabine. Les décisions étaient aussi un peu arbitraires : la distinction reposait souvent sur l’apparence et la taille plutôt que sur un âge strict. Donc, pour les analyses de survie ou des modèles statistiques sur le Titanic, beaucoup de chercheurs prennent <15 ans comme enfant pour appliquer ce critère.

df['personne'] = df['sexe']
df['personne'] = df['personne'].replace({'H':'homme', 'F':'femme'})
df.loc[df['age']<14, 'personne'] = 'enfant'

sns.catplot(x='classe', data=df, hue='personne', kind='count');

# sns.catplot(x='classe', y='survivant', data=df, hue='personne', kind='point')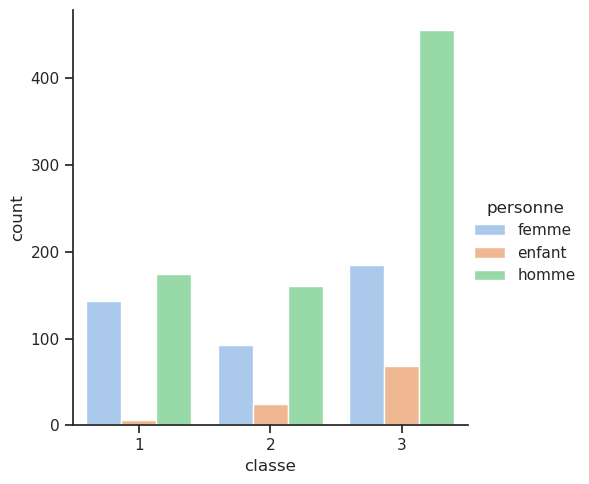

px.histogram(df, x='classe', color='personne', text_auto=True).update_layout(bargap=0.2).show()

Unable to display output for mime type(s): application/vnd.plotly.v1+json

# Graphique pour le nombre absolu de survivants
sns.catplot(
    x='classe', 
    hue='personne', 
    data=df[df['survivant'] == 1], 
    kind='count', 
    height=6, 
    aspect=1.5
);

df_survivants = df[df['survivant'] == 1]
px.histogram(df_survivants, x='classe', color='personne', text_auto=True).update_layout(bargap=0.2).show()

Unable to display output for mime type(s): application/vnd.plotly.v1+json

4.8 Classe / Âge / Survie

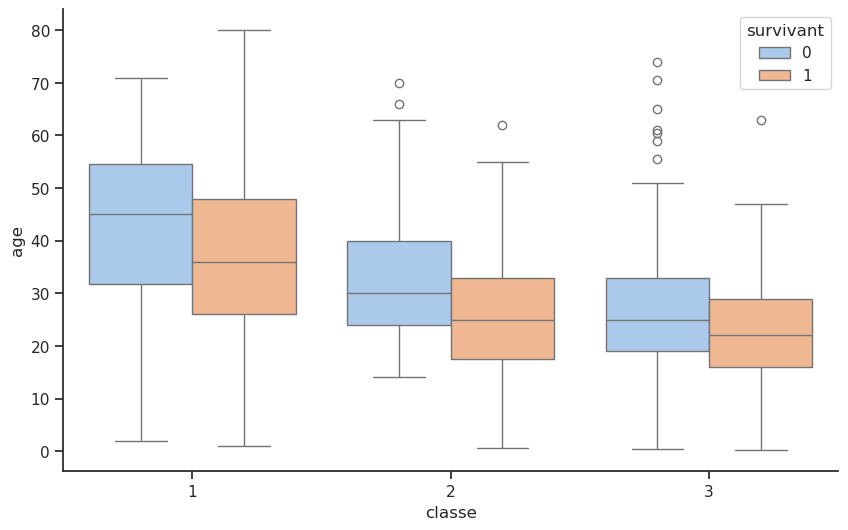
Quelle est la distribution de l’âge des passagers en fonction de la classe ?

# df.groupby('classe')['age'].mean()
df.pivot_table(values='age', index='classe', aggfunc='mean')

	age
classe
1	39.159918
2	29.506705
3	24.816367

# plot_proportions(df, 'age_group', 'classe')

Nous souhaitons analyser comment une variable continue (comme l’âge) varie au sein de groupes catégoriels (comme la classe), tout en distinguant les sous-groupes à l’intérieur de chaque catégorie à l’aide d’une variable de différenciation (ici, le statut de survivant). Ce type de graphique permet d’avoir une vue claire des distributions, de voir si certaines catégories ont des valeurs extrêmes ou des tendances particulières, et de faire des comparaisons entre des groupes sous différents critères.

sns.boxplot(data=df, x='classe', y='age', hue='survivant');

sns.FacetGrid(df, 
              col='classe', 
              hue='survivant', 
              sharex=True, 
              sharey=False, 
              ).map(sns.kdeplot, 'age', fill=True, alpha=0.15).add_legend();
plt.tight_layout()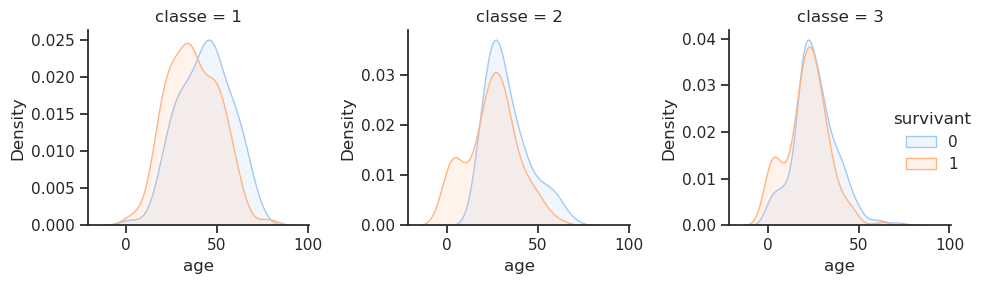

Avantage de la première classe à tous les âges : pour les passagers de première classe, la courbe de densité de survie (orange) reste systématiquement supérieure à la courbe des non-survivants (bleue) dans presque toutes les tranches d’âge. Cela indique que le statut de première classe conférait un fort avantage en termes de survie, quel que soit l’âge.
Dans les classes moyenne et inférieure, la courbe de survie atteint un pic marqué chez les plus jeunes (0-10 ans), confirmant que la politique « les femmes et les enfants d’abord » offrait un avantage en termes de survie aux enfants, même dans les classes inférieures.
Les graphiques mettent en évidence comment la combinaison de l’âge et de la classe sociale a déterminé les chances de survie : un jeune enfant, quelle que soit sa classe sociale, avait plus de chances de survivre qu’un jeune adulte de la même classe sociale. Un jeune adulte de troisième classe avait beaucoup moins de chances de survivre qu’un jeune adulte de première classe, comme le montre clairement le pic bleu proéminent pour Pclass=3 chez les 20-30 ans.

# cat pour categorical, comme la variable 'classe'
sns.catplot(data=df, x='classe', y='age', hue='survivant', alpha=0.5);

px.strip(df, x='classe', y='age', color='survivant')

Unable to display output for mime type(s): application/vnd.plotly.v1+json

4.9 Sexe / Âge / Survie

sns.FacetGrid(df, 
              col='sexe', 
              hue='survivant', 
              sharex=True, 
              sharey=False, 
              ).map(sns.kdeplot, 'age', fill=True, alpha=0.15).add_legend();
plt.tight_layout()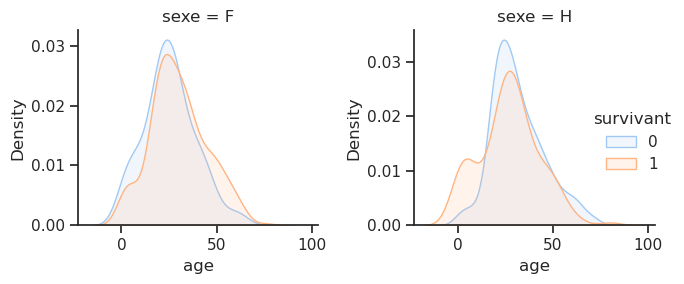

Le graphique de survie des passagers masculins révèle un désavantage prononcé. La courbe des non-survivants (en bleu) reste systématiquement plus élevée que celle des survivants (en orange) pour presque tous les âges, du jeune âge adulte à la vieillesse. La seule exception est un petit pic dans la courbe de survie autour de 0 à 5 ans, qui représente les jeunes garçons ayant bénéficié de la politique « les femmes et les enfants d’abord ». Le pic le plus marqué de la courbe des hommes non survivants se situe au début de la vingtaine, ce qui souligne que les jeunes hommes constituaient le groupe le plus vulnérable. Ils étaient les derniers à avoir accès aux canots de sauvetage et devaient faire face à des difficultés physiques importantes pour s’échapper des cabines situées sur les ponts inférieurs.

En revanche, le graphique de survie des passagères montre que la courbe des survivantes (en orange) est supérieure à celle des non-survivantes (en bleu) pour la majorité des tranches d’âge. Les chances de survie des femmes étant nettement supérieures à celles des hommes.

# cat pour categorical, comme la variable 'sexe'
sns.catplot(data=df, x='sexe', y='age', hue='survivant', marker="*", alpha=0.5);

px.strip(df, x='sexe', y='age', color='survivant')

Unable to display output for mime type(s): application/vnd.plotly.v1+json

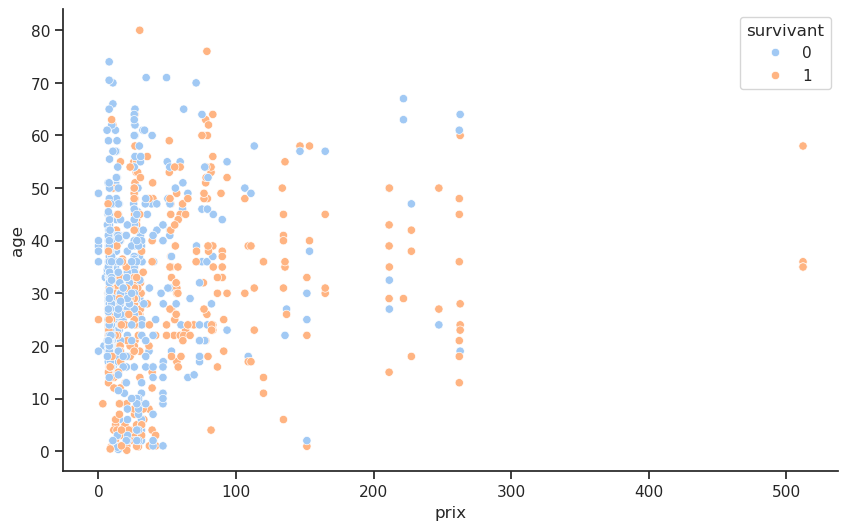
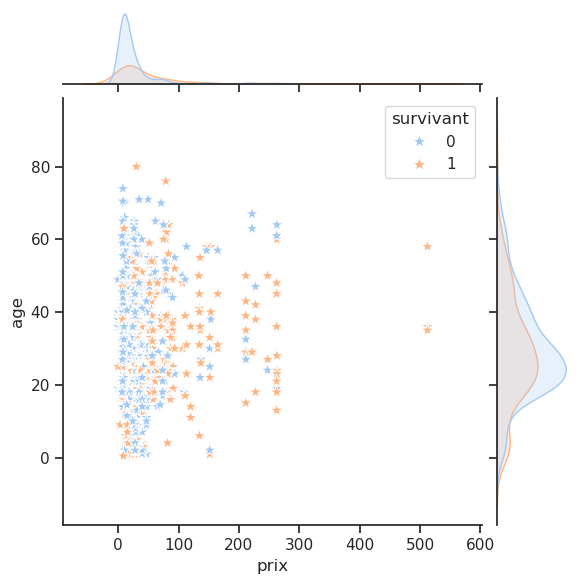
4.10 Prix / Âge / Survie

sns.scatterplot(data=df, x='prix', y='age', hue='survivant');

px.scatter(df, x='prix', y='age', color='survivant', opacity=0.5)

Unable to display output for mime type(s): application/vnd.plotly.v1+json

La fonction jointplot ajoute des informations sur leurs distributions respectives sur les bords du graphique (grâce à des histogrammes ou des KDEs).

# joint
sns.jointplot(data=df, x='prix', y='age', hue='survivant', marker="*", s=100);

px.scatter(df, x='prix', y='age', color='survivant', marginal_x='histogram', marginal_y='histogram')

Unable to display output for mime type(s): application/vnd.plotly.v1+json

4.11 Classe / Sexe / Survie

Regroupons les données d’abord par sexe et classe, puis sélectionnons le taux de survie et enfin calculons le taux de survie moyen pour chaque groupe.

df.groupby(['sexe','classe'])['survivant'].agg('mean').unstack()

classe	1	2	3
sexe
F	0.965278	0.886792	0.490741
H	0.340782	0.146199	0.152130

On note que la classe sociale a un impact sur la survie. Les femmes de première classe ont survécu à 96 %, contre 50 % pour celle de troisième classe. En ce qui concerne les hommes, 36 % des hommes de première classe ont survécu, contre 13 % pour ceux de troisième classe.

sns.barplot(data=df, x='classe', y='survivant', hue='sexe', 
            errorbar=None, palette={'F': 'pink', 'H': 'blue'});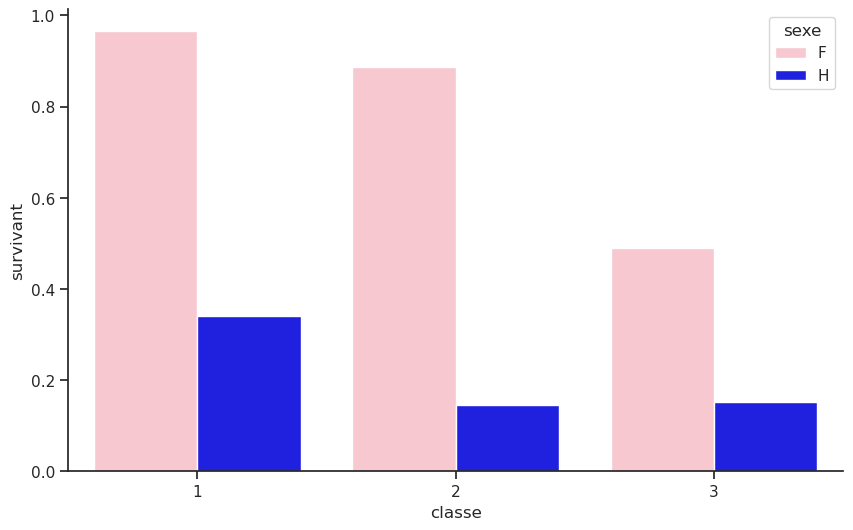

Pour obtenir les mêmes résultats que précédemment, on peut utiliser la méthode pivot_table() qui permet de créer un tableau croisé dynamique. Voici un petit dessin pour comprendre :

Combien de survivants par classe et sexe ?

df.pivot_table(index='sexe', columns='classe', values='survivant', aggfunc='sum')

classe	1	2	3
sexe
F	139	94	106
H	61	25	75

df.pivot_table(index='sexe', columns='classe', values='survivant', aggfunc='mean')

classe	1	2	3
sexe
F	0.965278	0.886792	0.490741
H	0.340782	0.146199	0.152130

La même information peut être affichée sous forme de mappe de chaleur (heatmap) :

pivot = df.pivot_table(values="survivant", index="sexe", columns="classe", aggfunc="mean")
sns.heatmap(pivot, annot=True, cmap="Blues", fmt=".2f")
plt.title("Survival Rate by Sex & Class")
plt.show()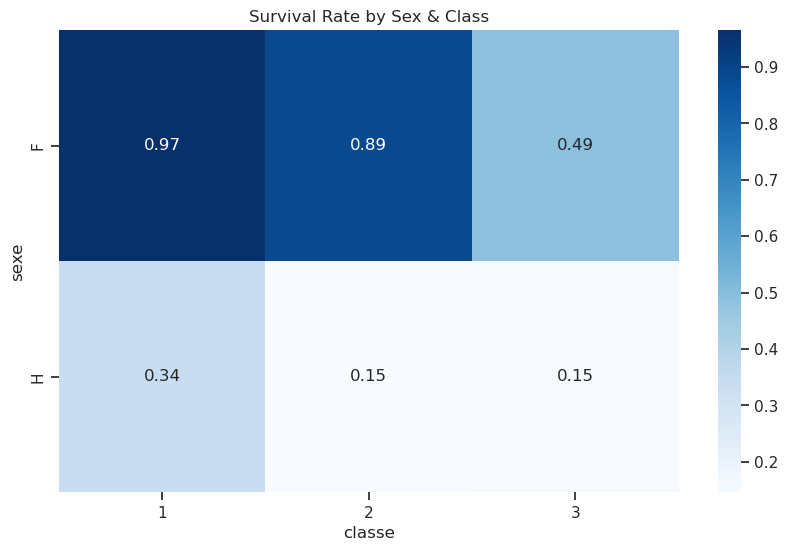

On peut spécifier plusieurs niveaux d’index pour obtenir des résultats plus détaillés, ici on a ajouté le groupe d’âge et, pour chaque groupe, le sexe.

df.pivot_table(index=['age_group','sexe'], columns='classe', values='survivant', aggfunc='sum', observed=False)

	classe	1	2	3
age_group	sexe
0-10	F	0.0	11.0	14.0
0-10	H	3.0	11.0	11.0
10-20	F	15.0	15.0	20.0
10-20	H	3.0	2.0	9.0
20-30	F	32.0	34.0	25.0
20-30	H	12.0	5.0	26.0
30-40	F	33.0	19.0	9.0
30-40	H	14.0	3.0	11.0
40-50	F	22.0	11.0	3.0
40-50	H	13.0	1.0	2.0
50-60	F	21.0	2.0	NaN
50-60	H	7.0	0.0	0.0
60-70	F	4.0	NaN	1.0
60-70	H	0.0	1.0	0.0
70-80	F	1.0	NaN	NaN
70-80	H	1.0	NaN	0.0
Unknown	F	11.0	2.0	34.0
Unknown	H	8.0	2.0	16.0

La même technique peut s’appliquer pour les colonnes :

df.pivot_table(index=['age_group','sexe'], columns=['classe','port_depart'], values='survivant', aggfunc='sum', observed=False)

	classe	1			2			3
	port_depart	C	Q	S	C	Q	S	C	Q	S
age_group	sexe
0-10	F	NaN	NaN	0.0	2.0	NaN	9.0	6.0	NaN	8.0
0-10	H	1.0	NaN	2.0	1.0	NaN	10.0	2.0	0.0	9.0
10-20	F	5.0	NaN	10.0	2.0	NaN	13.0	7.0	4.0	9.0
10-20	H	2.0	NaN	1.0	1.0	NaN	1.0	3.0	0.0	6.0
20-30	F	16.0	NaN	16.0	7.0	1.0	26.0	2.0	4.0	19.0
20-30	H	7.0	NaN	5.0	2.0	NaN	3.0	5.0	2.0	19.0
30-40	F	15.0	2.0	15.0	NaN	NaN	19.0	1.0	0.0	8.0
30-40	H	6.0	NaN	8.0	0.0	0.0	3.0	1.0	0.0	10.0
40-50	F	15.0	NaN	7.0	NaN	NaN	11.0	1.0	NaN	2.0
40-50	H	6.0	0.0	7.0	0.0	NaN	1.0	0.0	0.0	2.0
50-60	F	11.0	NaN	10.0	NaN	NaN	2.0	NaN	NaN	NaN
50-60	H	4.0	NaN	3.0	NaN	0.0	0.0	NaN	NaN	0.0
60-70	F	1.0	NaN	2.0	NaN	NaN	NaN	NaN	NaN	1.0
60-70	H	0.0	NaN	0.0	NaN	0.0	1.0	NaN	0.0	0.0
70-80	F	NaN	NaN	1.0	NaN	NaN	NaN	NaN	NaN	NaN
70-80	H	0.0	NaN	1.0	NaN	NaN	NaN	NaN	0.0	0.0
Unknown	F	6.0	NaN	5.0	NaN	1.0	1.0	5.0	25.0	4.0
Unknown	H	2.0	NaN	6.0	1.0	0.0	1.0	4.0	5.0	7.0

Pourcentage de survivants par sexe et age :

df.pivot_table(index='sexe', columns='age_group', values='survivant', aggfunc='sum', observed=False) 
# Comme la colonne 'survivant' vaut 0 si décédé et 1 si survivant, la somme donne le nombre de survivants

age_group	0-10	10-20	20-30	30-40	40-50	50-60	60-70	70-80	Unknown
sexe
F	25	50	91	61	36	23	5	1	47
H	25	14	43	28	16	7	1	1	26

4.12 Classe / Prix / Survie

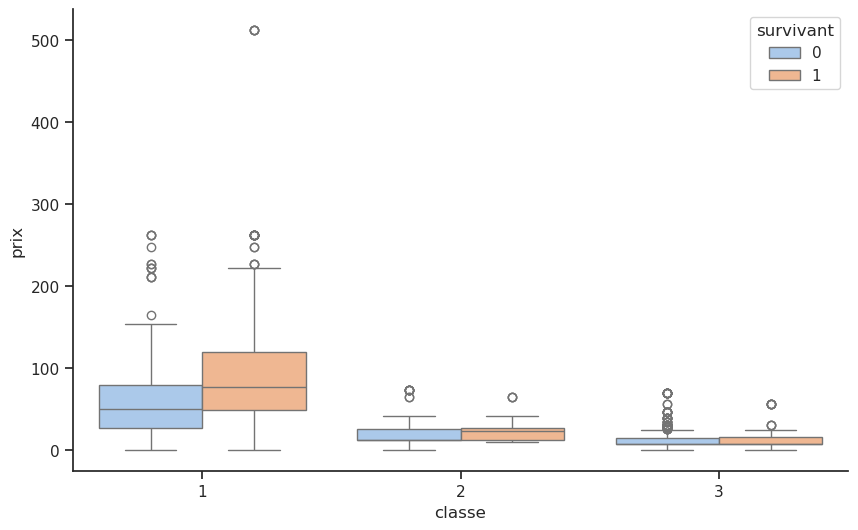
sns.boxplot(data=df, x='classe', y='prix', hue='survivant');

Le diagramme en boîte « Répartition des tarifs par classe et survie » offre une perspective plus détaillée sur la manière dont la richesse, telle que reflétée par le prix du billet, a influencé les chances de survie.

Première classe (classe = 1) : parmi les passagers de première classe, les survivants (boîte orange) avaient un tarif médian nettement plus élevé que les non-survivants (boîte bleue). Cela suggère que même au sein de ce groupe privilégié, les passagers ayant payé plus cher ont bénéficié de meilleures chances de survie, probablement grâce à des cabines situées plus près des ponts supérieurs et des canots de sauvetage. Les valeurs extrêmes à l’extrémité supérieure du graphique des tarifs des survivants indiquent que les passagers les plus riches, qui ont payé des tarifs exceptionnellement élevés, ont presque tous survécu.

Deuxième classe (classe = 2) : la différence entre les tarifs médians des survivants et des non-survivants est moins frappante, mais toujours présente. Les survivants ont tendance à avoir des tarifs légèrement plus élevés, ce qui suggère un léger avantage lié au fait de payer plus cher, bien que cet effet soit moins marqué qu’en première classe.

Troisième classe (classe = 3) : pour les passagers de troisième classe, la répartition des tarifs est uniformément basse, avec presque aucune différence entre les survivants et les non-survivants. Dans ce groupe, le prix du billet a eu un impact minime sur la survie. Les obstacles physiques importants que représentaient les ponts inférieurs et l’accès limité aux canots de sauvetage ont éclipsé les différences économiques mineures.


sns.kdeplot(df[df['survivant']==0]['prix'], fill=True, alpha=0.25, label='Décédés', color='red')
sns.kdeplot(df[df['survivant']==1]['prix'], fill=True, alpha=0.25, label='Survivants', color='green')
plt.legend();

4.13 Prix / Âge / Sexe / Survie

Nous souhaitons explorer la relation entre le prix payé et l’âge, tout en tenant compte du statut de survie (survivant) et du sexe.

La commande lmplot() est utilisée pour afficher une régression linéaire entre deux variables continues tout en permettant de visualiser la relation à l’aide de couleurs et de facettes.

Le graphique affiche une régression linéaire entre les deux variables continues prix et age. Cela signifie qu’une droite (ou un autre modèle de régression si spécifié) est tracée pour chaque groupe de la variable survivant. La ligne de régression montre la tendance générale de la relation entre prix et âge. Par exemple, on observe que les personnes plus âgées ont tendance à payer plus cher.
En fonction de la variable hue='survivant', chaque groupe (survivant vs non-survivant) aura une couleur différente. Cela permet de comparer les relations entre prix et âge pour chaque groupe de manière visuellement distincte.
Grâce à l’argument col='sexe', on a des graphiques séparés pour chaque niveau de la variable sexe. Cela permet de visualiser comment la relation entre prix et âge varie entre les hommes et les femmes, par exemple.
Le paramètre markers=['o', 'x'] permet d’utiliser différents types de marqueurs pour les points représentant les survivants et les non-survivants, facilitant ainsi la distinction visuelle entre les deux groupes.

Ce graphique est pertinent si on pense que la relation entre deux variables continues est linéaire (ou presque linéaire) et souhaitons l’examiner graphiquement tout en incluant des groupes distincts (par exemple, selon survivant).

# On ajoute une quatrième dimension : le sexe
sns.lmplot(data=df, x='prix', y='age', hue='survivant', col='sexe', markers=['o', 'x'], palette='Set1');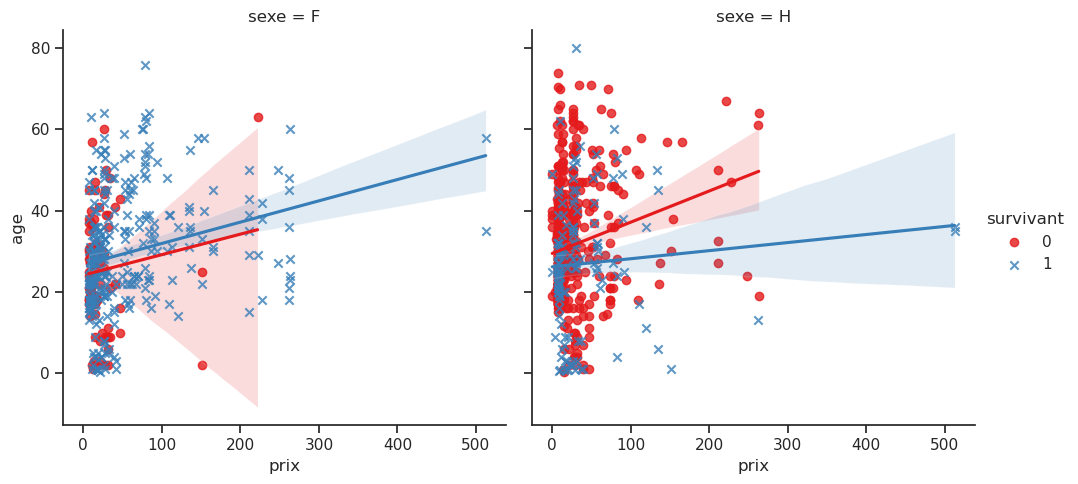

Un graphique 3D avec la couleur comme 4e dimension est également possible :

# df['survivant'] = df['survivant'].astype('category')

df['survivant_code'] = df['survivant'].map({0: 'Non', 1: 'Oui'})

px.scatter_3d(
    df, 
    x='prix', 
    y='age', 
    z='sexe', 
    # color='survivant',
    color='survivant_code', 
    # Si la colonne est numérique, on peut la colorer mais il faut color_continuous_scale
    # color_continuous_scale='sunset',
    # On l'a transformée en catégorielle pour utiliser color_discrete_sequence
    color_discrete_sequence=['green', 'red'],  # il faut que 'survivant' soit une variable catégorielle !
    # labels={'prix': 'Prix', 'age': 'Âge', 'sexe': 'Sexe', 'survivant_code': 'Survivant'},
    # title='Classe vs Age vs Sexe selon le statut de survie',
)

Unable to display output for mime type(s): application/vnd.plotly.v1+json

5 Miscellanea

5.1 `groupby()`

Cout moyen (en livres d’époque) des billets par classe.

Selon (Wikipedia)[https://fr.wikipedia.org/wiki/Passagers_du_Titanic#Le_naufrage_et_son_bilan], le prix moyen des billets était de 7 livres de l’époque pour la troisième classe. Notre jeu de données indique un prix moyen de 13,30 livres pour la troisième classe, ce qui semble un peu élevé. Cependant, il est possible que notre jeu de données ne contienne pas tous les passagers de troisième classe.

df.groupby('classe')['prix'].mean().to_frame()

	prix
classe
1	87.508992
2	21.179196
3	13.302889

5.2 Filtres et `value_counts`

Parmi les enfants, les filles ont-elles été plus sauvées que les garçons ?

mask_mineur_homme = (df['age'] < 10) & (df['sexe']=="H")
df[mask_mineur_homme]['survivant'].value_counts()

survivant
1    25
0    18
Name: count, dtype: int64

mask_mineur_femme = (df['age'] < 10) & (df['sexe']=="F")
df[mask_mineur_femme]['survivant'].value_counts()

survivant
1    25
0    14
Name: count, dtype: int64

5.3 Corrélation entre les données : `corr`

La corrélation est le degré auquel deux ou plusieurs attributs ou mesures sur le même groupe d’éléments ont tendance à varier ensemble.

Les corrélations sont parmi les éléments les plus courants et les plus utiles de l’analyse des données. Qu’est-ce qui bouge avec quoi ? Quelles variables sont « dépendantes » et lesquelles sont « indépendantes » ? Quelles sont donc les questions pour lesquelles nous pourrions vouloir trouver des corrélations ?

Quelles sont les corrélations que nous pourrions rechercher ?

Existe-t-il une corrélation entre l’âge et le prix du billet ?
Existe-t-il une corrélation entre la classe et la survie ? Les riches ont-ils survécu davantage que les travailleurs ?
Y a-t-il une corrélation entre l’âge et la survie ?
Les femmes et les enfants ont-ils vraiment le droit de passer en premier ?

Nous connaissons tous le vieil adage selon lequel, lorsqu’un navire coule, ce sont « les femmes et les enfants d’abord » qui montent à bord des canots de sauvetage. Ce vieil adage s’est-il vérifié sur le Titanic ? Les femmes et les enfants ont-ils été plus nombreux à survivre que les hommes ? Le sexe, l’âge ou la classe sociale des passagers du Titanic ont-ils joué un rôle déterminant dans leur survie ?

Si les femmes et les enfants ont survécu plus que les hommes, il devrait y avoir une corrélation positive entre la survie et le sexe et la survie et l’âge.

La méthode .corr() de pandas permet de trouver la corrélation entre deux caractéristiques quelconques d’un jeu de données.

df['age'].corr(df['survivant'])

-0.055512520192146246

Une valeur +1 signifie qu’il existe une corrélation positive parfaite entre deux caractéristiques, c’est-à-dire que lorsqu’une caractéristique augmente, l’autre augmente exactement dans les mêmes proportions.

Zéro signifie qu’il n’y a pas de corrélation entre deux caractéristiques. Elles se déplacent complètement au hasard l’une par rapport à l’autre.

Une valeur -1 signifie qu’il existe une corrélation parfaite, négative ou inverse entre deux caractéristiques. Lorsqu’une caractéristique augmente, l’autre diminue et vice versa.

D’après la corrélation entre le sexe et la survie (53 %) et l’âge et la survie (-0,05 %), nous pouvons affirmer certaines choses :

le fait qu’un passager soit un homme était fortement corrélé négativement avec sa survie à bord du Titanic.
le fait qu’un passager soit plus âgé est très faiblement corrélé négativement avec sa survie.

Mais « l’âge » n’est pas « les enfants », n’est-ce pas ? Comment savoir si le fait d’avoir moins de 10 ans augmentait les chances de survie ? Quelle était la probabilité qu’une personne de moins de 10 ans survive par rapport à une personne de plus de 10 ans ?

masque = df['age'] < 10
df[masque]['age'].corr(df['survivant'])

-0.14006219496281994

On ne peut pas calculer la corrélation avec le sexe car c’est une variable catégorielle. On peut utiliser la méthode groupby() pour regrouper les données par sexe et calculer la moyenne de survie pour chaque groupe. Ou sinon ajouter une colonne où les valeurs catégorielles sont encodées par des valeurs numériques, par exemple 0 pour les hommes et 1 pour les femmes.

# Catégorisation de la variable 'sexe' en 'sexe_code'
df['sexe_code'] = df['sexe'].astype('category').cat.codes
# df['sexe_code'] = df['sexe'].map({'H': 0, 'F': 1})
# df['sexe_code'] = df['sexe'].replace({'H': 0, 'F': 1})
df

	classe	survivant	sexe	age	prix	port_depart	age_group	sexe_num	port_depart_num	personne	survivant_code	sexe_code
0	1	1	F	29.0000	211.3375	S	20-30	0	2	femme	Oui	0
1	1	1	H	0.9167	151.5500	S	0-10	1	2	enfant	Oui	1
2	1	0	F	2.0000	151.5500	S	0-10	0	2	enfant	Non	0
3	1	0	H	30.0000	151.5500	S	20-30	1	2	homme	Non	1
4	1	0	F	25.0000	151.5500	S	20-30	0	2	femme	Non	0
...	...	...	...	...	...	...	...	...	...	...	...	...
1304	3	0	F	14.5000	14.4542	C	10-20	0	0	femme	Non	0
1305	3	0	F	NaN	14.4542	C	Unknown	0	0	femme	Non	0
1306	3	0	H	26.5000	7.2250	C	20-30	1	0	homme	Non	1
1307	3	0	H	27.0000	7.2250	C	20-30	1	0	homme	Non	1
1308	3	0	H	29.0000	7.8750	S	20-30	1	2	homme	Non	1

1309 rows × 12 columns

Pour l’instant, examinons la matrice de corrélation.

corr_matrix = df[['survivant', 'sexe_code', 'age', 'classe', 'prix']].corr()

# Ordonner les colonnes et les lignes selon la corrélation avec la variable 'survivant'
sorted_columns = corr_matrix['survivant'].abs().sort_values(ascending=False).index
sorted_corr_matrix = corr_matrix.loc[sorted_columns, sorted_columns]

corr_matrix['survivant']

survivant    1.000000
sexe_code   -0.528693
age         -0.055513
classe      -0.312469
prix         0.244265
Name: survivant, dtype: float64

# Avec Seaborn
# ---------------------------
# sns.heatmap(sorted_corr_matrix, linewidths=0.5, annot=True, cbar=True, cmap="coolwarm")
# plt.show()

#Avec plotly.express
# ---------------------------
px.imshow(sorted_corr_matrix, 
          text_auto='.2f', 
          color_continuous_scale='RdBu_r', 
          aspect='auto').show()

Unable to display output for mime type(s): application/vnd.plotly.v1+json

# df['personne_code'] = df['personne'].astype('category').cat.codes
# corr_matrix = df[['survivant','personne_code','age','classe']].corr()
# sorted_columns = corr_matrix['survivant'].abs().sort_values(ascending=False).index
# sorted_corr_matrix = corr_matrix.loc[sorted_columns, sorted_columns]
# plt.figure(figsize=(10, 10))
# sns.heatmap(sorted_corr_matrix, linewidths=0.5, annot=True, cbar=True, cmap="coolwarm");

# dftemp = df[['survivant','sexe_code','age','classe']]
# corr_matrix = dftemp.corr()['survivant'].sort_values(ascending=False)

# # Sélection des colonnes ordonnées par corrélation avec 'survivant' (à l'exclusion de 'survivant' elle-même)
# sorted_columns = corr_matrix.index.tolist()[1:]

# # Création du heatmap avec Seaborn
# sns.heatmap(dftemp[sorted_columns].corr(), annot=True, linewidths=0.5, cmap="coolwarm", cbar=True);

6 Autres ressources

Voici trois excellentes vidéos (en français) de la chaîne YouTube Machine Learnia qui expliquent comment faire une analyse statistique du jeu de données du Titanic :

Vidéo 1 : Analyse exploratoire de données

Vidéo 2 : Data visualization (à partir de 19:50)

Vidéo 3 : Feature engineering (à partir de 6:35)

7 Pour aller plus loin : 🧹 analyse exploratoire 🧹 → 🔮 prédiction 🔮

Dans cette exploraiton du dataset Titanic avec Pandas, nous avons vu comment filtrer et sélectionner des données, faire des statistiques descriptives, croiser et agréger des variables, visualiser les résultats avec différents types de graphiques. Tout cela nous permet de comprendre les facteurs qui influencent la survie des passagers. Mais ces outils restent des analyses descriptives : ils montrent des relations, mais ne permettent pas de prédire directement le destin d’un passager inconnu.

Une fois que l’on a identifié les facteurs importants, on peut se poser la question : “Peut-on prédire si un passager va survivre ou non à partir de ses caractéristiques (âge, sexe, classe, tarif, etc.) ?”

La prédiction cherche à estimer une valeur future ou inconnue sur la base de données existantes. Les étapes générales pour prédire sont les suivantes :

Préparer et explorer les données.
Choisir un modèle : régression logistique, arbres de décision, réseaux de neurones, etc.
Séparer les données en train set (pour entraîner le modèle) et test set (pour évaluer la performance)
Entraîner le modèle sur les données existantes (train set)
Évaluer le modèle sur des données jamais vues (test set) et évaluer la performance avec des métriques adaptées (accuracy, precision, recall)

Pandas est utilisé pour la préparation des données avant de les passer à un modèle de machine learning.

Dans le cas du Titanic :

Variable cible : survivant (0 = mort, 1 = survécu)
Features (variables explicatives) : classe, sexe, age, port_depart, etc.

C’est un problème de classification : prédire une catégorie (0 ou 1) à partir des autres caractéristiques.

Observations après l’analyse exploratoire :

les femmes ont survécu plus souvent que les hommes
les passagers de première classe ont survécu plus souvent que ceux de troisième classe
les enfants ont un taux de survie légèrement supérieur à celui des adultes

Un modèle de prédiction pourrait apprendre ces patterns et estimer la probabilité de survie d’un passager inconnu.

Conclusion
L’analyse exploratoire avec Pandas est la première étape pour comprendre les données et identifier les facteurs influençant la survie des passagers. Pour aller plus loin, on peut passer à la prédiction : estimer si un passager inconnu survivra ou non à partir de ses caractéristiques.

Cette étape implique le machine learning, où l’on choisit un modèle (régression logistique, arbres de décision, réseau de neurones…), on entraîne ce modèle sur un train set, puis on évalue sa performance sur un test set jamais vu.

Les modèles de machine learning permettent non seulement de quantifier l’impact de chaque variable, mais aussi de capturer des relations complexes entre elles. Les réseaux de neurones (deep learning) sont particulièrement utiles lorsque les patterns sont non linéaires ou que les datasets sont volumineux.

Ainsi, le workflow complet va de l’observation des données à la prise de décision prédictive, illustrant comment l’intelligence artificielle appliquée aux données réelles peut aider à estimer des probabilités et guider des actions.

Voici plusieurs modèles de prédiction avec la bibliothèque Scikit-Learn pour les entraîner sur le dataset Titanic :

from sklearn.model_selection import train_test_split

from sklearn.dummy import DummyClassifier
from sklearn.linear_model import LogisticRegression
from sklearn.neural_network import MLPClassifier
from sklearn.neighbors import KNeighborsClassifier
from sklearn.ensemble import RandomForestClassifier, GradientBoostingClassifier
from sklearn.tree import DecisionTreeClassifier
from sklearn.svm import SVC
from sklearn.naive_bayes import GaussianNB
from sklearn.linear_model import SGDClassifier
# from sklearn.cluster import KMeans
# from sklearn.decomposition import PCA

from sklearn.metrics import accuracy_score, confusion_matrix, precision_score, recall_score, f1_score
from sklearn.preprocessing import StandardScaler

# ---------------------------------------------------------
# 1. PRÉPARATION DES DONNÉES (COMMUNE AUX MODÈLES)
# ---------------------------------------------------------

data = df.copy()

# Remplacer les valeurs manquantes
data['age'].fillna(data['age'].median(), inplace=True)

# Encoder les variables catégorielles
data['sexe_num'] = data['sexe'].astype('category').cat.codes
    
# Features et cible
X = data[['classe', 'sexe_num', 'age']]
y = data['survivant']

# Train/Test
X_train, X_test, y_train, y_test = train_test_split(
    X, y, test_size=0.2, random_state=42, 
    stratify=y # pour conserver la même proportion de survivants dans train et test
)
display(Markdown(f"Dimension de X_train : {X_train.shape}, Dimension de X_test : {X_test.shape}"))

# Normalisation (utile pour MLP, k-NN, SVC)
scaler = StandardScaler()
X_train_scaled = scaler.fit_transform(X_train)
X_test_scaled = scaler.transform(X_test)



# ---------------------------------------------------------
# 2. LISTE DES MODÈLES
# ---------------------------------------------------------

models = [
    ("Baseline (Dummy)", DummyClassifier(strategy='most_frequent', random_state=42)),
    ("Régression logistique", LogisticRegression(max_iter=1000)),
    ("Réseau de neurones (MLP)", MLPClassifier(hidden_layer_sizes=(32,16),
                                               activation='logistic', # 'relu', 'tanh'
                                               solver='adam',
                                               learning_rate='adaptive',
                                               learning_rate_init=0.01,
                                               early_stopping=True,
                                               n_iter_no_change=20,
                                               max_iter=500,
                                               random_state=42)),
    ("k-Nearest Neighbors", KNeighborsClassifier(n_neighbors=5)),
    ("Random Forest", RandomForestClassifier(criterion='gini', n_estimators=450, random_state=1, max_depth=20, min_samples_leaf=3, min_samples_split=2) ),
    ("Decision Tree", DecisionTreeClassifier(random_state=42)),
    ("Stochastic Gradient Descent", SGDClassifier(max_iter=1000, tol=1e-3, random_state=42)),   
    ("Gradient Boosting", GradientBoostingClassifier(n_estimators=100, random_state=42)),
    ("Support Vector Classifier", SVC(kernel='rbf', probability=True, random_state=42)),
    ("Naive Bayes (Gaussian)", GaussianNB())
]

# ---------------------------------------------------------
# 3. ENTRAÎNEMENT ET STOCKAGE DES RÉSULTATS
# ---------------------------------------------------------

results = []

for name, model in models:
    if name in ["Régression logistique", "Réseau de neurones (MLP)", "k-Nearest Neighbors", "Support Vector Classifier"]:
        model.fit(X_train_scaled, y_train)
        y_pred = model.predict(X_test_scaled)
    else:
        model.fit(X_train, y_train)
        y_pred = model.predict(X_test)
    
    acc = accuracy_score(y_test, y_pred)
    prec = precision_score(y_test, y_pred, zero_division=0)
    rec = recall_score(y_test, y_pred)
    f1 = f1_score(y_test, y_pred)
    cm = confusion_matrix(y_test, y_pred)
    
    # Extraction des valeurs pour classification binaire
    if cm.shape == (2,2):
        TN, FP, FN, TP = cm.ravel()
    else:
        TN = FP = FN = TP = None
    
    results.append({
        "Modèle": name,
        "Accuracy": acc,
        "Précision": prec,
        "Rappel": rec,
        "F1-Score": f1,
        "Vrai 0 / Prédit 0": TN,
        "Vrai 1 / Prédit 1": TP,
        "Vrai 0 / Prédit 1": FP,
        "Vrai 1 / Prédit 0": FN
    })

final_df = pd.DataFrame(results)
final_df.sort_values(by='Accuracy', ascending=False)

Dimension de X_train : (1047, 3), Dimension de X_test : (262, 3)

	Modèle	Accuracy	Précision	Rappel	F1-Score	Vrai 0 / Prédit 0	Vrai 1 / Prédit 1	Vrai 0 / Prédit 1	Vrai 1 / Prédit 0
8	Support Vector Classifier	0.835878	0.880000	0.66	0.754286	153	66	9	34
7	Gradient Boosting	0.828244	0.848101	0.67	0.748603	150	67	12	33
4	Random Forest	0.820611	0.762376	0.77	0.766169	138	77	24	23
1	Régression logistique	0.816794	0.776596	0.73	0.752577	141	73	21	27
5	Decision Tree	0.801527	0.750000	0.72	0.734694	138	72	24	28
9	Naive Bayes (Gaussian)	0.793893	0.739583	0.71	0.724490	137	71	25	29
3	k-Nearest Neighbors	0.774809	0.688073	0.75	0.717703	128	75	34	25
2	Réseau de neurones (MLP)	0.732824	0.894737	0.34	0.492754	158	34	4	66
6	Stochastic Gradient Descent	0.706107	0.810811	0.30	0.437956	155	30	7	70
0	Baseline (Dummy)	0.618321	0.000000	0.00	0.000000	162	0	0	100

7.0.1 Mesures de fiabilité des prédictions

Pour évaluer la pertinence du modèle de machine learning appliqué au Titanic, nous utilisons les métriques dérivées de la matrice de confusion.

La matrice de confusion est un tableau qui permet de visualiser les performances d’un algorithme de classification. Elle compare les prédictions du modèle avec les résultats réels :

	Prévu non-survécu	Prévu survécu
Réel non-survécu	Vrais négatifs	Faux positifs
Réel survécu	Faux négatifs	Vrais positifs

Par exemple, dans le cas du modèle SVC appliqué au dataset Titanic, la matrice de confusion est la suivante :

Vrais négatifs (VN) : le modèle a correctement prédit que 153 passagers n’ont pas survécu.
Faux positifs (FP) : le modèle a prédit que 9 passagers survivraient alors qu’ils sont morts.
Faux négatifs (FN) : le modèle a prédit que 34 passagers ne survivraient pas alors qu’ils ont survécu.
Vrais positifs (VP) : le modèle a correctement prédit que 66 passagers ont survécu.

Métriques de performance

Accuracy (précision globale)
Proportion de bonnes prédictions parmi l’ensemble des prédictions :
\[ \frac{VN+VP}{VN+VP+FP+FN} \]
Précision (precision)
Mesure la proportion de prédictions positives correctes. Elle pénalise les faux positifs.
\[ \text{precision}=\frac{VP}{VP+FP} \]
Rappel (recall ou sensibilité)
Mesure la capacité du modèle à identifier correctement les survivants (classe positive).
\[ \text{recall}=\frac{VP}{VP+FN} \]
F1-score
Moyenne harmonique entre la précision et le rappel.
\[ F_1=2\dfrac{\text{precision}\times \text{recall}}{\text{precision}+\text{recall}} \]
Spécificité
Proportion de vrais négatifs correctement identifiés.
\[ \text{spécificité}=\frac{VN}{VN+FP} \]

Interprétation des résultats

Accuracy : parmi les modèles testés, le SVC obtient la meilleure performance avec une précision globale de 83,6%. Cela signifie que 83,6% des prédictions du modèle sont correctes.
Cependant, cette mesure ne distingue pas les erreurs concernant les survivants et les non-survivants.
La matrice de confusion montre que le modèle dentifie correctement une majorité de non-survivants, sous-prédit la survie, avec 34 faux négatifs, ce qui signifie qu’un nombre significatif de survivants réels sont classés comme non-survivants.
Globalement, le modèle est performant, mais la sous-détection des survivants peut être problématique selon les objectifs de l’étude.

Retour au sommet

1 Importation des données

2 Étude globale de l’ensemble de données

2.1 Données manquantes ?

2.2 Bilan sur l’ensemble de données

2.3 Statistiques descriptives

3 Analyse univariée (chaque colonne individuellement)

3.1 Colonne nom

3.1.1 Plus jeune et plus vieux passagers

3.1.2 Plus jeune et plus vieux passagers à avoir survécu

3.1.3 Plus jeune et plus vieux passagers à être décédé

3.1.4 Le capitaine du Titanic ?

3.1.5 Curiosités

3.1.6 Doublons ?

3.1.7 Suppression de la colonne nom

3.2 Préambule: valeurs uniques dans chaque colonne

3.3 Colonne classe

3.4 Colonne sexe

3.5 Colonne survivant

3.6 Colonne age

3.7 Nouvelle Colonne age_group

4 Liens entre deux ou plusieurs colonnes

4.1 Analyse bivariée, vue d’ensemble

4.2 Classe / Survie

4.3 Sexe / Survie

4.4 Age / Survie

4.5 Age_group / Survie

4.6 Port de départ / Survie

4.7 Bonus : nouvelle colonne femmes / hommes / enfants

4.8 Classe / Âge / Survie

4.9 Sexe / Âge / Survie

4.10 Prix / Âge / Survie

4.11 Classe / Sexe / Survie

4.12 Classe / Prix / Survie

4.13 Prix / Âge / Sexe / Survie

5 Miscellanea

5.1 groupby()

5.2 Filtres et value_counts

5.3 Corrélation entre les données : corr

6 Autres ressources

7 Pour aller plus loin : 🧹 analyse exploratoire 🧹 → 🔮 prédiction 🔮

7.0.1 Mesures de fiabilité des prédictions

3.1 Colonne `nom`

3.1.7 Suppression de la colonne `nom`

3.3 Colonne `classe`

3.4 Colonne `sexe`

3.5 Colonne `survivant`

3.6 Colonne `age`

3.7 Nouvelle Colonne `age_group`

5.1 `groupby()`

5.2 Filtres et `value_counts`

5.3 Corrélation entre les données : `corr`