CM 5 - Convergence et A-stabilité des schémas 👣 multipas 👣 linéaires

Auteur·rice

Gloria FACCANONI

Date de publication

22 mars 2024

$\renewcommand{\R}{\mathbb{R}}$ $\renewcommand{\N}{\mathbb{N}}$ $\renewcommand{\dt}{\mathrm{d}t}$ $\renewcommand{\dx}{\mathrm{d}x}$ $\renewcommand{\dtau}{\mathrm{d}\tau}$ $\renewcommand{\CC}[1]{\mathscr{C}}$

Code

%reset -f

from IPython.display import display, Math, Latex, Markdown

import sympy as sp
sp.init_printing() 

import matplotlib.pyplot as plt
plt.rcParams.update({<span class="st">'font.size'</span>: <span class="dv">16</span>})
import numpy as np

Considérons le problème de Cauchy

trouver une fonction $y \colon I\subset \mathbb{R} \to \mathbb{R}$ définie sur un intervalle $I=[t_0,T]$ telle que $\begin{cases} y'(t) = \varphi(t,y(t)), &\forall t \in I=[t_0,T],\\ y(t_0) = y_0, \end{cases}$ avec $y_0$ une valeur donnée et supposons que l’on ait montré l’existence et l’unicité d’une solution $y$ pour $t\in I$.

Considérons une méthode numérique à $q=p+1$ étapes (=pas) linéaire.

Notons $\varphi_{n-j} = \varphi(t_{n-j},u_{n-j})$

Elle s’écrit sous la forme générale $ u_{n+1} = \sum_{j=0}^p a_ju_{n-j} + h\sum_{j=0}^p b_j\varphi(t_{n-j},u_{n-j}) + hb_{-1}\varphi(t_{n+1},u_{n+1}), \qquad n=p,p+1,\dots,N-1 $ où les $\{a_k\}$ et $\{b_k\}$ sont des coefficients donnés et $p\ge0$ un entier.

Remarques :

Si $b_{-1}=0$ la méthode est explicite, sinon implicite.
Les données initiales $u_0, u_1, \dots, u_p$ doivent être fournies. Mis à part $u_0$, qui est égale à $y_0$ donné, les autres valeurs, $u_1, \dots, u_p$ peuvent être obtenues à l’aide de méthodes suffisament précises.

Rappeles :

Méthodes classiques : elles sont toutes à $q=1$ pas ($p=0$): $u_{n+1} = a_0 u_n + h b_0 \varphi(t_n,u_n) + h b_{-1} \varphi(t_{n+1},u_{n+1}) $
- Euler explicite
  $ u_{n+1}=u_n+h\varphi(t_n,u_n) \quad\implies\quad p=0,\ a_0=1,\ b_{-1}=0,\ b_0=1; $
- Euler implicite
  $ u_{n+1}=u_n+h\varphi(t_{n+1},u_{n+1}) \quad\implies\quad p=0,\ a_0=1,\ b_{-1}=1,\ b_0=0; $
- Crank-Nicolson $ u_{n+1}=u_n+\frac{h}{2}\left(\varphi(t_n,u_n)+\varphi(t_{n+1},u_{n+1})\right) \quad\implies\quad p=0,\ a_0=1,\ b_{-1}=\frac{1}{2},\ b_0=\frac{1}{2}. $
Méthodes à $q\ge1$ pas
- Les méthodes $\text{AB}_q$, $\text{AM}_q$, $\text{N}_q$, $\text{MS}_q$ et $\text{BFD}_q$ sont toutes des méthodes numériques à $q=p+1$ étapes (=pas) linéaires.
NB Les méthodes EM et Heun ne rentrent pas dans ce cadre: elles sont des méthodes de la famille Runge-Kutta.

1 Polynômes caractéristiques

Dans cette partie nous allons étudier d’abord la convergence puis la A-stabilité d’une méthode multistep.

Dans l’analyse de ces méthodes, trois polynômes jouent un rôle clé. Pour cela, commençons par réécrire le schéma multistep comme suit: $ u_{n+1} -\sum_{j=0}^p a_ju_{n-j}= h\left(\sum_{j=0}^p b_j\varphi(t_{n-j},u_{n-j})+b_{-1}\varphi(t_{n+1},u_{n+1})\right). $

Définition.

Pour $r\in\mathbb{C}$, on associe à une méthode numérique linéaire multipas les trois polynômes caractéristiques suivants:

premier polynôme caractéristique $ \varrho(r)=r^{p+1}-\sum_{j=0}^p a_jr^{p-j} $
second polynôme caractéristique $ \sigma(r)=b_{-1}r^{p+1}+\sum_{j=0}^p b_jr^{p-j} $
polynôme de A-stabilité $ p_z(r) = \varrho(r) - z \sigma(r) $

Formellement,

pour construire le premier polynôme caractéristique on ne regarde que le LHS et les $u_{n-j}$ deviennent des $r^{p-j}$,
pour construire le second polynôme caractéristique on ne regarde que le RHS divisé par $h$ et les $\varphi(t_{n-j},u_{n-j})$ deviennent des $r^{p-j}$.

On verra que les racines du polynôme $\varrho$ sont liées à la zéro-stabilité tandis que celles du polynôme $p$ sont liées à la stabilité absolue (en association avec un choix particulier de $z=h\lambda$).

Exemples :

Euler explicite : $\varrho(r)=r-1$ et $\sigma(r)=1$
Euler implicite : $\varrho(r)=r-1$ et $\sigma(r)=r$
Crank-Nicolson : $\varrho(r)=r-1$ et $\sigma(r)=\frac{1}{2}r+\frac{1}{2}$
$\text{AB}_q$ ou $\text{AM}_q$ : $\varrho(r)=r^{q+1}-r^{q}=r^{q}(r-1)$
$\text{N}_q$ ou $\text{MS}_q$ : $\varrho(r)=r^{q+1}-r^{q-1}=r^{q-1}(r^2-1)$
$\text{BDF}_2$ : $\varrho(r)=r^2-\frac{4}{3}r+\frac{1}{3}=(r-1)\left(r-\frac{1}{3}\right)$ et $\sigma(r)=\frac{2}{3}$

2 Convergence d’un schéma multipas linéaire

Théorème (Dahlquist 1956).

Une méthode linéaire multipas est convergente si et seulement si elle est

1️⃣ consistante et
2️⃣ (zero)-stable.

2.1 1️⃣ Consistance

Une méthode est dite consistante si $\tau(h)=\max_n |\tau_n(h)|$ tend vers zéro quand $h$ tend vers zéro, où $\tau_n(h)$ est l’erreur de troncature locale de la méthode multi-pas définie par $ \tau_n(h)=\frac{1}{h}\left(y_{n+1}-\sum_{j=0}^p a_jy_{n-j}-h\sum_{j=0}^p b_j\varphi(t_{n-j},y_{n-j})-hb_{-1}\varphi(t_{n+1},y_{n+1})\right). $

Définition.

Pour $i=0,1,\dots$ introduisons la quantité $ \xi(i) = \sum_{j=0}^p (-j)^{i}a_j+i\sum_{j=-1}^p (-j)^{i-1}b_j, $ ayant posé $(-j)^0=1$ même pour $j=0$.

On a

$\xi(0)=\sum_{j=0}^p a_j$
$\xi(1)=\sum_{j=0}^p -j a_j+\sum_{j=-1}^p b_j$
$\xi(2)=\sum_{j=0}^p j^{2}a_j+2\sum_{j=-1}^p -j b_j$
$\xi(3)=\sum_{j=0}^p (-j)^{3}a_j+3\sum_{j=-1}^p j^{2}b_j$
$\dots$

Exemple avec un schéma à $q=4$ pas et donc $p=3$:

$\xi(0)=\Big(a_0+a_1+a_2+a_3\Big)$
$\xi(1)=-\Big(a_1+2a_2+3a_3\Big)+b_{-1}+\Big(b_1+b_2+b_3\Big)$
$\xi(2)=\Big(a_1+4a_2+9a_3\Big)+2b_{-1}-2\Big(b_1+2b_2+3b_3\Big)$
$\xi(3)=-\Big(a_1+8a_2+27a_3\Big)+3b_{-1}+3\Big(b_1+4b_2+9b_3\Big)$

Code

def xi_cond(p,omega):
    # j = 0...p # coeffs du schema
    # i = 0, ..., omega ordre du schema
    q = p+1
    display(Markdown(f"**Pour p={</span>p<span class="sc">} on a une méthode à q={</span>p<span class="op">+</span><span class="dv">1</span><span class="sc">} pas, on affiche ξ(i) pour i=0,...,{</span>omega<span class="sc">}**"))

    def xi(i):
        aa = sp.symbols(f'a_0:{</span>q<span class="sc">}')
        bb = sp.symbols(f'b_0:{</span>q<span class="sc">}')
        bm1 = sp.Symbol('b_{-1}')
        p = len(aa)
        sa = sum( [ (-j)**i * aa[j] for j in range(p) ] )
        sb = bm1+sum( [(-j)**(i-1) * bb[j] for j in range(1,p)] )
        # ??? si j=0 et i=0, il calcule (-j)**i =1 et on a bien a_0 dans la somme
        # mais si j=0 et i=1 il ne calcule pas b_0 et il faut l'ajouter à la main
        if i==1:
            sb += bb[0]
        return (sa).factor()+(i*sb).factor()

    for i in range(omega+1):
        display(Markdown(f"$\\xi({</span>i<span class="sc">}) = {</span>sp<span class="sc">.</span>latex(xi(i))<span class="sc">}$") )
    
# exemple
xi_cond(p=0,omega=5)

Pour p=0 on a une méthode à q=1 pas, on affiche ξ(i) pour i=0,…,5

$\xi(0) = a_{0}$

$\xi(1) = b_{0} + b_{-1}$

$\xi(2) = 2 b_{-1}$

$\xi(3) = 3 b_{-1}$

$\xi(4) = 4 b_{-1}$

$\xi(5) = 5 b_{-1}$

Par un développement de Taylor (assez fastidieux), on peut montrer que:

Proposition [consistance = ordre 1]

La méthode est consistante ssi $\xi(0)=\xi(1)=1$, autrement dit ssi $ \begin{cases} \displaystyle\sum_{j=0}^p a_j=1, \\ \displaystyle-\sum_{j=0}^p ja_j+\sum_{j=-1}^p b_j=1. \end{cases} $

Remarque: la première condition de consistance (i.e. $\xi(0)=1$) équivaut à $\varrho(1)=0$, la deuxième (i.e. $\xi(1)=1$) à $\varrho'(1)=\sigma(1)$.

Si, de plus, $\tau(h)=\mathscr{O}(Ch^\omega)$, on dit que la méthode est d’ordre $\omega$. Par des développements de Taylor, on peut montrer que la méthode est d’ordre $\omega$ ssi $\xi(0)=\xi(1)=\dots=\xi(\omega)=1$, autrement dit:

Proposition [ordre $>1$]

La méthode est d’ordre $\omega\ge2$ ssi $\xi(0)=\xi(1)=\dots=\xi(\omega)=1$, autrement dit ssi elle est consistante et, de plus, $ \sum_{j=0}^p (-j)^{i}a_j+i\sum_{j=-1}^p (-j)^{i-1}b_j=1 \quad i=2,\dots,\omega. $

Exemple: schéma $\text{AB}_2$

Schéma: $u_{n+1}=u_{n}+ \frac{h}{2} \big(3\varphi_{n}-\varphi_{n-1}\big)$
Coefficients: $q=2$, $p=1$, $a_0=1$, $a_1=0$, $b_0=\frac{3}{2}$, $b_1=-\frac{1}{2}$, $b_{-1}=0$
Consistance: $\begin{cases}\xi(0)=1+0=1\\\xi(1)=-(0a_0+1a_1)+(b_{-1}+b_0+b_1)=1\end{cases}$
Ordre $\omega$:
- pour $i=2$ on a $\xi(2)=a_1+2b_{-1}-2b_1=1$ donc $\omega\ge2$,
- pour $i=3$ on a $\xi(3)=-a_1+3b_{-1}+3b_1\neq1$ donc $\omega<3$
- on conclut que l’ordre $\omega$ est $2$

2.2 2️⃣ Zéro-stabilité

Proposition [zéro-stabilité et condition des racines]

Soient $r_0, r_1,\dots, r_p$ les $p+1$ racines du polynôme $\varrho$ (dans $\mathbb{C}$). On peut montrer que la méthode est zéro-stable ssi $ \begin{cases} |r_j|\le1 \quad\text{pour tout }j=0,\dots,p \\ r_j\text{ a multiplicité}>1\quad\implies \quad |r_j|<1. \end{cases} $

En particulier:

les méthodes à un pas (EE, EI, CN) vérifient $\varrho(r)=r-1$: le polynôme $\varrho$ n’a qu’une racine, c’est $r=1$. Toutes ces méthodes sont donc zéro-stables. On peut donc conclure que pour les méthodes à un pas, “consistance $=$ convergence”;
plus généralement, les méthodes de Adam à $q$ pas vérifient $\varrho(r)=r^{p+1}-r^p=r^p(r-1)$: il n’y a que deux racines, la racine $1$ de multiplicité $1$ et la racine $0$ de multiplicité $p$. Toutes ces méthodes sont donc zéro-stables, ici aussi on peut dire “consistance $=$ convergence”;
les méthodes de Nystrom et Milne-Simpson à $q$ pas vérifient $\varrho(r)=r^{p+1}-r^{p-1}=r^{p-1}(r-1)(r+1)$: il n’y a que trois racines, les racines $\pm1$ de multiplicité $1$ et la racine $0$ de multiplicité $p-1$. Toutes ces méthodes sont donc zéro-stables, ici aussi on peut dire “consistance $=$ convergence”;
enfin, on peut montrer que les méthodes BDF sont zéro-stables ssi $p\le4$ (et donc $q\le5$, voir les calculs sympy ci-dessous).

2.3 3️⃣ Ordre de convergence

La zero stabilité implique une restriction sur l’ordre atteignable pour une méthode multipas. On appelle cette contrainte la première barrière de Dahlquist :

Première barrière de Dahlquist [limitation de l’ordre]

L’ordre $\omega$ d’une méthode multipas à $q$ étapes convergente satisfait les inégalités suivantes: - si $b_{-1}=0$ (la méthode est explicite) alors $\omega\le q$ - si $b_{-1}\neq0$ (la méthode est implicite) on doit considérér deux cas - si $q$ est impair alors $\omega\le q+1$ - si $q$ est pair alors $\omega\le q+2$

Exemples :

Soit une méthode explicite ($b_{-1}=0$):
- si elle est à $q=1$ pas alors son ordre de consistance est au plus $\omega=q=1$; (exemple: $\text{AB}_1$=EE qui a ordre 1)
- si elle est à $q=2$ pas alors son ordre de consistance est au plus $\omega=q=2$; (exemple: $\text{AB}_2$ qui a ordre 2)
Soit une méthode implicite ($b_{-1}\neq0$):
- si elle est à $q=1$ pas alors son ordre de consistance est au plus $\omega=q+1=2$; (exemple: $\text{AM}_1$=CN qui a ordre 2)
  (Cas particulier: $\text{AM}_0$=EI est aussi à un pas mais avec notre notation on dirait à 0 pas et on trouve que l’ordre est $q+1=1$)
- si elle est à $q=2$ pas, alors son ordre de consistance est au plus $\omega=q+2=4$; (exemple: $\text{AM}_2$ qui a ordre 3 et $\text{MS}_2$ qui a ordre 4).

Code

# j = 0...p # coeffs du schema
# q = p+1 # nb de pas
# ω # ordre de la méthode

p = 3
q = p+1 
ordre_max = q+2 if q%2==0 else q+1

display(Markdown(f"**Pour une méthode à q={</span>q<span class="sc">} pas (et donc p={</span>p<span class="sc">})**"))
display(Markdown(f"Elle est d'ordre au plus {</span>ordre_max<span class="sc">}. Voici les conditions pour qu'elle soit d'ordre au moins 1, 2, ..., {</span>ordre_max<span class="sc">} :"))

aa = sp.symbols(f'a_0:{</span>q<span class="sc">}')
bb = sp.symbols(f'b_0:{</span>q<span class="sc">}')
bm1 = sp.Symbol('b_{-1}')

i = 1
sa = sum( [-j*aa[j] for j in range(len(aa))] )
sb = bm1+sum( [bb[j] for j in range(len(bb))] )
display(Markdown(f"- Pour que la méthode soit consistante (c'est-à-dire d'ordre au moins {</span>i<span class="sc">}) elle doit vérifier les deux conditions : "))
display(Markdown( "$" + sp.latex(sp.Eq( sum(aa).factor() , 1 ) ) + "$" ))
display(Markdown( "$" + sp.latex(sp.Eq( (sa).factor()+(i*sb).factor() , 1 ) ) + "$" ))

for i in range(2,ordre_max+1):
    sa = sum( [(-j)**i*aa[j] for j in range(len(aa))] )
    sb = bm1+sum( [(-j)**(i-1)*bb[j] for j in range(1,len(bb))] )
    display(Markdown(f"- Pour que la méthode soit d'ordre au moins {</span>i<span class="sc">} elle doit vérifier, en plus des précédentes, la condition : "))
    display(Markdown( "$" + sp.latex(sp.Eq( (sa).factor()+(i*sb).factor() , 1 ) ) + "$" ))

Pour une méthode à q=4 pas (et donc p=3)

Elle est d’ordre au plus 6. Voici les conditions pour qu’elle soit d’ordre au moins 1, 2, …, 6 :

Pour que la méthode soit consistante (c’est-à-dire d’ordre au moins 1) elle doit vérifier les deux conditions :

$a_{0} + a_{1} + a_{2} + a_{3} = 1$

$- a_{1} - 2 a_{2} - 3 a_{3} + b_{0} + b_{1} + b_{2} + b_{3} + b_{-1} = 1$

Pour que la méthode soit d’ordre au moins 2 elle doit vérifier, en plus des précédentes, la condition :

$a_{1} + 4 a_{2} + 9 a_{3} - 2 \left(b_{1} + 2 b_{2} + 3 b_{3} - b_{-1}\right) = 1$

Pour que la méthode soit d’ordre au moins 3 elle doit vérifier, en plus des précédentes, la condition :

$- a_{1} - 8 a_{2} - 27 a_{3} + 3 \left(b_{1} + 4 b_{2} + 9 b_{3} + b_{-1}\right) = 1$

Pour que la méthode soit d’ordre au moins 4 elle doit vérifier, en plus des précédentes, la condition :

$a_{1} + 16 a_{2} + 81 a_{3} - 4 \left(b_{1} + 8 b_{2} + 27 b_{3} - b_{-1}\right) = 1$

Pour que la méthode soit d’ordre au moins 5 elle doit vérifier, en plus des précédentes, la condition :

$- a_{1} - 32 a_{2} - 243 a_{3} + 5 \left(b_{1} + 16 b_{2} + 81 b_{3} + b_{-1}\right) = 1$

Pour que la méthode soit d’ordre au moins 6 elle doit vérifier, en plus des précédentes, la condition :

$a_{1} + 64 a_{2} + 729 a_{3} - 6 \left(b_{1} + 32 b_{2} + 243 b_{3} - b_{-1}\right) = 1$

Récapitulatif des méthodes multipas vues jusqu’ici:

Code

sc = { <span class="st">"EE = AB_1"</span> : { <span class="st">"aa"</span>:[<span class="dv">1</span>], <span class="st">"bb"</span>:[ <span class="dv">1</span>], <span class="st">"bm1"</span>:<span class="dv">0</span>  },
       "EI = AM_0 = BDF_1" : { <span class="st">"aa"</span>:[<span class="dv">1</span>], <span class="st">"bb"</span>:[ <span class="dv">0</span>], <span class="st">"bm1"</span>:<span class="dv">1</span>  },
       "CN = AM_1" : { <span class="st">"aa"</span>:[<span class="dv">1</span>], <span class="st">"bb"</span>:[sp.Rational(<span class="dv">1</span>,<span class="dv">2</span>)], <span class="st">"bm1"</span>:<span class="dv">1</span><span class="op">/</span><span class="dv">2</span>  }, 
       "AB_2": { <span class="st">"aa"</span>:[<span class="dv">1</span>,<span class="dv">0</span>], <span class="st">"bb"</span>:[sp.Rational(<span class="dv">3</span>,<span class="dv">2</span>),sp.Rational(<span class="op">-</span><span class="dv">1</span>,<span class="dv">2</span>)], <span class="st">"bm1"</span>:<span class="dv">0</span>  }, 
       "AB_3": { <span class="st">"aa"</span>:[<span class="dv">1</span>,<span class="dv">0</span>,<span class="dv">0</span>], <span class="st">"bb"</span>:[sp.Rational(<span class="dv">23</span>,<span class="dv">12</span>),sp.Rational(<span class="op">-</span><span class="dv">16</span>,<span class="dv">12</span>), sp.Rational(<span class="dv">5</span>,<span class="dv">12</span>)], <span class="st">"bm1"</span>:<span class="dv">0</span>  }, 
       "AB_4": { <span class="st">"aa"</span>:[<span class="dv">1</span>,<span class="dv">0</span>,<span class="dv">0</span>,<span class="dv">0</span>], <span class="st">"bb"</span>:[sp.Rational(<span class="dv">55</span>,<span class="dv">24</span>),sp.Rational(<span class="op">-</span><span class="dv">59</span>,<span class="dv">24</span>), sp.Rational(<span class="dv">37</span>,<span class="dv">24</span>), sp.Rational(<span class="op">-</span><span class="dv">9</span>,<span class="dv">24</span>)], <span class="st">"bm1"</span>:<span class="dv">0</span>  }, 
       "AB_5": { <span class="st">"aa"</span>:[<span class="dv">1</span>,<span class="dv">0</span>,<span class="dv">0</span>,<span class="dv">0</span>,<span class="dv">0</span>], <span class="st">"bb"</span>:[sp.Rational(<span class="dv">1901</span>,<span class="dv">720</span>), sp.Rational(<span class="op">-</span><span class="dv">2774</span>,<span class="dv">720</span>), sp.Rational(<span class="dv">2616</span>,<span class="dv">720</span>), sp.Rational(<span class="op">-</span><span class="dv">1274</span>,<span class="dv">720</span>), sp.Rational(<span class="dv">251</span>,<span class="dv">720</span>)], <span class="st">"bm1"</span>:<span class="dv">0</span>  }, 
       "AM_2": { <span class="st">"aa"</span>:[<span class="dv">1</span>,<span class="dv">0</span>], <span class="st">"bb"</span>:[sp.Rational(<span class="dv">8</span>,<span class="dv">12</span>),sp.Rational(<span class="op">-</span><span class="dv">1</span>,<span class="dv">12</span>)], <span class="st">"bm1"</span>:sp.Rational(<span class="dv">5</span>,<span class="dv">12</span>)  }, 
       "AM_3": { <span class="st">"aa"</span>:[<span class="dv">1</span>,<span class="dv">0</span>,<span class="dv">0</span>], <span class="st">"bb"</span>:[sp.Rational(<span class="dv">19</span>,<span class="dv">24</span>),sp.Rational(<span class="op">-</span><span class="dv">5</span>,<span class="dv">24</span>),sp.Rational(<span class="dv">1</span>,<span class="dv">24</span>)], <span class="st">"bm1"</span>:sp.Rational(<span class="dv">9</span>,<span class="dv">24</span>)  }, 
       "AM_4": { <span class="st">"aa"</span>:[<span class="dv">1</span>,<span class="dv">0</span>,<span class="dv">0</span>,<span class="dv">0</span>], <span class="st">"bb"</span>:[sp.Rational(<span class="dv">646</span>,<span class="dv">720</span>),sp.Rational(<span class="op">-</span><span class="dv">264</span>,<span class="dv">720</span>),sp.Rational(<span class="dv">106</span>,<span class="dv">720</span>),sp.Rational(<span class="op">-</span><span class="dv">19</span>,<span class="dv">720</span>)], <span class="st">"bm1"</span>:sp.Rational(<span class="dv">251</span>,<span class="dv">720</span>) }, 
       "BDF_2": { <span class="st">"aa"</span>:[sp.Rational(<span class="dv">4</span>,<span class="dv">3</span>),sp.Rational(<span class="op">-</span><span class="dv">1</span>,<span class="dv">3</span>)], <span class="st">"bb"</span>:[<span class="dv">0</span>,<span class="dv">0</span>], <span class="st">"bm1"</span>:sp.Rational(<span class="dv">2</span>,<span class="dv">3</span>) }, 
       "BDF_3": { <span class="st">"aa"</span>:[sp.Rational(<span class="dv">18</span>,<span class="dv">11</span>),sp.Rational(<span class="op">-</span><span class="dv">9</span>,<span class="dv">11</span>),sp.Rational(<span class="dv">2</span>,<span class="dv">11</span>)], <span class="st">"bb"</span>:[<span class="dv">0</span>,<span class="dv">0</span>,<span class="dv">0</span>], <span class="st">"bm1"</span>:sp.Rational(<span class="dv">6</span>,<span class="dv">11</span>) }, 
       "BDF_4": { <span class="st">"aa"</span>:[sp.Rational(<span class="dv">48</span>,<span class="dv">25</span>),sp.Rational(<span class="op">-</span><span class="dv">36</span>,<span class="dv">25</span>),sp.Rational(<span class="dv">16</span>,<span class="dv">25</span>),sp.Rational(<span class="op">-</span><span class="dv">3</span>,<span class="dv">25</span>)], <span class="st">"bb"</span>:[<span class="dv">0</span>,<span class="dv">0</span>,<span class="dv">0</span>,<span class="dv">0</span>], <span class="st">"bm1"</span>:sp.Rational(<span class="dv">12</span>,<span class="dv">25</span>) }, 
       "BDF_5": { <span class="st">"aa"</span>:[sp.Rational(<span class="dv">300</span>,<span class="dv">137</span>),sp.Rational(<span class="op">-</span><span class="dv">300</span>,<span class="dv">137</span>),sp.Rational(<span class="dv">200</span>,<span class="dv">137</span>),sp.Rational(<span class="op">-</span><span class="dv">75</span>,<span class="dv">137</span>),sp.Rational(<span class="dv">12</span>,<span class="dv">137</span>)], <span class="st">"bb"</span>:[<span class="dv">0</span>,<span class="dv">0</span>,<span class="dv">0</span>,<span class="dv">0</span>,<span class="dv">0</span>], <span class="st">"bm1"</span>:sp.Rational(<span class="dv">60</span>,<span class="dv">137</span>) }, 
       "BDF_6": { <span class="st">"aa"</span>:[sp.Rational(<span class="dv">120</span>,<span class="dv">49</span>),sp.Rational(<span class="op">-</span><span class="dv">150</span>,<span class="dv">49</span>),sp.Rational(<span class="dv">400</span>,<span class="dv">147</span>),sp.Rational(<span class="op">-</span><span class="dv">75</span>,<span class="dv">49</span>),sp.Rational(<span class="dv">24</span>,<span class="dv">49</span>),sp.Rational(<span class="op">-</span><span class="dv">10</span>,<span class="dv">147</span>)], <span class="st">"bb"</span>:[<span class="dv">0</span>,<span class="dv">0</span>,<span class="dv">0</span>,<span class="dv">0</span>,<span class="dv">0</span>,<span class="dv">0</span>], <span class="st">"bm1"</span>:sp.Rational(<span class="dv">20</span>,<span class="dv">49</span>) }, 
       "MS_2": { <span class="st">"aa"</span>:[<span class="dv">0</span>,<span class="dv">1</span>], <span class="st">"bb"</span>:[sp.Rational(<span class="dv">4</span>,<span class="dv">3</span>),sp.Rational(<span class="dv">1</span>,<span class="dv">3</span>)], <span class="st">"bm1"</span>:sp.Rational(<span class="dv">1</span>,<span class="dv">3</span>) }
       } 

sp.var('r')

for schema in sc.keys():
    display(Markdown(f"**{</span>schema<span class="sc">}**"))      
    q = len(sc[schema]["aa"])
    p = q-1
    display(Markdown(f" - Schéma à {</span>q <span class="op">=</span> <span class="sc">} pas"))
    aa = sc[schema]["aa"]
    bb = sc[schema]["bb"]
    bm1 = sc[schema]["bm1"]
    
    if bm1==0:
        display(Markdown(f"- Le schéma est explicite car $b_{</span><span class="op">-</span><span class="dv">1</span><span class="sc">}=0$."))
    else:
        display(Markdown(f"- Le schéma est implicite car $b_{</span><span class="op">-</span><span class="dv">1</span><span class="sc">}={</span>bm1<span class="sc">}$."))
    
    ordre = []
    ordre.append( sum(aa)==1 and sum([-j*aa[j] for j in range(len(aa))])+bm1+sum(bb)==1  )
    # print("\tConsistance: ",end="")
    # print(ordre[-1])
    display(Markdown(f"- Consistance: {</span>ordre[<span class="op">-</span><span class="dv">1</span>]<span class="sc">}"))

    i=1
    while ordre[-1]:
        i += 1
        ordre.append( sum([(-j)**i*aa[j]+i*(-j)**(i-1)*bb[j] for j in range(len(aa))])+i*bm1==1)
    # print(f"\tOrdre {len(ordre)-1}")
    display(Markdown(f"- Ordre {</span><span class="bu">len</span>(ordre)<span class="op">-</span><span class="dv">1</span><span class="sc">}"))    
    
    rho = np.array([1])
    rho = np.append(rho,-np.array(aa))
    rho_sp = sp.Poly(rho,r).as_expr()
    # display(Math(r'\varrho(r)='+sp.latex(sp.expand(poly1d(rho)(r)))))
    display(Markdown(f"- Polynome: $\\varrho(r) = {</span>sp<span class="sc">.</span>latex(rho_sp)<span class="sc">}$"))
#     print(f"\tZéro-stabilité: |r_j|= {abs(roots(rho))}")
#     print("\tRacines: ",end="")
#     display(sp.solve(sp.expand(poly1d(rho)(r))))
    display(Markdown(f"- Ensemble des modules des racines : "))
    display( Math(r' \{|r_j|\} = '+sp.latex( [abs(rac).simplify().evalf() for rac in sp.solve(rho_sp)]  )))

EE = AB_1

Schéma à q = 1 pas

Le schéma est explicite car $b_-1=0$.

Consistance: True

Ordre 1

Polynome: $\varrho(r) = r - 1$

Ensemble des modules des racines :

$\displaystyle \{|r_j|\} = \left[ 1.0\right]$

EI = AM_0 = BDF_1

Schéma à q = 1 pas

Le schéma est implicite car $b_-1=1$.

Consistance: True

Ordre 1

Polynome: $\varrho(r) = r - 1$

Ensemble des modules des racines :

$\displaystyle \{|r_j|\} = \left[ 1.0\right]$

CN = AM_1

Schéma à q = 1 pas

Le schéma est implicite car $b_-1=0.5$.

Consistance: True

Ordre 2

Polynome: $\varrho(r) = r - 1$

Ensemble des modules des racines :

$\displaystyle \{|r_j|\} = \left[ 1.0\right]$

AB_2

Schéma à q = 2 pas

Le schéma est explicite car $b_-1=0$.

Consistance: True

Ordre 2

Polynome: $\varrho(r) = r^{2} - r$

Ensemble des modules des racines :

$\displaystyle \{|r_j|\} = \left[ 0, \ 1.0\right]$

AB_3

Schéma à q = 3 pas

Le schéma est explicite car $b_-1=0$.

Consistance: True

Ordre 3

Polynome: $\varrho(r) = r^{3} - r^{2}$

Ensemble des modules des racines :

$\displaystyle \{|r_j|\} = \left[ 0, \ 1.0\right]$

AB_4

Schéma à q = 4 pas

Le schéma est explicite car $b_-1=0$.

Consistance: True

Ordre 4

Polynome: $\varrho(r) = r^{4} - r^{3}$

Ensemble des modules des racines :

$\displaystyle \{|r_j|\} = \left[ 0, \ 1.0\right]$

AB_5

Schéma à q = 5 pas

Le schéma est explicite car $b_-1=0$.

Consistance: True

Ordre 5

Polynome: $\varrho(r) = r^{5} - r^{4}$

Ensemble des modules des racines :

$\displaystyle \{|r_j|\} = \left[ 0, \ 1.0\right]$

AM_2

Schéma à q = 2 pas

Le schéma est implicite car $b_-1=5/12$.

Consistance: True

Ordre 3

Polynome: $\varrho(r) = r^{2} - r$

Ensemble des modules des racines :

$\displaystyle \{|r_j|\} = \left[ 0, \ 1.0\right]$

AM_3

Schéma à q = 3 pas

Le schéma est implicite car $b_-1=3/8$.

Consistance: True

Ordre 4

Polynome: $\varrho(r) = r^{3} - r^{2}$

Ensemble des modules des racines :

$\displaystyle \{|r_j|\} = \left[ 0, \ 1.0\right]$

AM_4

Schéma à q = 4 pas

Le schéma est implicite car $b_-1=251/720$.

Consistance: True

Ordre 5

Polynome: $\varrho(r) = r^{4} - r^{3}$

Ensemble des modules des racines :

$\displaystyle \{|r_j|\} = \left[ 0, \ 1.0\right]$

BDF_2

Schéma à q = 2 pas

Le schéma est implicite car $b_-1=2/3$.

Consistance: True

Ordre 2

Polynome: $\varrho(r) = r^{2} - \frac{4 r}{3} + \frac{1}{3}$

Ensemble des modules des racines :

$\displaystyle \{|r_j|\} = \left[ 0.333333333333333, \ 1.0\right]$

BDF_3

Schéma à q = 3 pas

Le schéma est implicite car $b_-1=6/11$.

Consistance: True

Ordre 3

Polynome: $\varrho(r) = r^{3} - \frac{18 r^{2}}{11} + \frac{9 r}{11} - \frac{2}{11}$

Ensemble des modules des racines :

$\displaystyle \{|r_j|\} = \left[ 1.0, \ 0.426401432711221, \ 0.426401432711221\right]$

BDF_4

Schéma à q = 4 pas

Le schéma est implicite car $b_-1=12/25$.

Consistance: True

Ordre 4

Polynome: $\varrho(r) = r^{4} - \frac{48 r^{3}}{25} + \frac{36 r^{2}}{25} - \frac{16 r}{25} + \frac{3}{25}$

Ensemble des modules des racines :

$\displaystyle \{|r_j|\} = \left[ 1.0, \ 0.56086151609339, \ 0.56086151609339, \ 0.38147840911841\right]$

BDF_5

Schéma à q = 5 pas

Le schéma est implicite car $b_-1=60/137$.

Consistance: True

Ordre 5

Polynome: $\varrho(r) = r^{5} - \frac{300 r^{4}}{137} + \frac{300 r^{3}}{137} - \frac{200 r^{2}}{137} + \frac{75 r}{137} - \frac{12}{137}$

Ensemble des modules des racines :

$\displaystyle \{|r_j|\} = \left[ 1.0, \ 0.708710816266406, \ 0.417600758175733, \ 0.708710816266406, \ 0.417600758175733\right]$

BDF_6

Schéma à q = 6 pas

Le schéma est implicite car $b_-1=20/49$.

Consistance: True

Ordre 6

Polynome: $\varrho(r) = r^{6} - \frac{120 r^{5}}{49} + \frac{150 r^{4}}{49} - \frac{400 r^{3}}{147} + \frac{75 r^{2}}{49} - \frac{24 r}{49} + \frac{10}{147}$

Ensemble des modules des racines :

$\displaystyle \{|r_j|\} = \left[ 1.0, \ 0.40612326685391, \ 0.474034857706592, \ 0.474034857706592, \ 0.863380267869827, \ 0.863380267869827\right]$

MS_2

Schéma à q = 2 pas

Le schéma est implicite car $b_-1=1/3$.

Consistance: True

Ordre 4

Polynome: $\varrho(r) = r^{2} - 1$

Ensemble des modules des racines :

$\displaystyle \{|r_j|\} = \left[ 1.0, \ 1.0\right]$

2.4 Méthodes cycliques composites

On peut surmonter les limites imposées par les barrières de Dahlquist en combinant plusieurs méthodes multi-pas. Par exemple, les deux méthodes suivantes $ \begin{align*} u_{n+1} &= -\frac{8}{11}u_{n} + \frac{19}{11}u_{n-1} + \frac{h}{30} \big( 30\varphi_{n+1}+57\varphi_n+24\varphi_{n-1}-\varphi_{n-2} \big) \\ u_{n+1} &= \frac{449}{240}u_{n} - \frac{19}{30}u_{n-1} -\frac{361}{240}u_{n-2} + \frac{h}{720}\big(251\varphi_{n+1}+456\varphi_n-1347\varphi_{n-1}-350\varphi_{n-2}\big) \end{align*} $ sont d’ordre cinq, mais sont instables. Cependant, en les combinant (la première si $n$ est pair, la deuxième si $n$ est impair), elles définissent une méthode A-stable à trois pas d’ordre cinq.

3 A-stabilité (dans $\mathbb{C}$)

La première barrière de Dalquist affirme qu’on peut augmenter arbitrairement l’ordre d’un schéma multipas en augmentant le nombre de pas. La convergence dépend ensuite juste du premier polynôme caractéristique. Cependant, dans la section précédente, on a considéré la résolution du problème de Cauchy sur des intervalles bornés et la convergence suppose $h\to0$.

Il existe tutefois de nombreuses situations dans lesquelles le problème de Cauchy doit être intégré sur des intervalles en temps très grands ou même infini. Dans ce cas, même pour $h$ fixé, $N$ tend vers l’infini, et un résultat comme la zéro-stabilité n’a plus de sens puisque le membre de droite contient lq quantité non bornée ($T-t_0$).
On s’intéresse donc à des méthodes capables d’approcher la solution pour des intervalles en temps arbitrairement grands, même pour des pas de temps $h$ “assez grands”.

Soit $\lambda\in\mathbb{C}$ un nombre complexe tel que $\Re(\lambda)=-\beta<0$ et considérons le problème de Cauchy $\begin{cases} y'(t)=\lambda y(t), &\text{pour }t>0,\\ y(0)=1 \end{cases}$ Sa solution est $y(t)=e^{\lambda t}$ et comme $\Re(\lambda)<0$ alors $\lim_{t\to+\infty}|y(t)|=0.$

Soit $h>0$ un pas de temps donné, $t_n=nh$ pour $n\in\mathbb{N}$ et notons $u_n\approx y(t_n)$ une approximation de la solution $y$ au temps $t_n$.

Si, sous d’éventuelles conditions sur $h$, on a $ \lim_{n\to+\infty} |u_n| =0,$ alors on dit que le schéma est A-stable (absolument stable).

3.1 Région de A-stabilité (dans $\mathbb{C}$)

On appelle région de stabilité absolue $A$ d’une méthode numérique l’ensemble des nombres complexes $z = h\lambda$ pour lesquels la méthode est absolument stable : $ A=\Big\{z = h\lambda \in \mathbb{C} \ \Big| \ |u_n|\xrightarrow[n\to+\infty]{}0 \Big\} $ Une méthode numérique est inconditionellement A-stable si $\mathbb{C}^-\subset A$ où $\mathbb{C}^-=\{z\in\mathbb{C}|\Re(z)<0\}$.

Une méthode à $q=p+1$ pas appliquée à ce problème modèle conduit à l’équation récurrente à $ u_{n+1}=\sum_{j=0}^p a_j u_{n-j} + z \sum_{j=0}^p b_ju_{n-j} + z b_{-1}u_{n+1} $

Condition des racines stricte : une méthode multipas linéaire vérifie la condition des racines stricte (éventuellement sous conditions sur $h$) si les racines du polynôme $p$ sont dans le disque unité ouvert de $\mathbb{C}$:

$ \text{il existe $h_0>0$ tel que }\quad |r_j(z)|<1 \quad\text{pour tout }j=0,\dots,p;\ \forall h\le h_0 $

Proposition : une méthode multipas linéaire est absolument stable si et seulement si son polynôme de stabilité vérifie la condition des racines stricte.

Deuxième barrière de Dahlquist [Le 🎅 n’existe pas … borne sur $h$]

Il n’existe pas de méthode multipas explicite inconditionellement A-stable.
Il n’existe pas de méthode multipas implicite d’ordre $>2$ inconditionellement A-stable.

Autrement dit : augmenter le nombre de pas permet d’augment l’ordre de convergence mais cela va de pair avec une restriction sur la taille du pas.

Conséquences :

Tous les schémas $\text{AB}_q$ ont une condition de A-stabilité.
Exemple : pour le schéma $\text{AB}_1$ (Euler explicite) $p(r)=(r-1)-z$. Il a une seule racine : $r=1+z$. On demande à ce que $|1+z|<1$. On obtient dans $\mathbb{C}$ le cercle (ouvert) de centre $(-1,0)$ et rayon $1$. Si on considère le cas réel, c.-à-d. $\varphi(t,y)=\beta y$ avec $\beta=-\Re(\lambda)$, la condition devient $0<\beta h<1$ comme nous avons déjà trouvé lors du cours CM-4.
Les schémas $\text{AM}_q$ avec $q>1$ ont une condition de A-stabilité.
Exemple : pour le schéma $\text{AM}_0$ (Euler implicite) $p(r)=(r-1)-zr$. Il a une seule racine : $r=\frac{1}{1+z}$. On demande à ce que $\left|\frac{1}{1+z}\right|<1$. On obtient dans $\mathbb{C}$ la partie extérieure du cercle (fermé) de centre $(1,0)$ et rayon $1$. Comme $\mathbb{C}^-$ est contenu dans cette région, la méthode est inconditionnellement A-stable.
Exemple : pour le schéma $\text{AM}_1$ (Crank-Nicolson) $p(r)=(r-1)-z\frac{1}{2}(r+1)$. Il a une seule racine : $r=\frac{2+z}{2-z}$. On demande à ce que $\left|\frac{2+z}{2-z}\right|<1$. On obtient dans $\Re(z)<1$. Comme $\mathbb{C}^-$ est contenu de cette région, la méthode est inconditionnellement A-stable.

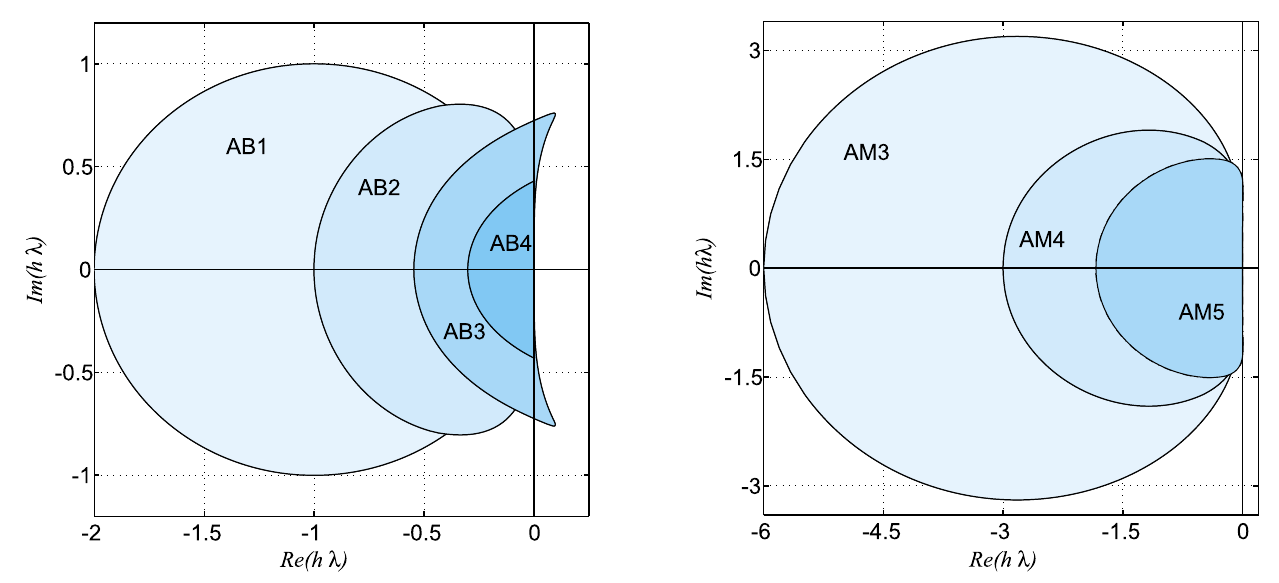
Régions de A-stabilité de diverses méthodes d’Adams-Bashforth (à gauche) et d’Adams-Moulton (à droite).
Source: A. Quarteroni, F. Saleri, P. Gervasio Calcul Scientifique: Cours, exercices corrigés et illustrations en Matlab et Octave.

On remarque que les régions de stabilité absolue des méthodes d’Adams-Bashforth et d’Adams-Moulton sont bornées et diminuent quand l’ordre augmente. Si on cherche des méthodes avec un ordre de convergence supérieur à 2, ils ne sont pas adaptés pour résoudre des problèmes de Cauchy sur des intervalles de temps très longs car ils ne sont pas inconditionnellement A-stables.

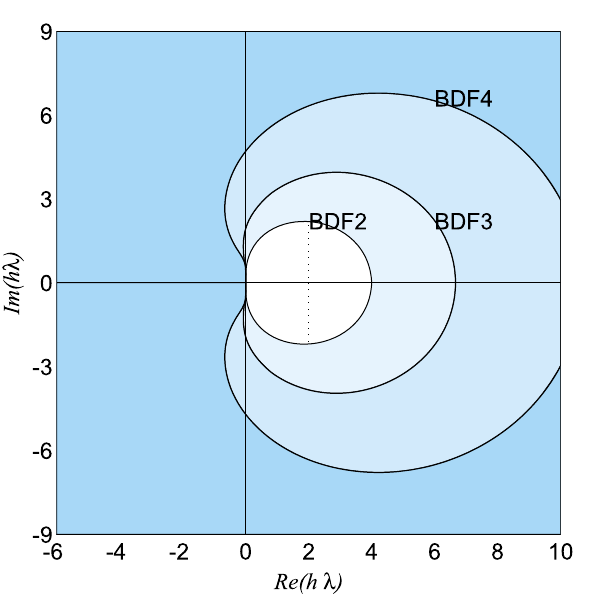
Régions de A-stabilité de diverses méthodes BDF.
Source: A. Quarteroni, F. Saleri, P. Gervasio Calcul Scientifique: Cours, exercices corrigés et illustrations en Matlab et Octave.

On remarque que les régions de stabilité absolue des méthodes BDF, pour $q\le6$, sont non bornées. En particulier, elles contiennent toujours les réels négatifs, ce qui fait qu’ils sont très utlisés pour résoudre des problèmes de Cauchy sur des intervalles en temps très grands ou même infini ou des problèmes raides.

Tracer les régions de A-stabilité.
Posons $z=h\lambda$. Il est en général difficile de déterminer la région de stabilité absolue car on doit décider pour quels $z\in\mathbb{C}$ les racines du polynôme de stabilité vérifient la condition de racines stricte (i.e. $|r| < 1$). Il est plus aisé de déterminer la frontière de cette région car au moins une des racines de $p$ à la frontière est de module $1$. On a donc $|r| = 1$ sur $\partial A$. La frontière de $A$ est alors un sous ensemble des points $z\in\mathbb{C}$ pour lesquels $r=e^{i\vartheta}$, $\vartheta\in\mathbb{R}$. On remplace alors $r =e^{i\vartheta}$ dans $p$ et comme $e^{i\vartheta}$ est racine, $p(e^{i\vartheta}) = 0$ et on résoud l’équation. On obtient $z = z(\vartheta)$ ce qui donne une courbe dans $\mathbb{C}$ en fonction de l’angle $\vartheta$, ce qui décrit donc une courbe polaire. Par conséquent, pour obtenir une représentation approchée de $\partial A$, il suffit d’évaluer le second membre pour diverses valeurs de $r$ sur le cercle unité, diverses valeurs de $\vartheta\in\mathbb{R}$ et $r=e^{i\vartheta}$.

Code

def polyCar(schema):
    sp.var('r z')
    p,aa,bb,bm1=schema["p"],schema["aa"],schema["bb"],schema["bm1"]   
    rho = r**(p+1)-sum(aa[j]*r**(p-j)for j in range(p+1))    
    sigma = bm1*r**(p+1)+sum(bb[j]*r**(p-j)for j in range(p+1))
    display(Math(r'\varrho(r)='+sp.latex(rho)))
    display(Math(r'\sigma(r)='+sp.latex(sigma)))
    

def polyCarIMPL(schema):
    sp.var('r z')
    p,aa,bb,bm1=schema["p"],schema["aa"],schema["bb"],schema["bm1"]  
    rho=r**(p+1)-sum(aa[j]*r**(p-j)for j in range(p))    
    sigma=bm1*r**(p+1)+sum(bb[j]*r**(p-j)for j in range(p))
    display(Math(r'\varrho(r)='+sp.latex(rho)))
    display(Math(r'\sigma(r)='+sp.latex(sigma)))
    
    

# Returns > 1 if argument is not in region of absolute stability
def stabilityFunction(z,schema):
    schema["aa"] = [float(a) for a in schema["aa"]]
    schema["bb"] = [float(b) for b in schema["bb"]]
    schema["bm1"] = float(schema["bm1"])
    pol = np.array(schema["aa"])+z*np.array(schema["bb"])
    pol = np.append([1-z*schema["bm1"]],-pol)
    return max(abs(np.roots(pol)))


def Astabilite(schema):
    schema["aa"] = [float(a) for a in schema["aa"]]
    schema["bb"] = [float(b) for b in schema["bb"]]
    schema["bm1"] = float(schema["bm1"])
    p,aa,bb,bm1=schema["p"],schema["aa"],schema["bb"],schema["bm1"]
    
    # cc liste de points sur le circle unitaire
    rr = np.linspace(0,2*np.pi,201)
    cc = np.cos(rr)+1j*np.sin(rr) 
    ## ff fonction vectorisée qui donne zz
    ff = lambda cc,p,aa,bb,bm1 : (cc**(p+1)-np.polyval(aa,cc))/(bm1*cc**(p+1)+np.polyval(bb,cc)) 
    zz = ff(cc,p,aa,bb,bm1)
    
    plt.figure(figsize=(18,7))
    plt.subplot(1,2,1)
    plt.plot(zz.real,zz.imag,'r')
    plt.grid(True)
#     plt.axis('equal')
    plt.xlabel(r'$\Re(h\lambda)$')
    plt.ylabel(r'$\Im(h\lambda)$');
    plt.title(schema["Nom"])
    Lx,Ly = plt.xlim(),plt.ylim()
    
    plt.subplot(1,2,2)
    x = np.linspace(Lx[0],Lx[1], 300)
    y = np.linspace(Ly[0],Ly[1], 300)
    [X,Y] = np.meshgrid(x,y)
    Z = np.zeros(X.shape)
    for m in range(X.shape[0]):
        for n in range(X.shape[1]):
            Z[m,n] = stabilityFunction(X[m,n] + 1j * Y[m,n], schema)
    plt.contour(X, Y, Z, [1], colors='k')
    plt.contourf(X, Y, Z, [0,1], colors=[[1, 0.5, 0.8]])
    return None

Code

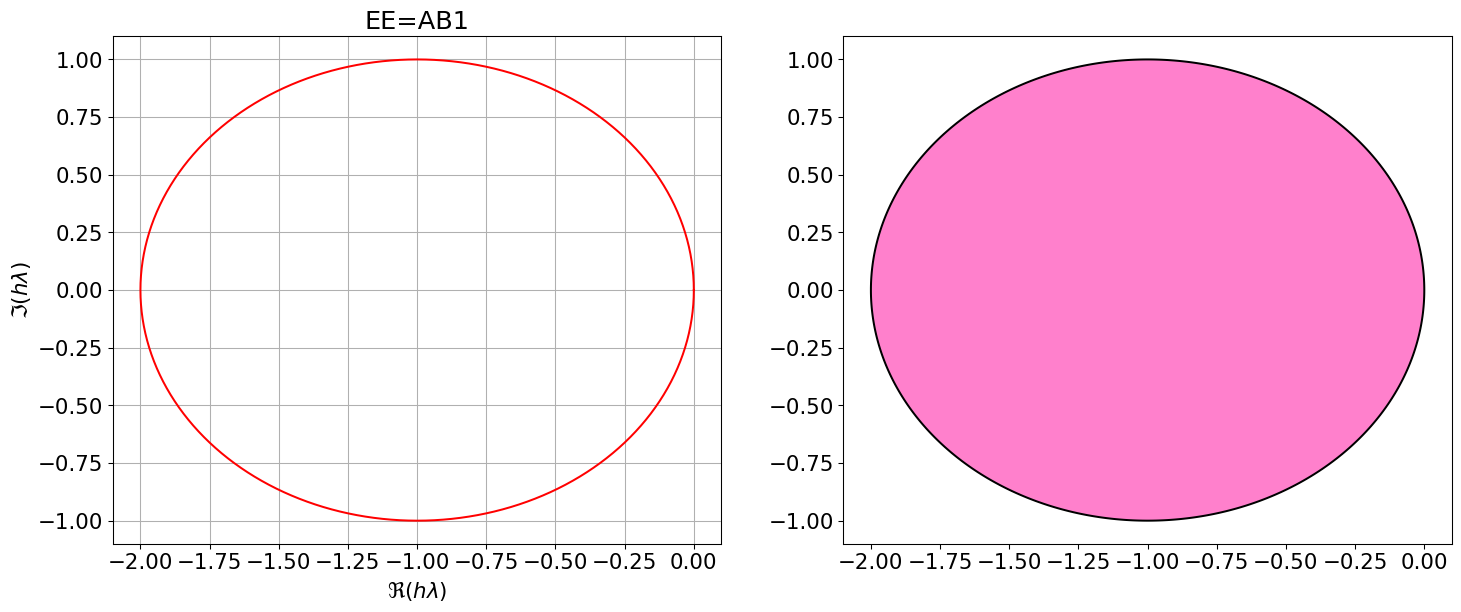
EE = { <span class="st">"Nom"</span>:<span class="st">"EE=AB1"</span>, <span class="st">"p"</span>:<span class="dv">0</span>, <span class="st">"aa"</span>:[<span class="dv">1</span>], <span class="st">"bb"</span>:[<span class="dv">1</span>], <span class="st">"bm1"</span>:<span class="dv">0</span>  }
polyCar(EE)
Astabilite(EE)

$\displaystyle \varrho(r)=r - 1$

$\displaystyle \sigma(r)=1$

Code

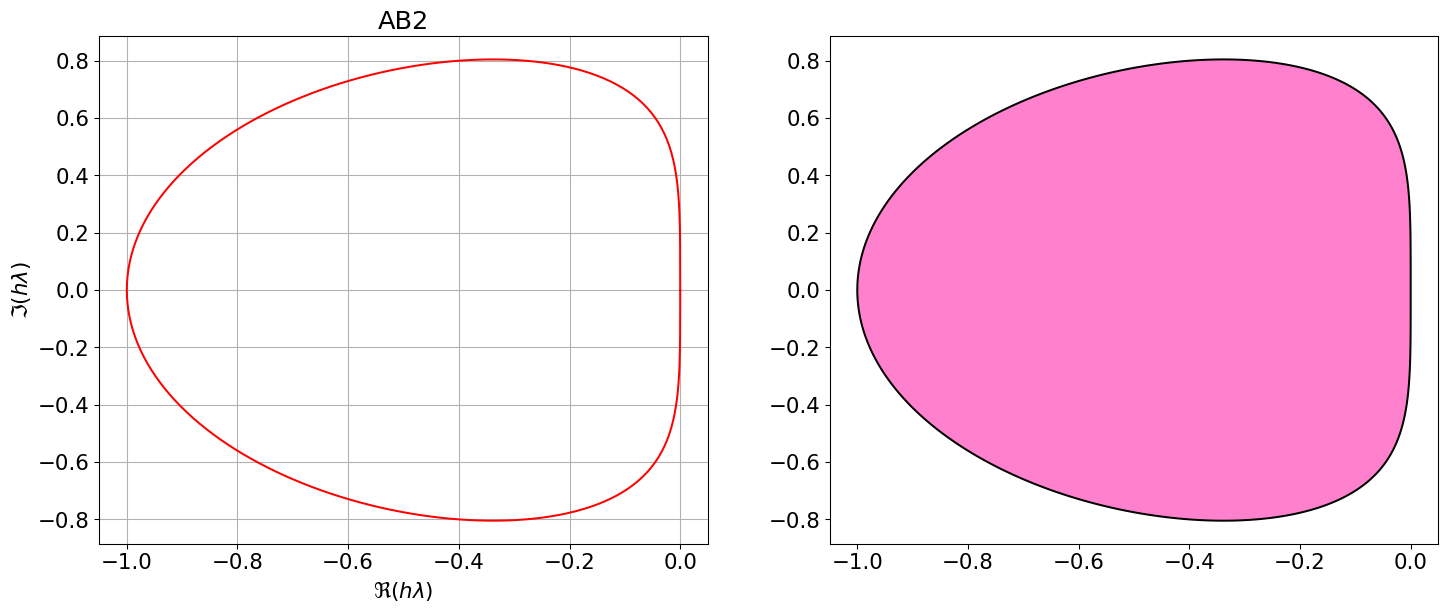
AB2 = { <span class="st">"Nom"</span>:<span class="st">"AB2"</span>, <span class="st">"p"</span>:<span class="dv">1</span>, <span class="st">"aa"</span>:[<span class="dv">1</span>,<span class="dv">0</span>], <span class="st">"bb"</span>:[sp.Rational(<span class="dv">3</span>,<span class="dv">2</span>),<span class="op">-</span>sp.Rational(<span class="dv">1</span>,<span class="dv">2</span>)], <span class="st">"bm1"</span>:<span class="dv">0</span>  }
polyCar(AB2)
Astabilite(AB2)

$\displaystyle \varrho(r)=r^{2} - r$

$\displaystyle \sigma(r)=\frac{3 r}{2} - \frac{1}{2}$

Code

AB3 = { <span class="st">"Nom"</span>:<span class="st">"AB3"</span>, <span class="st">"p"</span>:<span class="dv">2</span>, <span class="st">"aa"</span>:[<span class="dv">1</span>,<span class="dv">0</span>,<span class="dv">0</span>], <span class="st">"bb"</span>:[sp.Rational(<span class="dv">23</span>,<span class="dv">12</span>),<span class="op">-</span>sp.Rational(<span class="dv">16</span>,<span class="dv">12</span>), sp.Rational(<span class="dv">5</span>,<span class="dv">12</span>)], <span class="st">"bm1"</span>:<span class="dv">0</span>  }
polyCar(AB3)
Astabilite(AB3)

$\displaystyle \varrho(r)=r^{3} - r^{2}$

$\displaystyle \sigma(r)=\frac{23 r^{2}}{12} - \frac{4 r}{3} + \frac{5}{12}$

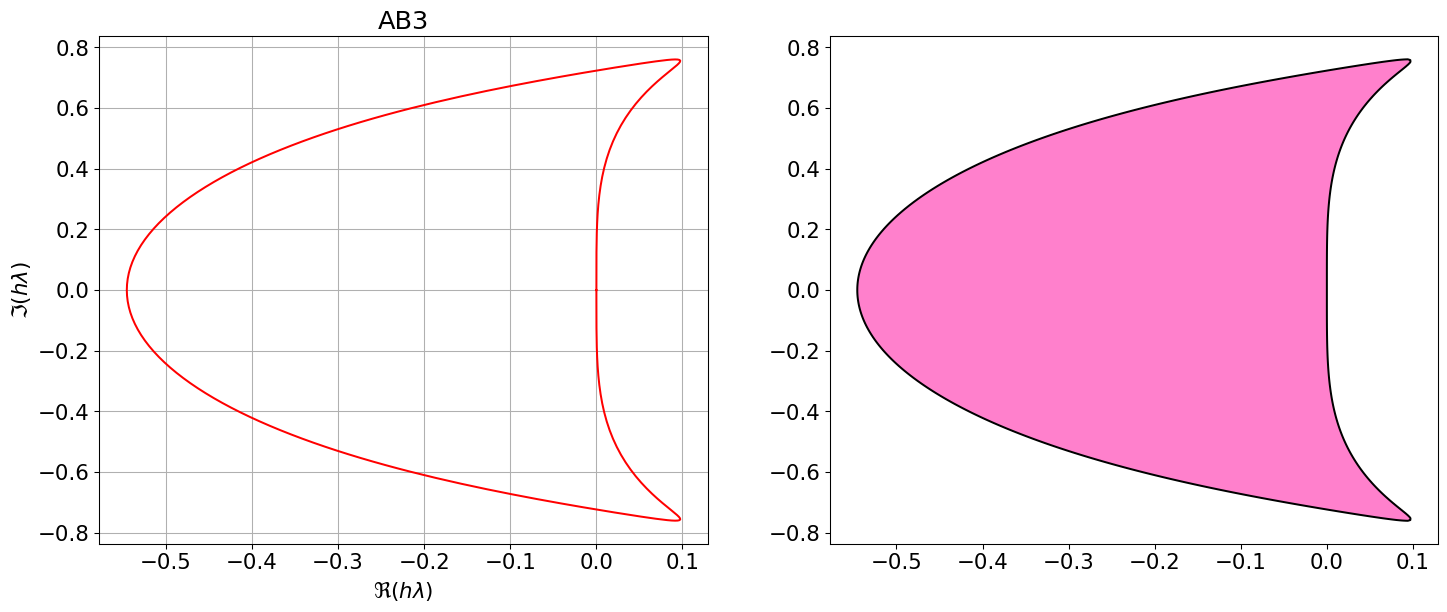
Code

AB4 = { <span class="st">"Nom"</span>:<span class="st">"AB4"</span>, <span class="st">"p"</span>:<span class="dv">3</span>, <span class="st">"aa"</span>:[<span class="dv">1</span>,<span class="dv">0</span>,<span class="dv">0</span>,<span class="dv">0</span>], <span class="st">"bb"</span>:[sp.Rational(<span class="dv">55</span>,<span class="dv">24</span>),<span class="op">-</span>sp.Rational(<span class="dv">59</span>,<span class="dv">24</span>), sp.Rational(<span class="dv">37</span>,<span class="dv">24</span>), <span class="op">-</span>sp.Rational(<span class="dv">9</span>,<span class="dv">24</span>)], <span class="st">"bm1"</span>:<span class="dv">0</span>  }
polyCar(AB4)
Astabilite(AB4)

$\displaystyle \varrho(r)=r^{4} - r^{3}$

$\displaystyle \sigma(r)=\frac{55 r^{3}}{24} - \frac{59 r^{2}}{24} + \frac{37 r}{24} - \frac{3}{8}$

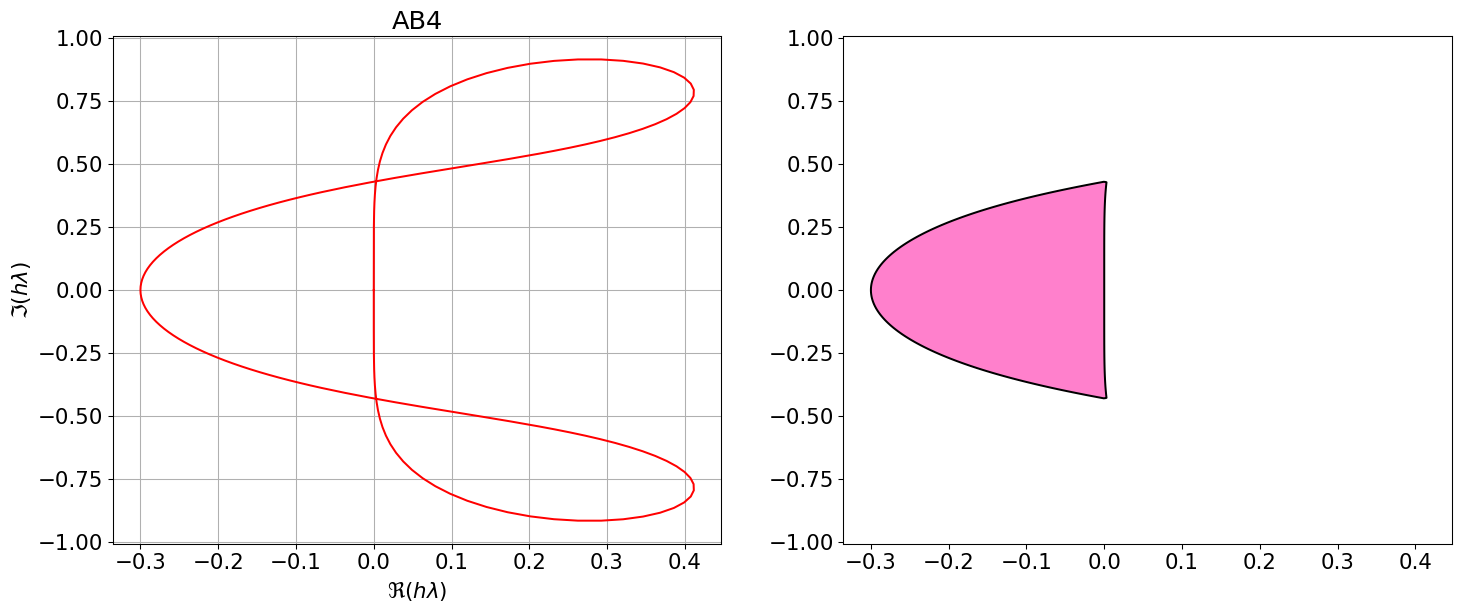
Code

AB5 = { <span class="st">"Nom"</span>:<span class="st">"AB5"</span>, <span class="st">"p"</span>:<span class="dv">4</span>, <span class="st">"aa"</span>:[<span class="dv">1</span>,<span class="dv">0</span>,<span class="dv">0</span>,<span class="dv">0</span>,<span class="dv">0</span>], <span class="st">"bb"</span>:[sp.Rational(<span class="dv">1901</span>,<span class="dv">720</span>), <span class="op">-</span>sp.Rational(<span class="dv">1387</span>,<span class="dv">360</span>), sp.Rational(<span class="dv">109</span>,<span class="dv">30</span>), <span class="op">-</span>sp.Rational(<span class="dv">637</span>,<span class="dv">360</span>), sp.Rational(<span class="dv">251</span>,<span class="dv">720</span>)], <span class="st">"bm1"</span>:<span class="dv">0</span>  }
polyCar(AB5)
Astabilite(AB5)

$\displaystyle \varrho(r)=r^{5} - r^{4}$

$\displaystyle \sigma(r)=\frac{1901 r^{4}}{720} - \frac{1387 r^{3}}{360} + \frac{109 r^{2}}{30} - \frac{637 r}{360} + \frac{251}{720}$

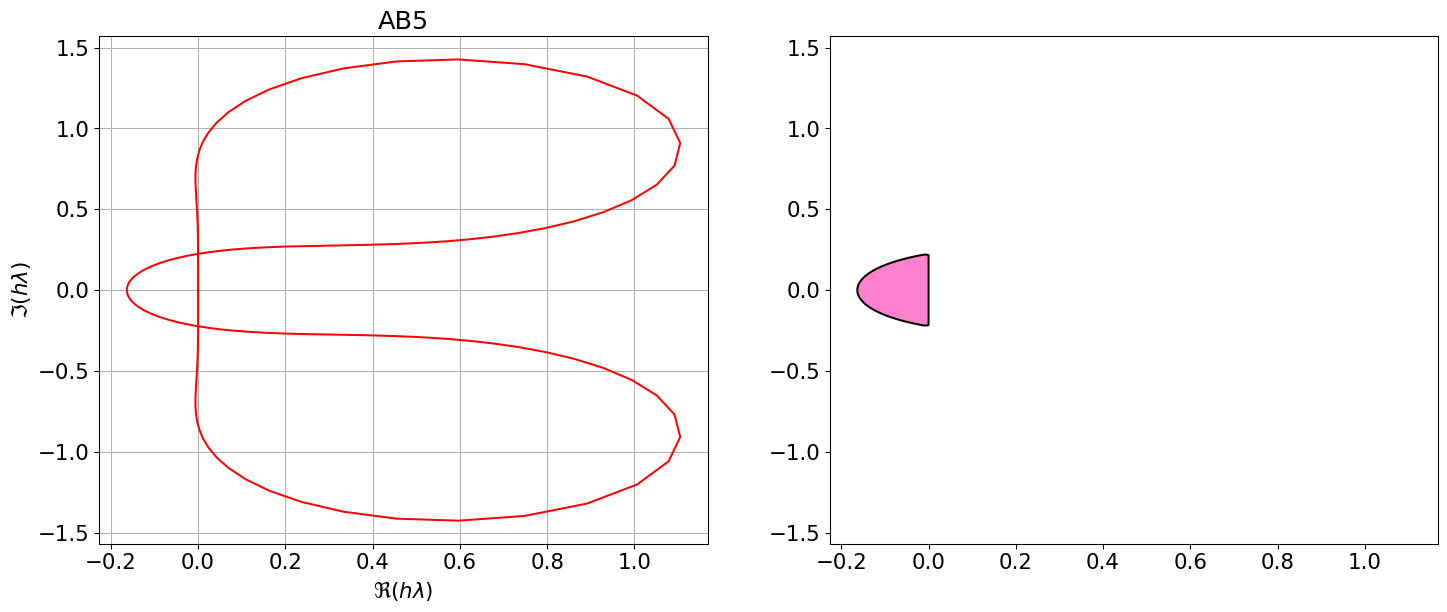
Code

AM0 = { <span class="st">"Nom"</span>:<span class="st">"AM0=EI"</span>, <span class="st">"p"</span>:<span class="dv">0</span>, <span class="st">"aa"</span>:[<span class="dv">1</span>], <span class="st">"bb"</span>:[<span class="dv">0</span>], <span class="st">"bm1"</span>: <span class="dv">1</span>  }
polyCarIMPL(AM0)
#Astabilite(AM0)

$\displaystyle \varrho(r)=r$

$\displaystyle \sigma(r)=r$

Code

AM1 = { <span class="st">"Nom"</span>:<span class="st">"AM1=CN"</span>, <span class="st">"p"</span>:<span class="dv">1</span>, <span class="st">"aa"</span>:[<span class="dv">1</span>], <span class="st">"bb"</span>:[sp.Rational(<span class="dv">1</span>,<span class="dv">2</span>)], <span class="st">"bm1"</span>: sp.Rational(<span class="dv">1</span>,<span class="dv">2</span>)  }
polyCarIMPL(AM1)
#Astabilite(AM1)

$\displaystyle \varrho(r)=r^{2} - r$

$\displaystyle \sigma(r)=\frac{r^{2}}{2} + \frac{r}{2}$

Code

AM2 = { <span class="st">"Nom"</span>:<span class="st">"AM2"</span>, <span class="st">"p"</span>:<span class="dv">1</span>, <span class="st">"aa"</span>:[<span class="dv">1</span>,<span class="dv">0</span>], <span class="st">"bb"</span>:[sp.Rational(<span class="dv">8</span>,<span class="dv">12</span>),<span class="op">-</span>sp.Rational(<span class="dv">1</span>,<span class="dv">12</span>)], <span class="st">"bm1"</span>:sp.Rational(<span class="dv">5</span>,<span class="dv">12</span>) }
polyCar(AM2)
Astabilite(AM2)

$\displaystyle \varrho(r)=r^{2} - r$

$\displaystyle \sigma(r)=\frac{5 r^{2}}{12} + \frac{2 r}{3} - \frac{1}{12}$

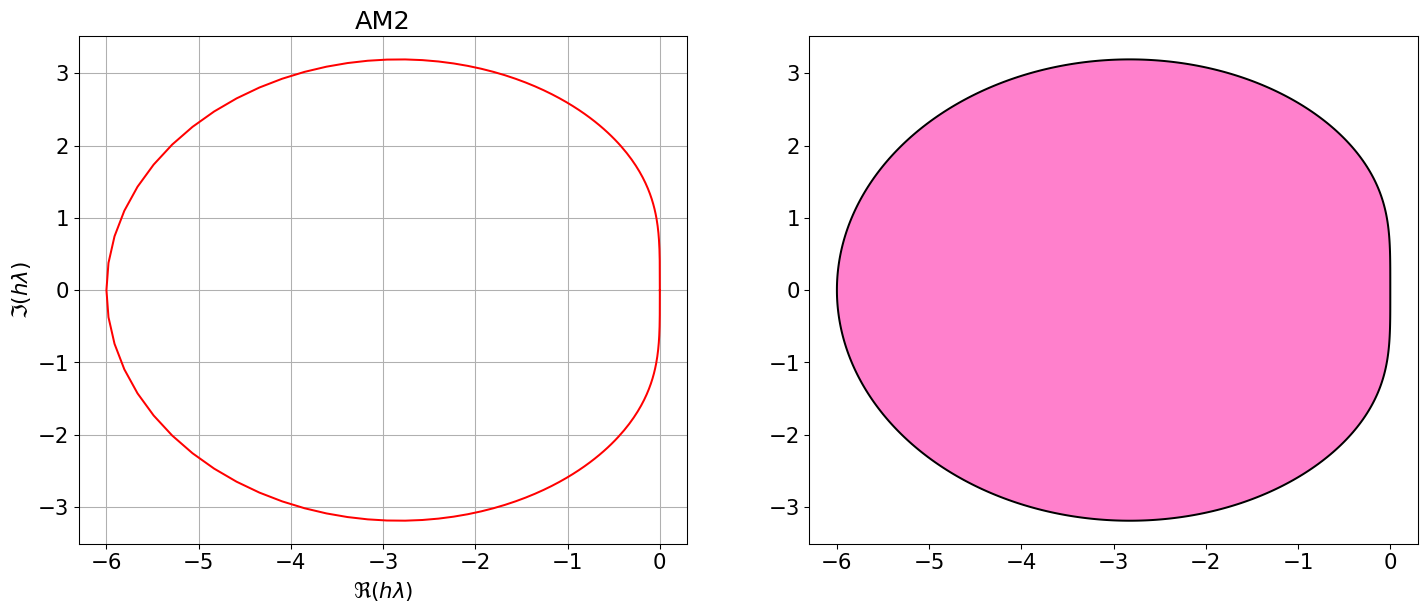
Code

AM3 = { <span class="st">"Nom"</span>:<span class="st">"AM3"</span>, <span class="st">"p"</span>:<span class="dv">2</span>, <span class="st">"aa"</span>:[<span class="dv">1</span>,<span class="dv">0</span>,<span class="dv">0</span>], <span class="st">"bb"</span>:[sp.Rational(<span class="dv">19</span>,<span class="dv">24</span>),<span class="op">-</span>sp.Rational(<span class="dv">5</span>,<span class="dv">24</span>),sp.Rational(<span class="dv">1</span>,<span class="dv">24</span>)], <span class="st">"bm1"</span>:sp.Rational(<span class="dv">9</span>,<span class="dv">24</span>)  }
polyCar(AM3)
Astabilite(AM3)

$\displaystyle \varrho(r)=r^{3} - r^{2}$

$\displaystyle \sigma(r)=\frac{3 r^{3}}{8} + \frac{19 r^{2}}{24} - \frac{5 r}{24} + \frac{1}{24}$

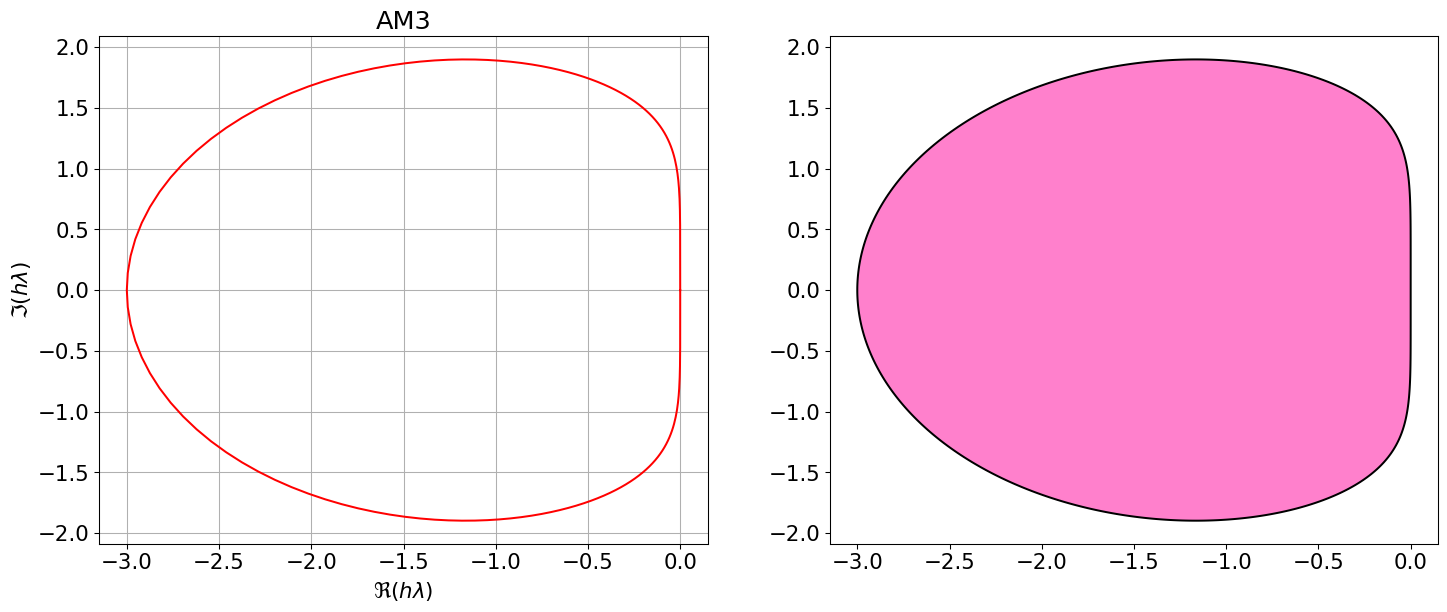
Code

AM4 = { <span class="st">"Nom"</span>:<span class="st">"AM4"</span>, <span class="st">"p"</span>:<span class="dv">3</span>, <span class="st">"aa"</span>:[<span class="dv">1</span>,<span class="dv">0</span>,<span class="dv">0</span>,<span class="dv">0</span>], <span class="st">"bb"</span>:[sp.Rational(<span class="dv">646</span>,<span class="dv">720</span>), sp.Rational(<span class="op">-</span><span class="dv">264</span>,<span class="dv">720</span>), sp.Rational(<span class="dv">106</span>,<span class="dv">720</span>), sp.Rational(<span class="op">-</span><span class="dv">19</span>,<span class="dv">720</span>)], <span class="st">"bm1"</span>:sp.Rational(<span class="dv">251</span>,<span class="dv">720</span>)  }
polyCar(AM4)
Astabilite(AM4)

$\displaystyle \varrho(r)=r^{4} - r^{3}$

$\displaystyle \sigma(r)=\frac{251 r^{4}}{720} + \frac{323 r^{3}}{360} - \frac{11 r^{2}}{30} + \frac{53 r}{360} - \frac{19}{720}$

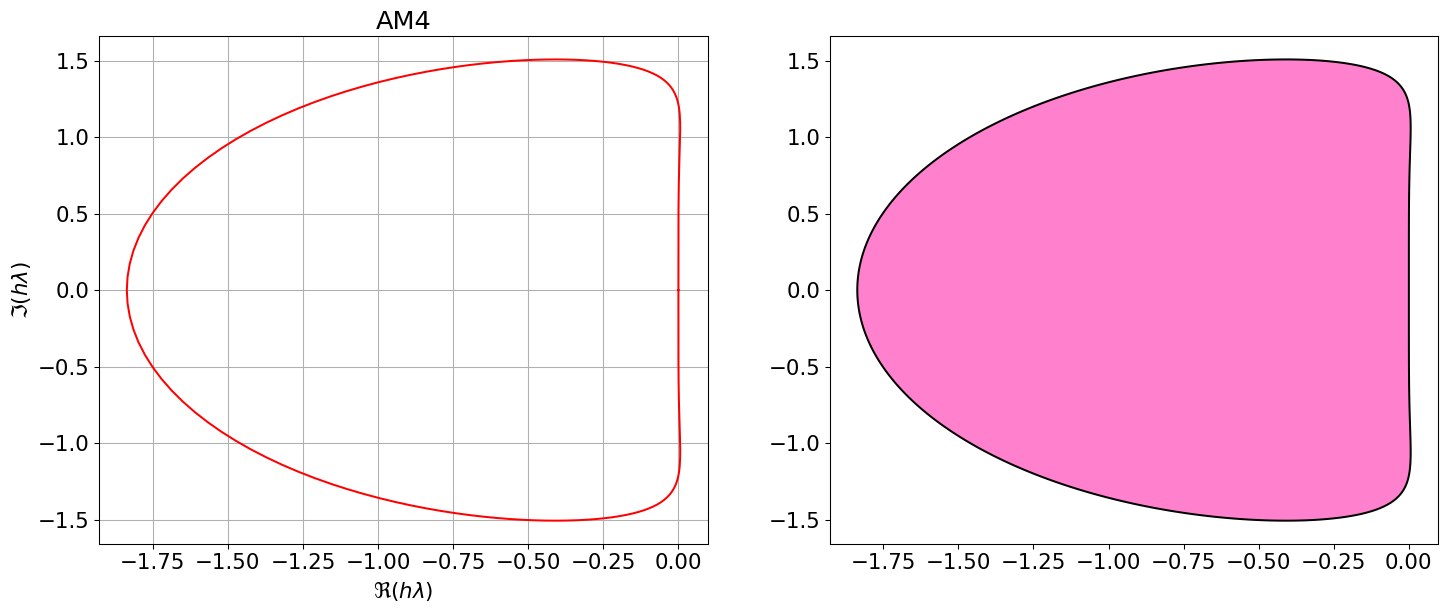
Code

MS2 = { <span class="st">"Nom"</span>:<span class="st">"MS2"</span>, <span class="st">"p"</span>:<span class="dv">1</span>, <span class="st">"aa"</span>:[<span class="dv">0</span>,<span class="dv">1</span>], <span class="st">"bb"</span>:[sp.Rational(<span class="dv">4</span>,<span class="dv">3</span>),sp.Rational(<span class="dv">1</span>,<span class="dv">3</span>)], <span class="st">"bm1"</span>:sp.Rational(<span class="dv">1</span>,<span class="dv">3</span>) }
polyCar(MS2)
#Astabilite(MS2)

$\displaystyle \varrho(r)=r^{2} - 1$

$\displaystyle \sigma(r)=\frac{r^{2}}{3} + \frac{4 r}{3} + \frac{1}{3}$

Code

BDF1 = { <span class="st">"Nom"</span>:<span class="st">"BDF1=EI"</span>, <span class="st">"p"</span>:<span class="dv">1</span>, <span class="st">"aa"</span>:[<span class="dv">1</span>], <span class="st">"bb"</span>:[<span class="dv">0</span>], <span class="st">"bm1"</span>:<span class="dv">1</span>  }
polyCarIMPL(BDF1)
Astabilite(BDF1)

$\displaystyle \varrho(r)=r^{2} - r$

$\displaystyle \sigma(r)=r^{2}$

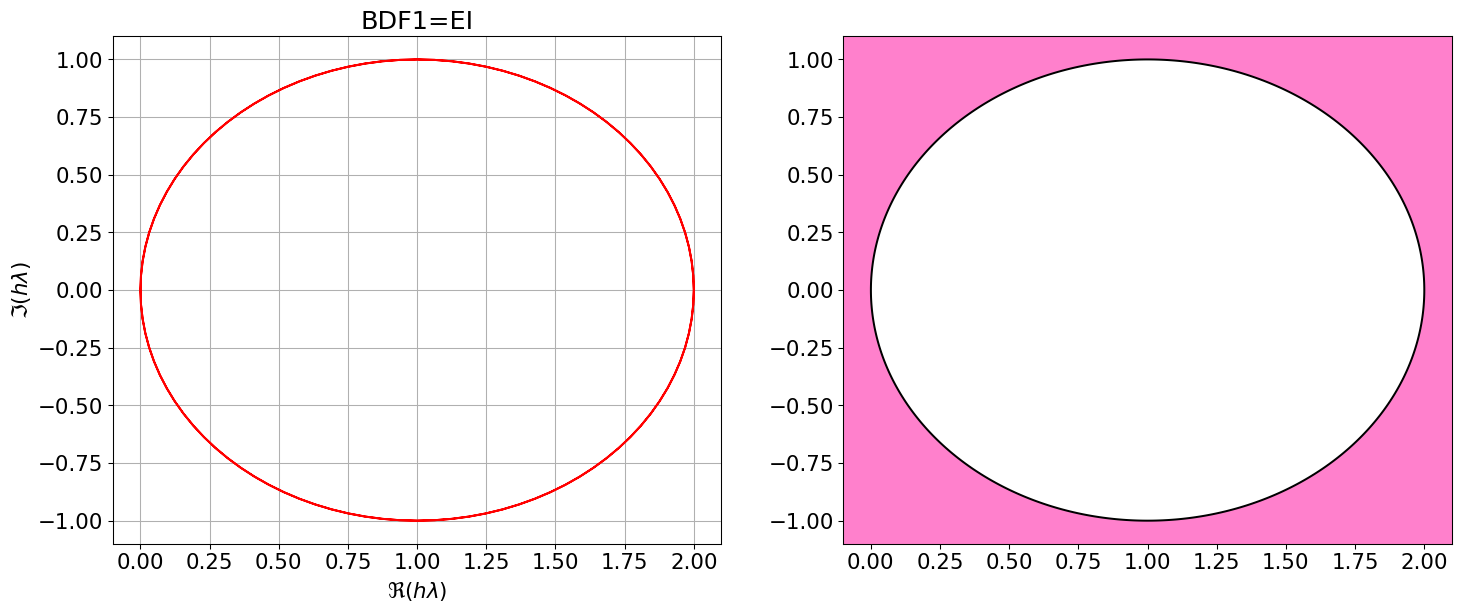
Code

BDF2 = { <span class="st">"Nom"</span>:<span class="st">"BDF2"</span>, <span class="st">"p"</span>:<span class="dv">1</span>, <span class="st">"aa"</span>:[sp.Rational(<span class="dv">4</span>,<span class="dv">3</span>),<span class="op">-</span>sp.Rational(<span class="dv">1</span>,<span class="dv">3</span>)], <span class="st">"bb"</span>:[<span class="dv">0</span>], <span class="st">"bm1"</span>:sp.Rational(<span class="dv">2</span>,<span class="dv">3</span>) }
polyCarIMPL(BDF2)
Astabilite(BDF2)

$\displaystyle \varrho(r)=r^{2} - \frac{4 r}{3}$

$\displaystyle \sigma(r)=\frac{2 r^{2}}{3}$

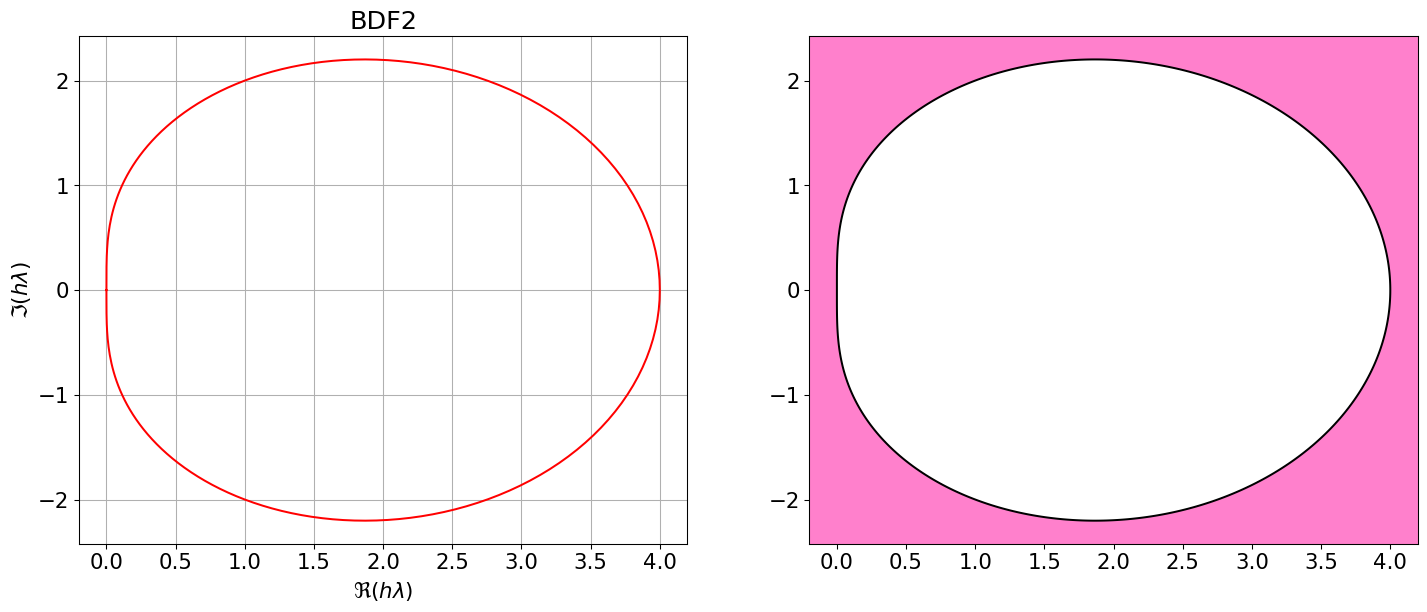
Code

BDF3 = { <span class="st">"Nom"</span>:<span class="st">"BDF3"</span>, <span class="st">"p"</span>:<span class="dv">2</span>, <span class="st">"aa"</span>:[sp.Rational(<span class="dv">18</span>,<span class="dv">11</span>),<span class="op">-</span>sp.Rational(<span class="dv">9</span>,<span class="dv">11</span>),sp.Rational(<span class="dv">2</span>,<span class="dv">11</span>)], <span class="st">"bb"</span>:[<span class="dv">0</span>], <span class="st">"bm1"</span>:sp.Rational(<span class="dv">6</span>,<span class="dv">11</span>)  }
#polyCarIMPL(BDF3)
Astabilite(BDF3)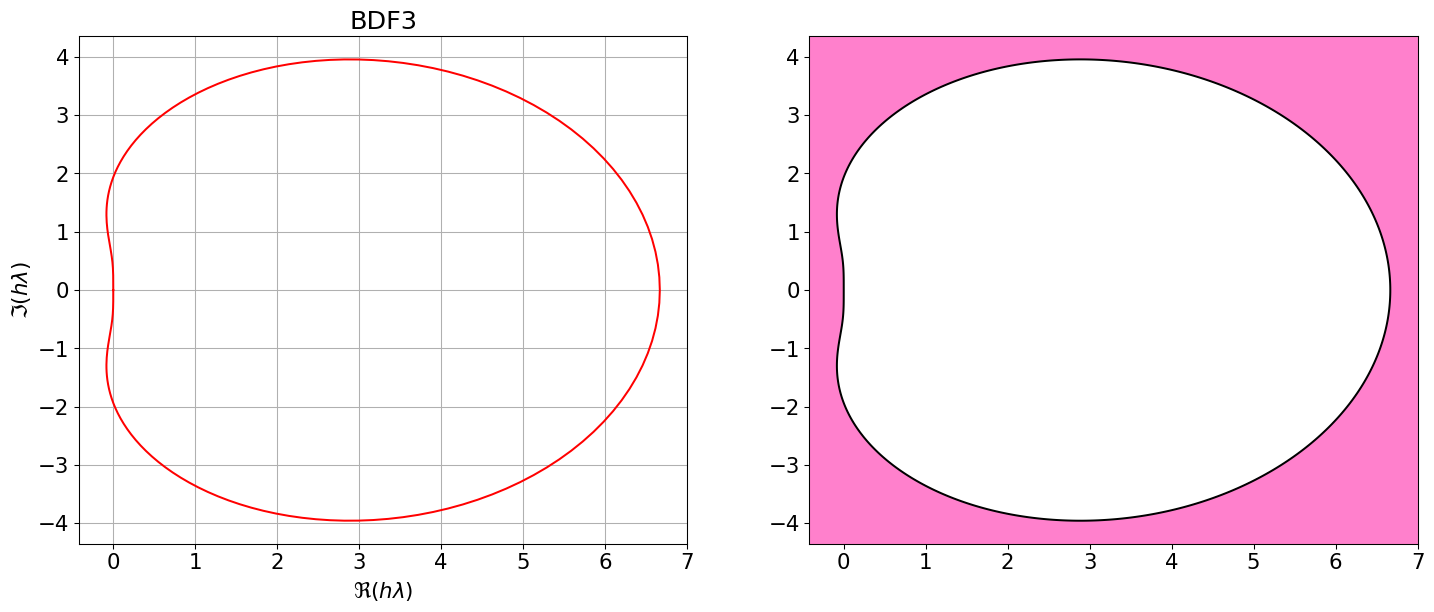

Code

BDF4 = { <span class="st">"Nom"</span>:<span class="st">"BDF4"</span>, <span class="st">"p"</span>:<span class="dv">3</span>, <span class="st">"aa"</span>:[sp.Rational(<span class="dv">48</span>,<span class="dv">25</span>),<span class="op">-</span>sp.Rational(<span class="dv">36</span>,<span class="dv">25</span>),sp.Rational(<span class="dv">16</span>,<span class="dv">25</span>),<span class="op">-</span>sp.Rational(<span class="dv">3</span>,<span class="dv">25</span>)], <span class="st">"bb"</span>:[<span class="dv">0</span>], <span class="st">"bm1"</span>:sp.Rational(<span class="dv">12</span>,<span class="dv">25</span>)  }
# polyCarIMPL(BDF4)
Astabilite(BDF4)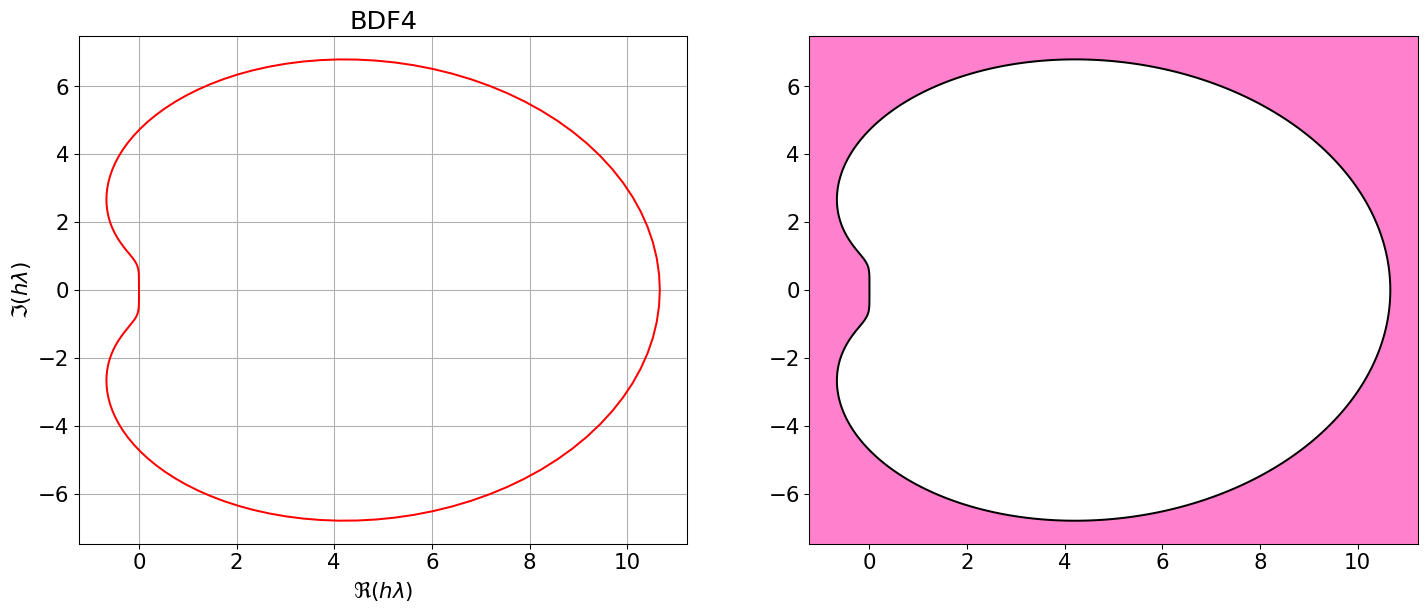

Code

BDF5 = { <span class="st">"Nom"</span>:<span class="st">"BDF5"</span>, <span class="st">"p"</span>:<span class="dv">4</span>, <span class="st">"aa"</span>:[sp.Rational(<span class="dv">300</span>,<span class="dv">137</span>),<span class="op">-</span>sp.Rational(<span class="dv">300</span>,<span class="dv">137</span>),sp.Rational(<span class="dv">200</span>,<span class="dv">137</span>),<span class="op">-</span>sp.Rational(<span class="dv">75</span>,<span class="dv">137</span>),sp.Rational(<span class="dv">12</span>,<span class="dv">137</span>)], <span class="st">"bb"</span>:[<span class="dv">0</span>], <span class="st">"bm1"</span>:sp.Rational(<span class="dv">60</span>,<span class="dv">137</span>) }
# polyCar(BDF5)
Astabilite(BDF5)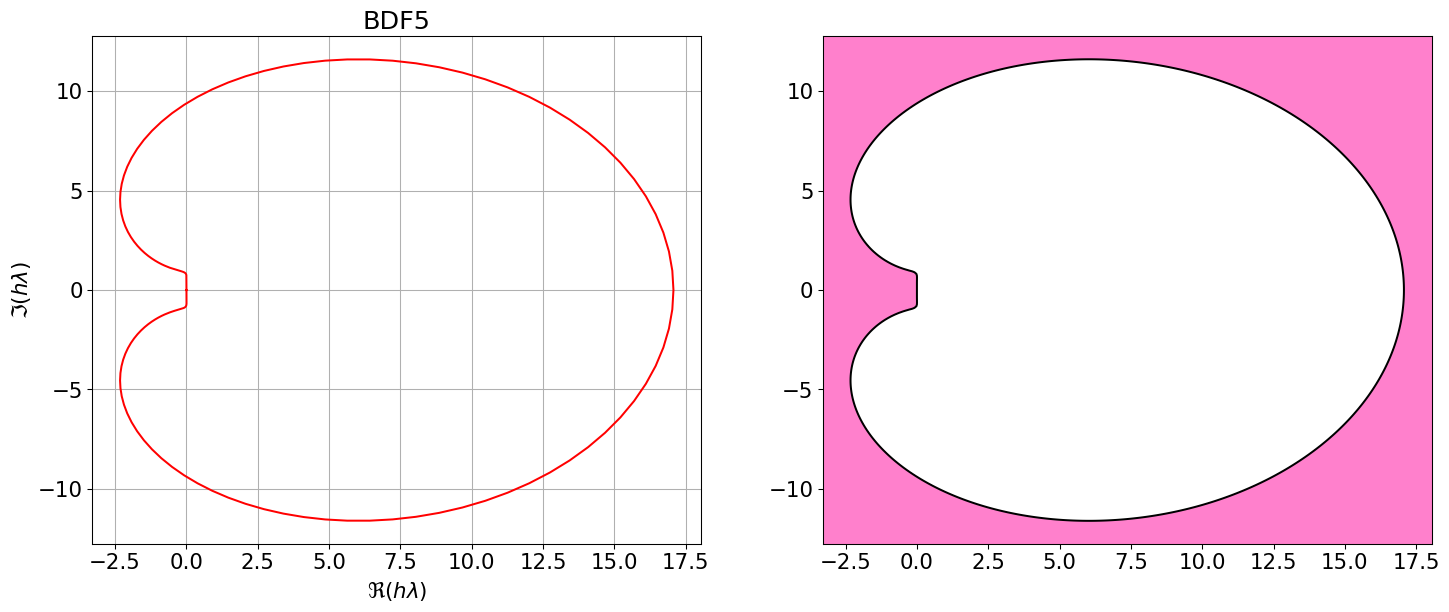

Code

BDF6 = { <span class="st">"Nom"</span>:<span class="st">"BDF6"</span>, <span class="st">"p"</span>:<span class="dv">5</span>, <span class="st">"aa"</span>:[sp.Rational(<span class="dv">120</span>,<span class="dv">49</span>),<span class="op">-</span>sp.Rational(<span class="dv">150</span>,<span class="dv">49</span>),sp.Rational(<span class="dv">400</span>,<span class="dv">147</span>),<span class="op">-</span>sp.Rational(<span class="dv">75</span>,<span class="dv">49</span>),sp.Rational(<span class="dv">24</span>,<span class="dv">49</span>),<span class="op">-</span>sp.Rational(<span class="dv">10</span>,<span class="dv">147</span>)], <span class="st">"bb"</span>:[<span class="dv">0</span>], <span class="st">"bm1"</span>:sp.Rational(<span class="dv">20</span>,<span class="dv">49</span>)  }
# polyCar(BDF6)
Astabilite(BDF6)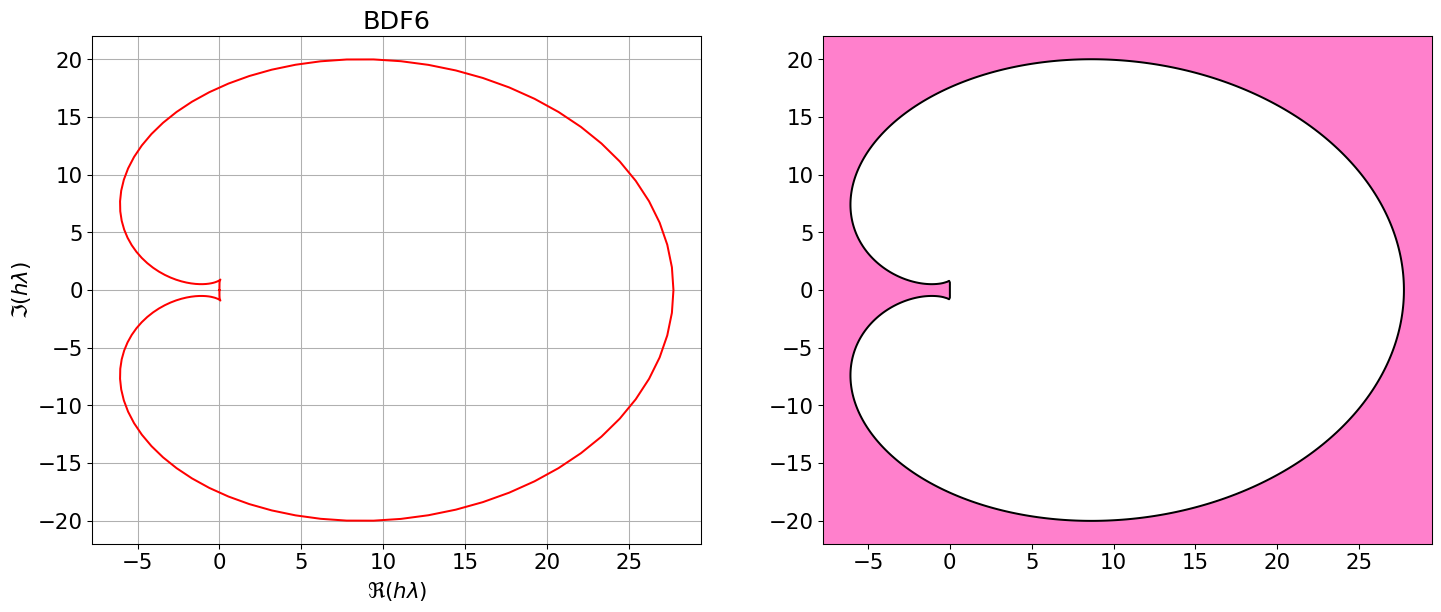

4 Exercice

Pour les méthodes d’Euler explicite, Euler implicite et Cranck-Nicolson :

Trouver les coefficients $p\ge0$, $\{a_k\}$ et $\{b_k\}$ tels que $ u_{n+1} = \sum_{j=0}^p a_ju_{n-j}+h\sum_{j=0}^p b_j\varphi(t_{n-j},u_{n-j})+hb_{-1}\varphi(t_{n+1},u_{n+1}), \qquad n=p,p+1,\dots,N-1$

Écrire le premier polynôme caractéristique $\varrho(r)=r^{p+1}-\sum_{j=0}^p a_jr^{p-j}$ et en calculer les $p+1$ racines $\{r_j\}_{j=0}^p$.

Montrer que la méthode est zéro-stable, i.e. que $\begin{cases} |r_j|\le1 \quad\text{pour tout }j=0,\dots,p \\ \varrho'(r_j)\neq0 \text{ si } |r_j|=1. \end{cases} $

Montrer que la méthode est consistante, i.e. $\xi(0)=\xi(1)=1$.

Étudier l’ordre de consistance, autrement dit trouver le plus grand $\omega\ge1$ tel que $\xi(0)=\xi(1)=\dots=\xi(\omega)=1$.

Étudier la A-stabilité

4.1 Correction

Il s’agit de trois méthodes à $q=1$ pas, donc $p=0$. Voici les $\xi(i)$ correspondants :

Code

xi_cond(p=0, omega=3)

Pour p=0 on a une méthode à q=1 pas, on affiche ξ(i) pour i=0,…,3

$\xi(0) = a_{0}$

$\xi(1) = b_{0} + b_{-1}$

$\xi(2) = 2 b_{-1}$

$\xi(3) = 3 b_{-1}$

4.2 Euler explicite

$u_{n+1}=u_n+h\varphi(t_n,u_n)$ donc $p=0$, $q=1$, $a_0=1$, $b_{-1}=0$, $b_0=1$
$\varrho(r)=r-1$ donc il n’y a qu’une racine: $r_0=1$
$|r_0|=1$ et $\varrho'(1)=1$ $\leadsto$ le schéma est zéro-stable
$\xi(0)=a_0=1$ et $\xi(1)=b_{-1}+b_0=1$ $\leadsto$ le schéma est consistant
La première barrière nous dit que $\omega\le1$ donc le schéma est d’ordre $\omega=1$. En effet, $\xi(2)=2b_{-1}=0\neq1$.
$u_{n}=(1+\lambda h)^n$ donc il faut $|1+z|<1$ avec $z=h\lambda$.

4.3 Euler implicite

$u_{n+1}=u_n+h\varphi(t_{n+1},u_{n+1})$ donc $p=0$, $a_0=1$, $b_{-1}=1$, $b_0=0$
$\varrho(r)=r-1$ donc il n’y a qu’une racine: $r_0=1$
$|r_0|=1$ et $\varrho'(1)=1$ $\leadsto$ le schéma est zéro-stable
$\xi(0)=a_0=1$ et $\xi(1)=b_{-1}+b_0=1$ $\leadsto$ le schéma est consistant
La première barrière nous dit que $\omega\le2$. On a $\xi(2)=2b_{-1}=2\neq1$ donc le schéma est seulement d’ordre $\omega=1$.
$u_{n}=\frac{1}{(1+\lambda h)^n}$ donc il faut $\left|\frac{1}{1+z}\right|<1$ avec $z=h\lambda$, $h>0$ et $\Re(\lambda)<0$.

4.4 Cranck-Nicolson

$u_{n+1}=u_n+h\Big(\frac{1}{2}\varphi(t_{n+1},u_{n+1})+\frac{1}{2}\varphi(t_{n},u_{n})\Big)$ donc $p=0$, $a_0=1$, $b_{-1}=\frac{1}{2}$, $b_0=\frac{1}{2}$
$\varrho(r)=r-1$ donc il n’y a qu’une racine: $r_0=1$
$|r_0|=1$ et $\varrho'(1)=1$ $\leadsto$ le schéma est zéro-stable
$\xi(0)=a_0=1$ et $\xi(1)=b_{-1}+b_0=1$ $\leadsto$ le schéma est consistant
La première barrière nous dit que $\omega\le2$. On a $\xi(2)=2b_{-1}=1$ donc le schéma est d’ordre $\omega=2$.
$u_{n}=\left(\frac{2+\lambda h}{2-\lambda h}\right)^n$ donc il faut $\left|\frac{2+z}{2-z}\right|<1$ avec $z=h\lambda$, $h>0$ et $\Re(\lambda)<0$. Ceci est vrai pour tout $h>0$.

Retour au sommet

CM 5 - Convergence et A-stabilité des schémas 👣 multipas 👣 linéaires

1 Polynômes caractéristiques

2 Convergence d’un schéma multipas linéaire

2.1 1️⃣ Consistance

2.2 2️⃣ Zéro-stabilité

2.3 3️⃣ Ordre de convergence

2.4 Méthodes cycliques composites

3 A-stabilité (dans \(\mathbb{C}\))

3.1 Région de A-stabilité (dans \(\mathbb{C}\))

4 Exercice

4.1 Correction

4.2 Euler explicite

4.3 Euler implicite

4.4 Cranck-Nicolson