M62 Étude de schémas numériques pour l’approximation de problèmes de Cauchy - 2021 Contrôle Terminal session 2

2021 Contrôle Terminal session 2

Auteur·rice

Gloria FACCANONI

Date de publication

24 mars 2024

1 Exercice 1 : étude d’un schéma

On étudie le schéma de résolution du problème de Cauchy \(y'(t)=\varphi(t,y(t))\) et \(y(t_0)=y_0\) défini par la formule de récurrence

\( \begin{cases} u_0 = y_0 \\ K_1 = \varphi\left(t_n,u_n\right)\\ K_2 = \varphi\left(t_{n}+\frac{1}{2}h,u_n+\frac{1}{2}hK_1\right)\\ K_3 = \varphi\left(t_{n}+h,u_n+hK_1\right)\\ u_{n+1} = u_n + h\left(aK_1+bK_2+cK_3\right) & n=0,1,\dots N-1 \end{cases} \) où \(a,b,c \in [0;1]\).

  1. Pour quelles valeurs du triplet \((a,b,c)\) retrouve-t-on

    • la méthode d’Euler explicite (EE) ?
    • la méthode d’Euler modifiée (EM) ?
    • la méthode de Heun (H) ?

  2. Le schéma peut être vu comme une méthode de type Runge-Kutta. Écrire la matrice de Butcher associée.
    Le schéma est explicite, semi-implicite ou implicite ?

  3. Sans faire de calculs, indiquer quel est l’ordre maximale du schéma.

  4. Étudier théoriquement l’ordre du schéma en fonction de \(a,b,c\).

  5. Étudier théoriquement la A-stabilité du schéma pour les valeurs du triplet \((a,b,c)\) qui donnent l’ordre maximal.

  6. Pour la question 6 on va fixer \((a,b,c)\). Pour cela, écrivez votre nom et prénom dans la cellule ci-dessous et vous obtiendrez un choix pour les paramètres. Implémenter le schéma avec les valeurs \(a,b,c\) trouvées avec vos nom et prénom et approcher la solution du problème de Cauchy suivant avec \(N+1\) points (quelles valers de \(N\) peut-on choisir? justifier la réponse) Vérifier ensuite empiriquement l’ordre de convergence. \( \begin{cases} y'(t)=-50y(t), &t\in[0;1]\\ y(0)=1 \end{cases} \)

Code 
%reset -f
%matplotlib inline

import numpy as np
import matplotlib.pyplot as plt
from scipy.optimize import fsolve

import sympy 
sympy.init_printing()

from IPython.display import display, Math, Markdown
prlat= lambda *args: display(Math(''.join( sympy.latex(arg) for arg in args )))

Q1 [3 points]
Pour quelles valeurs du triplet \((a,b,c)\) retrouve-t-on

  • la méthode d’Euler explicite (EE) ?
  • la méthode d’Euler modifiée (EM) ?
  • la méthode de Heun (H) ?
  • Si \((a,b,c)=(1,0,0)\) on retrouve la méthode d’Euler explicite (EE): \( u_{n+1} = u_n + h K_1 = u_n + h \varphi\left(t_n,u_n\right) \)
  • Si \((a,b,c)=(0,1,0)\) on retrouve la méthode d’Euler modifiée (EM): \( u_{n+1} = u_n + h K_2 = u_n + h \varphi\left(t_{n}+\frac{1}{2}h,u_n+\frac{1}{2}h\varphi\left(t_n,u_n\right)\right) \)
  • Si \((a,b,c)=(\frac{1}{2},0,\frac{1}{2})\) on retrouve la méthode de Heun (H): \( u_{n+1} = u_n + \frac{h}{2} (K_1+K_3) = u_n + \frac{h}{2} \left(\varphi\left(t_n,u_n\right)+\varphi\left(t_{n}+h,u_n+h\varphi\left(t_n,u_n\right)\right)\right) \)

Q2 [2 points]
Le schéma peut être vu comme une méthode de type Runge-Kutta. Écrire la matrice de Butcher associée.
Le schéma est explicite, semi-implicite ou implicite ?

\( \begin{array}{c|ccc} 0 & 0 & 0 & 0 \\ \dfrac{1}{2} & \dfrac{1}{2} & 0 & 0 \\ 1 & 1 & 0 & 0 \\ \hline & a & b & c \end{array} \) Le schéma est explicite (la matrice \(\mathbb{A}\) est triangulaire inférieure à diagonale nulle).

Q3 [1 points]
Sans faire de calculs, indiquer quel est l’ordre maximale du schéma.

Soit \(\omega\) l’ordre de la méthode et \(s=3\) le nombre d’étages. Étant un schéma explicite, \(\omega\le s=3\).

Q4 [3 points]
Étudier théoriquement l’ordre du schéma en fonction de \(a,b,c\).

  • Si \(\begin{cases} \displaystyle\sum_{j=1}^s b_{i}=1& \\ \displaystyle c_i=\sum_{j=1}^s a_{ij}&i=1,\dots,s \end{cases}\) alors \(\omega\ge1\)

  • Si \(\omega\ge1\) et \(\displaystyle\sum_{j=1}^s b_j c_j=\frac{1}{2}\) alors \(\omega\ge2\)

  • Si \(\omega\ge2\) et \(\begin{cases}\displaystyle\sum_{j=1}^s b_j c_j^2=\frac{1}{3}\\\displaystyle\sum_{i=1}^s\sum_{j=1}^s b_i a_{ij} c_j=\frac{1}{6}\end{cases}\) alors \(\omega\ge3\)

Il est donc

  • au moins d’ordre 1 ssi \(a=1-b-c\)
  • il est d’ordre 2 ssi, de plus, \(\frac{b}{2}+c=\frac{1}{2}\) donc ssi \(\begin{cases}a=c\\b=1-2c\end{cases}\)
  • il ne peut pas être d’ordre 3 car la deuxième condition n’est jamais satisfaite.

On peut vérifier nos calculs comme ci-dessous:

Code 
def ordre_RK(s, A=None, b=None, c=None):

    j = sympy.symbols('j')
    
    if A is None:
        A = sympy.MatrixSymbol('a', s, s)
    else:
        A = sympy.Matrix(A)
    if c is None:
        c = sympy.symbols(f'c_0:{</span>s<span class="sc">}')    
    if b is None:
        b = sympy.symbols(f'b_0:{</span>s<span class="sc">}')
    
    
    display(Markdown("**Matrice de Butcher**"))
    But = matrice_Butcher(s, A, b, c)
    
    Eqs = []

    display(Markdown(f"**On a {</span>s<span class="op">+</span><span class="dv">1</span><span class="sc">} conditions pour avoir consistance = pour être d'ordre 1**"))
    Eq_1 = ordre_1(s, A, b, c, j)
    Eqs.append(Eq_1)
    
    display(Markdown("**On doit ajouter 1 condition pour être d'ordre 2**"))
    Eq_2 = ordre_2(s, A, b, c, j)
    Eqs.append(Eq_2)

    display(Markdown("**On doit ajouter 2 conditions pour être d'ordre 3**"))
    Eq_3 = ordre_3(s, A, b, c, j)  
    Eqs.extend(Eq_3)  

    return Eqs


def matrice_Butcher(s, A, b, c):
    But = sympy.Matrix(A)
    But = But.col_insert(0, sympy.Matrix(c))   
    last = [sympy.Symbol(" ")]
    last.extend(b)
    But = But.row_insert(s,sympy.Matrix(last).T)
    display(Math(sympy.latex(sympy.Matrix(But))))
    return But


def ordre_1(s, A, b, c, j):
    texte = "\sum_{j=1}^s b_j =" + f"{</span><span class="bu">sum</span>(b)<span class="sc">.</span>simplify()<span class="sc">}"
    texte += r"\text{ doit être égale à }1"
    display(Math(texte))
    Eq_1 = sympy.Eq( sum(b).simplify(), 1 ) 
    for i in range(s):
        somma = sympy.summation(A[i,j],(j,0,s-1)).simplify()
        texte = r'\sum_{j=1}^s a_{'</span><span class="op">+</span><span class="bu">str</span>(i)<span class="op">+</span><span class="vs">r'j}=' + sympy.latex( somma )
        texte += r"\text{ doit être égale à }"+sympy.latex(c[i])
        display(Math( texte ))
        Eq_1 = Eq_1 & sympy.Eq( somma, c[i] )
    return Eq_1    


def ordre_2(s, A, b, c, j):
    texte = '\sum_{j=1}^s b_j c_j=' +sympy.latex(sum([b[i]*c[i] for i in range(s)]).simplify())
    texte += r"\text{ doit être égale à }\frac{1}{2}"
    display(Math(texte))
    Eq_2 = sympy.Eq( sum([b[i]*c[i] for i in range(s)]).simplify(), sympy.Rational(1,2) )
    return Eq_2


def ordre_3(s, A, b, c, j):
    texte = '\sum_{j=1}^s b_j c_j^2='
    texte += sympy.latex( sum([b[i]*c[i]**2 for i in range(s)]).simplify() )
    texte += r"\text{ doit être égale à }\frac{1}{3}"
    display(Math(texte))
    Eq_3_1 = sympy.Eq( sum([b[i]*c[i]**2 for i in range(s)]).simplify(), sympy.Rational(1,3) )
    texte = r'\sum_{i,j=1}^s b_i a_{ij} c_j='    
    somma = sum([b[i]*A[i,j]*c[j] for j in range(s) for i in range(s)]).simplify()
    texte = texte + sympy.latex(somma)
    texte += r"\text{ doit être égale à }\frac{1}{6}"
    display(Math(texte))
    Eq_3_2 = sympy.Eq( sum([b[i]*A[i,j]*c[j] for j in range(s) for i in range(s)]).simplify(), sympy.Rational(1,6) )
    return [Eq_3_1, Eq_3_2]


##################################################
# Conditions avec s étages
##################################################

a,b,c = sympy.symbols('a, b, c')

cc = [0, sympy.Rational(1,2), 1]
bb = [a, b, c]
A = [ [cc[0], 0, 0],
      [cc[1], 0, 0],
      [cc[2], 0, 0]]
s = len(cc)

Eqs = ordre_RK(s, A, bb, cc)

display(Markdown("**Solution pour être d'ordre 2 :**"))
sol = sympy.solve(Eqs[:3])
sol

Matrice de Butcher

\(\displaystyle \left[\begin{matrix}0 & 0 & 0 & 0\\\frac{1}{2} & \frac{1}{2} & 0 & 0\\1 & 1 & 0 & 0\\ & a & b & c\end{matrix}\right]\)

On a 4 conditions pour avoir consistance = pour être d’ordre 1

\(\displaystyle \sum_{j=1}^s b_j =a + b + c\text{ doit être égale à }1\)

\(\displaystyle \sum_{j=1}^s a_{0j}=0\text{ doit être égale à }0\)

\(\displaystyle \sum_{j=1}^s a_{1j}=\frac{1}{2}\text{ doit être égale à }\frac{1}{2}\)

\(\displaystyle \sum_{j=1}^s a_{2j}=1\text{ doit être égale à }1\)

On doit ajouter 1 condition pour être d’ordre 2

\(\displaystyle \sum_{j=1}^s b_j c_j=\frac{b}{2} + c\text{ doit être égale à }\frac{1}{2}\)

On doit ajouter 2 conditions pour être d’ordre 3

\(\displaystyle \sum_{j=1}^s b_j c_j^2=\frac{b}{4} + c\text{ doit être égale à }\frac{1}{3}\)

\(\displaystyle \sum_{i,j=1}^s b_i a_{ij} c_j=0\text{ doit être égale à }\frac{1}{6}\)

Solution pour être d’ordre 2 :

\(\displaystyle \left\{ a : \frac{1}{6}, \ b : \frac{2}{3}, \ c : \frac{1}{6}\right\}\)

Q5 [2 points]
Étudier théoriquement la A-stabilité du schéma pour les valeurs du triplet \((a,b,c)\) qui donnent l’ordre maximal.

Soit \(\beta>0\) un nombre réel positif et considérons le problème de Cauchy \(\begin{cases} y'(t)=-\beta y(t), &\text{pour }t>0,\\ y(0)=1. \end{cases}\) Sa solution est \(y(t)=e^{-\beta t}\) donc \(\lim_{t\to+\infty}|y(t)|=0.\)

Le schéma appliqué à ce problème de Cauchy s’écrit \( \begin{cases} u_0 = y_0 \\ K_1 = -\beta u_n\\ K_2 = -\beta \left(u_n+\frac{1}{2}hK_1\right)=-\beta \left(u_n-\frac{1}{2}\beta h u_n\right)\\ K_3 = -\beta \left(u_n+hK_1\right)=-\beta \left(u_n-\beta h u_n\right)\\ u_{n+1} = u_n + h\left(aK_1+bK_2+cK_3\right) & n=0,1,\dots N-1 \end{cases} \) d’où \( u_{n+1} = \left( 1-(a+b+c)\beta h + \left(\frac{b}{2}+c\right)(\beta h)^2 \right)u_n \)

L’ordre maximal (i.e. l’ordre 2) est obtenu pour \(a+b+c=1\) et \(b=1-2c\), on trouve alors \(u_{n+1} = \left(\dfrac{1}{2}(\beta h)^2 -(\beta h)+1\right)u_n\) Vérifions ces calculs:

Code 
u_n = sympy.Symbol('u_n')
beta = sympy.Symbol(r'\beta', positive=True)
dt = sympy.Symbol('h', positive=True) # pour ne pas effacer l'affectation de "h", ici je vais l'appeler "dt"

K1 = -beta*u_n
display(Math('K_1='+sympy.latex(K1)))
K2 = -beta*(u_n+sympy.Rational(1,2)*dt*K1).factor()
display(Math('K_2='+sympy.latex(K2)))
K3 = -beta*(u_n+dt*K1).factor()
display(Math('K_3='+sympy.latex(K3)))
u_np1 = (u_n+dt*(a*K1+b*K2+c*K3)).factor()
display(Math('u_{n+1}='+sympy.latex(u_np1)))
display(Markdown("Avec les paramètres qui donnent l'ordre 2 on obtient"))
u_np1= u_np1.subs(sol).simplify()
display(Math('u_{n+1}='+sympy.latex(u_np1)))

\(\displaystyle K_1=- \beta u_{n}\)

\(\displaystyle K_2=\frac{\beta u_{n} \left(\beta h - 2\right)}{2}\)

\(\displaystyle K_3=\beta u_{n} \left(\beta h - 1\right)\)

\(\displaystyle u_{n+1}=- \frac{u_{n} \left(- \beta^{2} b h^{2} - 2 \beta^{2} c h^{2} + 2 \beta a h + 2 \beta b h + 2 \beta c h - 2\right)}{2}\)

Avec les paramètres qui donnent l’ordre 2 on obtient

\(\displaystyle u_{n+1}=\frac{u_{n} \left(\beta^{2} h^{2} - 2 \beta h + 2\right)}{2}\)

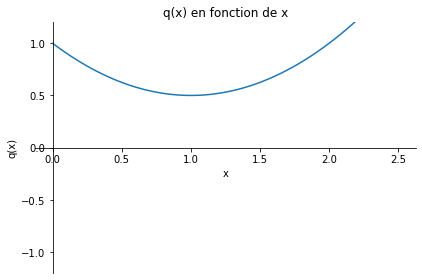
On note \(x=\beta h\) et on étudie la fonction \(q\colon \mathbb{R}^+\to\mathbb{R}\) définie par \(q(x)=\frac{1}{2}x^2-x+1\) car le schéma est A-stable ssi \(|q(x)|<1\).
Il s’agit d’une parabole convexe de sommet en \(x_s=1\) et \(q(x_s)=\frac{1}{2}>-1\) donc \(q(x)<1\) pour \(0<x<2\) et \(q(x)>0\) pour tout \(x\). On conclut que le schéma est A-stable pour tout \(h<\dfrac{2}{\beta}\).

On peut vérifier les calculs avec sympy:

Code 
x = sympy.Symbol('x', positive=True)

q = (u_np1/u_n).simplify().subs(beta*dt,x)
display(Math(sympy.latex(sympy.Eq(sympy.Symbol('q(x)'),q.simplify()))))

display(Markdown("$|q(x)|<1$ ssi"))
display(Math(sympy.latex(sympy.solve(sympy.Abs(q)<1))))

sympy.plot(q, (x,0,2.5), ylim=(-1.2,1.2),
            ylabel='q(x)', xlabel='x', title='q(x) en fonction de x');

\(\displaystyle q(x) = \frac{x^{2}}{2} - x + 1\)

\(|q(x)|<1\) ssi

\(\displaystyle x < 2\)

Pour la question 6 on va fixer \((a,b,c)\). Pour cela, écrivez votre nom et prénom dans la cellule ci-dessous et vous obtiendrez un choix pour les paramètres.

Code 
nom = "Faccanoni"
prenom = "Gloria"

DEN = list(range(3,11))
idx = sum([ord(c) for c in nom+prenom])%len(DEN)
my_c = sympy.Rational(1,DEN[idx])
my_b = 1-2*my_c
display(Math(r'a='+sympy.latex(my_c)+',\\quad b='+sympy.latex(my_c)+',\\quad  c='+sympy.latex(my_b)))


a, b, c = float(my_c), float(my_c), float(my_b)

\(\displaystyle a=\frac{1}{3},\quad b=\frac{1}{3},\quad c=\frac{1}{3}\)

Q6 [2 points]
Implémenter le schéma avec les valeurs \(a,b,c\) trouvées avec vos nom et prénom et approcher la solution du problème de Cauchy suivant avec \(N+1\) points (quelles valers de \(N\) peut-on choisir? justifier la réponse) \( \begin{cases} y'(t)=-50y(t), &t\in[0;1]\\ y(0)=1 \end{cases} \) Vérifier ensuite empiriquement l’ordre de convergence.

Pour la A-stabilité il faut que \(h\) soit \(<\frac{2}{50}\) donc \(N>\frac{1-0}{h}=\frac{50}{2}\)

Code 
# ==================================================
# SCHÉMA RK
# ==================================================

# def RK(tt,phi,y0): # comme suite geometrique
#     h = tt[1]-tt[0]
#     x = beta*h
#     q = x**2/2-x+1
#     uu = y0*q**np.arange(len(tt))
#     return uu

def RK(tt,phi,y0):
    uu = np.empty_like(tt)
    uu[0] = y0
    h = tt[1]-tt[0]
    for n in range(len(tt)-1):
        K1 = phi(tt[n],uu[n])
        K2 = phi(tt[n]+h/2,uu[n]+h/2*K1)
        K3 = phi(tt[n+1],uu[n]+h*K1)
        uu[n+1] = uu[n]+h*(a*K1+b*K2+c*K3)
    return uu


# ==================================================
# EDO
# ==================================================
t0, y0, tfinal = 0, 1, 1
beta = 5

phi = lambda t,y : -beta*y
sol_exacte = lambda t : np.exp(-beta*t)

_, ax = plt.subplots(nrows=1,ncols=2,figsize=(15,5))

# ==================================================
# UN TEST
# ==================================================
N = int(50/2)+10
tt = np.linspace(t0,tfinal,N+1)
h = tt[1]-tt[0]

if h>=2/beta:
    print('Attention: h > limite de stabilité')
    
yy = sol_exacte(tt)
uu = RK(tt,phi,y0)
ax[0].plot(tt,yy,'b-',label=("Exacte"))
ax[0].plot(tt,uu,'ro',label=("RK"))
ax[0].set_title(f'${</span>N<span class="op">=</span><span class="sc">}$, ${</span>h<span class="op">=</span><span class="sc">:g}<{</span><span class="dv">2</span><span class="op">/</span>beta<span class="sc">:g}$')
ax[0].set_xlabel('$t$')
ax[0].set_ylabel('$u$')
ax[0].legend() 
ax[0].grid(True)

# ==================================================
# CONVERGENCE
# ==================================================
H = []
err = []
N = 500
for k in range(7):
    N += 100
    tt = np.linspace(t0, tfinal, N + 1)
    h = tt[1] - tt[0]
    yy = sol_exacte(tt)
    uu = RK(tt,phi,y0)
    H.append(h)
    err.append(np.linalg.norm(yy-uu,np.inf))
    
omega = np.polyfit(np.log(H),np.log(err), 1)[0]
ax[1].plot(np.log(H), np.log(err), 'c-o')
ax[1].set_xlabel('$\ln(h)$')
ax[1].set_ylabel('$\ln(e)$')
ax[1].set_title(rf'Ordre $\omega$={</span>omega<span class="sc">:1.2f}')
ax[1].grid(True);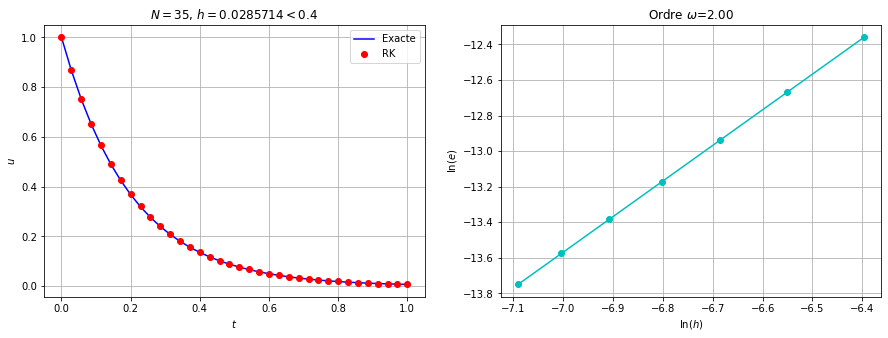

2 Exercice 2 : étude d’un schéma multipas

On notera \(\varphi_k\stackrel{\text{déf}}{=}\varphi(t_k,u_k)\).

Soit la méthode multipas

\( u_{n+1}=u_{n-1} +h\left(b_{-1} \varphi_{n+1} +b_0\varphi_{n}+b_{1} \varphi_{n-1}\right). \)

  1. Pour quelles valeurs des paramètres \(b_0, b_1, b_2\) est-elle zéro-stable ?
  2. Pour quelles valeurs des paramètres la méthode est convergente d’ordre 4 ?
  3. Vérifier empiriquement l’ordre de convergence sur le problème de Cauchy suivant après en avoir calculé la solution exacte : \( \begin{cases} y'(t) = y(t)\ln(1+y(t)), &\forall t \in I=[0,1],\\ y(0) = 2, \end{cases} \)
Code 
%reset -f
%matplotlib inline

import numpy as np
import matplotlib.pyplot as plt
from scipy.optimize import fsolve

import sympy 
sympy.init_printing()

from IPython.display import display, Math, Markdown
prlat= lambda *args: display(Math(''.join( sympy.latex(arg) for arg in args )))

Q1 [2 points]
Pour quelles valeurs des paramètres \(b_0, b_1, b_2\) est-elle zéro-stable?

Le premier polynôme caractéristique est \( \varrho(r)=r^{p+1}-\sum_{j=0}^p a_jr^{p-j}=r^2-a_0r-a_1=r^2-1=(r-1)(r+1) \) dont les racines sont \( r_0=1,\quad r_1=-1. \) La méthode est donc zéro-stable pour tout choix des paramètres car \( \begin{cases} |r_j|\le1 \quad\text{pour tout }j=0,\dots,p \\ \varrho'(r_j)\neq0 \text{ si } |r_j|=1. \end{cases} \)

Q2 [3 points]
Pour quelles valeurs des paramètres la méthode est convergente d’ordre 4?

  • Une méthode consistante d’ordre \(\omega\ge1\) et zéro-stable est convergente d’ordre \(\omega\).
  • On a \(p=1\): c’est une méthode à \(q=p+1=2\) pas avec \(a_0=0\) et \(a_1=1\).
  • La méthode est implicite si \(b_{-1}\neq0\).

La première barrière de Dahlquist affirme qu’un schéma implicite à \(q=2\) étapes consistante et zéro-stable peut être au mieux d’ordre \(\omega=q+2=4\).

Pour que la méthode soit consistante d’ordre 4 il faut que \( \begin{cases} \xi(0)=a_0+a_1=1\\ \xi(1)=b_{0} + b_{1} + b_{-1} - 1 = 1\\ \xi(2)=1 - 2 \left(b_{1} - b_{-1}\right) = 1\\ \xi(3)=3 \left(b_{1} + b_{-1}\right) - 1 = 1\\ \xi(4)=1 - 4 \left(b_{1} - b_{-1}\right) = 1 \end{cases} \) Dans notre cas cela reviens à imposer \( \begin{cases} 0+1=1 \\ {}-1+\big(b_{-1}+b_0+b_1\big)=1 \\ 1-2\big(-b_{-1}+b_1\big)=1 \\ {}-1+3\big(b_{-1}+b_1\big)=1 \\ 1-4\big(-b_{-1}+b_1\big)=1 \end{cases} \) On cherche donc \(b_{-1}\), \(b_0\) et \(b_1\) tels que \( \begin{pmatrix} 1&1&1\\ 2&0&-2\\ 3&0&3\\ 4&0&-4 \end{pmatrix} \begin{pmatrix} b_{-1}\\b_0\\b_1 \end{pmatrix} {}= \begin{pmatrix} 2\\0\\2\\0 \end{pmatrix} \) Il s’agit d’un système surdeterminé qui admet l’unique solution \( b_{-1}=b_1=\frac{1}{3},\qquad b_0=\frac{4}{3} \)

Code 
q = 2  

def xi(i, q):
    sa = sum((-j)**i * aa[j] for j in range(q))
    sb = b_m1 + sum((-j)**(i-1) * bb[j] for j in range(1, q))
    if i == 1:
        sb += bb[0]
    return (sa) + (i * sb).factor()

# Définition des symboles
b_0, b_1  = sympy.symbols('b_0 b_1 ', real=True)
b_m1 = sympy.symbols('b_{-1}', real=True)
aa = [0, 1]
bb = [b_0, b_1]

systeme = [sympy.Eq(xi(i, q),1) for i in range(2*q+1)]
display(Markdown(r"$\begin{cases}"+' '.join([ fr"\xi({</span>i<span class="sc">})="  + sympy.latex(s)+r"\\" for i,s in enumerate(systeme)]) + r"\end{cases}$"))

sol = sympy.solve(systeme)
display(sol)

\(\begin{cases}\xi(0)=\text{True}\\ \xi(1)=b_{0} + b_{1} + b_{-1} - 1 = 1\\ \xi(2)=1 - 2 \left(b_{1} - b_{-1}\right) = 1\\ \xi(3)=3 \left(b_{1} + b_{-1}\right) - 1 = 1\\ \xi(4)=1 - 4 \left(b_{1} - b_{-1}\right) = 1\\\end{cases}\)

\(\displaystyle \left\{ b_{0} : \frac{4}{3}, \ b_{1} : \frac{1}{3}, \ b_{-1} : \frac{1}{3}\right\}\)

Q3 [3 points]
Vérifier empiriquement l’ordre de convergence sur le problème de Cauchy \( \begin{cases} y'(t) = y(t)\ln(1+y(t)), &\forall t \in I=[0,1],\\ y(0) = 2, \end{cases} \) après en avoir calculé la solution exacte.

  • On définit la solution exacte (calculée en utilisant le module sympy) pour estimer les erreurs:
Code 
t0     = 0
tfinal = 1
y0     = 2

phi = lambda t,y : y*np.log(1/y)
Code 
t  = sympy.Symbol('t')
y  = sympy.Function('y')
edo = sympy.Eq( sympy.diff(y(t),t) , y(t)*sympy.log(1/y(t)) )
display(edo)
solpar = sympy.dsolve(edo, y(t), ics={y(t0):y0})
display(solpar)

sol_exacte = sympy.lambdify(t,solpar.rhs,'numpy')

\(\displaystyle \frac{d}{d t} y{\left(t \right)} = y{\left(t \right)} \log{\left(\frac{1}{y{\left(t \right)}} \right)}\)

\(\displaystyle y{\left(t \right)} = e^{e^{- t} \log{\left(2 \right)}}\)

  • On calcule la solution approchée pour différentes valeurs de \(N\):
Code 
def multipas(phi, tt, y0):
    h  = tt[1] - tt[0]
    uu = np.empty_like(tt)
    uu[0] = y0
    uu[:q] = sol_exacte(tt[:q])
    for n in range(q-1,len(tt) - 1):
        temp = fsolve( lambda x : -x+uu[n-1]+h/3*(phi(tt[n+1],x)+4*phi(tt[n],uu[n])+phi(tt[n-1],uu[n-1]))   ,uu[n])
        uu[n+1] = temp[0]
    return uu

H = []
err_mp = []
N = 10
for k in range(7):
    N += 20
    tt = np.linspace(t0, tfinal, N + 1)
    h = tt[1] - tt[0]
    yy = sol_exacte(tt)
    uu_mp = multipas(phi, tt, y0)
    H.append(h)
    err_mp.append(np.linalg.norm(yy-uu_mp,np.inf))

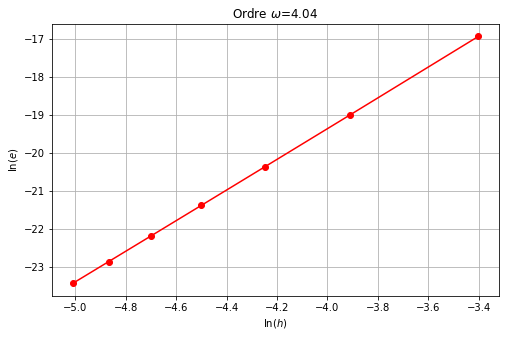
omega = np.polyfit(np.log(H),np.log(err_mp), 1)[0]

plt.figure(figsize=(8,5))
plt.plot(np.log(H), np.log(err_mp), 'r-o')
plt.xlabel('$\ln(h)$')
plt.ylabel('$\ln(e)$')
plt.grid(True)
plt.title(rf'Ordre $\omega$={</span>omega<span class="sc">:1.2f}');

Retour au sommet