TP 2 - Implémentation des schémas “classiques” et étude de la convergence

import sys #only needed to determine Python version number
print('Python version ' + sys.version)

Python version 3.12.3 (main, Jan 17 2025, 18:03:48) [GCC 13.3.0]

Plan de la séance de TP

Cette séance de TP comporte 4 exercices :

• Exercice 1 : Implémentation et test des schémas d’Euler explicite et implicite sur un exemple avec solution exacte. Votre travail consiste à ajouter les autres schémas classiques.

• Exercice 2 : Étude de la convergence empirique des schémas d’Euler explicite et implicite sur le même exemple. Votre travail consiste à ajouter l’étude de la convergence des autres schémas implémentés précédemment.

• Exercice 3 : Application de la méthode d’Euler explicite pour approcher une intégrale elliptique (aucune solution exacte n’est disponible dans ce cas).

• Exercice 4 : Implémentation des schémas classiques appliqués à un système de deux EDO d’ordre 1. Bien que la solution exacte soit disponible pour ce problème, l’accent sera mis sur la conservation d’un invariant, souvent lié à un principe de conservation physique tel que l’énergie totale du système.

1 Exercice (à compléter) : Implémentation des Schémas Classiques

Considérons le problème de Cauchy :

\( \begin{cases} y'(t) = -4y(t)+t^2, &\forall t \in I=[0,1],\\ y(0) = 1. \end{cases}\)

Ci-dessous, nous avons calculé la solution exacte en utilisant le module sympy. Ensuite, nous avons implémenté les schémas d’Euler explicite (EE) et d’Euler implicite (EI).
Nous avons comparé la solution exacte avec les solutions approchées obtenues avec ces deux schémas en utilisant un pas de \(h = \frac{1}{N}\) avec \(N = 8\).
Cette grille grossière permet de bien visualiser les erreurs.

🎯 Travail demandé Ajouter l’implémentation des méthodes suivantes :

• Euler modifié
• RK1_M
• Crank-Nicolson
• Heun

Les endroits où il faut écrire du code sont indiqués par les commentaires commençant par : # !!!!!!

Calculons la solution exacte en utilisant le module sympy:

%reset -f
%matplotlib inline
%autosave 300

import sympy as sym
sym.init_printing()

# Variables
t = sym.Symbol('t')
y = sym.Function('y')

# Equation différentielle
edo = sym.Eq( sym.diff(y(t),t) , -4*y(t)+t**2 )
display(edo)

# Conditions initiales
t0 = 0
y0 = 1
display(sym.Eq(y(t0),y0))

# Méthode directe
solpar = sym.dsolve(edo, y(t), ics={y(t0):y0}) 
display(solpar)

Autosaving every 300 seconds

\(\displaystyle \frac{d}{d t} y{\left(t \right)} = t^{2} - 4 y{\left(t \right)}\)

\(\displaystyle y{\left(0 \right)} = 1\)

\(\displaystyle y{\left(t \right)} = \frac{t^{2}}{4} - \frac{t}{8} + \frac{1}{32} + \frac{31 e^{- 4 t}}{32}\)

On définit la solution exacte à utiliser pour estimer les erreurs:

sol_exacte = sym.lambdify(t,solpar.rhs,'numpy')

On commence par importer les modules numpy et matplotlib et la fonction fsolve du module scipy.optimize pour résoudre l’équation implicite présente dans le schéma implicite :

import matplotlib.pyplot as plt
import numpy as np
plt.rcParams.update({<span class="st">'font.size'</span>: <span class="dv">12</span>}) # plt.rcParams.update(rcParamsDefault)
from scipy.optimize import fsolve # pour les schémas implicites

On initialise le problème de Cauchy

# variables globales
t0     = 0
tfinal = 1
y0     = 1

On définit l’équation différentielle : phi est une lambda function qui contient la fonction mathématique \(\varphi(t, y)=-4y+t^2\) dépendant des variables \(t\) et \(y\).

phi = lambda t,y : -4*y+t**2

On écrit les schémas numériques : les valeurs \([u_0,u_1,\dots,u_{N}]\) pour chaque méthode sont contenues dans le vecteur uu.

Schéma d’Euler explicite :

\( \begin{cases} u_0=y_0,\\ u_{n+1}=u_n+h\varphi(t_n,u_n)& n=0,1,2,\dots N-1 \end{cases} \)

def EE(phi, tt, y0):
    h  = tt[1] - tt[0]
    uu = np.zeros_like(tt)
    uu[0] = y0
    for n in range(len(tt) - 1):
        uu[n+1] = uu[n] + h * phi(tt[n], uu[n])
    return uu

# !!!!!! Ajouter ici le schéma d'Euler modifié : en markdown ET en python

Schéma d’Euler modifié:

\( \begin{cases} u_0=y_0,\\ \tilde u = u_n+\frac{h}{2}\varphi(t_n,u_n),\\ u_{n+1}=u_n+h\varphi\left(t_n+\frac{h}{2},\tilde u\right)& n=0,1,2,\dots N-1 \end{cases} \)

qu’on peut réécrire sous la forme

\( \begin{cases} u_0=y_0,\\ k_1 = \varphi(t_n,u_n),\\ u_{n+1}=u_n+h\varphi\left(t_n+\frac{h}{2}, u_n+h\frac{k_1}{2}\right)& n=0,1,2,\dots N-1 \end{cases} \)

def EM(phi,tt, y0):
    h = tt[1]-tt[0]
    uu = np.zeros_like(tt)
    uu[0] = y0
    for n in range(len(tt)-1):
        k1 = phi( tt[n], uu[n] )
        uu[n+1] = uu[n]+h*phi( tt[n]+h/2 , uu[n]+h*k1/2 ) 
    return uu

# !!!!!! Ajouter ici le schéma de Heun : en markdown ET en python

Schéma de Heun:

\( \begin{cases} u_0=y_0,\\ \tilde u = u_n+h\varphi(t_n,u_n)\\ u_{n+1}=u_n+\frac{h}{2}\Bigl(\varphi(t_n,u_n)+\varphi(t_{n+1},\tilde u)\Bigr)& n=0,1,2,\dots N-1 \end{cases} \)

qu’on peut réécrire sous la forme

\( \begin{cases} u_0=y_0,\\ k_1 = \varphi(t_n,u_n),\\ k_2 = \varphi(t_{n+1},u_n+hk_1),\\ u_{n+1}=u_n+h\frac{k_1+k_2}{2}& n=0,1,2,\dots N-1 \end{cases} \)

def heun(phi,tt, y0):
    h = tt[1]-tt[0]
    uu = np.zeros_like(tt)
    uu[0] = y0
    for n in range(len(tt)-1):
        k1 = phi( tt[n], uu[n] )
        k2 = phi( tt[n+1], uu[n] + h*k1  )
        uu[n+1] = uu[n] + h*(k1+k2)/2 
    return uu

Schéma d’Euler implicite :

\( \begin{cases} u_0=y_0,\\ u_{n+1}=u_n+h\varphi(t_{n+1},u_{n+1})& n=0,1,2,\dots N-1 \end{cases} \)

Attention : \(u_{n+1}\) est solution de l’équation \(x=u_n+h\varphi(t_{n+1},x)\), c’est-à-dire un zéro de la fonction (en générale non linéaire)

\( x\mapsto -x+u_n+h\varphi(t_{n+1},x) \)

def EI(phi, tt, y0):
    h = tt[1] - tt[0]
    uu = np.zeros_like(tt)
    uu[0] = y0
    for n in range(len(tt) - 1):
        temp = fsolve(lambda x: -x + uu[n] + h * phi(tt[n + 1], x), uu[n])
        uu[n+1] = temp[0]
    return uu

# !!!!!! Ajouter ici le schéma de  Crank-Nicolson : en markdown ET en python 

Schéma de Crank-Nicolson :

\( \begin{cases} u_0=y_0,\\ u_{n+1}=u_n+\frac{h}{2}\Bigl(\varphi(t_n,u_n)+\varphi(t_{n+1},u_{n+1})\Bigr)& n=0,1,2,\dots N-1 \end{cases} \)

avec \(u_{n+1}\) zéro de la fonction \(x\mapsto -x+u_n+\frac{h}{2}(\varphi(t_n,u_n)+\varphi(t_{n+1},x))\).

def CN(phi,tt, y0):
    h = tt[1]-tt[0]
    uu = np.zeros_like(tt)
    uu[0] = y0
    for n in range(len(tt)-1):
        temp = fsolve(lambda x: -x+uu[n]+0.5*h*( phi(tt[n+1],x)+phi(tt[n],uu[n]) ), uu[n])
        uu[n+1] = temp[0]
    return uu

# !!!!!! Ajouter ici le schéma RK1_M : en markdown ET en python 

Schéma RK1_M:

\( \begin{cases} u_0=y_0,\\ u_{n+1}=u_n+h\varphi\left(\dfrac{t_n+t_{n+1}}{2},\dfrac{u_n+u_{n+1}}{2}\right)& n=0,1,2,\dots N-1 \end{cases} \)

avec \(u_{n+1}\) zéro de la fonction \(x\mapsto -x+u_n+h\varphi\left(\dfrac{t_n+t_{n+1}}{2},\dfrac{u_n+x}{2}\right)\).

def RK1_M(phi,tt,y0):
    h  = tt[1]-tt[0]
    uu = np.zeros_like(tt)
    uu[0] = y0
    for n in range(len(tt)-1):
        temp = fsolve(lambda x: -x+uu[n]+h*phi( (tt[n]+tt[n+1])/2,(uu[n]+x)/2 ), uu[n])
        uu[n+1] = temp[0]
    return uu

On introduit la discrétisation : les nœuds d’intégration \([t_0,t_1,\dots,t_{N}]\) sont contenus dans le vecteur tt qui contient \(N+1\) points espacés de \(h=\frac{t_N-t_0}{N}\).

On construit la solution exacte discrète et les solutions approchées en ces points :

N = 8 
tt = np.linspace(t0,tfinal,N+1)

# yy      = np.array([sol_exacte(t) for t in tt], dtype=object)
yy      = sol_exacte(tt)  # si vectorisée
uu_ee   = EE(phi, tt, y0)
uu_ei   = EI(phi, tt, y0)
uu_em   = EM(phi, tt, y0)
uu_rk1m = RK1_M(phi, tt, y0)
uu_cn   = CN(phi, tt, y0)
uu_heun = heun(phi, tt, y0)

On compare les graphes de la solution exacte discrète et des solutions approchées et on affiche le maximum de l’erreur :

\( e = \max_{n\in[0,N]} \left| y(t_n)-u_n \right| = ||\mathbf{y}-\mathbf{u}||_{\infty} \)

plt.figure(figsize=(24, 14))

rows, cols, pos = 2, 3, 0

pos +=1 
plt.subplot(rows, cols, pos)
plt.plot(tt, yy, 'b-')
plt.plot(tt, uu_ee, 'r-D')
# err_ee = max( [abs(uu_ee[i] - yy[i]) for n in range(N)] )
err_ee = np.linalg.norm( uu_ee-yy, np.inf)
plt.title(f'Euler explicite\nmax(|erreur|)= {</span>err_ee<span class="sc">:1.10f}')
plt.grid()

pos +=1 
plt.subplot(rows, cols, pos)
plt.plot(tt, yy, 'b-', tt, uu_ei, 'r-D')
# err_ei = max( [abs(uu_ei[i] - yy[i]) for n in range(N)] )
err_ei = np.linalg.norm(uu_ei-yy, np.inf)
plt.title(f'Euler implicite\nmax(|erreur|)={</span>err_ei<span class="sc">:1.2f}')
plt.grid();


pos +=1 
plt.subplot(rows, cols, pos)
plt.plot(tt, yy, 'b-', tt, uu_em, 'r-D')
# err_em = max( [abs(uu_em[i] - yy[i]) for n in range(N)] )
err_em = np.linalg.norm(uu_em-yy, np.inf)
plt.title(f'Euler modifié\nmax(|erreur|)={</span>err_em<span class="sc">:1.5f}')
plt.grid()

pos +=1 
plt.subplot(rows, cols, pos)
plt.plot(tt, yy, 'b-', tt, uu_rk1m, 'r-D')
# err_rk1m = max( [abs(uu_rk1m[i] - yy[i]) for n in range(N)] )
err_rk1m = np.linalg.norm(uu_rk1m-yy, np.inf)
plt.title(f'RK1_m\nmax(|erreur|)={</span>err_rk1m<span class="sc">:1.5f}')
plt.grid()

pos +=1 
plt.subplot(rows, cols, pos)
plt.plot(tt, yy, 'b-', tt, uu_cn, 'r-D')
# err_cn = max( [abs(uu_cn[i] - yy[i]) for n in range(N)] )
err_cn = np.linalg.norm(uu_cn-yy,np.inf)
plt.title(f'Crank Nicolson\nmax(|erreur|)={</span>err_cn<span class="sc">:1.5f}')
plt.grid()

pos +=1 
plt.subplot(rows, cols, pos)
plt.plot(tt, yy, 'b-', tt, uu_heun, 'r-D')
# err_heun = max( [abs(uu_heun[i] - yy[i]) for n in range(N)] )
err_heun = np.linalg.norm(uu_heun-yy, np.inf)
plt.title(f'Heun\nmax(|erreur|)={</span>err_heun<span class="sc">:1.5f}')
plt.grid();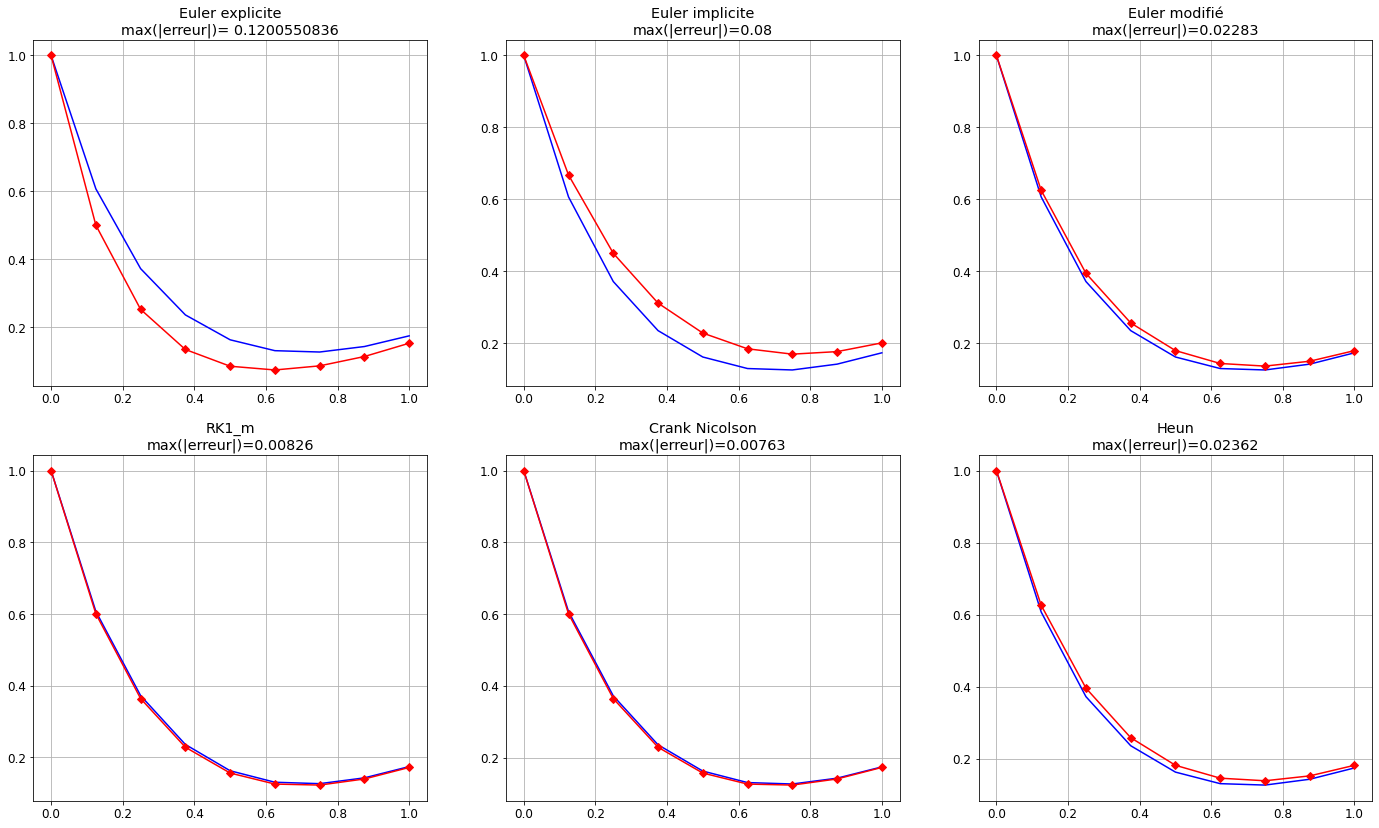

2 Exercice (à compléter) : Estimation de l’Ordre de Convergence

Considérons le même problème de Cauchy.

Ci-dessous, nous avons déjà implémenté et étudié la convergence des méthodes d’Euler explicite (EE) et d’Euler implicite (EI).

• Nous avons calculé la solution approchée pour différentes valeurs de \(h_k = \frac{1}{N_k}\).
• Pour chaque valeur de \(h_k\), nous avons déterminé l’erreur maximale et l’avons sauvegardée dans des vecteurs err_ee (pour EE) et err_ei (pour EI).
• Nous avons ensuite affiché les points \((h[k], \text{err}[k])\) en échelle logarithmique et estimé l’ordre de convergence à l’aide de la fonction polyfit pour chaque méthode.

🎯 Travail demandé Ajouter l’étude de convergence des méthodes suivantes :

• Euler modifié
• RK1_M
• Crank-Nicolson
• Heun

Les endroits où il faut écrire du code sont indiqués par les commentaires commençant par : # !!!!!!

Pour chaque schéma, on calcule la solution approchée avec différentes valeurs de \(h_k=1/N_k\) et on sauvegarde les valeurs de \(h_k\) dans le vecteur H.

Pour chaque valeur de \(h_k\), on calcule le maximum de la valeur absolue de l’erreur et on sauvegarde toutes ces erreurs dans le vecteur err_schema de sort que err_schema[k] contient \(e_k=\max_{i=0,\dots,N_k}|y(t_i)-u_{i}|\).

H = []
err_ee = []
err_ei = []
# !!!!!! Ajouter ici les initialisations des nouveaux schémas
err_em = []
err_rk1m = []
err_cn = []
err_heun = []

for k in range(7):

    N = 2**(k + 3)
    
    tt = np.linspace(t0, tfinal, N + 1)
    h = tt[1] - tt[0]
    yy = sol_exacte(tt)  # si vectorisée
    
    uu_ee   = EE(phi, tt, y0)
    uu_ei   = EI(phi, tt, y0)
    # !!!!!! Ajouter ici l'appel aux nouveaux schémas
    uu_em   = EM(phi, tt, y0)
    uu_rk1m = RK1_M(phi, tt, y0)
    uu_cn   = CN(phi, tt, y0)
    uu_heun = heun(phi, tt, y0)
    
    H.append(h)
    
    err_ee.append(np.linalg.norm(uu_ee-yy,np.inf))
    err_ei.append(np.linalg.norm(uu_ei-yy,np.inf))
    # !!!!!! Ajouter ici le calcul des erreurs
    err_em.append(np.linalg.norm(uu_em-yy,np.inf))
    err_rk1m.append(np.linalg.norm(uu_rk1m-yy,np.inf))
    err_cn.append(np.linalg.norm(uu_cn-yy,np.inf))
    err_heun.append(np.linalg.norm(uu_heun-yy,np.inf))

Pour afficher l’ordre de convergence on utilise une échelle logarithmique, i.e. on représente \(\ln(h)\) sur l’axe des abscisses et \(\ln(\text{err})\) sur l’axe des ordonnées.
En effet, si \(\text{err}=Ch^p\) alors \(\ln(\text{err})=\ln(C)+p\ln(h)\).
En échelle logarithmique, \(p\) représente donc la pente de la ligne droite \(\ln(\text{err})\).

plt.figure(figsize=(10,7))
# plt.plot(np.log(H), np.log(err_ee), 'r-o', label='Euler Explicite')
# plt.plot(np.log(H), np.log(err_ei), 'g-+', label='Euler Implicite')
plt.loglog(H, err_ee, 'r-o', label='Euler Explicite')
plt.loglog(H, err_ei, 'g-+', label='Euler Implicite')
# !!!!!! Ajouter ici les graphes des nouveaux schémas
plt.loglog(H, err_em,   'm-x', label='Euler Modife')
plt.loglog(H, err_rk1m, 'b-^', label='RK1_m')
plt.loglog(H, err_cn,   'y-d', label='Crank Nicolson')
plt.loglog(H, err_heun, 'c-v', label='Heun')
plt.xlabel(r'$h$')
plt.ylabel(r'$e$')
plt.legend(bbox_to_anchor=(1.04, 1), loc='upper left')
plt.grid(True)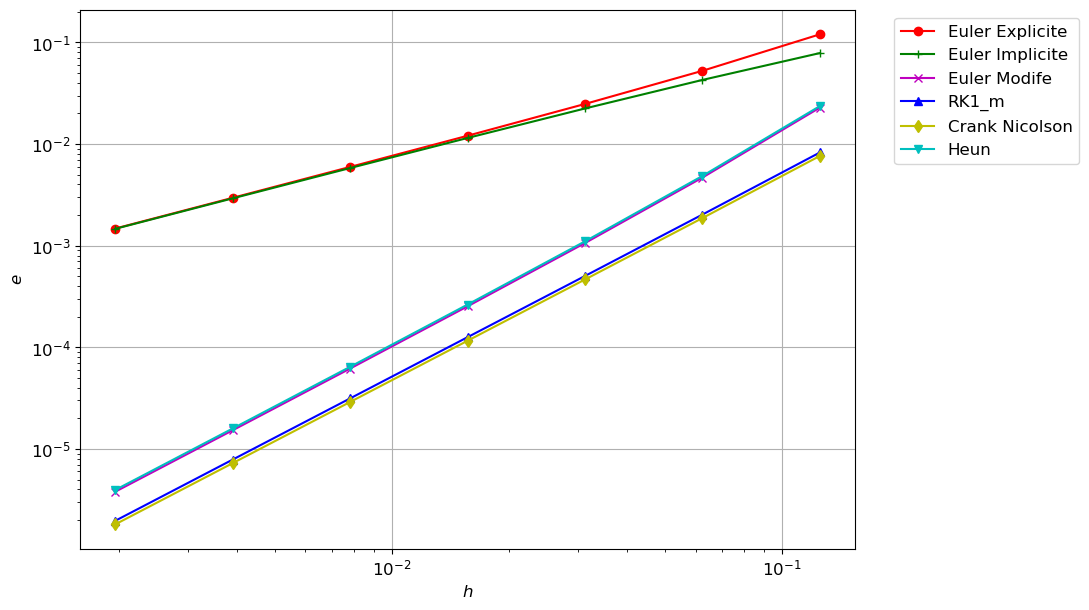

Pour estimer l’ordre de convergence on doit estimer la pente de la droite qui relie l’erreur au pas \(k\) à l’erreur au pas \(k+1\) en echelle logarithmique. Pour estimer la pente globale de cette droite (par des moindres carrés) on peut utiliser la fonction polyfit (du module numpy).

# Calcul des ordres de convergence = pente des droites de regression
# ==================================================================
order_ee = np.polyfit(np.log(H), np.log(err_ee), 1)[0]
order_ei = np.polyfit(np.log(H), np.log(err_ei), 1)[0]
# !!!!!! Ajouter ici les pentes des nouveaux schémas
order_em   = np.polyfit(np.log(H), np.log(err_em), 1)[0]
order_rk1m = np.polyfit(np.log(H), np.log(err_rk1m), 1)[0]
order_cn   = np.polyfit(np.log(H), np.log(err_cn), 1)[0]
order_heun = np.polyfit(np.log(H), np.log(err_heun), 1)[0]


# Print des ordres de convergence
# ===============================

# Version avec print
# print (f'Euler progressif : ordre = {order_ee:1.2f}')
# print (f'Euler regressif  : ordre = {order_ei:1.2f}')
# print (f'Euler modifié  : ordre = {order_em:1.2f}')
# print (f'RK1_M  : ordre = {order_rk1m:1.2f}')
# print (f'Cranck Nicolson  : ordre = {order_cn:1.2f}')
# print (f'Heun  : ordre = {order_heun:1.2f}')

# Version avec tabulate pour une affichage ameliore
from tabulate import tabulate
T = []
T.append( ["Schéma", "Ordre"] )
T.append( ["Euler progressif", order_ee] )
T.append( ["Euler regressif", order_ei] )
T.append( ["Euler modifié", order_em] )
T.append( ["RK1_M", order_rk1m] )
T.append( ["Cranck Nicolson", order_cn] )
T.append( ["Heun", order_heun] )
display(tabulate(T,headers="firstrow",tablefmt="html",floatfmt=".2f"))

Schéma	Ordre
Euler progressif	1.05
Euler regressif	0.96
Euler modifié	2.08
RK1_M	2.00
Cranck Nicolson	2.01
Heun	2.08

3 Exercice : Fonction intégrale

Il existe des fonctions définies par des intégrales qu’on ne peut pas calculer explicitement. Il est pourtant possible de calculer des valeurs approchées de ces fonctions.

Pour \(x\in\left[0;\frac{\pi}{2}\right]\) calculer, afficher la table des valeurs et tracer le graphe de la fonction

\( x \mapsto f(x)=\int_0^x \sqrt{1-\frac{1}{4}\sin^2(t)}\mathrm{d}t \)

en approchant numériquement un problème de Cauchy (lequel?) avec la méthode d’Euler explicite.

Vérifier que \(f\left(\frac{\pi}{6}\right)\simeq0.517881934859938\) et \(f\left(\frac{\pi}{2}\right)\simeq1.46746220933943\).

Remarque : \(f\) est une intégrale elliptique de seconde espèce, cf. https://fr.wikipedia.org/wiki/Int%C3%A9grale_elliptique

Rappel sur la dérivée d’une fonction définie par une intégrale :

\( F(x)=\displaystyle\int_{u(x)}^{v(x)}g(x,t)\mathrm{d}t \qquad\leadsto\qquad F'(x)=\displaystyle g\left(x,v(x)\right)v'(x)-g\left(x,u(x)\right)u'(x)+ \int_{u(x)}^{v(x)} \frac{\partial}{\partial x} g(x,t)\mathrm{d}t. \)

La fonction \(f\) est solution du problème de Cauchy

\( \begin{cases} y'(t)= \sqrt{1-\frac{1}{4}\sin^2(t)},\\ y(0)=0. \end{cases} \)

En effet, \(f(0)=0\) et si on intègre l’EDO entre \(0\) et \(x\) on a

\( f(x)=\int_0^x \sqrt{1-\frac{1}{4}\sin^2(t)}\mathrm{d}t=\int_0^x y'(t)\mathrm{d}t=y(x)-y(0)=y(x). \)

Pour estimer la fonction \(f\) en \(\frac{\pi}{6}\) et \(\frac{\pi}{2}\), nous devons nous assurer que ces valeurs fassent partie des nœuds de discrétisation. Nous avons posé

• \(t_0=0\) le point initial,
• \(t_N=\frac{\pi}{2}\) le point final,
• \(t_i\) les nœuds de discrétisation définis par \(t_i=t_0+ih\) avec le pas de discrétisation \(h=\frac{t_N-t_0}{N}=\frac{\pi}{2N}\).

Nous voulons que \(\frac{\pi}{6}\) soit l’un des nœuds \(t_i\), ce qui revient à chercher un indice \(i\) tel que \(t_i = \frac{\pi}{6}\).

En remplaçant \(t_i\) par sa définition, nous avons \(ih = \frac{\pi}{6}\), soit encore \(i \frac{\pi}{2N} = \frac{\pi}{6}\). On obtient \(i = \frac{2N}{6} = \frac{N}{3}\).

Cela montre que \(\frac{\pi}{6}\) sera un nœud de discrétisation si \(i = \frac{N}{3}\) est un entier. Autrement dit, \(N\) doit être un multiple de \(3\) pour garantir que \(i\) soit entier. Par ailleurs, \(t_N = \frac{\pi}{2}\) est automatiquement inclus comme nœud terminal. Ainsi, pour inclure \(\frac{\pi}{6}\) et \(\frac{\pi}{2}\) parmi les nœuds de discrétisation, il suffit de choisir \(N\) comme un multiple de \(3\).

On calcule enfin la solution approchée et on vérifie que \(f(\pi/6)\simeq0.517881934859938\) et \(f(\pi/2)\simeq1.46746220933943\) et on affiche le graphe de la fonction approchée.

%reset -f
%matplotlib inline

import matplotlib.pyplot as plt
plt.rcParams.update({<span class="st">'font.size'</span>: <span class="dv">12</span>}) # rcParams.update(rcParamsDefault)
import numpy as np


def EE(phi, tt, y0):
    h  = tt[1] - tt[0]
    uu = np.zeros_like(tt)
    uu[0] = y0
    for n in range(len(tt) - 1):
        uu[n+1] = uu[n] + h * phi(tt[n], uu[n])
    return uu

# EDO
phi = lambda t,y : np.sqrt(1-0.25*(np.sin(t))**2)

# CI
t0, y0 = 0, 0

# DISCRETISATION
tfinal = np.pi/2
k = 100
N = 3*k # ainsi t_N=pi/2=3pi/6 et t_k=pi/6
tt = np.linspace(t0,tfinal,N+1)

# CALCUL DE LA SOLUTION APPROCHÉE
uu = EE(phi,tt, y0)

print(f"f(pi/{</span>np<span class="sc">.</span>pi<span class="op">/</span>tt[k]<span class="sc">}) = {</span>uu[k]<span class="sc">:g}") 
print(f"f(pi/{</span>np<span class="sc">.</span>pi<span class="op">/</span>tt[<span class="op">-</span><span class="dv">1</span>]<span class="sc">}) = {</span>uu[<span class="op">-</span><span class="dv">1</span>]<span class="sc">:g}") 

# AFFICHAGE, NON DEMANDÉ
plt.plot(tt,uu)
plt.plot([tt[0],tt[k],tt[k]],[uu[k],uu[k],0],'m--o');
plt.plot([tt[0],tt[-1],tt[-1]],[uu[-1],uu[-1],0],'c--o');

f(pi/6.0) = 0.517965
f(pi/2.0) = 1.46781

Et sympy ? Il dit bien qu’il ne peut pas calculer cette intégrale et qu’il s’agit d’une intégrale elliptique de seconde espèce.

import sympy as sym
sym.init_printing()

t   = sym.Symbol('t')
y   = sym.Function('y')
edo = sym.Eq( sym.diff(y(t),t) , sym.sqrt(1-sym.Rational(1,4)*(sym.sin(t))**2) )
display(edo)
# solgen = sym.dsolve(edo)
# display(solgen)

t  = sym.Symbol('t')
f = sym.Integral(sym.sqrt(1-sym.Rational(1,4)*(sym.sin(t))**2))
display(f)
f.doit()

\(\displaystyle \frac{d}{d t} y{\left(t \right)} = \sqrt{1 - \frac{\sin^{2}{\left(t \right)}}{4}}\)

\(\displaystyle \int \sqrt{1 - \frac{\sin^{2}{\left(t \right)}}{4}}\, dt\)

\(\displaystyle E\left(t\middle| \frac{1}{4}\right)\)

Il est cependant possible d’afficher la valeur “exacte” de l’intégrale elliptique de seconde espèce en utilisant la fonction elliptic_e du module sympy.

display( sym.elliptic_e(np.pi/6,1/4) ) # si on utilise sym.pi, il ne donne pas le résultat float
display( sym.elliptic_e(np.pi/2,1/4) ) 

# help(sym.elliptic_e)

\(\displaystyle 0.517881934859938\)

\(\displaystyle 1.46746220933943\)

4 Exercice : système de Deux EDO avec Invariant

Les résultats numériques doivent être interprétés avec prudence. Les outils numériques ne fournissent que des approximations et n’offrent aucune garantie quant à la validité des résultats obtenus.
Lorsque la solution exacte est inconnue, il faut définir des critères permettant d’évaluer la qualité des approximations. Par exemple, si on connait un invariant théorique, il est souhaitable que l’invariant soit préservé aussi précisément que possible lors d’une simulation numérique.

---

📌 Partie 1 : Problème de Cauchy et invariant

Considérons le problème de Cauchy

\( \begin{cases} x'(t)=-y(t),\\ y'(t)=x(t),&\text{pour }t\in[0,4\pi]\\ x(0)=1,\\ y(0)=0. \end{cases} \)

🎯 Travail demandé : vérifier (analytiquement) que \(I(t)=x^2(t)+y^2(t)\) est un invariant pour le système.

🛠️ Partie 2 : Approximations Numériques

Choix des paramètres et notations :

• Nombre de points de discrétisation : \(N=193\)
  
• Pas de temps : \(h=t_{n+1}-t_n=\frac{\pi}{48}\)
  
• \(\mathbf{z}_n=(u_n,w_n)\) avec \(u_n\approx x_n=x(t_n)\) et \(w_n\approx y_n=y(t_n)\)
  
• \(J_n\approx I_n=I(t_n)\)

🎯 Travail demandé : implémenter les schémas ci-dessous et compléter l’analyse indiquée.

1. Méthode d’Euler explicite
   • Tracer \((t_n,u_n)\) et \((t_n,w_n)\) sur un même graphique.
     
   • Tracer \((t_n,J_n)\) sur un autre graphique.
     
   • Tracer \((u_n,w_n)\) (portrait de phase) et vérifier que la solution numérique diverge vers l’extérieur.
     
   • Montrer analytiquement que \(J_n=(1+h^2)^n\) et interpréter les résultats.
2. Méthode d’Euler implicite
   • Répéter les mêmes analyses que pour Euler explicite.
     
   • Remarque : la linéarité du second membre permet de rendre ce schéma explicite.
     
   • À faire : commenter les résultats et écrire l’expression analytique de \(J_n\).
3. Méthode de Crank-Nicolson
   • Répéter les mêmes étapes que précédemment.
     
   • Remarque : la linéarité du second membre permet également ici de rendre ce schéma explicite.
     
   • À faire : commenter les résultats et écrire l’expression analytique de \(J_n\).
4. Méthode avec odeint du module scipy.integrate
   • Appliquer la fonction odeint pour résoudre le système.
     
   • Analyser le comportement de l’invariant \(J_n\) et commenter les résultats.

🧩 Partie 3 : Solution exacte

Il est possible de calculer analytiquement la solution exacte dans ce cas particulier.

🎯 Travail demandé : utiliser le module sympy pour déterminer la solution exacte et comparer avec les solutions approchées.

Partie 1 : Invariant

Pour tout \(t\) on a

\( I'(t)=\left(x^2(t) + y^2(t)\right)' = 2x'(t)x(t)+2y'(t)y(t)=-2x(t)y(t)+2x(t)y(t)=0 \)

donc \(I(t)=I(0)=0^2+1^2=1\).

Partie 2 : Approximations

%reset -f
%matplotlib inline

import matplotlib.pyplot as plt
import numpy as np
plt.rcParams.update({<span class="st">'font.size'</span>: <span class="dv">12</span>}) 
# from scipy.optimize import fsolve # non necessaire car on resout l'equation implicite a la main

import sympy as sym
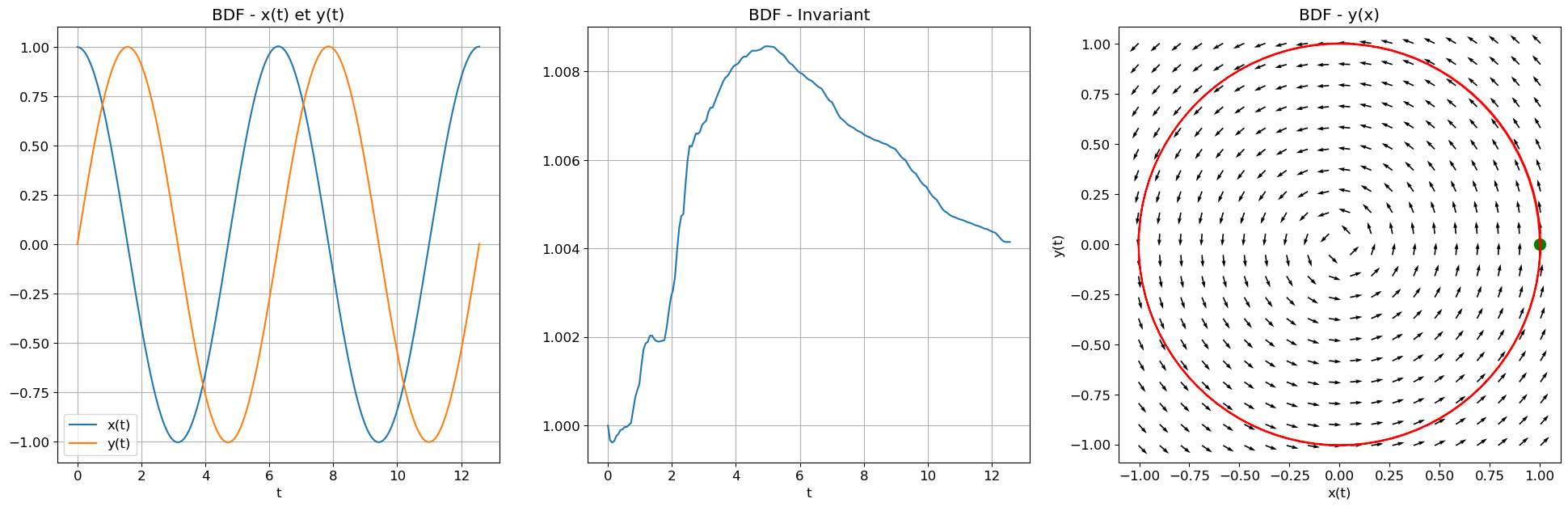
sym.init_printing()

t0 = 0
tfinal = 4*np.pi


N = 192 #*100
tt = np.linspace(0, tfinal, N+1)  # np.arange(t0, tfinal+h/2, h)


# Notation vectorielle
# ====================

# CI (2 conditions)
zz0 = np.array([1,0])

# EDO (2 equations) 
# phi : RxR^2 -> R^2
phi = lambda t,zz : np.array( [ -zz[1], zz[0] ] )

Pour simplifier les affichages, on définit une fonction affichage qui affiche les graphes de \(u_n\) et \(w_n\) en fonction de \(t_n\), le graphe de \(J_n\) et enfin le portrait de phase \((u_n,w_n)\). Il suffira alors d’appeler cette fonction pour chaque schéma.

def affichage(zz, JJ, tt, zz0, phi, schema):
    
    # zz[:, 0] = x(t) [vecteur uu]
    # zz[:, 1] = y(t) [vecteur ww]
    
    plt.figure(figsize=(24, 7))

    # Graphe de x(t) et y(t)
    plt.subplot(1, 3, 1)
    plt.plot(tt, zz[:, 0], label='x(t)')
    plt.plot(tt, zz[:, 1], label='y(t)')
    plt.grid()
    plt.xlabel('t')
    plt.legend()
    plt.title(f'{</span>schema<span class="sc">} - x(t) et y(t)')

    # Graphe de l'invariant JJ
    plt.subplot(1, 3, 2)
    plt.plot(tt, JJ)
    plt.grid()
    plt.xlabel('t')
    plt.title(f'{</span>schema<span class="sc">} - Invariant')

    # Diagramme de phase y(x)
    plt.subplot(1, 3, 3)
    u_min, u_max = min(zz[:, 0]), max(zz[:, 0])
    w_min, w_max = min(zz[:, 1]), max(zz[:, 1])
    Y1, Y2 = np.meshgrid(np.linspace(u_min, u_max, 20), np.linspace(w_min, w_max, 20))
    
    # Calcul du champ de vecteurs
    V = np.array([phi(0, [y1, y2]) for y1, y2 in zip(Y1.flatten(), Y2.flatten())])
    V1 = V[:, 0].reshape(Y1.shape)
    V2 = V[:, 1].reshape(Y2.shape)
    r = np.sqrt(V1**2 + V2**2)
    
    # Affichage du champ et des trajectoires
    plt.quiver(Y1, Y2, V1 / r, V2 / r)  
    plt.plot(zz[:, 0], zz[:, 1], 'r')
    plt.scatter(zz[0, 0], zz[0, 1], c='g', s=100)  # point initial
    plt.xlabel('x(t)')
    plt.ylabel('y(t)')
    plt.title(f'{</span>schema<span class="sc">} - y(x)')
    plt.axis('equal')
    plt.show()

Euler explicite

\( \begin{cases} u_0=1,\\ w_0=0,\\ u_{n+1}=u_n+h\varphi_1(t_n,u_n,w_n),\\ w_{n+1}=w_n+h\varphi_2(t_n,u_n,w_n) \end{cases} \)

def EE(phi,tt,zz0):
    nb_eq = len(zz0) # nombre d'équations
    N = len(tt)-1 # N+1 points, donc N intervalles
    zz = np.zeros((N+1,nb_eq)) # colonnes = variables, lignes = temps
    zz[0] = zz0
    h = tt[1]-tt[0]
    for n in range(N):
        zz[n+1] = zz[n]+h*phi(tt[n],zz[n])
    return zz


# Version qui retourne un tableau 1D si zz0 est scalaire
# def EE(phi, tt, zz0):
#     zz0 = np.atleast_1d(zz0)  # Convertir zz0 en tableau (même si scalaire)
#     nb_eq = len(zz0)  # Nombre d'équations
#     N = len(tt) - 1  # N+1 points, donc N intervalles
#     zz = np.zeros((N + 1, nb_eq))  # Colonnes = variables, lignes = temps
#     zz[0] = zz0
#     h = tt[1] - tt[0]
#     for n in range(N):
#         zz[n + 1] = zz[n] + h * phi(tt[n], zz[n])
#     if nb_eq == 1:
#         return zz.flatten()  # Retourner un tableau 1D si scalaire
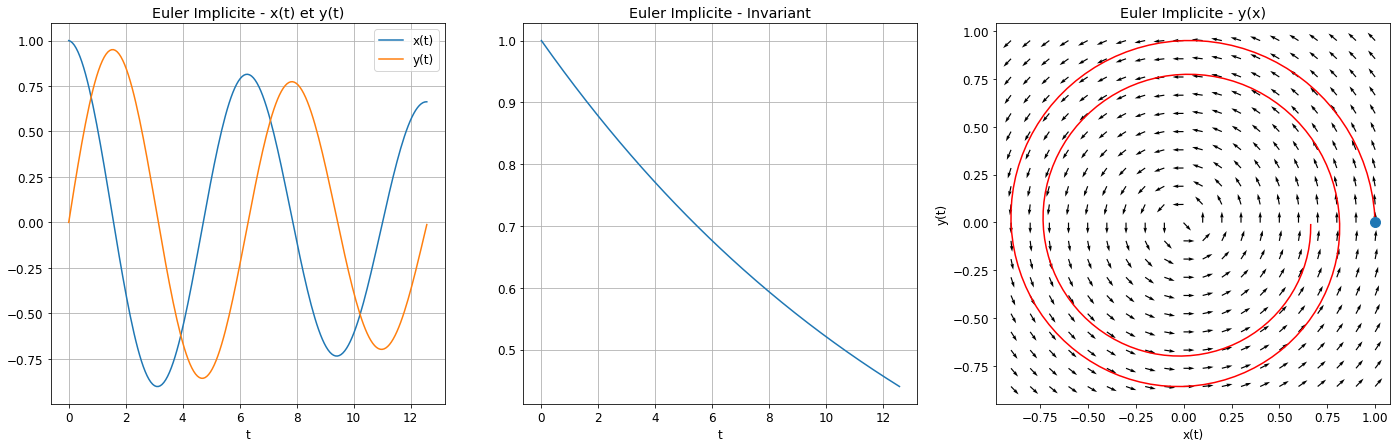
#     return zz

On remarque que

\( \begin{cases} u_0=1,\\ w_0=0,\\ u_{n+1}=u_n-hw_n,\\ w_{n+1}=w_n+hu_n \end{cases} \)

On a

\( J_{n+1} =u_{n+1}^2+w_{n+1}^2 =(u_n-hw_n)^2+(w_n+hu_n)^2 =(1+h^2)(u_n^2+w_n^2) =(1+h^2)J_n \)

soit encore

\( J_n=(1+h^2)^nJ_0=(1+h^2)^n. \)

On voit que

• l’invariant n’est conservé que si \(h=0\), ce qui est impossible,
• pour \(h\) fixé, \(\lim\limits_{n\to+\infty}J_n=+\infty\) (comportement pour \(t\to\infty\)),
• pour \(n\) fixé, l’erreur \(|J_n-I_n|\) diminue comme \(h^2\) (convergence sur un intervalle fixé).

zz_ep = EE(phi,tt,zz0) # N+1 lignes, 2 colonnes
uu_ep, ww_ep = zz_ep.T
JJ_ep = uu_ep**2+ww_ep**2
affichage(zz_ep, JJ_ep, tt, zz0, phi, 'Euler Explicite')

Euler implicite

\( \begin{cases} u_0=1,\\ w_0=0,\\ u_{n+1}=u_n+h\varphi_1(t_{n+1},u_{n+1},w_{n+1})=u_n-hw_{n+1},\\ w_{n+1}=w_n+h\varphi_2(t_{n+1},u_{n+1},w_{n+1})=w_n+hu_{n+1} \end{cases} \)

En résolvant le système linéaire on obtient une écriture explicite

\( \begin{cases} u_0=1,\\ w_0=0,\\ u_{n+1}=\dfrac{u_n-hw_{n}}{1+h^2},\\ w_{n+1}=\dfrac{w_n+hu_{n}}{1+h^2}. \end{cases} \)

def EI(phi,tt,zz0): 
    nb_eq = len(zz0) # nombre d'équations
    N = len(tt)-1 # N+1 points, donc N intervalles
    zz = np.zeros((N+1,nb_eq))
    zz[0] = zz0
    h = tt[1]-tt[0]
    for n in range(N):
        zz[n+1,0] = (zz[n,0]-h*zz[n,1])/(1+h**2)
        zz[n+1,1] = (zz[n,1]+h*zz[n,0])/(1+h**2)
    return zz

#  VERSION AVEC fsolve (non demandé)
from scipy.optimize import fsolve

def EI_bis(phi,tt,zz0):
    nb_eq = len(zz0) # nombre d'équations
    N = len(tt)-1 # N+1 points, donc N intervalles
    zz = np.zeros((N+1,nb_eq))
    zz[0] = zz0
    h = tt[1]-tt[0]
    for n in range(N):
        system = lambda z : z - zz[n] - h*phi(tt[n+1],z)
        zz[n+1] = fsolve( system , zz[n] ) 
    return zz


# Version qui retourne un tableau 1D si zz0 est scalaire
# def EI_bis(phi, tt, zz0):
#     zz0 = np.atleast_1d(zz0)  # Convertir zz0 en tableau (même si scalaire)
#     nb_eq = len(zz0)  # Nombre d'équations
#     N = len(tt) - 1  # N+1 points, donc N intervalles
#     zz = np.zeros((N + 1, nb_eq))
#     zz[0] = zz0
#     h = tt[1] - tt[0]
#     for n in range(N):
#         system = lambda z: z - zz[n] - h * phi(tt[n + 1], z)
#         zz[n + 1] = fsolve(system, zz[n])
#     if nb_eq == 1:
#         return zz.flatten()  # Retourner un tableau 1D si scalaire
#     return zz

On a

\( J_{n+1} =u_{n+1}^2+w_{n+1}^2 =\frac{(u_n-hw_n)^2+(w_n+hu_n)^2}{(1+h^2)^2} =(u_n^2+w_n^2)\frac{1+h^2}{(1+h^2)^2} =\frac{1+h^2}{(1+h^2)^2}J_n =\frac{1}{1+h^2}J_n \)

soit encore

\( J_n=\left(\frac{1}{1+h^2}\right)^nJ_0=\left(\frac{1}{1+h^2}\right)^n. \)

On voit que

• l’invariant n’est conservé que si \(h=0\), ce qui est impossible,
• pour \(h\) fixé, \(\lim\limits_{n\to+\infty}J_n=0^+\),
• pour \(n\) fixé, l’erreur \(|J_n-I_n|\) diminue comme \(h^2\).

# zz_er = EI(phi,tt,zz0)
zz_er = EI_bis(phi,tt,zz0)
uu_er, ww_er = zz_er.T
JJ_er = uu_er**2+ww_er**2
affichage(zz_er, JJ_er, tt, zz0, phi, 'Euler Implicite')

Crank Nicolson

\( \begin{cases} u_0=1,\\ w_0=0,\\ u_{n+1}=u_n+\frac{h}{2}\Big(\varphi_1(t_{n},u_{n},w_{n})+\varphi_1(t_{n+1},u_{n+1},w_{n+1})\big)=u_n-\frac{h}{2}w_{n}-\frac{h}{2}w_{n+1},\\ w_{n+1}=w_n+\frac{h}{2}\Big(\varphi_2(t_{n},u_{n},w_{n})+\varphi_2(t_{n+1},u_{n+1},w_{n+1})\big)=w_n+\frac{h}{2}u_{n}+\frac{h}{2}u_{n+1}. \end{cases} \)

En résolvant le système linéaire on obtient une écriture explicite :

\( \begin{cases} u_0=1,\\ w_0=0,\\ u_{n+1}=\dfrac{(4-h^2)u_n-4hw_{n}}{4+h^2},\\ w_{n+1}=\dfrac{(4-h^2)w_n+4hu_{n}}{4+h^2}. \end{cases} \)

De plus, on a

\( \begin{aligned} J_{n+1} &=u_{n+1}^2+w_{n+1}^2 \\ &=\frac{((4-h^2)u_n-4hw_n)^2+((4-h^2)w_n+4hu_n)^2}{(4+h^2)^2} \\ &=\frac{(4-h^2)^2u_n^2+16h^2w_n^2-8(4-h^2)hu_nw_n+(4-h^2)^2w_n^2+16h^2u_n^2+8(4-h^2)hu_nw_n}{(4+h^2)^2} \\ &=\frac{\big((4-h^2)^2+16h^2\big)(u_n^2+w_n^2)}{(4+h^2)^2} \\ &=\frac{(4+h^2)^2(u_n^2+w_n^2)}{(4+h^2)^2} \\ &=(u_n^2+w_n^2)=J_n \end{aligned} \)

On voit que l’invariant est conservé pour tout \(h\)

Vérifions ces calculs avec sympy:

dt = sym.Symbol('h') # pour ne pas redefinir h comme un symbole, on écrit dt mais on affiche h
u_n = sym.Symbol('u_n')
u_np1 = sym.Symbol('u_{n+1}')
w_n = sym.Symbol('w_n')
w_np1 = sym.Symbol('w_{n+1}')

eq1 = sym.Eq( u_np1 , u_n-dt/2*w_n-dt/2*w_np1 )
eq2 = sym.Eq( w_np1 , w_n+dt/2*u_n+dt/2*u_np1 )
sol = sym.solve([eq1,eq2],[u_np1,w_np1],dict=True)[0]
display(sol)

J_np1 = u_np1**2+w_np1**2
J_np1.subs(sol).simplify()

\(\displaystyle \left\{ u_{n+1} : \frac{- h^{2} u_{n} - 4 h w_{n} + 4 u_{n}}{h^{2} + 4}, \ w_{n+1} : \frac{- h^{2} w_{n} + 4 h u_{n} + 4 w_{n}}{h^{2} + 4}\right\}\)

\(\displaystyle u_{n}^{2} + w_{n}^{2}\)

def cn(phi,tt,zz0):
    nb_eq = len(zz0) # nombre d'équations
    N = len(tt)-1 # N+1 points, donc N intervalles
    zz = np.zeros((N+1,nb_eq))
    zz[0] = zz0
    h = tt[1]-tt[0]
    for n in range(N):
        zz[n+1,0] = ((4-h**2)*zz[n,0]-4*h*zz[n,1])/(4+h**2)
        zz[n+1,1] = ((4-h**2)*zz[n,1]+4*h*zz[n,0])/(4+h**2)
    return zz

#  VERSION AVEC fsolve (non demandé)
from scipy.optimize import fsolve

def cn_bis(phi,tt,zz0):
    nb_eq = len(zz0) # nombre d'équations
    N = len(tt)-1 # N+1 points, donc N intervalles
    zz = np.zeros((N+1,nb_eq))
    zz[0] = zz0
    h = tt[1]-tt[0]
    for n in range(N):
        system = lambda z : z - zz[n] - h/2*( phi(tt[n],zz[n]) + phi(tt[n+1],z) )
        zz[n+1] = fsolve( system , zz[n] ) 
    return zz

# Version qui retourne un tableau 1D si zz0 est scalaire
# def cn_bis(phi, tt, zz0):
#     zz0 = np.atleast_1d(zz0)  # Convertir zz0 en tableau (même si scalaire)
#     nb_eq = len(zz0)  # Nombre d'équations
#     N = len(tt) - 1  # N+1 points, donc N intervalles
#     zz = np.zeros((N + 1, nb_eq))
#     zz[0] = zz0
#     h = tt[1] - tt[0]
#     for n in range(N):
#         system = lambda z: z - zz[n] - h / 2 * (phi(tt[n], zz[n]) + phi(tt[n + 1], z))
#         zz[n + 1] = fsolve(system, zz[n])
#     if nb_eq == 1:
#         return zz.flatten()  # Retourner un tableau 1D si scalaire
#     return zz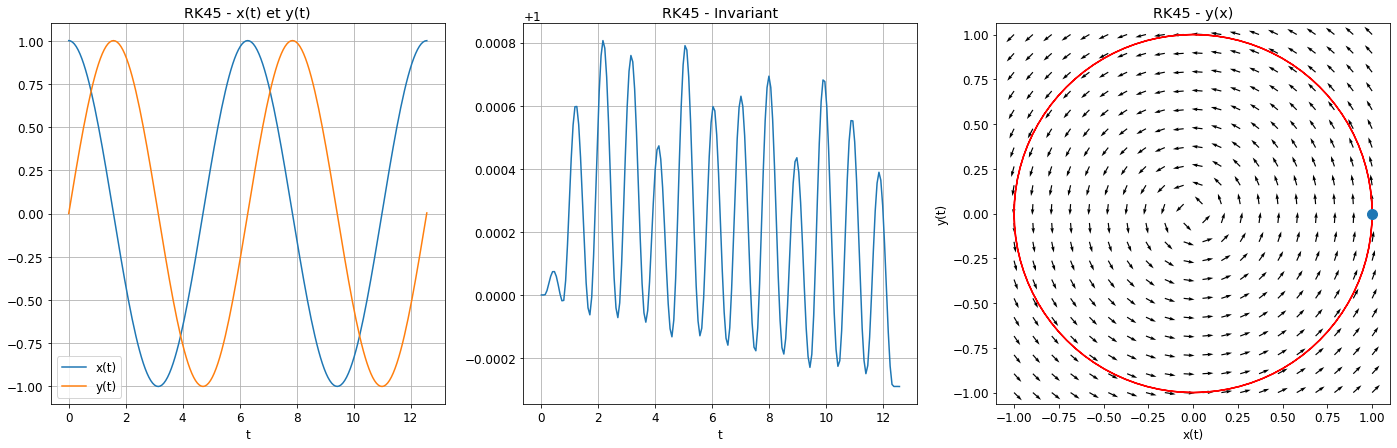

# zz_cn = cn(phi,tt,zz0)
zz_cn = cn_bis(phi,tt,zz0)
uu_cn, ww_cn = zz_cn.T
JJ_cn = uu_cn**2+ww_cn**2
affichage(zz_cn, JJ_cn, tt, zz0, phi, 'Crank Nicolson')

Avec odeint du module scipy.integrate:

from scipy.integrate import odeint

zz_odeint = odeint(phi,zz0,tt,tfirst=True)
uu_odeint, ww_odeint = zz_odeint.T

JJ_odeint = uu_odeint**2+ww_odeint**2
affichage(zz_odeint, JJ_odeint, tt, zz0, phi, 'odeint')

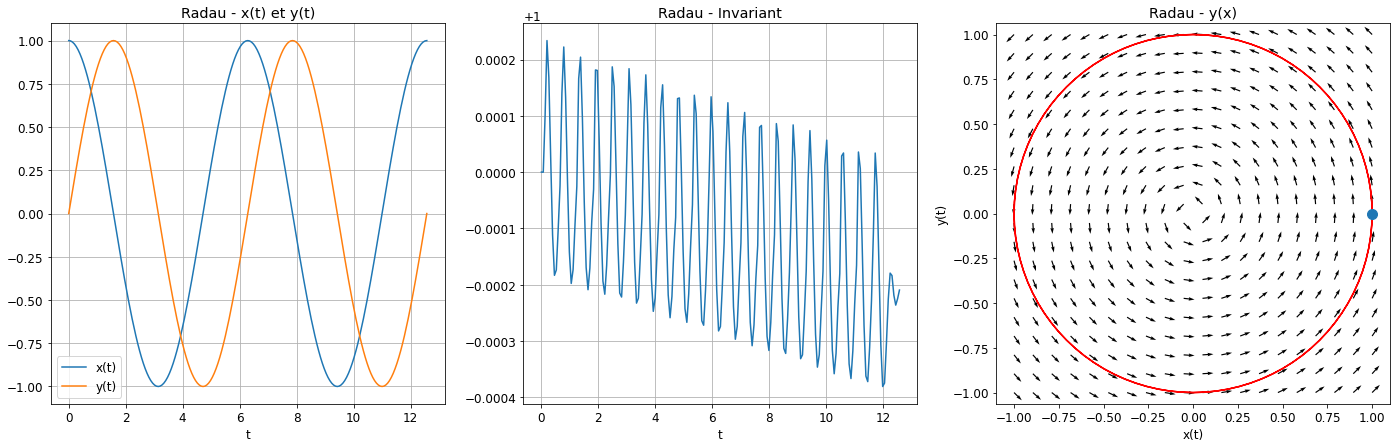
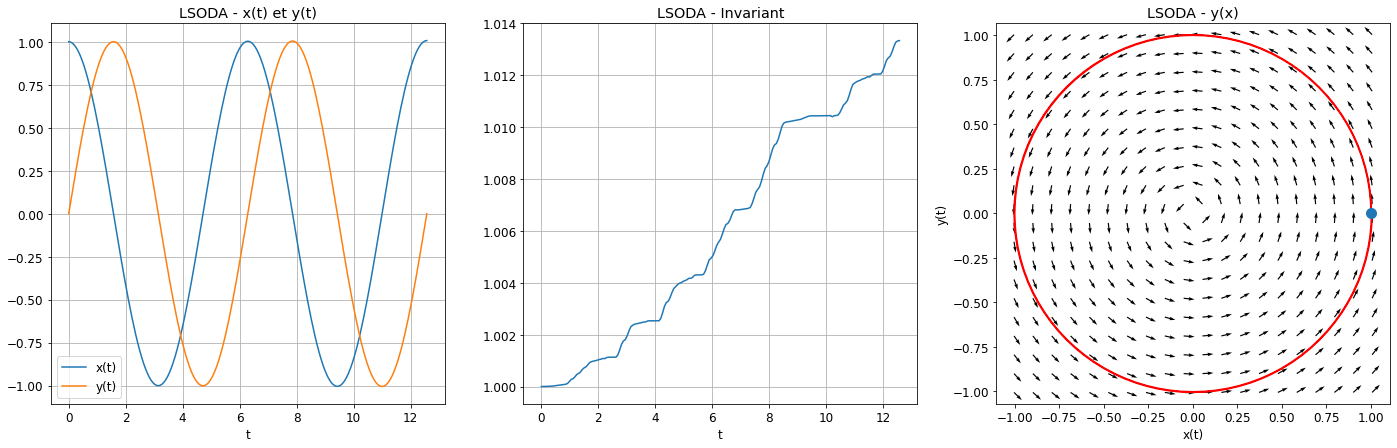
Bonus : avec solve_ivp du module scipy.integrate:

from scipy.integrate import solve_ivp

sol_RK45 = solve_ivp(phi,[t0,tfinal],zz0,t_eval=tt, method='RK45')
uu_RK45, ww_RK45 = sol_RK45.y

JJ_RK45 = uu_RK45**2+ww_RK45**2

affichage(sol_RK45.y.T, JJ_RK45, tt, zz0, phi, 'RK45')

sol_Radau = solve_ivp(phi,[t0,tfinal],zz0,t_eval=tt, method='Radau')
uu_Radau, ww_Radau = sol_Radau.y

JJ_Radau = uu_Radau**2+ww_Radau**2

affichage(sol_Radau.y.T, JJ_Radau, tt, zz0, phi, 'Radau')

sol_BDF = solve_ivp(phi,[t0,tfinal],zz0,t_eval=tt, method='BDF')
uu_BDF, ww_BDF = sol_BDF.y

JJ_BDF = uu_BDF**2+ww_BDF**2

affichage(sol_BDF.y.T, JJ_BDF, tt, zz0, phi, 'BDF')

sol_LSODA = solve_ivp(phi,[t0,tfinal],zz0,t_eval=tt, method='LSODA')
uu_LSODA, ww_LSODA = sol_LSODA.y

JJ_LSODA = uu_LSODA**2+ww_LSODA**2

affichage(sol_LSODA.y.T, JJ_LSODA, tt, zz0, phi, 'LSODA')

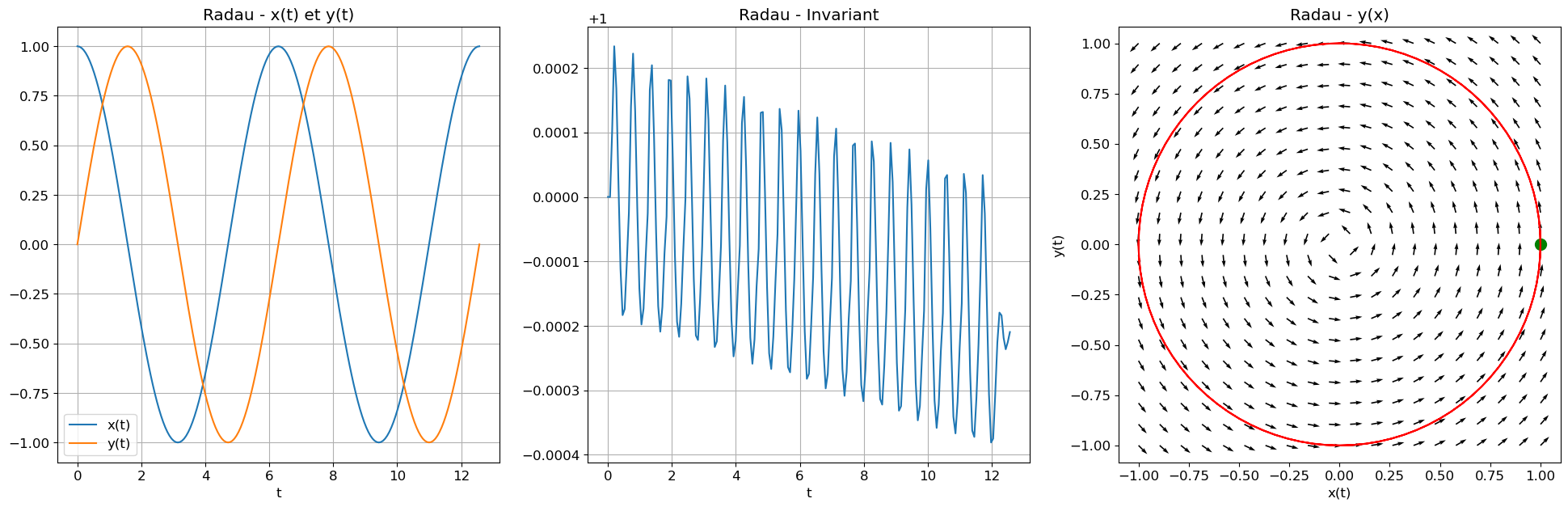
Partie 3 : Solution exacte

La solution exacte est

\(\begin{align*} x(t)&=\cos(t),\\ y(t)&=\sin(t). \end{align*}\)

Cette solution est périodique de période \(2\pi\) et on a bien

\( I(t)=x^2(t) + y^2(t) = 1 \quad \forall t. \)

Vérifions-le avec le module sympy:

t = sym.Symbol('t')
x = sym.Function('x')
y = sym.Function('y')

t_0 = 0
x_0 = zz0[0]
y_0 = zz0[1]


edo1 = sym.Eq( sym.diff(x(t),t) , -y(t) )
edo2 = sym.Eq( sym.diff(y(t),t) , x(t) )
display(edo1)
display(edo2)


solpar_1, solpar_2 = sym.dsolve([edo1,edo2],[x(t),y(t)], ics={x(t_0): x_0, y(t_0): y_0})


# AFFICHAGE
func_1 = sym.lambdify(t,solpar_1.rhs,'numpy')
func_2 = sym.lambdify(t,solpar_2.rhs,'numpy')

tt = np.linspace(0,4*np.pi,193)
xx = func_1(tt)
yy = func_2(tt)
JJ = xx**2+yy**2

affichage(np.array([xx,yy]).T, JJ, tt, zz0, phi, 'Solution exacte')

\(\displaystyle \frac{d}{d t} x{\left(t \right)} = - y{\left(t \right)}\)

\(\displaystyle \frac{d}{d t} y{\left(t \right)} = x{\left(t \right)}\)