Calculs 🐍 analytiques 🐍 avec le module sympy
En L1 vous avez appris comment calculer la solution générale de quelques équations différentielles ordinaires (EDO). Nous allons maintenant voir comment automatiser ces calculs avec le module sympy conçu pour du calcul symbolique/formel/exact.
Cf. https://docs.sympy.org/latest/modules/solvers/ode.html
Bien lire et comprendre les deux exemples pour résoudre des EDO du premier ordre et des systèmes d’EDO du premier ordre, puis résoudre les deux exercices proposés.
- Exemples :
- EDO du premier ordre
- système d’EDO du premier ordre
- EDO d’ordre 2
- Exercices
- EDO du premier ordre
- Système d’EDO du premier ordre
1 Exemple de résolution analytique d’une équation différentielle d’ordre 1
Considérons le problème de Cauchy
\(
\begin{cases}
u'(x)=-3x^2u(x)+6x^2,\\
u(0)=4.
\end{cases}
\)
On peut résoudre ce problème de Cauchy de manière analytique en utilisant le module sympy de la manière suivante.
Définition du problème de Cauchy :
Code
# Variables
x = sym.Symbol('x')
u = sym.Function('u')
# Equation différentielle
left = sym.diff(u(x),x) # la dérivée de u par rapport à x
right = 6*x**2-3*x**2*u(x) # l'expression de l'équation différentielle
edo = sym.Eq( left , right ) # l'équation différentielle
display(edo)
# Conditions initiales
x0 = 0
u0 = 4
display(sym.Eq(u(x0),u0))\(\displaystyle \frac{d}{d x} u{\left(x \right)} = - 3 x^{2} u{\left(x \right)} + 6 x^{2}\)
\(\displaystyle u{\left(0 \right)} = 4\)
Calcul de la solution exacte (2 méthodes : une méthode directe et une méthode pas à pas) :
Code
- Méthode 1 : méthode directe
\(\displaystyle u{\left(x \right)} = 2 + 2 e^{- x^{3}}\)
Code
# Méthode 2 : méthode pas-à-pas
# ==============================
# On va calculer la solution générale, puis la solution particulière en prenant en compte la condition initiale
display(Markdown("- Méthode 2 : méthode pas-à-pas"))
# Étape 1 : calcul de la solution générale (qui contient la constante d'intégration) :
solgen = sym.dsolve(edo,u(x))
display(solgen)
# Étape 2 : calcul de la constante d'intégration en prenant en compte la condition initiale :
cond_init = sym.Eq( u0, solgen.rhs.subs(x,x0) )
display(cond_init)
consts = sym.solve( cond_init , dict=True)[0]
display(consts)
# Étape 3 : calcul de la solution particulière :
solpar = solgen.subs(consts)
display(solpar)- Méthode 2 : méthode pas-à-pas
\(\displaystyle u{\left(x \right)} = C_{1} e^{- x^{3}} + 2\)
\(\displaystyle 4 = C_{1} + 2\)
\(\displaystyle \left\{ C_{1} : 2\right\}\)
\(\displaystyle u{\left(x \right)} = 2 + 2 e^{- x^{3}}\)
Conversion en une fonction de numpy et affichage :
Code
# Transformation en fonction numpy
func = sym.lambdify(x,solpar.rhs,'numpy')
# Tracé de la solution
import matplotlib.pyplot as plt
import numpy as np
# plt.rcdefaults()
plt.rcParams.update({<span class="st">'font.size'</span>: <span class="dv">16</span>})
plt.figure(figsize=(10,7))
xx = np.linspace(0,3,101)
yy = func(xx)
plt.plot(xx,yy)
plt.xlabel('x')
plt.ylabel('u')
plt.grid();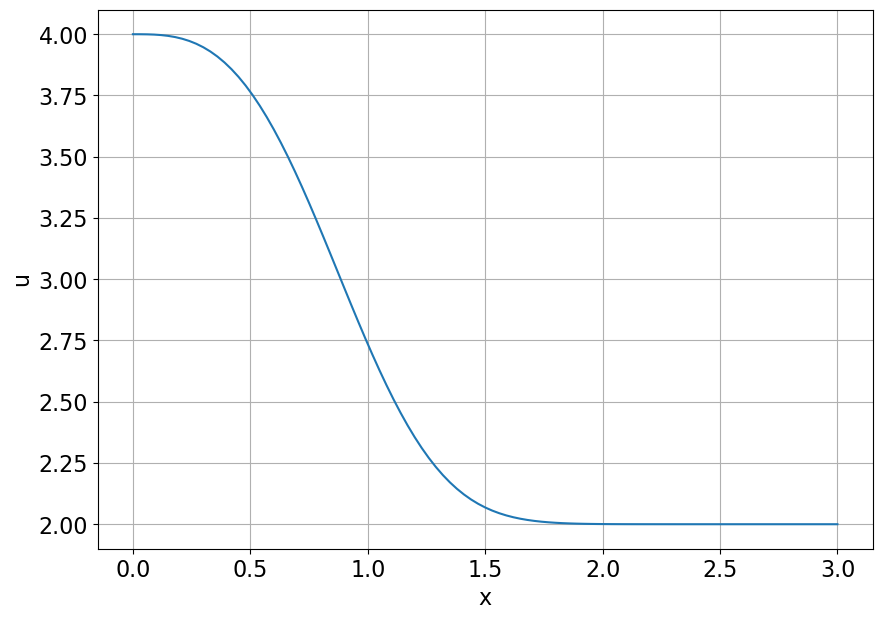
2 Exemple de résolution analytique d’un système d’équations différentielles d’ordre 1
\( \begin{pmatrix} y_1\\ y_2 \end{pmatrix}'(t) = \begin{pmatrix} \varphi_1(t, y_1(t),y_2(t))\\ \varphi_2(t, y_1(t),y_2(t)) \end{pmatrix} = \begin{pmatrix} y_1(t)-y_2(t)\\ y_2(t)-y_1(t) \end{pmatrix} \)
avec \(t\in[0;10]\) et en prenant comme condition initiale le vecteur \(\mathbf{y}_0=(2,1)\).
Code
import sympy as sym
sym.init_printing()
# Variables
t = sym.Symbol('t')
# Fonctions inconnues
y1 = sym.Function(r'y_1')
y2 = sym.Function(r'y_2')
# Termes de droite
right1 = y1(t)-y2(t)
right2 = y2(t)-y1(t)
# Équations différentielles
edo1 = sym.Eq( sym.diff(y1(t),t) , right1 )
edo2 = sym.Eq( sym.diff(y2(t),t) , right2 )
display(edo1)
display(edo2)
# Conditions initiales
t0 = 0
y1_0 = 2
y2_0 = 1
display(sym.Eq(y1(t0),y1_0))
display(sym.Eq(y2(t0),y2_0))\(\displaystyle \frac{d}{d t} y_{1}{\left(t \right)} = y_{1}{\left(t \right)} - y_{2}{\left(t \right)}\)
\(\displaystyle \frac{d}{d t} y_{2}{\left(t \right)} = - y_{1}{\left(t \right)} + y_{2}{\left(t \right)}\)
\(\displaystyle y_{1}{\left(0 \right)} = 2\)
\(\displaystyle y_{2}{\left(0 \right)} = 1\)
Code
# Méthode 1 : méthode directe
# ============================
solpar_1, solpar_2 = sym.dsolve( [ edo1, edo2 ] ,
ics = { y1(t0):y1_0, y2(t0):y2_0 } )
display(solpar_1)
display(solpar_2)
# Méthode 2 : méthode pas-à-pas
# ==============================
# solgen = sym.dsolve([edo1,edo2],[y1(t),y2(t)])
# display(solgen)
# consts = sym.solve( [sym.Eq( y1_0, solgen[0].rhs.subs(t,t0)) ,
# sym.Eq( y2_0, solgen[1].rhs.subs(t,t0)) ] , dict=True)[0]
# display(consts)
# solpar_1 = solgen[0].subs(consts)
# solpar_2 = solgen[1].subs(consts)
# display(solpar_1)
# display(solpar_2)\(\displaystyle y_{1}{\left(t \right)} = \frac{e^{2 t}}{2} + \frac{3}{2}\)
\(\displaystyle y_{2}{\left(t \right)} = \frac{3}{2} - \frac{e^{2 t}}{2}\)
Code
# Affichage
# =========
# Transformation des solutions en fonctions numpy
func_1 = sym.lambdify(t,solpar_1.rhs,'numpy')
func_2 = sym.lambdify(t,solpar_2.rhs,'numpy')
# Plot
import matplotlib.pyplot as plt
import numpy as np
# plt.rcdefaults()
plt.rcParams.update({<span class="st">'font.size'</span>: <span class="dv">16</span>})
plt.figure(figsize=(18,7))
tt = np.linspace(0,3,101)
yy_1 = func_1(tt)
yy_2 = func_2(tt)
plt.subplot(1,2,1)
plt.plot(tt,yy_1,tt,yy_2)
plt.legend([r'$y_1$',r'$y_2$'])
plt.xlabel(r'$t$')
plt.ylabel(r'$y$')
plt.title("Solutions")
plt.subplot(1,2,2)
plt.plot(yy_1,yy_2)
plt.xlabel(r'$y_1$')
plt.ylabel(r'$y_2$')
plt.title("Portrait de phase");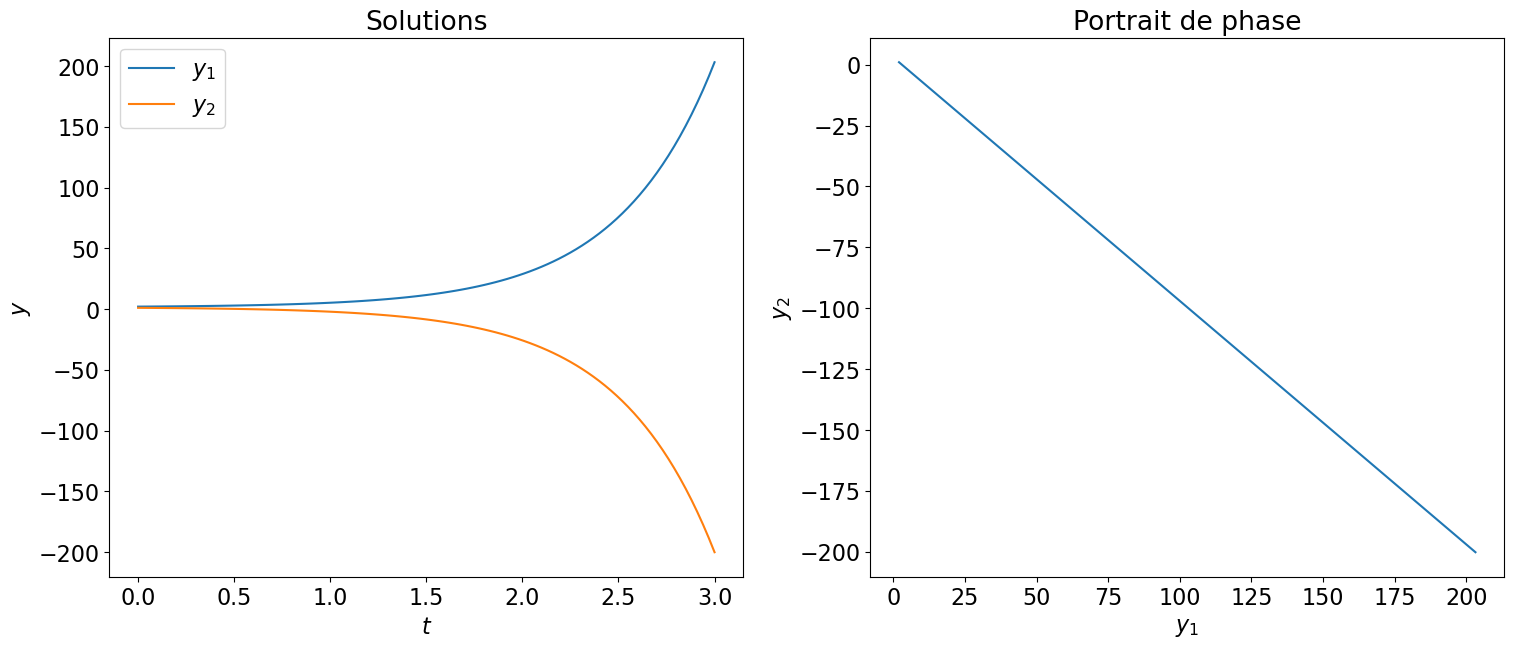
3 Exemple de résolution analytique d’une équation différentielle d’ordre 2
Calculons l’unique solution du problème de Cauchy
\( \begin{cases} y''(t) + 2y'(t) + 2y(t) = 2\sin(t), &t>0\\ y(0)=1,\\ y'(0)=0. \end{cases} \)
- D’abord avec la méthode directe en définissant l’équation différentielle d’ordre 2 et les conditions initiales.
- Ensuite avec la méthode pas à pas en définissant l’équation différentielle d’ordre 2 et les conditions initiales.
- Enfin, en transformant l’équation différentielle d’ordre 2 en un système d’équations différentielles d’ordre 1 (voir l’exercice précédent) et en utilisant la méthode pas à pas.
Méthode directe sur l’équation différentielle d’ordre 2 :
Code
import sympy as sym
sym.init_printing()
# Variables
t = sym.Symbol('t')
# Fonction inconnue
y = sym.Function('y')
# Équation différentielle
left = sym.diff(y(t),t,2) + 2*sym.diff(y(t),t) + 2*y(t)
right = 2*sym.sin(t)
edo = sym.Eq( left , right ) # l'équation différentielle
display(edo)
# Conditions initiales
t0 = 0
y0 = 1
yp0 = 0
display(sym.Eq(y(t0),y0))
display(sym.Eq(sym.diff(y(t),t).subs(t,t0),yp0))
# Méthode 1 : méthode directe
# ============================
solpar = sym.dsolve(edo,y(t), ics={y(t0):y0, sym.diff(y(t),t).subs(t,t0):yp0})
display(solpar)\(\displaystyle 2 y{\left(t \right)} + 2 \frac{d}{d t} y{\left(t \right)} + \frac{d^{2}}{d t^{2}} y{\left(t \right)} = 2 \sin{\left(t \right)}\)
\(\displaystyle y{\left(0 \right)} = 1\)
\(\displaystyle \left. \frac{d}{d t} y{\left(t \right)} \right|_{\substack{ t=0 }} = 0\)
\(\displaystyle y{\left(t \right)} = \left(\frac{7 \sin{\left(t \right)}}{5} + \frac{9 \cos{\left(t \right)}}{5}\right) e^{- t} + \frac{2 \sin{\left(t \right)}}{5} - \frac{4 \cos{\left(t \right)}}{5}\)
Vérifions si elle satisfait bien notre problème de Cauchy :
Code
# Qua donne la solution trouvée lorsqu'on la remplace dans l'équation différentielle ?
display( (sym.diff(solpar.rhs,t,2) + 2*sym.diff(solpar.rhs,t) + 2*solpar.rhs -2*sym.sin(t) ).simplify() )
# Que vaut la solution trouvée lorsqu'on la remplace dans les conditions initiales ?
display( solpar.rhs.subs(t,t0) )
display( sym.diff(solpar.rhs,t).subs(t,t0) )\(\displaystyle 0\)
\(\displaystyle 1\)
\(\displaystyle 0\)
Code
# Affichage de la solution
func = sym.lambdify(t,solpar.rhs,'numpy')
import matplotlib.pyplot as plt
import numpy as np
tt = np.linspace(0,10,1001)
yy = func(tt)
plt.figure(figsize=(15,7))
# Solution
# ========
plt.subplot(1,2,1)
plt.plot(tt,yy)
plt.title(r"$t\mapsto y(t)$")
plt.grid();
# Portraits de phase
# ==================
plt.subplot(1,2,2)
plt.plot(yy,np.gradient(yy,tt))
plt.title(r"$y\mapsto y'(y)$")
plt.grid();
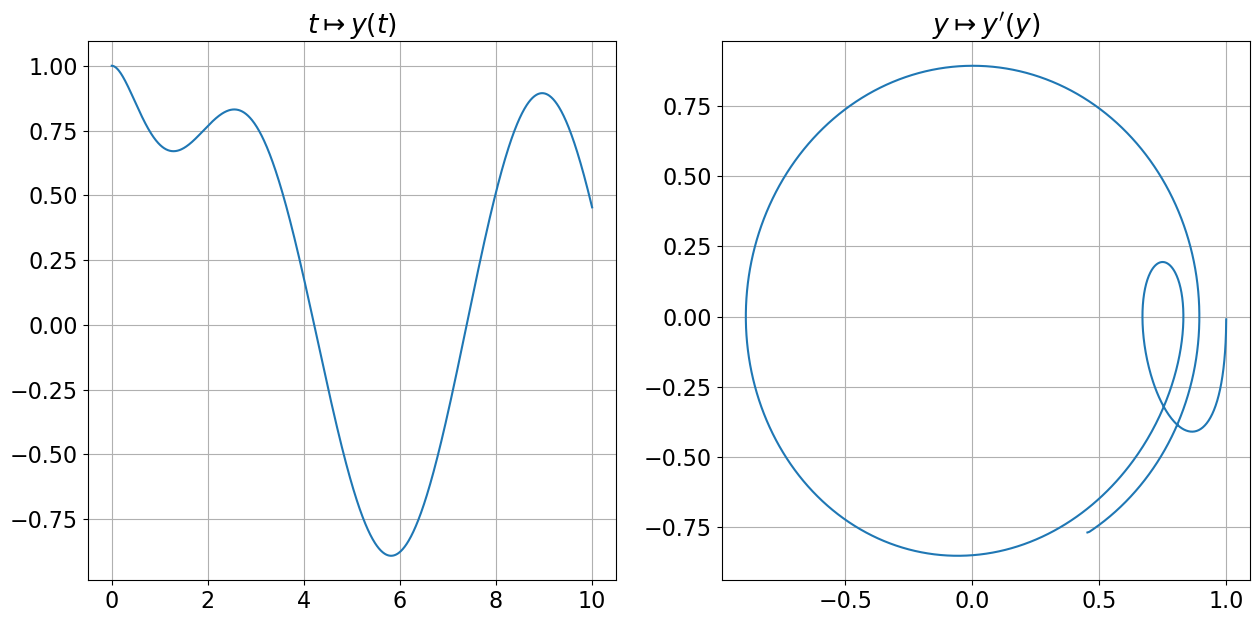
Méthode pas à pas sur l’équation différentielle d’ordre 2 :
Code
# Bonus : résolution de l'équation différentielle avec la méthode pas-à-pas
# ========================================================================
# Étape 1 : calcul de la solution générale (qui contient la constante d'intégration) :
solgen = sym.dsolve(edo,y(t))
display(solgen)
# Étape 2 : calcul de la constante d'intégration en prenant en compte les conditions initiales :
cond_init1 = sym.Eq( y0, solgen.rhs.subs(t,t0) )
cond_init2 = sym.Eq( yp0, sym.diff(solgen.rhs,t).subs(t,t0) )
display(cond_init1)
display(cond_init2)
consts = sym.solve( [cond_init1,cond_init2] , dict=True)[0]
display(consts)
# Étape 3 : calcul de la solution particulière :
solpar = solgen.subs(consts)
display(solpar)\(\displaystyle y{\left(t \right)} = \left(C_{1} \sin{\left(t \right)} + C_{2} \cos{\left(t \right)}\right) e^{- t} + \frac{2 \sin{\left(t \right)}}{5} - \frac{4 \cos{\left(t \right)}}{5}\)
\(\displaystyle 1 = C_{2} - \frac{4}{5}\)
\(\displaystyle 0 = C_{1} - C_{2} + \frac{2}{5}\)
\(\displaystyle \left\{ C_{1} : \frac{7}{5}, \ C_{2} : \frac{9}{5}\right\}\)
\(\displaystyle y{\left(t \right)} = \left(\frac{7 \sin{\left(t \right)}}{5} + \frac{9 \cos{\left(t \right)}}{5}\right) e^{- t} + \frac{2 \sin{\left(t \right)}}{5} - \frac{4 \cos{\left(t \right)}}{5}\)
Méthode directe ou pas à pas après transformation en un système d’équations différentielles d’ordre 1 :
Code
# Bonus : transformation en un système d'équations différentielles du premier ordre
# ================================================================================
# Variables
t = sym.Symbol('t')
y = sym.Function('y')
z = sym.Function('z')
# Équations
edo1 = sym.Eq( sym.diff(y(t),t) , z(t) )
edo2 = sym.Eq( sym.diff(z(t),t) , 2*sym.sin(t) - 2*z(t) - 2*y(t) )
display(edo1)
display(edo2)
# Conditions initiales
t0 = 0
y0 = 1
yp0 = 0
display(sym.Eq(y(t0),y0))
display(sym.Eq(z(t0),yp0))
# Méthode 1 : méthode directe
# ============================
display(Markdown("- Méthode 1 : méthode directe"))
solpar = sym.dsolve( [edo1,edo2], [y(t),z(t)], ics={y(t0):y0, z(t0):yp0} )
display(solpar)
# Méthode 2 : méthode pas-à-pas
# ==============================
display(Markdown("- Méthode 2 : méthode pas-à-pas"))
# On va calculer la solution générale, puis la solution particulière en prenant en compte les conditions initiales
solgen = sym.dsolve( [edo1,edo2], [y(t),z(t)] )
display(solgen)
# Étape 2 : calcul de la constante d'intégration en prenant en compte les conditions initiales :
cond_init1 = sym.Eq( y0, solgen[0].rhs.subs(t,t0) )
cond_init2 = sym.Eq( yp0, solgen[1].rhs.subs(t,t0) )
display(cond_init1)
display(cond_init2)
consts = sym.solve( [cond_init1,cond_init2] , dict=True)[0]
display(consts)
# Étape 3 : calcul de la solution particulière :
solpar = [sol.subs(consts) for sol in solgen]
display(solpar)\(\displaystyle \frac{d}{d t} y{\left(t \right)} = z{\left(t \right)}\)
\(\displaystyle \frac{d}{d t} z{\left(t \right)} = - 2 y{\left(t \right)} - 2 z{\left(t \right)} + 2 \sin{\left(t \right)}\)
\(\displaystyle y{\left(0 \right)} = 1\)
\(\displaystyle z{\left(0 \right)} = 0\)
- Méthode 1 : méthode directe
\(\displaystyle \left[ y{\left(t \right)} = \frac{2 \sin^{3}{\left(t \right)}}{5} - \frac{4 \sin^{2}{\left(t \right)} \cos{\left(t \right)}}{5} + \frac{2 \sin{\left(t \right)} \cos^{2}{\left(t \right)}}{5} - \frac{4 \cos^{3}{\left(t \right)}}{5} + \frac{7 e^{- t} \sin{\left(t \right)}}{5} + \frac{9 e^{- t} \cos{\left(t \right)}}{5}, \ z{\left(t \right)} = \frac{4 \sin^{3}{\left(t \right)}}{5} + \frac{2 \sin^{2}{\left(t \right)} \cos{\left(t \right)}}{5} + \frac{4 \sin{\left(t \right)} \cos^{2}{\left(t \right)}}{5} + \frac{2 \cos^{3}{\left(t \right)}}{5} - \frac{16 e^{- t} \sin{\left(t \right)}}{5} - \frac{2 e^{- t} \cos{\left(t \right)}}{5}\right]\)
- Méthode 2 : méthode pas-à-pas
\(\displaystyle \left[ y{\left(t \right)} = - \left(\frac{C_{1}}{2} - \frac{C_{2}}{2}\right) e^{- t} \cos{\left(t \right)} + \left(\frac{C_{1}}{2} + \frac{C_{2}}{2}\right) e^{- t} \sin{\left(t \right)} + \frac{2 \sin^{3}{\left(t \right)}}{5} - \frac{4 \sin^{2}{\left(t \right)} \cos{\left(t \right)}}{5} + \frac{2 \sin{\left(t \right)} \cos^{2}{\left(t \right)}}{5} - \frac{4 \cos^{3}{\left(t \right)}}{5}, \ z{\left(t \right)} = C_{1} e^{- t} \cos{\left(t \right)} - C_{2} e^{- t} \sin{\left(t \right)} + \frac{4 \sin^{3}{\left(t \right)}}{5} + \frac{2 \sin^{2}{\left(t \right)} \cos{\left(t \right)}}{5} + \frac{4 \sin{\left(t \right)} \cos^{2}{\left(t \right)}}{5} + \frac{2 \cos^{3}{\left(t \right)}}{5}\right]\)
\(\displaystyle 1 = - \frac{C_{1}}{2} + \frac{C_{2}}{2} - \frac{4}{5}\)
\(\displaystyle 0 = C_{1} + \frac{2}{5}\)
\(\displaystyle \left\{ C_{1} : - \frac{2}{5}, \ C_{2} : \frac{16}{5}\right\}\)
\(\displaystyle \left[ y{\left(t \right)} = \frac{2 \sin^{3}{\left(t \right)}}{5} - \frac{4 \sin^{2}{\left(t \right)} \cos{\left(t \right)}}{5} + \frac{2 \sin{\left(t \right)} \cos^{2}{\left(t \right)}}{5} - \frac{4 \cos^{3}{\left(t \right)}}{5} + \frac{7 e^{- t} \sin{\left(t \right)}}{5} + \frac{9 e^{- t} \cos{\left(t \right)}}{5}, \ z{\left(t \right)} = \frac{4 \sin^{3}{\left(t \right)}}{5} + \frac{2 \sin^{2}{\left(t \right)} \cos{\left(t \right)}}{5} + \frac{4 \sin{\left(t \right)} \cos^{2}{\left(t \right)}}{5} + \frac{2 \cos^{3}{\left(t \right)}}{5} - \frac{16 e^{- t} \sin{\left(t \right)}}{5} - \frac{2 e^{- t} \cos{\left(t \right)}}{5}\right]\)
4 ✍ Exercices
4.1 🐍 Exercice (sympy)
Calculer la solution exacte du problème de Cauchy
\(\begin{cases} y'(t)=\dfrac{3}{2} y(t) \left( 1-\dfrac{y(t)}{6} \right),& t>0\\ y(0)=1. \end{cases}\)
- Utiliser la méthode directe pour calculer puis afficher l’unique solution.
- Que vaut \(\lim_{t\to\infty}y(t)\)?
- Bonus : si on utilise la méthode pas à pas, que remarquez-vous sur la solution générale ? Comment retrouver la solution directe ?
Remarque : ne pas écrire 3/2 mais sympy.Rational(3,2) pour éviter que ce terme soit évalué comme un flottant.
Code
\(\displaystyle \frac{d}{d t} y{\left(t \right)} = \frac{3 \cdot \left(1 - \frac{y{\left(t \right)}}{6}\right) y{\left(t \right)}}{2}\)
\(\displaystyle y{\left(0 \right)} = 1\)
Code
\(\displaystyle y{\left(t \right)} = \frac{6 \left(- e^{3 t} + 5 \sqrt{e^{3 t}}\right)}{25 - e^{3 t}}\)
Code
# Affichage
# =========
# Étape 1 : conversion de la solution en fonction numpy
func = sym.lambdify(t,solpar.rhs,'numpy')
# Étape 2 : plot
import matplotlib.pyplot as plt
import numpy as np
# plt.rcdefaults()
plt.rcParams.update({<span class="st">'font.size'</span>: <span class="dv">16</span>})
plt.figure(figsize=(10,7))
tt = np.linspace(0,10,101)
yy = func(tt)
plt.plot(tt,yy)
plt.grid();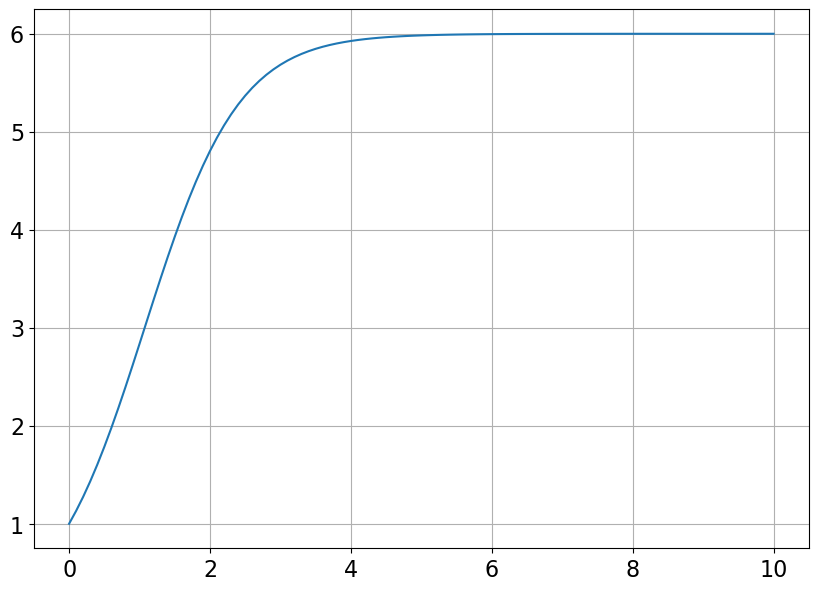
Code
\(\displaystyle \lim_{t \to \infty} y{\left(t \right)} = 6\)
Bonus : dans cet exemple, si on veut d’abord trouver la solution générale, on s’aperçoit qu’il y a deux expressions possibles. On doit alors choisir celle qui convient à notre condition initiale. Comme la solution du problème de Cauchy est unique, une seule des deux expressions est correcte.
Code
# Méthode pas-à-pas
# =================
# solgenLIST = sym.dsolve(edo,y(t))
# display(solgenLIST)
# On teste avec la première expression, si ça ne marche pas, on essaie avec la seconde
# =====================================================================================
# solgen = solgenLIST[0]
# display(solgen)
# equation = sym.Eq( y0, solgen.rhs.subs(t,t0))
# display(equation)
# consts = sym.solve( equation , dict=True)[0]
# display(consts)
# solpar = solgen.subs(consts)
# display(solpar)4.2 🐍 Exercice (sympy - système)
- Calculer la solution exacte du système
\( \begin{pmatrix} x(t)\\ y(t) \end{pmatrix}' = \begin{pmatrix} 0&1\\ -1&0 \end{pmatrix} \begin{pmatrix} x(t)\\ y(t) \end{pmatrix} \)
Pour \(x(0)=-1\) et \(y(0)=1\), afficher \(t\mapsto x\) et \(t\mapsto y\) dans un même graphe.
Afficher ensuite \(x\mapsto y\).
Calculer analytiquement \(E'(t)\) où \(t\mapsto E(t)\) est l’énergie mécanique du système définie par \( E(t)=\frac{x^2(t)}{2}+\frac{y^2(t)}{2}. \)
Bonus : transformer le système en une équation différentielle d’ordre 2 et résoudre le problème de Cauchy associé.
La première équation s’écrit
\( x'(t) = y(t) \)
et la deuxième
\( y'(t) = -x(t). \)
Code
%reset -f
%matplotlib inline
import sympy as sym
sym.init_printing()
t = sym.Symbol('t')
x = sym.Function('x')
y = sym.Function('y')
edo1 = sym.Eq( sym.diff(x(t),t) , y(t) )
edo2 = sym.Eq( sym.diff(y(t),t) , -x(t) )
display(edo1)
display(edo2)
t_0 = 0
x_0 = -1
y_0 = 1
display(sym.Eq(x(t_0),x_0))
display(sym.Eq(y(t_0),y_0))\(\displaystyle \frac{d}{d t} x{\left(t \right)} = y{\left(t \right)}\)
\(\displaystyle \frac{d}{d t} y{\left(t \right)} = - x{\left(t \right)}\)
\(\displaystyle x{\left(0 \right)} = -1\)
\(\displaystyle y{\left(0 \right)} = 1\)
Code
# Méthode directe
# ===============
solpar_1, solpar_2 = sym.dsolve( [edo1,edo2],
[x(t),y(t)],
ics={x(t_0):x_0, y(t_0):y_0} )
display(solpar_1)
display(solpar_2)
# Méthode pas-à-pas
# =================
# solgen = sym.dsolve([edo1,edo2],[x(t),y(t)])
# display(solgen)
# consts = sym.solve( [ sym.Eq( x_0, solgen[0].rhs.subs(t,t_0)) , sym.Eq( y_0, solgen[1].rhs.subs(t,t_0)) ] , dict=True)[0]
# display(consts)
# solpar_1 = solgen[0].subs(consts)
# solpar_2 = solgen[1].subs(consts)
# display(solpar_1)
# display(solpar_2)\(\displaystyle x{\left(t \right)} = \sin{\left(t \right)} - \cos{\left(t \right)}\)
\(\displaystyle y{\left(t \right)} = \sin{\left(t \right)} + \cos{\left(t \right)}\)
Code
# Conversion en fonctions numpy
# =============================
func_1 = sym.lambdify(t,solpar_1.rhs,'numpy')
func_2 = sym.lambdify(t,solpar_2.rhs,'numpy')
# Affichage
# =========
import matplotlib.pyplot as plt
import numpy as np
plt.rcParams.update({<span class="st">'font.size'</span>: <span class="dv">16</span>})
plt.figure(figsize=(17,7))
tt = np.linspace(0,30,101)
xx = func_1(tt)
yy = func_2(tt)
plt.subplot(1,2,1)
plt.plot(tt,xx,tt,yy)
plt.legend([r'$x(t)$',r'$y(t)$'])
plt.xlabel(r'$x$')
plt.grid()
plt.title('Solutions')
plt.subplot(1,2,2)
plt.plot(xx,yy)
# plt.axis('square')
plt.axis('equal')
plt.xlabel(r'$x$')
plt.ylabel(r'$y$')
plt.grid()
plt.title('Portrait de phase');
Code
# On calcule E et E' analytiquement
# ================================
# La fonction E(t) = x(t)^2/2 + y(t)^2/2
E = (solpar_1.rhs)**2/2+(solpar_2.rhs)**2/2
display(sym.Eq( sym.Symbol('E(t)') , E ))
# La dérivée de E par rapport à t
Ep = sym.diff(E,t).simplify()
display(sym.Eq( sym.Symbol("E'(t)") , Ep ))\(\displaystyle E(t) = \frac{\left(\sin{\left(t \right)} - \cos{\left(t \right)}\right)^{2}}{2} + \frac{\left(\sin{\left(t \right)} + \cos{\left(t \right)}\right)^{2}}{2}\)
\(\displaystyle E'(t) = 0\)
Transformation et résolution du système en une seule équation différentielle du deuxième ordre
On a \(x'(t)=y(t)\) et \(y'(t)=-x(t)\), on obtient alors \(x''(t)=y'(t)=-x(t)\).
De plus, \(x(0)=-1\) et \(x'(0)=y(0)=1\).
Code
import sympy as sym
sym.init_printing()
# Variables
t = sym.Symbol('t')
# Fonction inconnue
x = sym.Function('x')
# Équation différentielle
left = sym.diff(x(t),t,2)
right = -x(t)
edo = sym.Eq( left , right ) # l'équation différentielle
display(edo)
# Conditions initiales
t0 = 0
x0 = -1
xp0 = 1
display(sym.Eq(x(t0),x0))
display(sym.Eq(sym.diff(x(t),t).subs(t,t0),xp0))
# Méthode 1 : méthode directe
# ============================
solpar_x = sym.dsolve(edo,x(t), ics={x(t0):x0, sym.diff(x(t),t).subs(t,t0):xp0})
display(solpar_x)
solpar_y = sym.diff(solpar_x.rhs,t)
display( sym.Eq( y(t) , solpar_y ) )\(\displaystyle \frac{d^{2}}{d t^{2}} x{\left(t \right)} = - x{\left(t \right)}\)
\(\displaystyle x{\left(0 \right)} = -1\)
\(\displaystyle \left. \frac{d}{d t} x{\left(t \right)} \right|_{\substack{ t=0 }} = 1\)
\(\displaystyle x{\left(t \right)} = \sin{\left(t \right)} - \cos{\left(t \right)}\)
\(\displaystyle y{\left(t \right)} = \sin{\left(t \right)} + \cos{\left(t \right)}\)
