Devoir Maison 2020
1 Devoir Maison 2020
1.1 Exercice : implémentation et comparaison de schémas
Le déplacement \(x(t)\) d’un système oscillant composé d’une masse et d’un ressort, soumis à une force de frottement proportionnelle à la vitesse, est décrit par l’équation différentielle du second ordre \( x''(t)+ 5x'(t)+6x(t)=0, \) avec \(x(0) = 1\) et \(x'(0) = 0\), pour \(t \in [0, 5]\).
- Écrire le système sous forme matricielle. Calculer ensuite la solution exacte avec
sympy. Afficher \(t\mapsto x(t)\), \(t\mapsto x'(t)\) et \(x\mapsto x'(x)\). - Calculer la solution approchée obtenue par la méthode d’Euler Explicite avec \(301\) points. Afficher \(t\mapsto x(t)\), \(t\mapsto x'(t)\) et \(x\mapsto x'(x)\) en comparant solution exacte et solution approchée.
- Même exercice avec la méthode d’Euler Implicite.
- Même exercice avec la fonction
odeintdu modulescipy.
Q1
Écrire le système sous forme matricielle. Calculer ensuite la solution exacte avecsympy. Afficher \(t\mapsto x(t)\), \(t\mapsto x'(t)\) et \(x\mapsto x'(x)\).
Si on note \(y(t)=x(t)\) et \(z(t)=x'(t)\) on a \(y(0)=1\), \(z(0)=0\) et
\( \begin{cases} y'(t)=z(t),\\ z'(t)=-6y(t)-5z(t) \end{cases} \quad\text{i.e.}\quad \begin{pmatrix}y\\z\end{pmatrix}'(t) {}= \begin{pmatrix}0&1\\-6&-5\end{pmatrix} \begin{pmatrix}y\\z\end{pmatrix}(t) \)
Autrement dit :
\( \begin{aligned} \varphi \colon \mathbb{R}\times\mathbb{R}^2 &\to \mathbb{R}\\ \Big(t,(y,z)\Big) &\mapsto \begin{pmatrix}\varphi_1(t,(y,z)) = -z\\\varphi_2(t,(y,z))=-6y-5z\end{pmatrix} \end{aligned} \)
Pour simplifier les affichages, on définit une fonction affichage qui affiche les graphes de \(y_n\) et \(z_n\) en fonction de \(t_n\) et le portrait de phase \((y_n,z_n)\). Si une solution approchée est passé en argument, elle est aussi affichée pour comparaison.
Il suffira alors d’appeler cette fonction pour chaque schéma.
Code
# Discrétisation
# ==============
N = 300
tt = np.linspace(t0,tfinal,N+1)
# FONCTION UTILE
def affichage(tt, zz_exacte, zz=None, s=""):
# zz_exacte[:, 0] = y(t) = x(t)
# zz_exacte[:, 1] = z(t) = x'(t)
# zz[:, 0] = approx de zz_exacte[:, 0]
# zz[:, 1] = approx de zz_exacte[:, 1]
plt.figure(figsize=(17,7))
# Graphe de y(t) et z(t)
plt.subplot(1,2,1)
if zz is not None:
plt.plot(tt,zz[:, 0],'--',label=r'$u(t) \approx y(t)$',color="red")
plt.plot(tt,zz[:, 1],'--',label=r'$w(t) \approx z(t)$',color="blue")
plt.plot(tt,zz_exacte[:, 0],label=r"$y(t)=x(t)$",color="red")
plt.plot(tt,zz_exacte[:, 1],label=r"$z(t)=x'(t)$",color="blue")
plt.xlabel('t')
plt.legend()
plt.title(f'{</span>s<span class="sc">} - $y(t)$ et $z(t)$')
plt.grid()
# Diagramme de phase z(y)
plt.subplot(1,2,2)
if zz is not None:
plt.plot(zz[:, 0], zz[:, 1],'--',label='Approchée')
plt.plot(zz_exacte[:, 0], zz_exacte[:, 1],label='Exacte')
plt.xlabel('y')
plt.ylabel('z')
plt.legend()
if s!="":
plt.title(f'{</span>s<span class="sc">} - z(y)')
plt.grid()
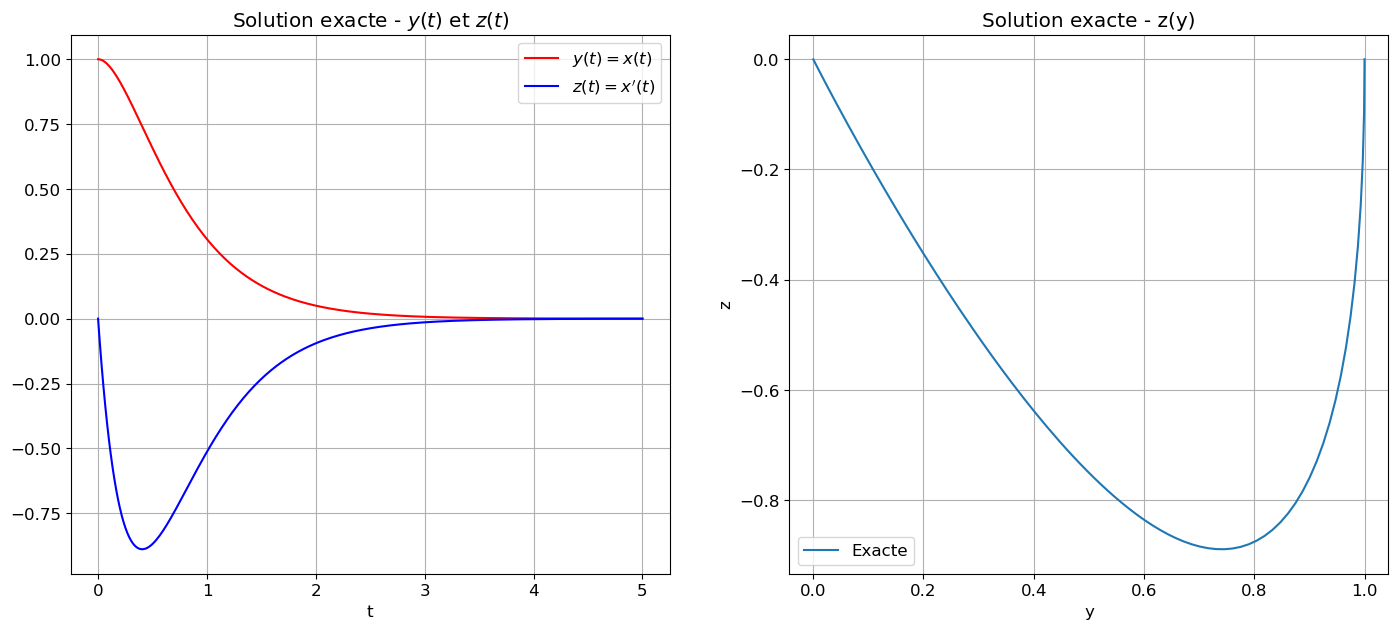
plt.axis('equal');La solution exacte est \(\begin{align*}
x(t)=y(t)&=3e^{-2t}−2e^{-3t},\\
x'(t)=z(t)&=-6e^{-2t}+6e^{-3t}.
\end{align*}\) Vérifions-le avec le module sympy:
Code
# Stratégie 1 : comme 1 EDO d'ordre 2
# =====================================
t = sym.Symbol('t')
x = sym.Function('x')(t)
t0 = 0
edo = sym.Eq( x.diff(t,t) + 5*x.diff(t) + 6*x , 0 )
sol = sym.dsolve(edo, x, ics={x.subs(t,t0):<span class="dv">1</span>, </span>
<span id="cb4-8"><a href="#cb4-8"></a> x.diff(t).subs(t,t0):<span class="dv">0</span>})
display(sol)
func_1 = sym.lambdify(t,sol.rhs,'numpy')
func_2 = sym.lambdify(t,sol.rhs.diff(t),'numpy')
# Stratégie 2 : comme 2 EDO d'ordre 1
# =====================================
# t = sym.Symbol('t')
# y = sym.Function('y')
# z = sym.Function('z')
# t0 = 0
# y0 = zz0[0]
# z0 = zz0[1]
# phi1 = lambda t,y,z : phi(t,[y,z])[0]
# phi2 = lambda t,y,z : phi(t,[y,z])[1]
# edo1 = sym.Eq( sym.diff(y(t),t) , phi1(t,y(t),z(t)) )
# edo2 = sym.Eq( sym.diff(z(t),t) , phi2(t,y(t),z(t)) )
# display(edo1)
# display(edo2)
# solpar_1, solpar_2 = sym.dsolve([edo1,edo2],
# [y(t),z(t)],
# ics={y(t0):y0, z(t0):z0})
# display(solpar_1)
# display(solpar_2)
# func_1 = sym.lambdify(t,solpar_1.rhs,'numpy')
# func_2 = sym.lambdify(t,solpar_2.rhs,'numpy')
# EVALUATION ET AFFICHAGE
y_vec = func_1(tt)
z_vec = func_2(tt)
zz_exacte = np.array([y_vec,z_vec]).T
affichage(tt,zz_exacte,s="Solution exacte")\(\displaystyle x{\left(t \right)} = \left(3 - 2 e^{- t}\right) e^{- 2 t}\)
Q2
Calculer la solution approchée obtenue par la méthode d’Euler Progressif avec \(301\) points. Afficher \(t\mapsto x(t)\), \(t\mapsto x'(t)\) et \(x\mapsto x'(x)\) en comparant solution exacte et solution approchée.
On notera \(u_n\approx y_n=x(t_n)\) et \(w_n\approx z(t_n)=x'(t_n)\).
Euler explicite \( \begin{cases} u_0=1,\\ w_0=0,\\ u_{n+1}=u_n+h\varphi_1(t_n,u_n,w_n),\\ w_{n+1}=w_n+h\varphi_2(t_n,u_n,w_n). \end{cases} \)
Code
def EE(phi,tt,zz0):
nb_eq = len(zz0) # nombre d'équations
N = len(tt)-1 # N+1 points, donc N intervalles
zz = np.zeros((N+1,nb_eq)) # colonnes = variables, lignes = temps
zz[0] = zz0
h = tt[1]-tt[0]
for n in range(N):
zz[n+1] = zz[n]+h*phi(tt[n],zz[n])
return zz
# Version qui retourne un tableau 1D si zz0 est scalaire
# def EE(phi, tt, zz0):
# zz0 = np.atleast_1d(zz0) # Convertir zz0 en tableau (même si scalaire)
# nb_eq = len(zz0) # Nombre d'équations
# N = len(tt) - 1 # N+1 points, donc N intervalles
# zz = np.zeros((N + 1, nb_eq)) # Colonnes = variables, lignes = temps
# zz[0] = zz0
# h = tt[1] - tt[0]
# for n in range(N):
# zz[n + 1] = zz[n] + h * phi(tt[n], zz[n])
# if nb_eq == 1:
# return zz.flatten() # Retourner un tableau 1D si scalaire
# return zz
zz_ep = EE(phi,tt,zz0)
affichage(tt,zz_exacte,zz=zz_ep,s="Euler explicite");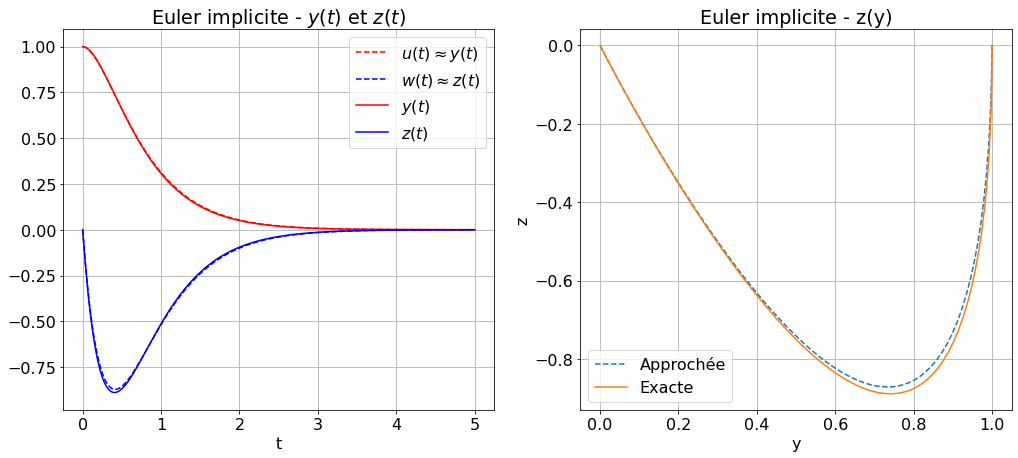
Q3
Calculer la solution approchée obtenue par la méthode d’Euler Regressif avec \(301\) points. Afficher \(t\mapsto x(t)\), \(t\mapsto x'(t)\) et \(x\mapsto x'(x)\) en comparant solution exacte et solution approchée.
Euler implicite \( \begin{cases} u_0=1,\\ w_0=0,\\ u_{n+1}=u_n+h\varphi_1(t_{n+1},u_{n+1},w_{n+1}),\\ w_{n+1}=w_n+h\varphi_2(t_{n+1},u_{n+1},w_{n+1}), \end{cases} \) qu’on peut rendre explicite par un calcul élementaire: \( w_{n+1} = w_n + h(-6u_{n+1}-5w_{n+1}) = w_n + h(-6(u_{n}+hw_{n+1})-5w_{n+1}) \quad\implies\quad (1+5h+6h^2)w_{n+1} = w_n-6hu_{n}\) ainsi \( \begin{cases} u_0=1,\\ w_0=0,\\ u_{n+1}=u_n+h\dfrac{w_n-6hu_{n}}{1+5h+6h^2},\\ w_{n+1}=\dfrac{w_n-6hu_{n}}{1+5h+6h^2}. \end{cases} \)
Code
# VERSION explicite
def EI(phi,tt,zz0):
h = tt[1]-tt[0]
uu, ww = np.zeros(len(tt)), np.zeros(len(tt))
uu[0], ww[0] = zz0
for n in range(len(tt)-1):
uu[n+1] = uu[n] + h*(ww[n]-6*h*uu[n])/(1+5*h+6*h**2)
ww[n+1] = (ww[n]-6*h*uu[n])/(1+5*h+6*h**2)
return np.array([uu,ww]).T
# VERSION AVEC fsolve
# from scipy.optimize import fsolve
# def EI(phi,tt,zz0):
# nb_eq = len(zz0) # nombre d'équations
# N = len(tt)-1 # N+1 points, donc N intervalles
# zz = np.zeros((N+1,nb_eq))
# zz[0] = zz0
# h = tt[1]-tt[0]
# for n in range(N):
# system = lambda z : z - zz[n] - h*phi(tt[n+1],z)
# zz[n+1] = fsolve( system , zz[n] )
# return zz
# Version qui retourne un tableau 1D si zz0 est scalaire
# def EI(phi, tt, zz0):
# zz0 = np.atleast_1d(zz0) # Convertir zz0 en tableau (même si scalaire)
# nb_eq = len(zz0) # Nombre d'équations
# N = len(tt) - 1 # N+1 points, donc N intervalles
# zz = np.zeros((N + 1, nb_eq))
# zz[0] = zz0
# h = tt[1] - tt[0]
# for n in range(N):
# system = lambda z: z - zz[n] - h * phi(tt[n + 1], z)
# zz[n + 1] = fsolve(system, zz[n])
# if nb_eq == 1:
# return zz.flatten() # Retourner un tableau 1D si scalaire
# return zz
zz_ei = EI(phi,tt,zz0)
affichage(tt,zz_exacte,zz=zz_ei,s="Euler implicite");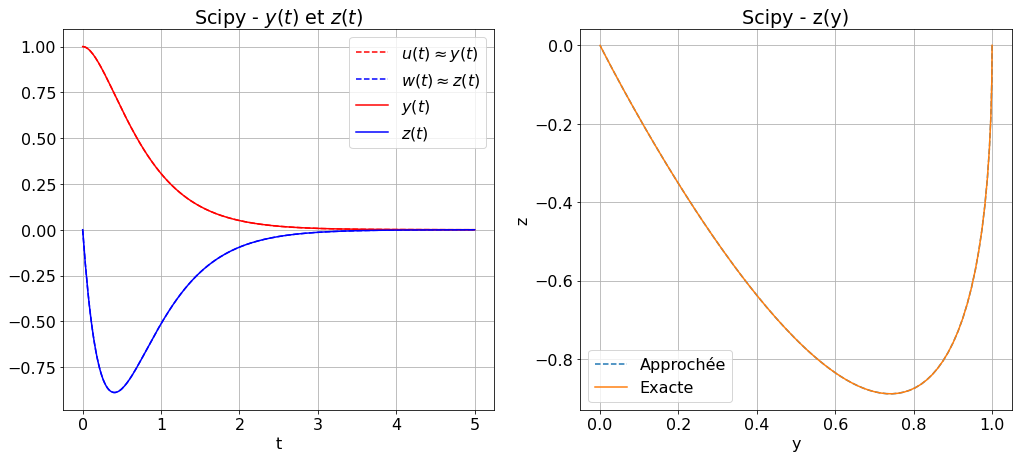
Q4
Calculer la solution approchée obtenue par la fonctionodeintdu modulescipy. Afficher \(t\mapsto x(t)\), \(t\mapsto x'(t)\) et \(x\mapsto x'(x)\) en comparant solution exacte et solution approchée.
Code
# OLD
from scipy.integrate import odeint
zz_odeint = odeint(phi,zz0,tt,tfirst=True)
affichage(tt,zz_exacte,zz=zz_odeint,s="odeint")
# NEW
from scipy.integrate import solve_ivp
zz_ivp = solve_ivp(phi,[t0,tfinal],zz0, t_eval=tt,
method='RK45'
# method='BDF'
).y.T
affichage(tt,zz_exacte,zz=zz_ivp,s="ivp")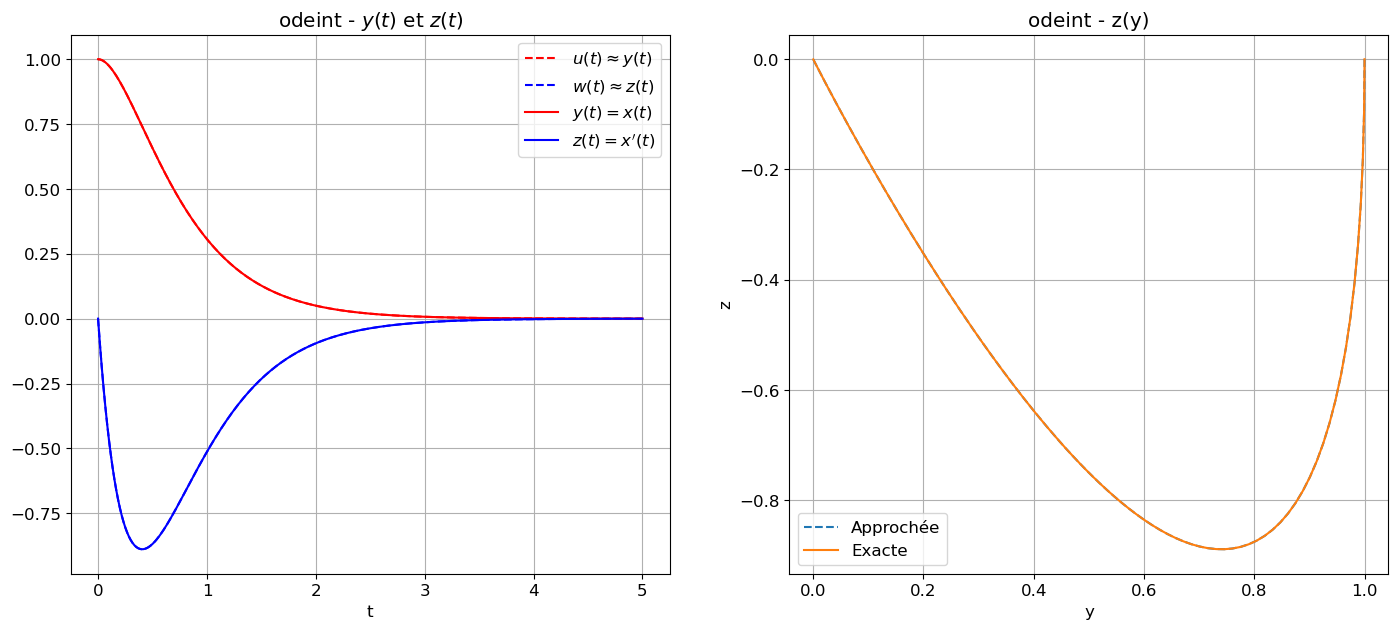
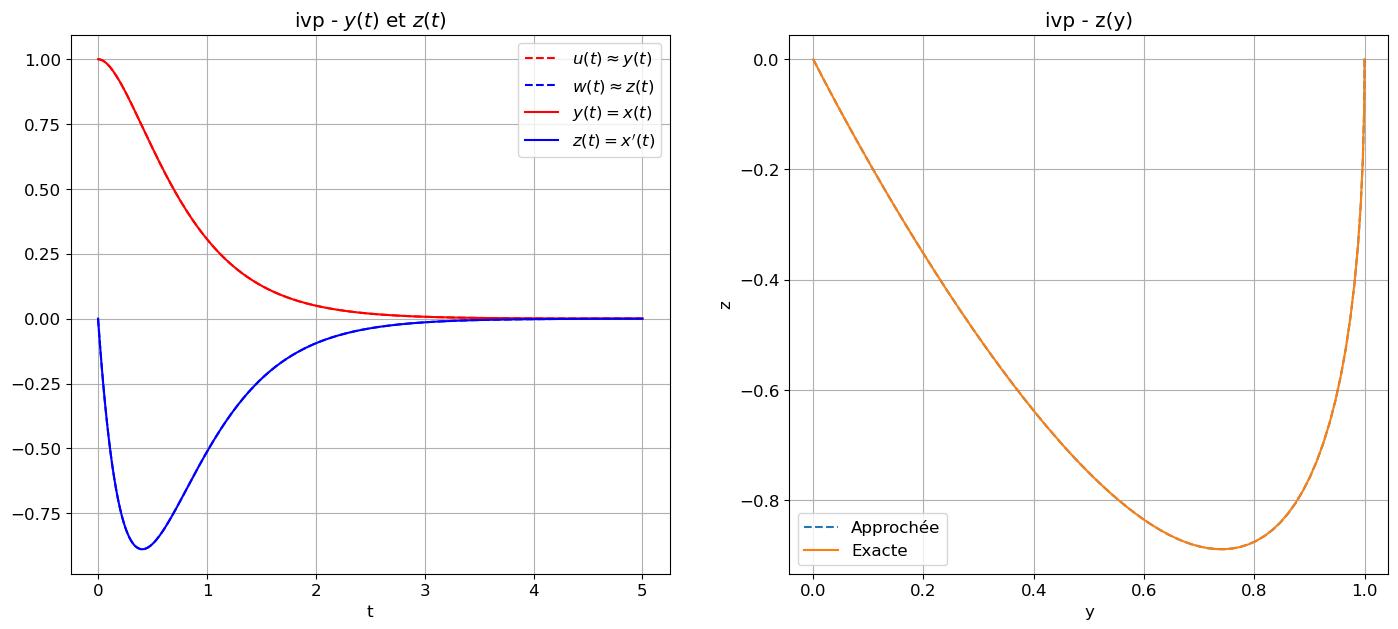
1.2 Exercice : étude d’un schéma RK semi-implicite à 2 étages
Soit le schéma de Runge-Kutta dont la matrice de Butcher est
\( \begin{array}{c|cc} \frac{1}{3} & \frac{1}{3} & 0\\ 1 & 1 & 0\\ \hline & \frac{3}{4} & \frac{1}{4} \end{array} \)
- Écrire le schéma sous la forme d’une suite définie par récurrence.
- Étudier théoriquement l’ordre de ce schéma.
- Étudier théoriquement la A-stabilité de ce schéma.
- Implémenter ce schéma et le tester sur le problème de Cauchy suivant avec \(N+1\) points et \(N=8\) : \( \begin{cases} y'(t)=-6y(t), &t\in[0;1]\\ y(0)=1 \end{cases} \)
Q5 Écrire le schéma sous la forme d’une suite définie par récurrence.
Le schéma associé à cette matrice est semi-implicite (\(K_0\) dépend de lui même) et permet de calculer \(u_{n+1}\) à partir de \(u_n\) par la formule de récurrence \(\begin{cases} u_0 = y_0 \\ K_0 = \varphi\left(t_n+\frac{h}{3},u_n+\frac{h}{3}K_0\right)\\ K_1 = \varphi\left(t_{n+1},u_n+hK_0\right)\\ u_{n+1} = u_n + \frac{h}{4}\left(3K_0+K_1\right) & n=0,1,\dots N-1 \end{cases}\)
Q6 Étudier théoriquement l’ordre du schéma.
Soit \(\omega\) l’ordre de la méthode.
C’est un schéma semi-implicite à \(2\) étages (\(s=2\)) donc \(\omega\le2s=4\)
Code
# =============================================================================
# Fonctions pour calculer les conditions de consistance pour un schéma RK.
#
# La fonction ordre_RK calcule les conditions pour les ordres 1, 2, 3 et 4 (même si théoriquement cela n'est pas possible)
# - affiche la matrice de Butcher
# - affiche les conditions de consistance obtenues pour chaque ordre par la fonction ordre_i
# - renvoie une liste d'équations pour une éventuelle résolution
#
# Chaque fonction ordre_i calcule les conditions pour être d'ordre i
# - peut afficher les conditions de consistance [actuellement en commentaire]
# - renvoie la liste d'équations
#
# =============================================================================
import sympy
sympy.init_printing()
from IPython.display import display, Math, Markdown
prlat = lambda *args : display(Math(''.join( sympy.latex(arg) for arg in args )))
def ordre_RK(s, type="implicite", A=None, b=None, c=None):
j = sympy.symbols('j')
if A is None:
if type == "implicite":
A = sympy.MatrixSymbol('a', s, s)
elif type=="semi-implicite":
A = sympy.Matrix(s, s, lambda i,j: sympy.Symbol('a{}{}'.format(i, j)) if i >= j else 0)
elif type=="explicite":
A = sympy.Matrix(s, s, lambda i,j: sympy.Symbol('a{}{}'.format(i, j)) if i > j else 0)
else:
A = sympy.Matrix(A)
if c is None:
c = sympy.symbols(f'c_0:{</span>s<span class="sc">}')
if b is None:
b = sympy.symbols(f'b_0:{</span>s<span class="sc">}')
display(Markdown("**Matrice de Butcher**"))
But = matrice_Butcher(s, A, b, c)
Eqs = []
display(Markdown(f"**On a {</span>s<span class="op">+</span><span class="dv">1</span><span class="sc">} conditions pour avoir consistance (= pour être d'ordre 1)**"))
Eq_1 = ordre_1(s, A, b, c, j)
Eqs.append(Eq_1)
display(*Eq_1)
display(Markdown("**On doit ajouter 1 condition pour être d'ordre 2**"))
Eq_2 = ordre_2(s, A, b, c, j)
Eqs.append([Eq_2])
display(Eq_2)
display(Markdown("**On doit ajouter 2 conditions pour être d'ordre 3**"))
Eq_3 = ordre_3(s, A, b, c, j)
Eqs.append(Eq_3)
display(*Eq_3)
display(Markdown("**On doit ajouter 4 conditions pour être d'ordre 4**"))
Eq_4 = ordre_4(s, A, b, c, j)
Eqs.append(Eq_4)
display(*Eq_4)
return Eqs
def matrice_Butcher(s, A, b, c):
But = sympy.Matrix(A)
But = But.col_insert(0, sympy.Matrix(c))
last = [sympy.Symbol(" ")]
last.extend(b)
But = But.row_insert(s,sympy.Matrix(last).T)
display(Math(sympy.latex(sympy.Matrix(But))))
return But
def ordre_1(s, A, b, c, j):
texte = r"\sum_{j=1}^s b_j =" + f"{</span><span class="bu">sum</span>(b)<span class="sc">.</span>simplify()<span class="sc">}"
texte += r"\text{ doit être égale à }1"
# display(Math(texte))
Eq_1 = [sympy.Eq( sum(b).simplify(), 1 )]
for i in range(s):
somma = sympy.summation(A[i,j],(j,0,s-1)).simplify()
texte = r'\sum_{j=1}^s a_{'</span><span class="op">+</span><span class="bu">str</span>(i)<span class="op">+</span><span class="vs">r'j}=' + sympy.latex( somma )
texte += r"\text{ doit être égale à }"+sympy.latex(c[i])
# display(Math( texte ))
Eq_1.append(sympy.Eq( somma, c[i] ))
return Eq_1
def ordre_2(s, A, b, c, j):
texte = r'\sum_{j=1}^s b_j c_j=' +sympy.latex(sum([b[i]*c[i] for i in range(s)]).simplify())
texte += r"\text{ doit être égale à }\frac{1}{2}"
# display(Math(texte))
Eq_2 = sympy.Eq( sum([b[i]*c[i] for i in range(s)]).simplify(), sympy.Rational(1,2) )
return Eq_2
def ordre_3(s, A, b, c, j):
texte = r'\sum_{j=1}^s b_j c_j^2='
texte += sympy.latex( sum([b[i]*c[i]**2 for i in range(s)]).simplify() )
texte += r"\text{ doit être égale à }\frac{1}{3}"
# display(Math(texte))
Eq_3_1 = sympy.Eq( sum([b[i]*c[i]**2 for i in range(s)]).simplify(), sympy.Rational(1,3) )
texte = r'\sum_{i,j=1}^s b_i a_{ij} c_j='
somma = sum([b[i]*A[i,j]*c[j] for j in range(s) for i in range(s)]).simplify()
texte = texte + sympy.latex(somma)
texte += r"\text{ doit être égale à }\frac{1}{6}"
# display(Math(texte))
Eq_3_2 = sympy.Eq( sum([b[i]*A[i,j]*c[j] for j in range(s) for i in range(s)]).simplify(), sympy.Rational(1,6) )
return [Eq_3_1, Eq_3_2]
def ordre_4(s, A, b, c, j):
texte = r'\sum_{j=1}^s b_j c_j^3='
texte += sympy.latex( sum([b[i]*c[i]**3 for i in range(s)]).simplify() )
texte += r"\text{ doit être égale à }\frac{1}{4}"
# display(Math(texte))
Eq_4_1 = sympy.Eq( sum([b[i]*c[i]**3 for i in range(s)]).simplify(), sympy.Rational(1,4) )
texte = r'\sum_{i,j=1}^s b_i c_i a_{ij} c_j='
somma = sum([b[i]*c[i]*A[i,j]*c[j] for j in range(s) for i in range(s)]).simplify()
texte = texte + sympy.latex(somma)
texte += r"\text{ doit être égale à }\frac{1}{8}"
# display(Math(texte))
Eq_4_2 = sympy.Eq( sum([b[i]*c[i]*A[i,j]*c[j] for j in range(s) for i in range(s)]).simplify(), sympy.Rational(1,8) )
texte = r'\sum_{i,j=1}^s b_i a_{ij} c_j^2='
somma = sum([b[i]*A[i,j]*c[j]**2 for j in range(s) for i in range(s)]).simplify()
texte = texte + sympy.latex(somma)
texte += r"\text{ doit être égale à }\frac{1}{12}"
# display(Math(texte))
Eq_4_3 = sympy.Eq( sum([b[i]*A[i,j]*c[j]**2 for j in range(s) for i in range(s)]).simplify(), sympy.Rational(1,12) )
texte = r'\sum_{i,j,k=1}^s b_i a_{ij} a_{jk} c_k='
somma = sum([b[i]*A[i,j]*A[j,k]*c[k] for k in range(s) for j in range(s) for i in range(s)]).simplify()
texte = texte + sympy.latex(somma)
texte += r"\text{ doit être égale à }\frac{1}{24}"
# display(Math(texte))
Eq_4_4 = sympy.Eq( sum([b[i]*A[i,j]*A[j,k]*c[k] for k in range(s) for j in range(s) for i in range(s)]).simplify(), sympy.Rational(1,24) )
return [Eq_4_1, Eq_4_2, Eq_4_3, Eq_4_4]
# =============================================================================
# Calcul des conditions de consistance pour un schéma RK
# On doit indiquer le nombre d'étages s et le type de schéma
# parmi implicite, semi-implicite ou explicite
# =============================================================================
s = 2
type = "semi-implicite" # implicite, semi-implicite, explicite
c = [sympy.Rational(1,3),1]
b = [sympy.Rational(3,4),sympy.Rational(1,4)]
A = [[sympy.Rational(1,3),0],[1,0]]
display(Markdown(f"### Conditions pour un schéma {</span><span class="bu">type</span><span class="sc">} avec s = {</span>s<span class="sc">} étages "))
Eqs = ordre_RK(s=s, type=type)
display(Markdown(f"### Pour notre exemple on trouve "))
Eqs = ordre_RK(s=s, type=type, A=A, b=b, c=c)1.2.1 Conditions pour un schéma semi-implicite avec s = 2 étages
Matrice de Butcher
\(\displaystyle \left[\begin{matrix}c_{0} & a_{00} & 0\\c_{1} & a_{10} & a_{11}\\ & b_{0} & b_{1}\end{matrix}\right]\)
On a 3 conditions pour avoir consistance (= pour être d’ordre 1)
\(\displaystyle b_{0} + b_{1} = 1\)
\(\displaystyle a_{00} = c_{0}\)
\(\displaystyle a_{10} + a_{11} = c_{1}\)
On doit ajouter 1 condition pour être d’ordre 2
\(\displaystyle b_{0} c_{0} + b_{1} c_{1} = \frac{1}{2}\)
On doit ajouter 2 conditions pour être d’ordre 3
\(\displaystyle b_{0} c_{0}^{2} + b_{1} c_{1}^{2} = \frac{1}{3}\)
\(\displaystyle a_{00} b_{0} c_{0} + a_{10} b_{1} c_{0} + a_{11} b_{1} c_{1} = \frac{1}{6}\)
On doit ajouter 4 conditions pour être d’ordre 4
\(\displaystyle b_{0} c_{0}^{3} + b_{1} c_{1}^{3} = \frac{1}{4}\)
\(\displaystyle a_{00} b_{0} c_{0}^{2} + a_{10} b_{1} c_{0} c_{1} + a_{11} b_{1} c_{1}^{2} = \frac{1}{8}\)
\(\displaystyle a_{00} b_{0} c_{0}^{2} + a_{10} b_{1} c_{0}^{2} + a_{11} b_{1} c_{1}^{2} = \frac{1}{12}\)
\(\displaystyle a_{00}^{2} b_{0} c_{0} + a_{00} a_{10} b_{1} c_{0} + a_{10} a_{11} b_{1} c_{0} + a_{11}^{2} b_{1} c_{1} = \frac{1}{24}\)
1.2.2 Pour notre exemple on trouve
Matrice de Butcher
\(\displaystyle \left[\begin{matrix}\frac{1}{3} & \frac{1}{3} & 0\\1 & 1 & 0\\ & \frac{3}{4} & \frac{1}{4}\end{matrix}\right]\)
On a 3 conditions pour avoir consistance (= pour être d’ordre 1)
\(\displaystyle \text{True}\)
\(\displaystyle \text{True}\)
\(\displaystyle \text{True}\)
On doit ajouter 1 condition pour être d’ordre 2
\(\displaystyle \text{True}\)
On doit ajouter 2 conditions pour être d’ordre 3
\(\displaystyle \text{True}\)
\(\displaystyle \text{True}\)
On doit ajouter 4 conditions pour être d’ordre 4
\(\displaystyle \text{False}\)
\(\displaystyle \text{False}\)
\(\displaystyle \text{False}\)
\(\displaystyle \text{False}\)
D’après ces résultats, le schéma est d’ordre \(3\).
Q7 Étudier théoriquement la A-stabilité du schéma.
Soit \(\beta>0\) un nombre réel positif et considérons le problème de Cauchy \(\begin{cases} y'(t)=-\beta y(t), &\text{pour }t>0,\\ y(0)=1. \end{cases}\) Sa solution est \(y(t)=e^{-\beta t}\) donc \(\lim_{t\to+\infty}y(t)=0.\)
Le schéma appliqué à ce problème de Cauchy s’écrit \(\begin{cases} u_0 = y_0 \\ K_0 = -\beta\left(u_n+\frac{h}{3}K_0\right)\\ K_1 = -\beta\left(u_n+hK_0\right)\\ u_{n+1} = u_n + \frac{h}{4}\left(3K_0+K_1\right) & n=0,1,\dots N-1 \end{cases}\)
L’équation \(K_0 = -\beta\left(u_n+\frac{h}{3}K_0\right)\) donne \(K_0=\frac{-3\beta}{\beta h+3}u_n\) ainsi \(u_{n+1} = u_n + \frac{h}{4}\left(3K_0+K_1\right) = u_n + \frac{h}{4}\left(3K_0-\beta u_n-\beta h K_0\right) = \left(1-\frac{\beta h}{4}\right)u_n + \frac{h(3-\beta h)}{4}K_0\) et enfin \( u_{n+1} = \left(1-\frac{\beta h}{4}\right)u_n + \frac{h(3-\beta h)}{4}K_0 = \left(1-\frac{\beta h}{4}\right)u_n + \frac{h(3-\beta h)}{4}\frac{-3\beta}{\beta h+3}u_n = \left(1-\frac{\beta h}{4} - \frac{3\beta h(3-\beta h)}{4(3 + \beta h)}\right)u_n % u_n + \frac{h}{4}\left( \frac{-9\beta}{\beta h+3}+\beta\frac{2\beta h-3}{\beta h+3}\right)u_ n = \frac{(\beta h)^2-4\beta h+6}{2(\beta h+3)}u_n \)
Vérifions ce calcul:
Code
# pour ne pas effacer l'affectation de "h", ici on vas l'appeler "dt" mais on affiche "h"
dt = sympy.Symbol('h')
u_np1 = sympy.Symbol('u_{n+1}')
beta = sympy.Symbol(r'\beta')
sympy.var('u_n,x')
K0 = sympy.solve(-x-beta*(u_n+dt/3*x),x)[0]
display(Math('K_0='+sympy.latex(K0)))
K1 = -beta*(u_n+dt*K0).factor()
display(Math('K_1='+sympy.latex(K1)))
u_np1 = (u_n+dt/4*(3*K0+K1)).factor()
display(Math('u_{n+1}='+sympy.latex(u_np1)))\(\displaystyle K_0=- \frac{3 \beta u_{n}}{\beta h + 3}\)
\(\displaystyle K_1=\frac{\beta u_{n} \left(2 \beta h - 3\right)}{\beta h + 3}\)
\(\displaystyle u_{n+1}=\frac{u_{n} \left(\beta^{2} h^{2} - 4 \beta h + 6\right)}{2 \left(\beta h + 3\right)}\)
On note \(x=\beta h\) et on étudie la fonction \(q\colon \mathbb{R}^+\to\mathbb{R}\) définie par \(q(x)=\dfrac{x^2-4x+6}{2(x+3)}=\dfrac{1}{2}\left(x-7+\dfrac{27}{x+3}\right)\). Le schéma est A-stable ssi \(|q(x)|<1\).
L’étude montre que la fonction \(q\) est continue et décroissante sur \([0,x_m]\) puis croissante sur \([x_m,+\infty[\) avec \(q(0)=1\) et \(0<q(x_m)<1\). Comme \(\lim_{x\to+\infty}q(x)=+\infty\), il existe un et un seul \(\hat x>x_m\) tel que \(q(\hat x)=1\). On trouve \(\hat x=6\).
D’après les calculs ci-dessous on conclut que le schéma est A-stable ssi \(h<\dfrac{6}{\beta}\).
Code
sympy.var('x',nonnegative=True)
q = (u_np1/u_n).subs(beta*dt,x)
display(Math('q(x)='+sympy.latex(q)))
display(Math('q(0)='+sympy.latex(q.subs(x,0))))
lim=sympy.Limit(q,x,sympy.oo)
display(Math(sympy.latex(lim)+'='+sympy.latex(lim.doit())))
print('On cherche les points stationnaires dans R^+')
dq=(q.diff(x)).factor()
display(Math("q'(x)="+sympy.latex(dq)))
print("Le signe de q' est le signe du numérateur qui est une parabole. On cherche où elle s'annulle pour x>0")
sol=sympy.solve(dq)
display(Math("q'(x)=0 \\iff x\\in"+sympy.latex(sol)))
minimum=sol[0]
display(Math("x="+sympy.latex(minimum)+"\\text{ est un minimum et}"))
qmin=q.subs(x,sol[0])
display(Math("q("+sympy.latex(minimum)+")="+sympy.latex(qmin)+"\\approx"+sympy.latex(sympy.N(qmin))))
print("Conclusion: q(x)>0 pour tout x>0. Vérifions ce calcul:")
print("q(x)>0")
display(sympy.solve(q>0))
print("On resout maintenant q(x)=1:")
display(sympy.solve(q-1))
print('On trouve q(0)=q(6)=1')
print("Conclusion: q(x)<1 pour x<6. Vérifions ce calcul:")
print("q(x)<1")
display(sympy.solve(q<1))
sympy.plot(q,1,-1,xlim=[-1,15],ylim=[-1.5,1.5]);\(\displaystyle q(x)=\frac{x^{2} - 4 x + 6}{2 x + 6}\)
\(\displaystyle q(0)=1\)
\(\displaystyle \lim_{x \to \infty}\left(\frac{x^{2} - 4 x + 6}{2 x + 6}\right)=\infty\)
On cherche les points stationnaires dans R^+
Le signe de q' est le signe du numérateur qui est une parabole. On cherche où elle s'annulle pour x>0
Conclusion: q(x)>0 pour tout x>0. Vérifions ce calcul:
q(x)>0
On resout maintenant q(x)=1:
On trouve q(0)=q(6)=1
Conclusion: q(x)<1 pour x<6. Vérifions ce calcul:
q(x)<1\(\displaystyle q'(x)=\frac{x^{2} + 6 x - 18}{2 \left(x + 3\right)^{2}}\)
\(\displaystyle q'(x)=0 \iff x\in\left[ -3 + 3 \sqrt{3}\right]\)
\(\displaystyle x=-3 + 3 \sqrt{3}\text{ est un minimum et}\)
\(\displaystyle q(-3 + 3 \sqrt{3})=\frac{\sqrt{3} \left(- 12 \sqrt{3} + \left(-3 + 3 \sqrt{3}\right)^{2} + 18\right)}{18}\approx0.196152422706632\)
\(\displaystyle \text{True}\)
\(\displaystyle \left[ 0, \ 6\right]\)
\(\displaystyle 0 < x \wedge x < 6\)
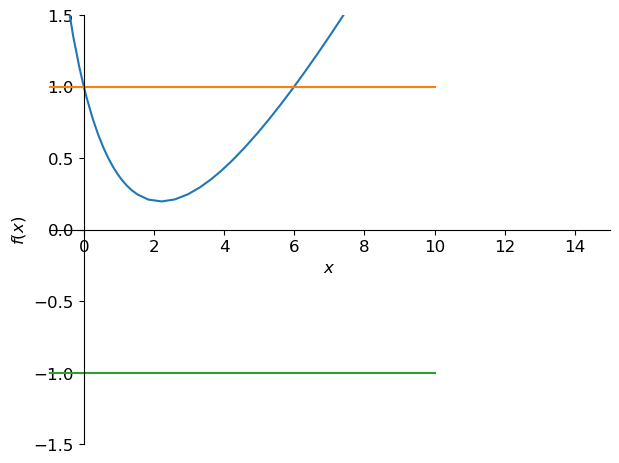
Q8 Implémenter le schéma et approcher la solution du problème de Cauchy suivant avec \(N+1\) points et \(N=8\). \( \begin{cases} y'(t)=-6y(t), &t\in[0;1]\\ y(0)=1 \end{cases} \)
Dans chaque point \(t_i\), il faut approcher \((K_0)_i\) en resolvant une équation. Si on utilise la fonction fsolve du module scipy.optimize, il faut initialiser fsolve avec une approximation de \((K_0)_i\). On choisira donc \(\varphi(t_i,u_i)\):
Code
from scipy.optimize import fsolve
# version implicite
def RK(phi,tt):
h = tt[1]-tt[0]
uu =np.zeros(len(tt))
uu[0] = y0
for n in range(len(tt)-1):
k0 = fsolve( lambda x : -x+phi( tt[n]+h/3, uu[n]+h/3*x ) , phi(tt[n],uu[n]) )[0]
k1 = phi( tt[n+1], uu[n]+h*k0 )
uu[n+1] = uu[n] + h/4*(3*k0+k1 )
return uu
# version explicite car phi = - beta h
# def RK(beta,tt):
# h = tt[1]-tt[0]
# x = beta*h
# q = lambda x : (x**2-4*x+6)/(2*x+6)
# uu = [y0*q(x)**n for n in range(len(tt))]
# return uu
t0, y0, tfinal = 0, 1, 3
beta = 6
sol_exacte = lambda t : np.exp(-beta*t)
phi = lambda t,y : -beta*y
print('A-stable ssi h <',6/beta)
plt.figure(figsize=(10,5))
N = 8
tt = np.linspace(t0,tfinal,N+1)
h = tt[1]-tt[0]
yy = sol_exacte(tt)
uu = RK(phi,tt) # version avec fsolve
# uu = RK(beta,tt) # version explicite
plt.plot(tt,yy,'b-',label=("Exacte"))
plt.plot(tt,uu,'ro',label=("RK"))
plt.title(r' $N$={}, $h$={}'.format(N,h))
plt.xlabel('$t$')
plt.ylabel('$u$')
plt.legend()
plt.grid(True)A-stable ssi h < 1.0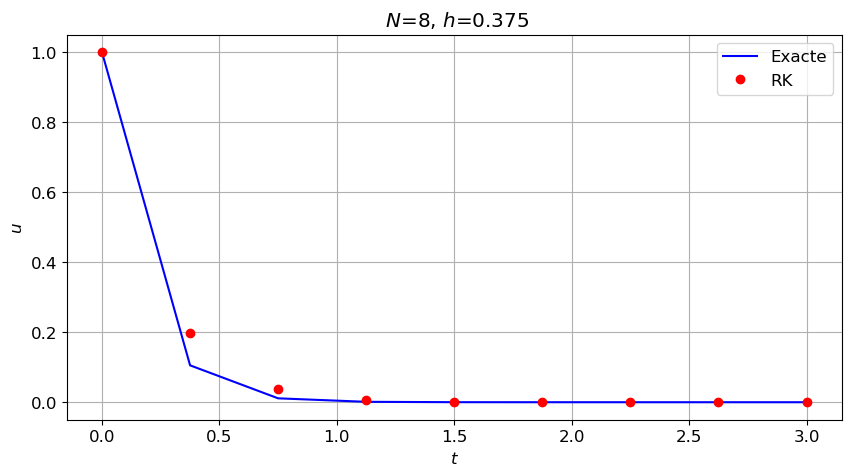
1.3 Exercice : étude d’un schéma Predictor-Corrector
Considérons les deux méthodes multi-pas linéaires suivantes :
\( \begin{aligned} u_{n+1}&=u_{n-3}+\frac{4h}{3}\left(2\varphi_{n}-\varphi_{n-1}+2\varphi_{n-2}\right)&\text{[P]} \\ u_{n+1}&=u_{n-1}+\frac{h}{3}\left(\varphi_{n+1}+4\varphi_{n}+\varphi_{n-1}\right)&\text{[C]} \end{aligned} \)
ayant noté \(\varphi_k\stackrel{\text{déf}}{=}\varphi(t_k,u_k)\).
- Étudier l’ordre de convergence théorique de chacune des deux méthodes.
- Écrire le schéma predictor-corrector associé à ces deux méthodes et en déterminer l’ordre de convergence théorique.
- Estimer empiriquement l’ordre de convergence des méthodes [P] et [C], ainsi que de la méthode Predictor-Corrector associée, en les appliquant au problème de Cauchy
\( \begin{cases} y'(t) = 1+\big(t-y(t)\big)^2, &\forall t \in I=[2,3],\\ y(2) = 1. \end{cases} \)
Code
%reset -f
import numpy as np
import matplotlib.pyplot as plt
plt.rcParams.update({<span class="st">'font.size'</span>: <span class="dv">12</span>})
import sympy as sym
sym.init_printing()
from IPython.display import display, Math, Markdown
def xi(i, q, aa=None, bb=None, bm1=None):
if aa is None:
aa = sym.symbols(f'a_0:{</span>q<span class="sc">}')
if bb is None:
bb = sym.symbols(f'b_0:{</span>q<span class="sc">}')
if bm1 is None:
bm1 = sym.symbols('b_{-1}')
p = len(aa)
sa = sum((-j)**i * aa[j] for j in range(p))
sb = bm1 + sum((-j)**(i-1) * bb[j] for j in range(1, p))
# ??? si j=0 et i=0, il calcule (-j)**i =1 et on a bien a_0 dans la somme
# mais si j=0 et i=1 il ne calcule pas b_0 et il faut l'ajouter à la main
if i == 1:
sb += bb[0]
return (sa) + (i * sb)
def afficahge_xi(q, aa, bb, bm1):
p = q-1
omega = q + 2 if q%2==0 else q + 1 # i = 0, ..., omega
display(Markdown(f"Pour une méthode à q={</span>q<span class="sc">} pas, on affiche $\\xi(i)$ pour i = 0, ..., {</span>q<span class="op">+</span><span class="dv">2</span><span class="sc">}"))
for i in range(q+3):
display(Markdown(f"$\\xi({</span>i<span class="sc">}) = {</span>sym<span class="sc">.</span>latex(xi(i, q, <span class="va">None</span>, <span class="va">None</span>, <span class="va">None</span>))<span class="sc">} = {</span>sym<span class="sc">.</span>latex(xi(i, q, aa, bb, bm1))<span class="sc">}$"))Q9 Étudier la méthode P.
[P] est une méthode à \(q=4\) pas explicite :
- \(p=3\)
- \(b_{-1}=0\)
- \(a_0=a_1=a_2=0\) et \(a_3=1\)
- \(b_0=\frac{8}{3}\), \(b_1=\frac{-4}{3}\), \(b_2=\frac{8}{3}\) et \(b_3=0\)
La méthode est explicite, donc son ordre de consistance maximal est \(q\). On vérifie qu’elle est effectivement consistante et son ordre de consistance est bien \(\omega=4\). En effet, \(\xi(0)=\xi(1)=\xi(2)=\xi(3)=\xi(4)=1\).
Vérifions ces calculs ci-dessous :
Code
Pour une méthode à q=3 pas, on affiche \(\xi(i)\) pour i = 0, …, 5
\(\xi(0) = a_{0} + a_{1} + a_{2} = 1\)
\(\xi(1) = - a_{1} - 2 a_{2} + b_{0} + b_{1} + b_{2} + b_{-1} = 1\)
\(\xi(2) = a_{1} + 4 a_{2} - 2 b_{1} - 4 b_{2} + 2 b_{-1} = 1\)
\(\xi(3) = - a_{1} - 8 a_{2} + 3 b_{1} + 12 b_{2} + 3 b_{-1} = 1\)
\(\xi(4) = a_{1} + 16 a_{2} - 4 b_{1} - 32 b_{2} + 4 b_{-1} = 1\)
\(\xi(5) = - a_{1} - 32 a_{2} + 5 b_{1} + 80 b_{2} + 5 b_{-1} = - \frac{109}{3}\)
Le premier polynôme caractéristique est
\( \varrho(r)=r^{p+1}-\sum_{j=0}^p a_jr^{p-j}=r^4-a_0r^3-a_1r^2-a_2r-a_3=r^4-1 \) dont les racines sont \( r_0=1,\ r_1=-1,\ r_2=i,\ r_3=-i \)
La méthode est zéro-stable ssi
\( \begin{cases} |r_j|\le1 \quad\text{pour tout }j=0,\dots,p \\ %|r_j|=1 \quad\implies \text{ $r_j$ a multiplicité 1, c'est-à-dire }\varrho'(r_j)\neq0, r_j\text{ a multiplicité}>1\quad\implies \quad |r_j|<1, \end{cases} \)
ce qui est bien vérifié.
Conclusion : la méthode est convergente car consistante et zéro-stable. Elle est d’ordre \(4\).
Q10 Étudier la méthode C.
[C] est une méthode à \(q=2\) pas implicite :
- \(p=1\)
- \(b_{-1}=\frac{1}{3}\)
- \(a_0=0\) et \(a_1=1\)
- \(b_0=\frac{4}{3}\) et \(b_1=\frac{1}{3}\)
La méthode est implicite avec un nombre pair de pas, donc son ordre de consistance maximal est \(q+2\). On vérifie qu’elle est effectivement consistante et son ordre de consistance est bien \(\omega=4\). En effet, \(\xi(0)=\xi(1)=\xi(2)=\xi(3)=\xi(4)=1\).
Vérifions ces calculs ci-dessous:
Code
Pour une méthode à q=2 pas, on affiche \(\xi(i)\) pour i = 0, …, 4
\(\xi(0) = a_{0} + a_{1} = 1\)
\(\xi(1) = - a_{1} + b_{0} + b_{1} + b_{-1} = 1\)
\(\xi(2) = a_{1} - 2 b_{1} + 2 b_{-1} = 1\)
\(\xi(3) = - a_{1} + 3 b_{1} + 3 b_{-1} = 1\)
\(\xi(4) = a_{1} - 4 b_{1} + 4 b_{-1} = 1\)
Le premier polynôme caractéristique est
\( \varrho(r)=r^{p+1}-\sum_{j=0}^p a_jr^{p-j}=r^2-a_0r-a_1=r^2-1 \)
dont les racines sont
\( r_0=1,\ r_1=-1 \)
La méthode est zéro-stable ssi
\( \begin{cases} |r_j|\le1 \quad\text{pour tout }j=0,\dots,p \\ r_j\text{ a multiplicité}>1\quad\implies \quad |r_j|<1, \end{cases} \)
ce qui est bien vérifié.
Conclusion : la méthode est convergente car consistante et zéro-stable. Elle est d’ordre \(4\).
Q11 Estimation empirique de l’ordre de convergence des méthodes P et C ainsi que de la méthode Predictor-Corrector associée aux deux méthodes P et C sur le problème de Cauchy
\( \begin{cases} y'(t) = 1+\big(t-y(t)\big)^2, &\forall t \in I=[2,3],\\ y(2) = 1. \end{cases} \)
Le schéma predictor-corrector est défini par
\( \begin{aligned} \tilde u_{n+1}&=u_{n-3}+\frac{4h}{3}\left(2\varphi_{n}-\varphi_{n-1}+2\varphi_{n-2}\right) \\ u_{n+1}&=u_{n-1}+\frac{h}{3}\left(\varphi(t_{n+1},\tilde u_{n+1})+4\varphi_{n}+\varphi_{n-1}\right) \end{aligned} \)
Ce schéma est d’ordre \(4\) car le prédictor est d’ordre \(4\), le corrector d’ordre \(4\) et l’on a
\( \omega_{[PC]} = \min \left\{ \omega_{[C]} , \omega_{[P]}+1 \right\} \)
On définit la solution exacte pour estimer les erreurs et on calcule la solution approchée pour différentes valeurs de \(N\) pour les trois schémas:
Code
t0 = 2
tfinal = 3
y0 = 1
phi = lambda t,y : 1+(t-y)**2
# Solution exacte
# ===============
t = sym.Symbol('t')
y = sym.Function('y')
edo = sym.Eq( sym.diff(y(t),t) , phi(t,y(t)) )
display(edo)
solpar = sym.dsolve( edo, y(t), ics={y(t0):y0})
display(solpar)
# Conversion en fonction numpy
# ============================
sol_exacte = sym.lambdify(t,solpar.rhs,'numpy')
# sol_exacte = lambda t : t+1/(1-t)
# Schémas
# =======
def predictor(phi, tt):
h = tt[1] - tt[0]
uu = np.zeros_like(tt)
uu[:4] = sol_exacte(tt[:4])
for n in range(3,len(tt) - 1):
k0 = phi(tt[n],uu[n])
k1 = phi(tt[n-1],uu[n-1])
k2 = phi(tt[n-2],uu[n-2])
uu[n+1] = uu[n-3] + 4*h/3*( 2*k0 - k1 + 2*k2 )
return uu
from scipy.optimize import fsolve
def corrector(phi, tt):
h = tt[1] - tt[0]
uu = np.zeros_like(tt)
uu[:2] = sol_exacte(tt[:2])
for n in range(1,len(tt) - 1):
k0 = phi(tt[n],uu[n])
k1 = phi(tt[n-1],uu[n-1])
temp = fsolve ( lambda x : -x + uu[n-1] + h/3*( phi(tt[n+1],x) + 4*k0 + k1 ), uu[n])
uu[n+1] = temp[0]
return uu
def PC(phi, tt):
h = tt[1] - tt[0]
uu = np.zeros_like(tt)
uu[:4] = sol_exacte(tt[:4])
for n in range(3,len(tt) - 1):
k0 = phi(tt[n],uu[n])
k1 = phi(tt[n-1],uu[n-1])
k2 = phi(tt[n-2],uu[n-2])
u_tilde = uu[n-3]+ 4*h/3*( 2*k0 - k1 + 2*k2 )
uu[n+1] = uu[n-1]+h/3* ( phi(tt[n+1],u_tilde) + 4*k0 + k1 )
return uu
# Calcul de l'ordre de convergence
# ===============================
H = []
err_p = []
err_c = []
err_pc = []
for N in range(10,160,20):
tt = np.linspace(t0, tfinal, N + 1)
h = tt[1] - tt[0]
yy = sol_exacte(tt)
uu_p = predictor(phi, tt)
uu_c = corrector(phi, tt)
uu_pc = PC(phi, tt)
H.append(h)
err_p.append(max([abs(uu_p[i] - yy[i]) for i in range(len(yy))]))
err_c.append(max([abs(uu_c[i] - yy[i]) for i in range(len(yy))]))
err_pc.append(max([abs(uu_pc[i] - yy[i]) for i in range(len(yy))]))
plt.figure(figsize=(8,5))
plt.plot(np.log(H), np.log(err_p), 'r-o', label=f'multi-pas [P], ordre = {</span>np<span class="sc">.</span>polyfit(np.log(H),np.log(err_p ), <span class="dv">1</span>)[<span class="dv">0</span>]<span class="sc">:g}')
plt.plot(np.log(H), np.log(err_c), 'b-o', label=f'multi-pas [C], ordre = {</span>np<span class="sc">.</span>polyfit(np.log(H),np.log(err_c ), <span class="dv">1</span>)[<span class="dv">0</span>]<span class="sc">:g}')
plt.plot(np.log(H), np.log(err_pc),'c-o', label=f'multi-pas [PC], ordre = {</span>np<span class="sc">.</span>polyfit(np.log(H),np.log(err_pc), <span class="dv">1</span>)[<span class="dv">0</span>]<span class="sc">:g}')
plt.xlabel(r'$\ln(h)$')
plt.ylabel(r'$\ln(e)$')
plt.legend(bbox_to_anchor=(1.04, 1), loc='upper left')
plt.grid(True);\(\displaystyle \frac{d}{d t} y{\left(t \right)} = \left(t - y{\left(t \right)}\right)^{2} + 1\)
\(\displaystyle y{\left(t \right)} = \frac{t^{2} - t - 1}{t - 1}\)
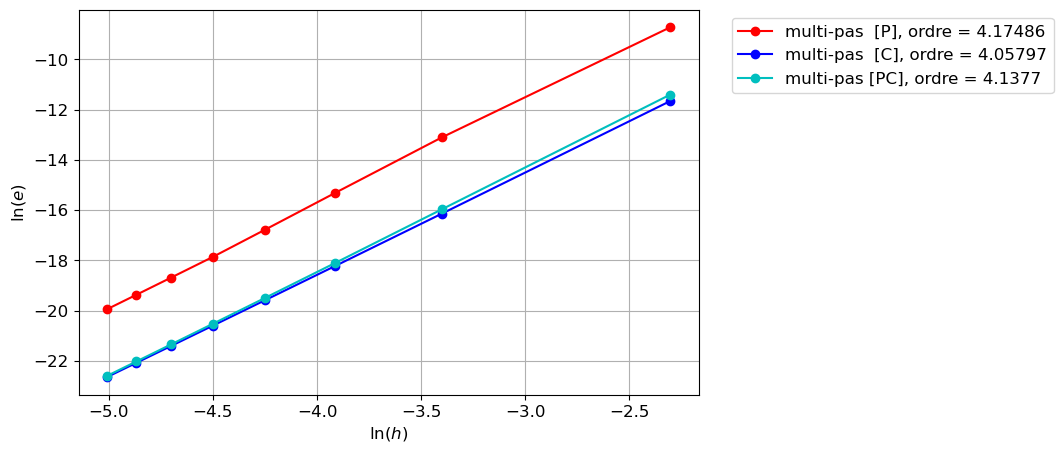
On a bien
- ordre du corrector \(\omega_{[C]}=4\)
- ordre du predictor \(\omega_{[P]}=4\)
et donc
- ordre du predictor-corrector \(\omega_{[PC]}=\min\{\omega_{[C]},\omega_{[P]}+1\}=4\)
