2021 CC v1 : le sujet comporte deux exercices indépendents.

1 2021 CC v1 : le sujet comporte deux exercices indépendents.

1.1 Exercice 1 : implémentation d’un schéma pour un système

Le modèle S.I.R. a été présenté pour la première fois par KERMACK & McKENDRICK à Londres et Cambridge en 1927 pour expliquer a posteriori l’évolution de l’épidémie de peste à Bombay en 1905-1906.

A chaque instant on décide de diviser la population en trois catégories (qu’on appelle « compartiments » dans le langage de l’épidémiologie): - les individus « Susceptibles » ou « Sains » (S) : ceux qui n’ont jamais eu la maladie et peuvent la contracter ; - les individus « Infectés » (I) : les malades, ce sont aussi les contagieux (c’est une hypothèse de ce modèle) ; - les individus « Rétablis » (R, comme « Recovered » en anglais) : ceux qui ont déjà eu la maladie et sont désormais immunisés contre cette maladie. Dans ce modèle on inclut dans ce groupe les personnes décédées (puisqu’elles ne peuvent plus contracter la maladie).

On travaillera avec des variables normalisées: leur valeur est comprise entre $0$ et $1$ et représente une fraction de la population totale (P).

Le modèle s’écrit $\begin{cases} S'(t)=-\beta S(t)I(t)\\ I'(t)=\beta S(t)I(t)-\nu I(t)\\ R'(t)=\nu I(t) \end{cases}$

Dans la suite, considérons les données initiales: - $S(0)=0.99$ - $I(0)=0.01$ - $R(0)=0$

Pour la rugéole on prendra - $\beta=0.8$ = taux de transmission (plus il est grand, plus la maladie est infectieuse) - $\nu=0.05$ = taux de rémission ou de décès du virus ( = 1 / (duréé moyenne de l’infection); plus $\nu$ est petit, plus le temps durant lequel le malade est contagieux est grand )

On simulera pour $t\in[0;90]$ jours

%reset -f
%matplotlib inline

from matplotlib.pylab import * # importe aussi numpy sans alias

beta = 0.8
nu   = 0.05  

# yy=[S,I,R]
phi0 = lambda S,I,R,t :  -beta*S*I
phi1 = lambda S,I,R,t :   beta*S*I-nu*I
phi2 = lambda S,I,R,t :   nu*I

S0=0.99
I0=1-S0
R0=0 

tt = linspace(0,90,91) # en jours
h = tt[1]-tt[0]

Q1
Soit $P(t)=S(t)+I(t)+R(t)$. Montrer que $P$ est un invariant.

$P'(t)=S'(t)+I'(t)+R'(t)=-\beta S(t)I(t)+\beta S(t)I(t)-\nu I(t)+\nu I(t)=0$.

Q2
Calculer la solution approchée obtenue par la méthode d’Euler Progressif avec $91$ points.
Afficher ensuite sur le même repère $t\mapsto S(t)$, $t\mapsto I(t)$, $t\mapsto R(t)$ et $t\mapsto P(t)$.

On notera $S_n\approx S(t_n)$, $I_n\approx I(t_n)$ et $R_n\approx R(t_n)$.

Euler explicite $\begin{cases} S_{n+1}=S_n+h\varphi_0(S_n,I_n,R_n,t_n),\\ I_{n+1}=I_n+h\varphi_1(S_n,I_n,R_n,t_n),\\ R_{n+1}=R_n+h\varphi_2(S_n,I_n,R_n,t_n). \end{cases}$

# S0, I0, R0, h variables globales
def euler_progressif(phi0,phi1,phi2,tt):
    SS = [S0]
    II = [I0]
    RR = [R0]
    for i in range(len(tt)-1):
        SS.append(SS[i]+h*phi0(SS[i],II[i],RR[i],tt[i]))
        II.append(II[i]+h*phi1(SS[i],II[i],RR[i],tt[i]))
        RR.append(RR[i]+h*phi2(SS[i],II[i],RR[i],tt[i]))
    return [SS,II,RR]

[SS_ep, II_ep, RR_ep] = euler_progressif(phi0,phi1,phi2,tt)

figure(figsize=(10,5))
PP_ep=[SS_ep[i]+II_ep[i]+RR_ep[i] for i in range(len(tt))]
plot(tt,SS_ep,'--',tt,II_ep,'.-',tt,RR_ep,':',tt,PP_ep)
xlabel('t')
legend(['S(t)','I(t)','R(t)','P(t)'])
title('Euler progressif') 
grid()
axis([tt[0],tt[-1],0,1.1]);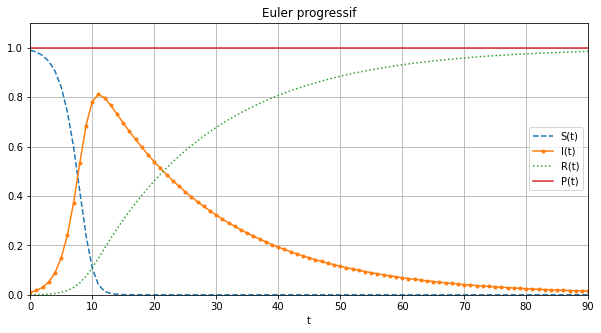

Q3
Calculer la solution approchée obtenue par la méthode d’Euler Régressif avec $91$ points.
Afficher ensuite sur le même repère $t\mapsto S(t)$, $t\mapsto I(t)$, $t\mapsto R(t)$ et $t\mapsto P(t)$.

On notera $S_n\approx S(t_n)$, $I_n\approx I(t_n)$ et $R_n\approx R(t_n)$.

Euler implicite $\begin{cases} S_{n+1}=S_n+h\varphi_0(S_{n+1},I_{n+1},R_{n+1},t_{n+1}),\\ I_{n+1}=I_n+h\varphi_1(S_{n+1},I_{n+1},R_{n+1},t_{n+1}),\\ R_{n+1}=R_n+h\varphi_2(S_{n+1},I_{n+1},R_{n+1},t_{n+1}). \end{cases}$

from scipy.optimize import fsolve
# S0, I0, R0, h variables globales
def euler_regressif(phi0,phi1,phi2,tt):
    SS = [S0]
    II = [I0]
    RR = [R0]
    for i in range(len(tt)-1):
        sys = lambda z : [ -z[0]+SS[i]+h*phi0(z[0],z[1],z[2],tt[i+1]) , -z[1]+II[i]+h*phi1(z[0],z[1],z[2],tt[i+1]) , -z[2]+RR[i]+h*phi2(z[0],z[1],z[2],tt[i+1]) ]
        Stemp,Itemp, Rtemp = fsolve( sys , (SS[i],II[i],RR[i]) ) 
        SS.append(Stemp)
        II.append(Itemp)
        RR.append(Rtemp)
    return [SS,II,RR]

[SS_er, II_er, RR_er] = euler_regressif(phi0,phi1,phi2,tt)

figure(figsize=(10,5))
PP_er=[SS_er[i]+II_er[i]+RR_er[i] for i in range(len(tt))]
plot(tt,SS_er,'--',tt,II_er,'.-',tt,RR_er,':',tt,PP_er)
xlabel('t')
legend(['S(t)','I(t)','R(t)','P(t)'])
title('Euler regressif') 
grid()
axis([tt[0],tt[-1],0,1.1]);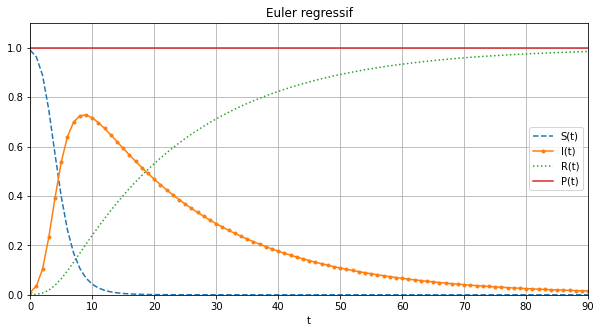

Q4
Calculer la solution approchée obtenue par la fonction odeint du module scipy.
Afficher ensuite sur le même repère $t\mapsto S(t)$, $t\mapsto I(t)$, $t\mapsto R(t)$ et $t\mapsto P(t)$.

from scipy.integrate import odeint

pphi = lambda yy,t : [ phi0(yy[0],yy[1],yy[2],t), phi1(yy[0],yy[1],yy[2],t), phi2(yy[0],yy[1],yy[2],t) ]
CI   = [S0,I0,R0]
sol  = odeint(pphi,CI,tt)

SS,II,RR = sol[:,0],sol[:,1],sol[:,2]

figure(figsize=(10,5))
PP = [SS[i]+II[i]+RR[i] for i in range(len(tt))]
plot(tt,SS,'--',tt,II,'.-',tt,RR,':',tt,PP)
xlabel('t')
legend(['S(t)','I(t)','R(t)','P(t)'])
title('Odeint') 
grid()
axis([tt[0],tt[-1],0,1.1]);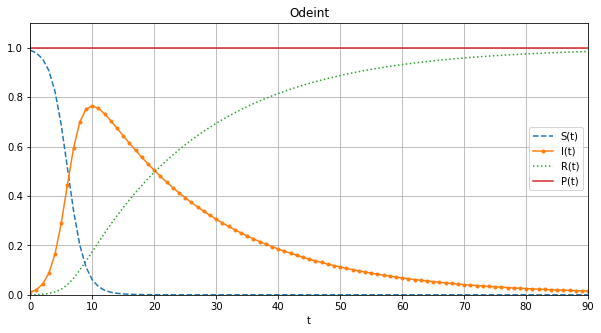

1.2 Exercice 2 : étude d’un schéma multipas

On notera $\varphi_k\stackrel{\text{déf}}{=}\varphi(t_k,u_k)$. Soit la méthode multipas $u_{n+1} =2\gamma u_{n} +\left(1-2\gamma \right)u_{n-1} +h\left(\gamma \varphi_{n+1} +\left(2-3\gamma \right)\varphi_{n}\right).$

Q5
Pour quelles valeurs de $$ est-elle consistante?

$p=1$: c’est une méthode à $q=p+1=2$ : - $a_0=2$ et $a_1=1-2$ - $b_0=2-3$ et $b_1=0$ - $b_{-1}=$

La méthode est implicite si $\gamma\neq0$.

• La méthode est consistante pour tout $\gamma$ car $\begin{cases} \displaystyle\sum_{j=0}^p a_j=a_0+a_1=2\gamma+(1-2\gamma)=1, \\ \displaystyle-\sum_{j=0}^p ja_j+\sum_{j=-1}^p b_j=-\big(0a_0+1a_1\big)+\big(b_{-1}+b_0+b_1\big)=-(1-2\gamma)+(\gamma+2-3\gamma)=1 \end{cases}$ Vérifions ces calculs ci-dessous:

import sympy as sym
sym.init_printing()

sym.var('gamma')
p=1
a0=2*gamma
a1=1-2*gamma
b0=2-3*gamma
b1=0
bm1=gamma

cond11=a0+a1
cond12=-(0*a0+1*a1)+(bm1+b0+b1)
display(cond11)
display(cond12.factor())
display(sym.solve([sym.Eq(cond11,1),sym.Eq(cond12,1)],gamma))

$\displaystyle 1$

$\displaystyle 1$

$\displaystyle \left[ \right]$

Q6
Pour quelles valeurs de $\gamma$ est-elle convergente?

• Le premier polynôme caractéristique est $\varrho(r)=r^{p+1}-\sum_{j=0}^p a_jr^{p-j}=r^2-a_0r-a_1 {}= r^2-2\gamma r+(2\gamma-1)$ dont les racines sont $r_0=1,\quad r_1=2\gamma-1.$

sym.var('r')
rho=r**2-a0*r-a1
display(sym.factor(rho))
sol=sym.solve(rho,r)
display(sol)

$\displaystyle \left(r - 1\right) \left(- 2 \gamma + r + 1\right)$

$\displaystyle \left[ 1, \ 2 \gamma - 1\right]$

• La méthode est zéro-stable ssi $\begin{cases} |r_j|\le1 \quad\text{pour tout }j=0,\dots,p \\ \varrho'(r_j)\neq0 \text{ si } |r_j|=1, \end{cases}$ donc ssi $0\le\gamma<1$.

cond=sym.solve([abs(c)<=1 for c in sol],gamma) 
print('La première condition impose')
display(cond) 

La première condition impose

$\displaystyle 0 \leq \gamma \wedge \gamma \leq 1$

• La méthode est convergente ssi elle est consistante et zéro-stable donc ssi $0\le\gamma<1$.

Q7
Quel ordre de convergente a-t-elle?

• La méthode est d’ordre au moins 2 car $\sum_{j=0}^p (-j)^{2}a_j+2\sum_{j=-1}^p (-j)^{1}b_j {}= \big(0^2a_0+1^2a_1\big)+2\big(-(-1)b_{-1}+0b_0+1b_1\big) {}= \big(1-2\gamma\big)+2\big(\gamma\big) {}= 1$

cond2=(0*a0+1*a1)+2*(-(-1)*bm1+0*b0+1*b1)
display(cond2.factor())
display(sym.solve(sym.Eq(cond2,1),gamma))

$\displaystyle 1$

$\displaystyle \left[ \right]$

• La méthode est d’ordre 3 ssi $\gamma=\frac{2}{5}$ car $\sum_{j=0}^p (-j)^{3}a_j+3\sum_{j=-1}^p (-j)^{2}b_j {}=-a_1+3\big(b_{-1}+b_1\big) {}=-(1-2\gamma)+3\big(\gamma\big) {}=5\gamma-1=1 \iff \gamma=\frac{2}{5}$

cond3=(0*a0-1*a1)+3*(1*bm1+0*b0+1*b1)
display(cond3.factor())
display(sym.solve(sym.Eq(cond3,1),gamma))

$\displaystyle 5 \gamma - 1$

$\displaystyle \left[ \frac{2}{5}\right]$

On conclut que - le schéma est convergent au moins d’ordre 2 pour tout $\gamma\in[0,1[$ - le schéma est convergent à l’ordre 3 pour $\gamma=\frac{2}{5}$ (et on peut montrer qu’il n’est pas d’ordre 4)

Q8
Pour deux valeurs différentes de $\gamma$ pour lesquelles le schéma est convergent (dont une qui donne l’ordre de convergence maximale), vérifier empiriquement l’ordre de convergence sur le problème de Cauchy $\begin{cases} y'(t) = y(t)(1-y(t)), &\forall t \in I=[0,1],\\ y(0) = 2, \end{cases}$ après avoir calculé la solution exacte.

• On définit la solution exacte (calculée en utilisant le module sympy) pour estimer les erreurs:

%reset -f
%matplotlib inline

from matplotlib.pylab import *

# variables globales
t0     = 0
tfinal = 1
y0     = 2

phi = lambda t,y : y*(1-y)

import sympy as sym
sym.init_printing()

t  = sym.Symbol('t')
y  = sym.Function('y')
edo= sym.Eq( sym.diff(y(t),t) , phi(t,y(t)) )
display(edo)
solgen = sym.dsolve(edo)
display(solgen)

consts = sym.solve( sym.Eq( y0, solgen.rhs.subs(t,t0)) , dict=True)[0]
display(consts)
solpar=solgen.subs(consts).simplify()
display(solpar)

sol_exacte = sym.lambdify(t,solpar.rhs,'numpy')

$\displaystyle \frac{d}{d t} y{\left(t \right)} = \left(1 - y{\left(t \right)}\right) y{\left(t \right)}$

$\displaystyle y{\left(t \right)} = \frac{1}{C_{1} e^{- t} + 1}$

$\displaystyle \left\{ C_{1} : - \frac{1}{2}\right\}$

$\displaystyle y{\left(t \right)} = \frac{2 e^{t}}{2 e^{t} - 1}$

On calcule la solution approchée pour différentes valeurs de $N$:

from scipy.optimize import fsolve

def multipas(phi, tt, gamma):
    h  = tt[1] - tt[0]
    uu = [y0]
    uu.append(sol_exacte(tt[1]))
    for i in range(1,len(tt) - 1):
        temp = fsolve( lambda x : -x+2*gamma*uu[i]+(1-2*gamma)*uu[i-1]+h*(gamma*phi(tt[i+1],x)+(2-3*gamma)*phi(tt[i],uu[i]))   ,uu[i])
        uu.append( temp )
    return uu

H = []
err_mp_2 = []
err_mp_3 = []
N = 10
for k in range(7):
    N+=20
    tt = linspace(t0, tfinal, N + 1)
    h = tt[1] - tt[0]
    yy = [sol_exacte(t) for t in tt]
    uu_mp_2 = multipas(phi, tt, 1/5)
    uu_mp_3 = multipas(phi, tt, 2/5)
    H.append(h)
    err_mp_2.append(max([abs(uu_mp_2[i] - yy[i]) for i in range(len(yy))]))
    err_mp_3.append(max([abs(uu_mp_3[i] - yy[i]) for i in range(len(yy))]))

print ('Multipas gamma=1/5 ordre=%1.2f' %(polyfit(log(H),log(err_mp_2), 1)[0]))
print ('Multipas gamma=2/5 ordre=%1.2f' %(polyfit(log(H),log(err_mp_3), 1)[0]))

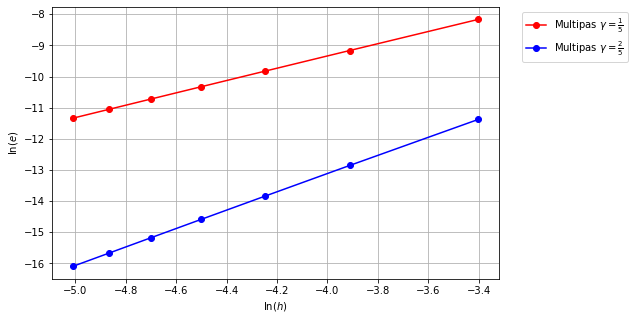
figure(figsize=(8,5))
plot(log(H), log(err_mp_2), 'r-o', label=r'Multipas $\gamma=\frac{1}{5}$')
plot(log(H), log(err_mp_3), 'b-o', label=r'Multipas $\gamma=\frac{2}{5}$')
xlabel('$\ln(h)$')
ylabel('$\ln(e)$')
legend(bbox_to_anchor=(1.04, 1), loc='upper left')
grid(True)
show()

Multipas gamma=1/5 ordre=1.97
Multipas gamma=2/5 ordre=2.94