2023 Contrôle Terminal session 2

Auteur·rice

Gloria FACCANONI

Date de publication

22 mars 2024

⏱ 2h30, deposer le notebook dans Moodle

1 EXERCICE 1 [4 points] : choix d’un schéma

Soit le problème de Cauchy $ \begin{cases} y'(t)=15y(t)+\frac{1-30t}{2\sqrt{t}}, & t\in[1;2]\\ y(1)=1+\varepsilon \end{cases}$

Calculer la solution exacte pour $\varepsilon\ge0$.
Soit $\varepsilon=0$. Approcher la solution du problème avec un des schémas classiques (EE, EI, EM, CN, Heun) qu’on choisira en fonction de la nature du problème de Cauchy (on justifiera ce choix). Afficher la solution exacte et la solution approchée sur le même répère avec $N = 100, 200, 300, 400, 500, 600$. Justifier le comportement de la solution approchée lorsque $N$ est petit.

💭 ne pas confondre sympy.sqrt (du module sympy pour le calcul de la solution exacte) et sqrt (du module numpy pour le calcul numérique).

On calcule la solution exacte. On remarque que c’est un problème de Cauchy numériquement mal posé: si $\varepsilon=0$ la fonction croît comme $\sqrt{t}$, si $\varepsilon>0$ comme une exponentielle. On doit donc choisir le schéma le plus précis parmi les schémas proposés, à savoir le schéma de Heun ou le schéma d’Euler Modifié ou de Crank-Nicolson qui sont d’ordre 2.

Code

%reset -f
%matplotlib inline

import sympy 
sympy.init_printing()

import numpy as np
import matplotlib.pyplot as plt
from scipy.optimize import fsolve

Code

# variables globales
t0     = 1
tfinal = 2

phi = lambda t,y: 15*y+(1-30*t)/(2*np.sqrt(t))


##############################################
# solution exacte
##############################################

phi_sym = lambda t,y: 15*y+(1-30*t)/(2*sympy.sqrt(t))
eps   = sympy.Symbol(r'\varepsilon', positive=True)
y0 = 1+eps

t   = sympy.Symbol('t')
y   = sympy.Function('y')
edo = sympy.Eq( sympy.diff(y(t),t) , phi_sym(t,y(t)) )
solgen = sympy.dsolve(edo,y(t))
display(solgen)
consts = sympy.solve( sympy.Eq( y0, solgen.rhs.subs(t,t0)) , dict=True)[0]
display(consts)
solpar = solgen.subs(consts).simplify()
display(solpar)


##############################################
# solution approchée
##############################################
y0 = 1
sol_exacte = sympy.lambdify(t,solpar.rhs.subs(eps,0),'numpy')

def EE(tt,phi,y0):
    h = tt[1]-tt[0]
    uu = np.zeros(len(tt))
    uu[0] = y0
    for i in range(N):
        uu[i+1] = uu[i]+h*phi(tt[i],uu[i])
    return uu

def EI(tt,phi,y0):
    h = tt[1]-tt[0]
    uu = np.zeros(len(tt))
    uu[0] = y0
    for i in range(N):
        temp = fsolve(lambda x: -x+uu[i]+h*phi(tt[i+1],x), uu[i])
        uu[i+1] = temp[0]
    return uu

def CN(tt,phi,y0):
    h = tt[1]-tt[0]
    uu = np.zeros(len(tt))
    uu[0] = y0
    for i in range(len(tt)-1):
        temp = fsolve(lambda x: -x+uu[i]+h/2*(phi(tt[i],uu[i])+phi(tt[i+1],x)), uu[i])
        uu[i+1] = temp[0]
    return uu

def Heun(tt,phi,y0):
    h = tt[1]-tt[0]
    uu = np.zeros(len(tt))
    uu[0] = y0
    for i in range(len(tt)-1):
        uu[i+1] = uu[i]+h/2*(phi(tt[i],uu[i])+phi(tt[i+1],uu[i]+h*phi(tt[i],uu[i])))
    return uu

def EM(tt,phi,y0):
    h = tt[1]-tt[0]
    uu = np.zeros(len(tt))
    uu[0] = y0
    for i in range(len(tt)-1):
        uu[i+1] = uu[i]+h*phi(tt[i]+h/2,uu[i]+h/2*phi(tt[i],uu[i])) 
    return uu


##############################################
# ordre
##############################################

for schema in ["CN","Heun","EM","EE","EI"]:

    plt.figure(figsize=(16,5))
    ax1 = plt.subplot(1,2,1)
    ax2 = plt.subplot(1,2,2)

    H = []
    err = []
    N = 100
    for k in range(6):
        N += 100
        tt = np.linspace(t0, tfinal, N + 1)
        H.append( tt[1] - tt[0] )
        yy = sol_exacte(tt)
        uu = eval(schema)(tt,phi,y0)
        err.append( np.linalg.norm(uu-yy,np.inf) )
        ax1.plot(tt,uu,label=f'Approchée avec N={</span>N<span class="sc">}')

    ax1.plot(tt,yy,label='Exacte')
    plt.xlabel('$t$')
    plt.ylabel('$y$')
    ax1.grid(True)
    ax1.legend()
    ax1.set_title(f'{</span>schema<span class="sc">}')

    ax2.plot( np.log(H), np.log(err), 'r-o')
    plt.xlabel('$\ln(h)$')
    plt.ylabel('$\ln(e)$')
    plt.title(f'Ordre = {</span>np<span class="sc">.</span>polyfit(np.log(H),np.log(err),<span class="dv">1</span>)[<span class="dv">0</span>]<span class="sc">:1.2f}')
    ax2.grid(True)

$\displaystyle y{\left(t \right)} = C_{1} e^{15 t} + \sqrt{t}$

$\displaystyle \left\{ C_{1} : \frac{\varepsilon}{e^{15}}\right\}$

$\displaystyle y{\left(t \right)} = \varepsilon e^{15 t - 15} + \sqrt{t}$

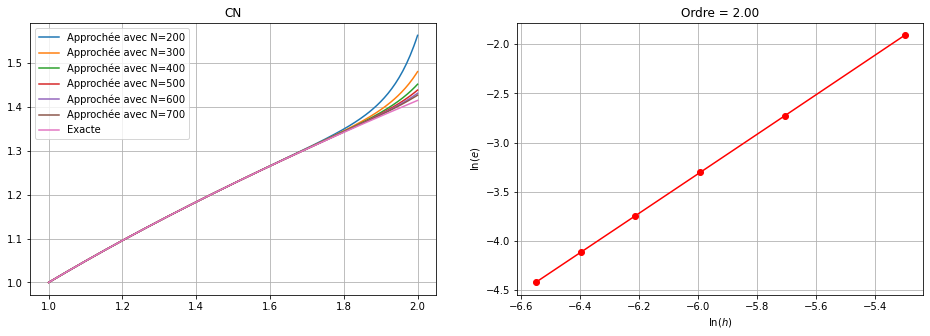
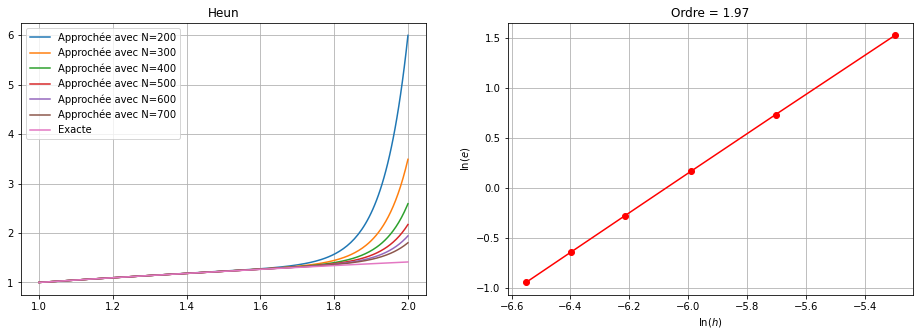
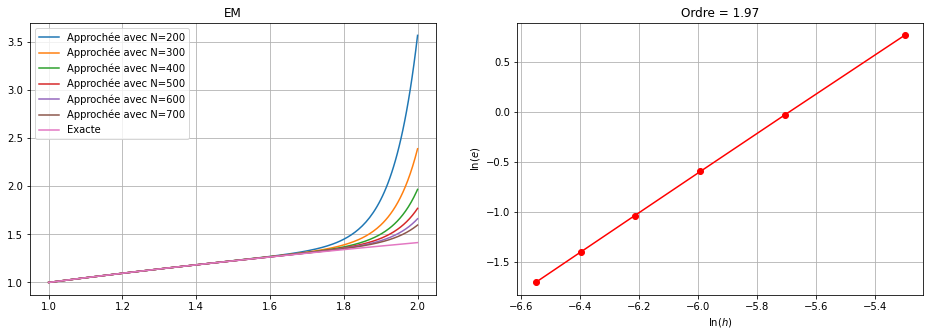
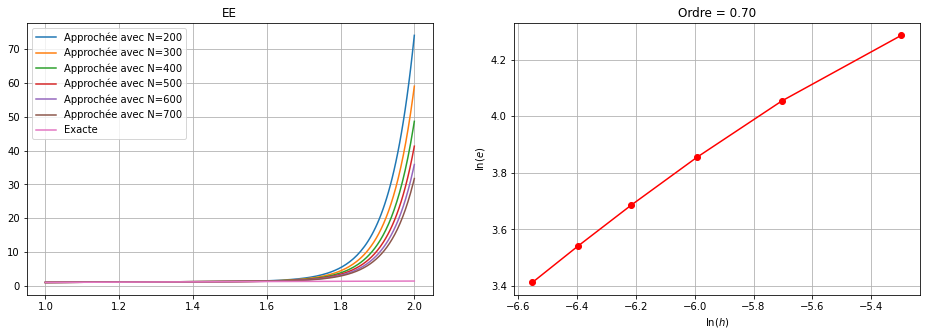
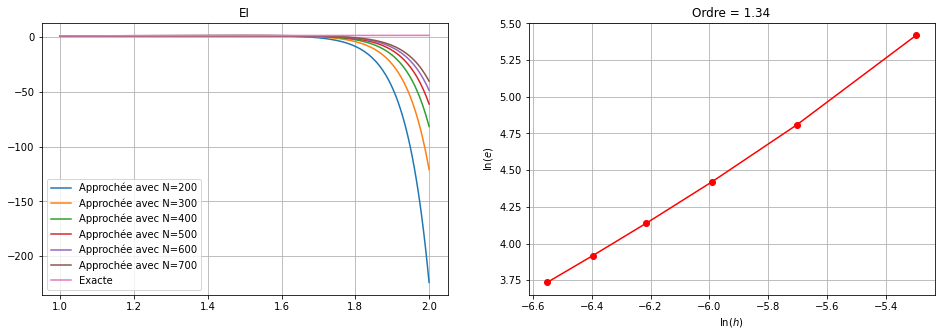
Comparons la valeurs de $y(2)$ obtenue avec les differents schémas:

Code

N = 600
tt = np.linspace(t0, tfinal, N + 1)
y_ex = sol_exacte(tt)[-1]
u_cn = CN(tt,phi,y0)[-1]
u_he = Heun(tt,phi,y0)[-1]
u_em = EM(tt,phi,y0)[-1]
u_ee = EE(tt,phi,y0)[-1]
u_ei = EI(tt,phi,y0)[-1]

from tabulate import tabulate
T = []
T.append(["y(2)", y_ex])
T.append(["CN", u_cn])
T.append(["EM", u_em])
T.append(["Heun", u_he])
T.append(["EE", u_ee])
T.append(["EI", u_ei])
tabulate(T,tablefmt="html",floatfmt=".2f")

y(2)	1.41
CN	1.43
EM	1.66
Heun	1.94
EE	35.89
EI	-48.81

2 Exercice 2 [16+1 points dont 8 sans coder] : étude d’un schéma Runge-Kutta

Considérons le schéma dont la matrice de Butcher est donnée ci-dessous: $ \begin{array}{c|ccc} 0 & 0 & 0 & 0 \\ \frac{1}{2} & \frac{1}{4} & \frac{1}{4}&0\\ 1 & \frac{1}{3} & \frac{1}{3} & \frac{1}{3} \\ \hline & \frac{1}{3} & \frac{1}{3} & \frac{1}{3} \end{array} $

Q1 [1 point] Écrire la suite définie par réccurence associée à ce schéma.

$\begin{cases} u_0 = y_0 \\ K_1 = \varphi\left(t_n,u_n\right)\\ K_2 = \varphi\left(t_n+\frac{h}{2},u_n+\frac{h}{4}\left(K_1+K_2\right)\right)\\ K_3 = \varphi\left(t_{n+1},u_n+\frac{h}{3}\left(K_1+K_2+K_3\right)\right)\\ u_{n+1} = u_n + \frac{h}{3}\left(K_1+K_2+K_3\right) & n=0,1,\dots N-1 \end{cases} $

Notons que $c_s=1$ et $a_{sj}=b_j$ pour tout $j=1,\dots,s$ ainsi $K_s=\varphi(t_{n+1},u_{n+1})$.

Q2 [5 points] Étudier empiriquement l’ordre de convergence sur le problème de Cauchy

$ \begin{cases} y'(t)=y(t)-(1+t^2)e^{-t}, & t\in[1;2]\\ y(1)=2/e \end{cases}$

💭 ne pas confondre sympy.exp (du module sympy pour le calcul de la solution exacte) et np.exp (du module numpy pour le calcul numérique).

Code

%reset -f
%matplotlib inline

import numpy as np
import matplotlib.pyplot as plt
from scipy.optimize import fsolve

import sympy 
sympy.init_printing()

Code

# variables globales
t0     = 1
tfinal = 2

phi = lambda t,y: y*(2*t-t**2-1)/(1+t**2)


##############################################
# solution exacte
##############################################
y0     = 2/sympy.E

t   = sympy.Symbol('t')
y   = sympy.Function('y')
edo = sympy.Eq( sympy.diff(y(t),t) , phi(t,y(t)) )
solgen = sympy.dsolve(edo)
display(solgen)
consts = sympy.solve( sympy.Eq( y0, solgen.rhs.subs(t,t0)) , dict=True)[0]
display(consts)
solpar = solgen.subs(consts).simplify()
display(solpar)

sol_exacte = sympy.lambdify(t,solpar.rhs,'numpy')

##############################################
# solution approchée
##############################################
y0     = 2/np.exp(1)

def RK(tt,phi,y0):
    h = tt[1]-tt[0]
    uu = np.zeros_like(tt)
    uu[0] = y0
    for i in range(len(tt)-1):
        sys = lambda X : [ -X[0]+phi( tt[i] , uu[i]                                 ) , 
                           -X[1]+phi( tt[i]+h/2 , uu[i]+h/4*(X[0]+X[1])             ), 
                           -X[2]+phi( tt[i+1]   ,uu[i]+h/3*(X[0]+X[1]+X[2])      )
                           ]
        K_start = phi(tt[i],uu[i])
        K1, K2, K3 = fsolve( sys , [K_start,K_start,K_start ] )
        uu[i+1] = uu[i]+h/3*(K1+K2+K3)
    return uu


##############################################
# ordre
##############################################
H = []
err = []
N = 10

plt.figure(figsize=(16,5))
ax1 = plt.subplot(1,2,1)
ax2 = plt.subplot(1,2,2)

for k in range(6):
    N += 20
    tt = np.linspace(t0, tfinal, N + 1)
    H.append( tt[1] - tt[0] )
    yy = sol_exacte(tt)
    uu = RK(tt,phi,y0)
    err.append( np.linalg.norm(uu-yy,np.inf) )
    ax1.plot(tt,uu,label=f'Approchée avec N={</span>N<span class="sc">}')

ax1.plot(tt,yy,label='Exacte')
plt.xlabel('$t$')
plt.ylabel('$y$')
ax1.grid(True)
ax1.legend()

ax2.plot( np.log(H), np.log(err), 'r-o')
plt.xlabel('$\ln(h)$')
plt.ylabel('$\ln(e)$')
plt.title(f'RK : ordre = {</span>np<span class="sc">.</span>polyfit(np.log(H),np.log(err),<span class="dv">1</span>)[<span class="dv">0</span>]<span class="sc">:1.2f}')
ax2.grid(True)

$\displaystyle y{\left(t \right)} = C_{1} \left(t^{2} + 1\right) e^{- t}$

$\displaystyle \left\{ C_{1} : 1\right\}$

$\displaystyle y{\left(t \right)} = \left(t^{2} + 1\right) e^{- t}$

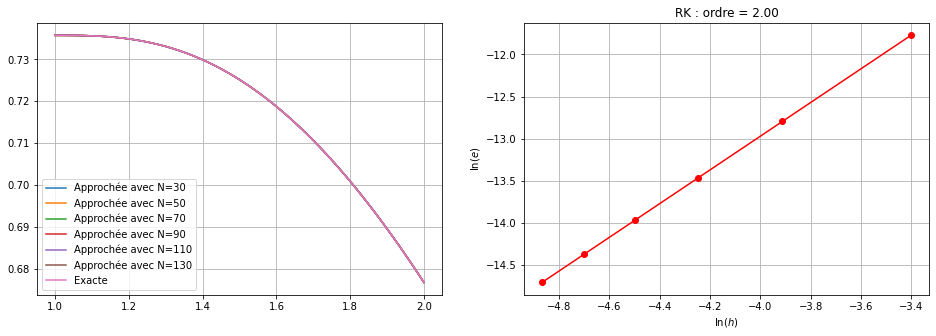
Q3 [3 points] Étudier théoriquement l’ordre du schéma.

Soit $\omega$ l’ordre de la méthode.

C’est un schéma (semi-)implicite à $3$ étages ($s=3$) donc $\omega\le2s=6$

Code

%reset -f
%matplotlib inline

import numpy as np
import matplotlib.pyplot as plt
from scipy.optimize import fsolve

import sympy 
sympy.init_printing()

from IPython.display import display, Math, Markdown
prlat= lambda *args: display(Math(''.join( sympy.latex(arg) for arg in args )))

Code

def ordre_RK(s, A=None, b=None, c=None):

    j = sympy.symbols('j')
    
    if A is None:
        A = sympy.MatrixSymbol('a', s, s)
    else:
        A = sympy.Matrix(A)
    if c is None:
        c = sympy.symbols(f'c_0:{</span>s<span class="sc">}')    
    if b is None:
        b = sympy.symbols(f'b_0:{</span>s<span class="sc">}')
    
    
    display(Markdown("**Matrice de Butcher**"))
    matrice_Butcher(s, A, b, c)
    
    display(Markdown(f"**On a {</span>s<span class="op">+</span><span class="dv">1</span><span class="sc">} conditions pour avoir consistance = pour être d'ordre 1**"))
    ordre_1(s, A, b, c, j)
    
    display(Markdown("**On doit ajouter 1 condition pour être d'ordre 2**"))
    ordre_2(s, A, b, c, j)

    display(Markdown("**On doit ajouter 2 conditions pour être d'ordre 3**"))
    ordre_3(s, A, b, c, j)    
    
    # display(Markdown("**On doit ajouter 4 conditions pour être d'ordre 4**"))
    # ordre_4(s, A, b, c, j)

    return None


def matrice_Butcher(s, A, b, c):
    But = sympy.Matrix(A)
    But = But.col_insert(0, sympy.Matrix(c))   
    last = [sympy.Symbol(" ")]
    last.extend(b)
    But = But.row_insert(s,sympy.Matrix(last).T)
    display(Math(sympy.latex(sympy.Matrix(But))))
    return None


def ordre_1(s, A, b, c, j):
    texte = "\sum_{j=1}^s b_j =" + f"{</span><span class="bu">sum</span>(b)<span class="sc">.</span>simplify()<span class="sc">}"
    texte += r"\text{ doit être égale à }1"
    display(Math(texte))
    for i in range(s):
        somma = sympy.summation(A[i,j],(j,0,s-1)).simplify()
        texte = r'\sum_{j=1}^s a_{'</span><span class="op">+</span><span class="bu">str</span>(i)<span class="op">+</span><span class="vs">r'j}=' + sympy.latex( somma )
        texte += r"\text{ doit être égale à }"+sympy.latex(c[i])
        display(Math( texte ))
    return None    


def ordre_2(s, A, b, c, j):
    texte = '\sum_{j=1}^s b_j c_j=' +sympy.latex(sum([b[i]*c[i] for i in range(s)]).simplify())
    texte += r"\text{ doit être égale à }\frac{1}{2}"
    display(Math(texte))
    return None


def ordre_3(s, A, b, c, j):
    texte = '\sum_{j=1}^s b_j c_j^2='
    texte += sympy.latex( sum([b[i]*c[i]**2 for i in range(s)]).simplify() )
    texte += r"\text{ doit être égale à }\frac{1}{3}"
    display(Math(texte))
    texte = r'\sum_{i,j=1}^s b_i a_{ij} c_j='
    somma = sum([b[i]*A[i,j]*c[j] for j in range(s) for i in range(s)]).simplify()
    texte = texte + sympy.latex(somma)
    texte += r"\text{ doit être égale à }\frac{1}{6}"
    display(Math(texte))
    return None


def ordre_4(s, A, b, c, j):
    texte = '\sum_{j=1}^s b_j c_j^3='
    texte += sympy.latex( sum([b[i]*c[i]**3 for i in range(s)]).simplify() )
    texte += r"\text{ doit être égale à }\frac{1}{4}"
    display(Math(texte))
    texte = r'\sum_{i,j=1}^s b_i c_i a_{ij} c_j='
    somma = sum([b[i]*c[i]*A[i,j]*c[j] for j in range(s) for i in range(s)]).simplify()
    texte = texte + sympy.latex(somma)
    texte += r"\text{ doit être égale à }\frac{1}{8}"
    display(Math(texte))
    texte = r'\sum_{i,j=1}^s b_i a_{ij} c_j^2='
    somma = sum([b[i]*A[i,j]*c[j]**2 for j in range(s) for i in range(s)]).simplify()
    texte = texte + sympy.latex(somma)
    texte += r"\text{ doit être égale à }\frac{1}{12}"
    display(Math(texte))
    texte = r'\sum_{i,j,k=1}^s b_i a_{ij} a_{jk} c_k='
    somma = sum([b[i]*A[i,j]*A[j,k]*c[k] for k in range(s) for j in range(s) for i in range(s)]).simplify()
    texte = texte + sympy.latex(somma)
    texte += r"\text{ doit être égale à }\frac{1}{24}"
    display(Math(texte))
    return None


# APPLICATION A NOTRE CAS
c = [0,sympy.Rational(1,2),1]
b = [sympy.Rational(1,3),sympy.Rational(1,3),sympy.Rational(1,3)]
A = [[0,0,0],[sympy.Rational(1,4),sympy.Rational(1,4),0],[sympy.Rational(1,3),sympy.Rational(1,3),sympy.Rational(1,3)]]
s = len(c)

display(Markdown(f"La méthode de Runge-Kutta est à {</span>s<span class="sc">} étages"))
ordre_RK(s,A,b,c)

La méthode de Runge-Kutta est à 3 étages

Matrice de Butcher

$\displaystyle \left[\begin{matrix}0 & 0 & 0 & 0\\\frac{1}{2} & \frac{1}{4} & \frac{1}{4} & 0\\1 & \frac{1}{3} & \frac{1}{3} & \frac{1}{3}\\ & \frac{1}{3} & \frac{1}{3} & \frac{1}{3}\end{matrix}\right]$

On a 4 conditions pour avoir consistance = pour être d’ordre 1

$\displaystyle \sum_{j=1}^s b_j =1\text{ doit être égale à }1$

$\displaystyle \sum_{j=1}^s a_{0j}=0\text{ doit être égale à }0$

$\displaystyle \sum_{j=1}^s a_{1j}=\frac{1}{2}\text{ doit être égale à }\frac{1}{2}$

$\displaystyle \sum_{j=1}^s a_{2j}=1\text{ doit être égale à }1$

On doit ajouter 1 condition pour être d’ordre 2

$\displaystyle \sum_{j=1}^s b_j c_j=\frac{1}{2}\text{ doit être égale à }\frac{1}{2}$

On doit ajouter 2 conditions pour être d’ordre 3

$\displaystyle \sum_{j=1}^s b_j c_j^2=\frac{5}{12}\text{ doit être égale à }\frac{1}{3}$

$\displaystyle \sum_{i,j=1}^s b_i a_{ij} c_j=\frac{5}{24}\text{ doit être égale à }\frac{1}{6}$

D’après ces résultats, le schéma est d’ordre $2$.

Q3 [4 points] Étudier théoriquement la A-stabilité du schéma.

La méthode appliquée à l’EDO $y'(t)=-\beta y(t)$ s’écrit: $\begin{cases} u_0 = y_0 \\ K_1 = -\beta\left(u_n\right)\\ K_2 = -\beta\left(u_n+\frac{h}{4}K_1+\frac{h}{4}K_2\right)\\ K_3 = -\beta\left(u_n+\frac{h}{3}K_1+\frac{h}{3}K_2+\frac{h}{3}K_3\right)\\ u_{n+1} = u_n + \frac{h}{3}\left(K_1+K_2+K_3\right) & n=0,1,\dots N-1 \end{cases}$

Code

sympy.var('u_n, h, β, K1, K2, K3')  
g = lambda y : -β*y
eq1 = sympy.Eq( K1 , g(u_n))
eq2 = sympy.Eq( K2 , g(u_n+h/4*K1+h/4*K2) )
eq3 = sympy.Eq( K3 , g(u_n+h/3*K1+h/3*K2+h/3*K3) )
sol = sympy.solve([eq1,eq2,eq3],[K1,K2,K3])
display(sol)
RHS = u_n+h/3*(K1+K2+K3)
RHS = RHS.subs(sol).simplify()
texte = 'u_{n+1}=' + sympy.latex(RHS)
display(Math(texte)) 
display(Markdown(r"Notons $x=hβ>0$. On trouve donc"))
x = sympy.Symbol('x',positive=True)
RHS = RHS.subs(h*β,x).simplify()
texte = 'u_{n+1}=' + sympy.latex(RHS)
display(Math(texte))

$\displaystyle \left\{ K_{1} : - u_{n} β, \ K_{2} : \frac{h u_{n} β^{2} - 4 u_{n} β}{h β + 4}, \ K_{3} : \frac{5 h u_{n} β^{2} - 12 u_{n} β}{h^{2} β^{2} + 7 h β + 12}\right\}$

$\displaystyle u_{n+1}=\frac{u_{n} \left(- 5 h β + 12\right)}{h^{2} β^{2} + 7 h β + 12}$

Notons $x=hβ>0$. On trouve donc

$\displaystyle u_{n+1}=\frac{u_{n} \left(12 - 5 x\right)}{x^{2} + 7 x + 12}$

Par induction on obtient $ u_{n}=\left(\frac{12-5x}{x^2+7x+12}\right)^nu_0. $ Par conséquent, $\lim\limits_{n\to+\infty}u_n=0$ si et seulement si $ \left|\frac{12-5x}{x^2+7x+12}\right|<1. $

Étudions la fonction $x\mapsto\frac{12-5x}{x^2+7x+12}$ pour $x>0$:

Code

q = sympy.apart(RHS/u_n)
prlat( r'q(x)=' , RHS/u_n  )
prlat( r'q(0)=' , q.subs(x,0) )

aaa = sympy.Limit(q,x,sympy.oo)
prlat( aaa, "=", aaa.doit()  )

prlat( r"q(x)=0", " ssi x =", sympy.solve(q)[0] )


dq = sympy.diff(q,x).apart()
prlat( r"q'(x)=" , dq )
prlat( r"q'(x)=0", " ssi x =", sympy.solve(dq)[0] )

q_numpy = sympy.lambdify(x,q,'numpy')
plt.figure(figsize=(10,5))
xx = np.linspace(0,50,100)
yy = q_numpy(xx)
plt.plot(xx,yy)
plt.plot([xx[0],xx[-1]],[-1,-1])
plt.plot([xx[0],xx[-1]],[1,1])
plt.grid();

$\displaystyle \mathtt{\text{q(x)=}}\frac{12 - 5 x}{x^{2} + 7 x + 12}$

$\displaystyle \mathtt{\text{q(0)=}}1$

$\displaystyle \lim_{x \to \infty}\left(- \frac{32}{x + 4} + \frac{27}{x + 3}\right)\mathtt{\text{=}}0$

$\displaystyle \mathtt{\text{q(x)=0}}\mathtt{\text{ ssi x =}}\frac{12}{5}$

$\displaystyle \mathtt{\text{q'(x)=}}\frac{32}{\left(x + 4\right)^{2}} - \frac{27}{\left(x + 3\right)^{2}}$

$\displaystyle \mathtt{\text{q'(x)=0}}\mathtt{\text{ ssi x =}}\frac{12}{5} + \frac{12 \sqrt{6}}{5}$

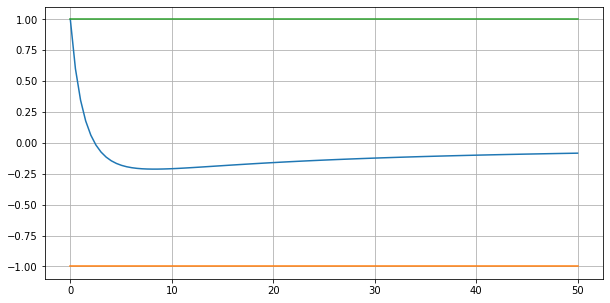
Elle est décroissante puis croissante. Elle atteint son minimum en $x_0=\frac{12}{5}(1+\sqrt{6})$ et $-1<q(x_0)<0$. Pour $x>x_0$ elle est croissante et $q(x)<0$.

La condition de stabilité est donc satisfaite pour tout $x$ donc pour tout $h$.
Notons que $q(x)>0$ ssi $x<\frac{12}{5}$.

Q4 [3 points] Considérons le problème de Cauchy $y'(t)=-50y(t)$ pour $t\in]0,1]$ et $y(0)=1$.
Vérifier empiriquement qu’avec $h>\frac{12}{250}$ le schéma est stable mais non monotone, tandis que pour $h<\frac{12}{250}$ le schéma est monotone.

Code

# variables globales
t0     = 0
tfinal = 1
y0     = 1
β      = 50

phi = lambda t,y: -β*y

##############################################
# solution exacte
##############################################
sol_exacte = lambda t : y0*np.exp(-β*t)

##############################################
# solution approchée
##############################################
def RK(tt,phi,y0):
    h = tt[1]-tt[0]
    uu = np.zeros_like(tt)
    uu[0] = y0
    for i in range(len(tt)-1):
        K1 = phi(tt[i],uu[i])
        sys = lambda X : [-X[0]+phi(tt[i]+h/2,uu[i]+h/4*(K1+X[0])) , -X[1]+phi(tt[i+1],uu[i]+h/3*(K1+X[0]+X[1]))]
        K2, K3 = fsolve( sys , [K1,K1] )
        uu[i+1] = uu[i]+h/3*(K1+K2+K3)
    return uu

##############################################
# ordre
##############################################

plt.figure(figsize=(16,5))

plt.subplot(1,2,1)
tt = np.arange(t0, tfinal, 12/250 + 0.01 )
h  = tt[1] - tt[0]
yy = np.array(sol_exacte(tt))
uu = RK(tt, phi, y0)
err = np.linalg.norm(uu-yy,np.inf)
plt.plot(tt,uu,label=f'Approchée avec h={</span>h<span class="sc">}')
plt.plot(tt,yy,label='Exacte')
plt.xlabel('$t$')
plt.ylabel('$y$')
plt.grid(True)
plt.legend();

plt.subplot(1,2,2)
tt = np.arange(t0, tfinal, 12/250 - 0.01 )
h  = tt[1] - tt[0]
yy = np.array(sol_exacte(tt))
uu = RK(tt, phi, y0)
err = np.linalg.norm(uu-yy,np.inf)
plt.plot(tt,uu,label=f'Approchée avec h={</span>h<span class="sc">}')
plt.plot(tt,yy,label='Exacte')
plt.xlabel('$t$')
plt.ylabel('$y$')
plt.grid(True)
plt.legend();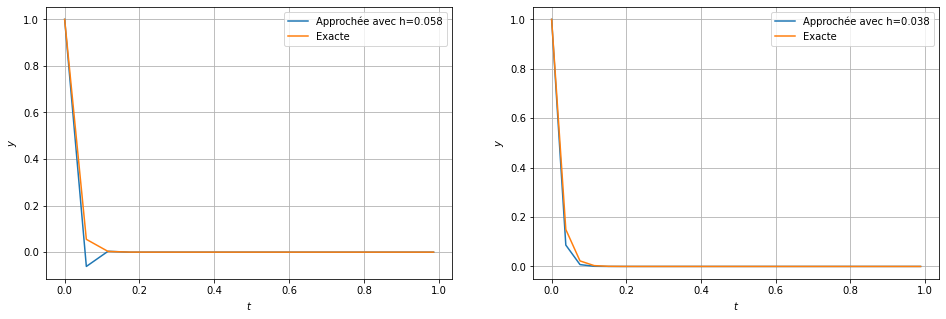

Q_Bonus [1 point] Montrer que ce schéma de type Runge-Kutta peut se réécrire sous la forme: $ \text{(CN-BDF$_2$)}\qquad \begin{cases} u_0=y_0,\\ \tilde u = u_n+\frac{h}{4}\left(\varphi(t_{n},u_{n})+\varphi\left(t_n+\frac{h}{2},\tilde u\right)\right) \\ u_{n+1}=\frac{1}{3}\left(-u_n+4\tilde u+h\varphi(t_{n+1},u_{n+1})\right) & n=0,1,2,\dots N-1. \end{cases}$ Autrement dit, $u_{n+1}$ est obtenu par une itération du schéma BDF_2 sur l’intervalle $[t_n;t_{n+1}]$. Ce schéma fait intervenir l’évaluation de $u$ en $t_n+\frac{h}{2}$. Cette valeur est alors approchée par la méthode de Crank-Nicolson sur le demi-interval $\left[t_n;t_{n}+\frac{h}{2}\right]$.

Les deux équations $\begin{cases} K_3 = \varphi\left(t_{n+1},u_n+\frac{h}{3}\left(K_1+K_2+K_3\right)\right)\\ u_{n+1} = u_n + \frac{h}{3}\left(K_1+K_2+K_3\right) \end{cases} $ impliquent $ K_3=\varphi\left(t_{n+1},u_{n+1}\right) $ ainsi, comme $K_1 = \varphi\left(t_n,u_n\right)$, on a $ u_{n+1} = u_n + \frac{h}{3}\left(\varphi\left(t_n,u_n\right)+K_2+\varphi\left(t_{n+1},u_{n+1}\right)\right). $

Si on note $ A = u_n+\frac{h}{4}\left(K_1+K_2\right), $ alors $ (A-u_n)\frac{4}{h}-K_1 = K_2 = \varphi\left(t_n+\frac{h}{2},u_n+\frac{h}{4}\left(K_1+K_2\right)\right)= \varphi\left(t_n+\frac{h}{2},A\right) $ soit encore $ A = u_n+\frac{h}{4}\left(K_1+\varphi\left(t_n+\frac{h}{2},A\right)\right) $ et enfin $ A = u_n+\frac{h}{4}\left(\varphi(t_n,u_n)+\varphi\left(t_n+\frac{h}{2},A\right)\right) $

On conclut alors que $ u_{n+1} = u_n + \frac{h}{3}\left( (A-u_n)\frac{4}{h}+\varphi\left(t_{n+1},u_{n+1}\right)\right) = \frac{1}{3}\left(3u_n+ 4(A-u_n)+h\varphi\left(t_{n+1},u_{n+1}\right)\right)= \frac{1}{3}\left( -u_n+ 4A+h\varphi\left(t_{n+1},u_{n+1}\right)\right) . $

Retour au sommet