2022 Contrôle Continu
- ⏱ 2H30
- ✍ Deposer votre fichier .ipynb sur Moodle (dépôt de devoir)
1 Exercice 1 : étude d’un schéma multipas
On notera \(\varphi_k\stackrel{\text{déf}}{=}\varphi(t_k,u_k)\).
Soit la méthode multipas
\( u_{n+1} = \alpha u_n + (1-\alpha) u_{n-1} +h\left(2\varphi_{n+1} -\frac{3\vartheta}{2}\varphi_{n}+\frac{\vartheta}{2} \varphi_{n-1}\right). \)
- Pour quelles valeurs des paramètres \(\alpha\) et \(\vartheta\) la méthode est zéro-stable ?
- Quel est l’ordre de convergence de la méthode?
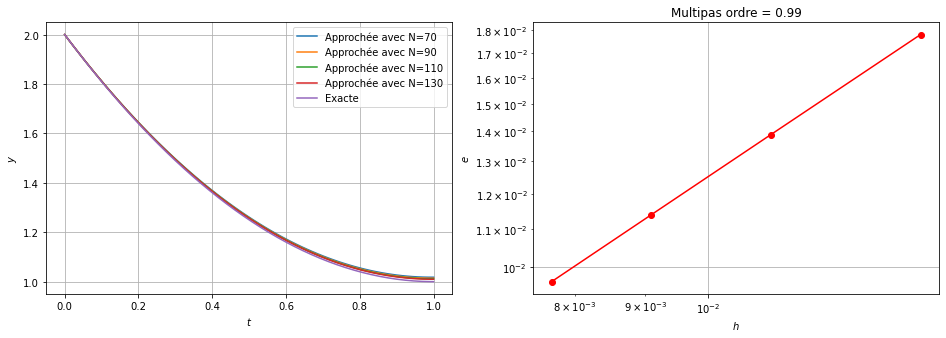
- Nous allons maintenant fixer \(\alpha\). Pour \(\vartheta\), choisir une valeur qui garantie la convergence. Vérifier empiriquement l’ordre de convergence sur le problème de Cauchy \(\begin{cases} y'(t) = t^2-y(t), &\forall t \in I=[0,1],\\ y(0) = 2. \end{cases} \)
Q1 [2 points]
Pour quelles valeurs des paramètres \(\alpha\) et \(\vartheta\) la méthode est zéro-stable?
Le premier polynôme caractéristique est
\( \varrho(r)=r^{p+1}-\sum_{j=0}^p a_jr^{p-j}=r^2-\alpha r+(\alpha-1)=(r-1)\big(r-(\alpha-1)\big) \)
dont les racines sont
\( r_0=1,\quad r_1=\alpha-1. \)
La méthode est donc zéro-stable ssi
\( \begin{cases} |r_j|\le1 \quad\text{pour tout }j=0,1 \\ \varrho'(r_j)\neq0 \text{ si } |r_j|=1 \end{cases} \)
donc ssi \(0\le\alpha<2\).
Q2 [3 points]
Quel est l’ordre de convergence de la méthode?
On rappelle qu’une méthode est convergente ssi elle est zéro-stable et consistante. Nous allons donc étudier la consistance (puis l’ordre de consistance = ordre de convergence) pour les seules valeurs de \(\alpha\) pour lesquelles on a la zéro-stabilité.
- On a \(p=1\): c’est une méthode à \(q=p+1=2\) pas.
- La méthode est implicite car \(b_{-1}=2\neq0\).
Pour que la méthode soit consistante il faut que \(\xi(0)=\xi(1)=1\).
De plus, la première barrière de Dahlquist affirme qu’un schéma implicite à \(q=2\) pas consistante et zéro-stable peut être au mieux d’ordre \(\omega=q+2=4\).
Pour que la méthode soit
- au moins d’ordre 2 il faut qu’elle soit consistante et que \(\xi(2)=1\),
- au moins d’ordre 3 il faut qu’elle soit au moins d’ordre 2 et que \(\xi(3)=1\),
- au moins d’ordre 4 il faut qu’elle soit au moins d’ordre 2 et que \(\xi(4)=1\).
Code
q = 2
omega = 3
def xi(i, q):
sa = sum((-j)**i * aa[j] for j in range(q))
sb = b_m1 + sum((-j)**(i-1) * bb[j] for j in range(1, q))
if i == 1:
sb += bb[0]
return (sa).factor() + (i * sb).factor()
def coeff(cas,q):
if CAS_GENERAL:
aa = sympy.symbols(f'a_0:{</span>q<span class="sc">}')
bb = sympy.symbols(f'b_0:{</span>q<span class="sc">}')
b_m1 = sympy.Symbol('b_{-1}')
else : # cas particulier
α = sympy.Symbol('α')
ϑ = sympy.Symbol('ϑ')
aa = [α, 1-α]
bb = [-3*ϑ/2, ϑ/2]
b_m1 = 2
return aa, bb, b_m1
display(Markdown(f"Les conditions de consistance d'ordre {</span>omega<span class="sc">} sont :"))
CAS_GENERAL = True
aa, bb, b_m1 = coeff(CAS_GENERAL, q)
systeme = [sympy.Eq(xi(i, q),1) for i in range(omega)]
display(Markdown(r"$\begin{cases}"+' '.join([r"\xi("+str(i)+")="+sympy.latex(s)+r"\\" for i,s in enumerate(systeme)]) + r"\end{cases}$"))
display(Markdown(r"Ce qui donne le système suivant :"))
CAS_GENERAL = False
aa, bb, b_m1 = coeff(CAS_GENERAL, q)
systeme = [sympy.Eq(xi(i, q),1) for i in range(omega)]
display(Markdown(r"$\begin{cases}"+' '.join([sympy.latex(s)+r"\\" for s in systeme]) + r"\end{cases}$"))
display(Markdown(r"La solution est :"))
sol = sympy.solve(systeme)
display(sol)Les conditions de consistance d’ordre 3 sont :
\(\begin{cases}\xi(0)=a_{0} + a_{1} = 1\\ \xi(1)=- a_{1} + b_{0} + b_{1} + b_{-1} = 1\\ \xi(2)=a_{1} - 2 \left(b_{1} - b_{-1}\right) = 1\\\end{cases}\)
Ce qui donne le système suivant :
\(\begin{cases}\text{True}\\ α - ϑ + 1 = 1\\ - α - ϑ + 5 = 1\\\end{cases}\)
La solution est :
\(\displaystyle \left\{ α : 2, \ ϑ : 2\right\}\)
Dans notre cas
- la méthode est consistante ssi \(\vartheta=\alpha\) car \(a_0+a_1=\alpha+(1-\alpha)=1\) et \(-a_1+b_0+b_1+b_{-1}=-(1-\alpha)-\frac{3\vartheta}{2}+\frac{\vartheta}{2}+2=\alpha-\vartheta+1\);
- pour que la méthode sois d’ordre au moins 2 il faudrait avoir \(1= a_1-2(b_1-b_{-1})=1-\alpha-2(\frac{\alpha}{2}-2)=5-2\alpha\) ce qui n’est pas compatible avec la condition de zéro-stabilité.
Conclusion: si \(0\le\alpha=\vartheta<1\) le schéma est convergent à l’ordre 1, dans les autres cas il n’est pas convergente.
Q3 [3 points]
Nous allons maintenant fixer \(\alpha\). Pour cela, écrivez votre nom et prénom dans la cellule ci-dessous et vous obtiendrez un choix pour le paramètre \(\alpha\). Pour \(\vartheta\), choisir une valeur qui garantie la convergence.Vérifier empiriquement l’ordre de convergence sur le problème de Cauchy
\( \begin{cases} y'(t) = t^2-y(t), &\forall t \in I=[0,1],\\ y(0) = 2, \end{cases} \)
Code
\(\displaystyle \mathtt{\text{α =}}\frac{5}{8}\)
- Pour estimer les erreurs on définit la solution exacte (calculée en utilisant le module
sympyou à la main).
- On calcule la solution approchée pour différentes valeurs de \(N\). Pour le calcul de l’ordre de convergence on initialise la suite avec la solution exacte.
Code
# variables globales
t0 = 0
tfinal = 1
y0 = 2
phi = lambda t,y: t**2-y
##############################################
# solution exacte
##############################################
t = sympy.Symbol('t')
y = sympy.Function('y')
edo = sympy.Eq( sympy.diff(y(t),t) , phi(t,y(t)) )
solpar = sympy.dsolve(edo, ics={y(t0):y0}).simplify()
display(solpar)
sol_exacte = sympy.lambdify(t,solpar.rhs,'numpy')
##############################################
# schéma (initialisation avec sol exacte pour ordre de convergence)
##############################################
def multipas(phi, tt, sol_exacte):
h = tt[1] - tt[0]
uu = np.zeros_like(tt)
uu[:q] = sol_exacte(tt[:q])
for n in range(q-1,len(tt) - 1):
eq = lambda x : -x+my_alpha*uu[n]+(1-my_alpha)*uu[n-1]+h*(2*phi(tt[n+1],x)-3*my_alpha/2*phi(tt[n],uu[n])+my_alpha/2*phi(tt[n-1],uu[n-1]))
temp = fsolve( eq ,uu[n])
uu[n+1] = temp[0]
return uu
##############################################
# ordre
##############################################
H = []
err = []
N = 50
plt.figure(figsize=(16,5))
ax1 = plt.subplot(1,2,1)
ax2 = plt.subplot(1,2,2)
for k in range(4):
N += 20
tt = np.linspace(t0, tfinal, N + 1)
H.append( tt[1] - tt[0] )
yy = sol_exacte(tt)
uu = multipas(phi, tt, sol_exacte)
err.append( np.linalg.norm(uu-yy,np.inf) )
ax1.plot(tt,uu,label=f'Approchée avec N={</span>N<span class="sc">}')
ax1.plot(tt,yy,label='Exacte')
ax1.set_xlabel('$t$')
ax1.set_ylabel('$y$')
ax1.grid(True)
ax1.legend()
ax2.loglog( H, err, 'r-o')
ax2.set_xlabel('$h$')
ax2.set_ylabel('$e$')
ax2.set_title(f'Multipas ordre = {</span>np<span class="sc">.</span>polyfit(np.log(H),np.log(err),<span class="dv">1</span>)[<span class="dv">0</span>]<span class="sc">:1.2f}')
ax2.grid(True)\(\displaystyle y{\left(t \right)} = t^{2} - 2 t + 2\)
2 Exercice 2 : étude d’un système
Soit le problème de Cauchy \(\begin{cases} y'(t)=\eta z(t),\\ z'(t)=y(t)+\eta z(t),\\ y(0)=1,\\ z(0)=1. \end{cases}\)
Pour fixer \(\eta\), écrivez votre nom et prénom dans la cellule ci-dessous et vous obtiendrez un choix pour ce paramètre. Cela fixera aussi le nombre de points \(N\).
Code
%reset -f
%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
from scipy.optimize import fsolve
import sympy
sympy.init_printing()
from IPython.display import display, Math, Markdown
prlat= lambda *args: display(Math(''.join( sympy.latex(arg) for arg in args )))
nom = "Faccanoni"
prenom = "Gloria"
L = list(range(-5,0))
idx = sum([ord(c) for c in nom+prenom])%len(L)
eta = L[idx]
display(Math(r'\eta='+sympy.latex(eta)))
N = -15*eta
print(f'{</span>N <span class="op">=</span> <span class="sc">}')\(\displaystyle \eta=-1\)
N = 15Q1 [1 point]
Calculer la solution exacte.
Calculons la solution exacte avec sympy par exemple:
Code
t = sympy.Symbol('t')
y = sympy.Function('y')
z = sympy.Function('z')
phi1 = lambda t,y,z : eta*z
phi2 = lambda t,y,z : y+eta*z
edo1 = sympy.Eq( sympy.diff(y(t),t) , phi1(t,y(t),z(t)) )
edo2 = sympy.Eq( sympy.diff(z(t),t) , phi2(t,y(t),z(t)) )
# display(edo1)
# display(edo2)
solpar_1, solpar_2 = sympy.dsolve([edo1,edo2],[y(t),z(t)], ics={y(t0):y0, z(t0):z0})
display(solpar_1,solpar_2)\(\displaystyle y{\left(t \right)} = - \frac{\sqrt{3} e^{- \frac{t}{2}} \sin{\left(\frac{\sqrt{3} t}{2} \right)}}{3} + e^{- \frac{t}{2}} \cos{\left(\frac{\sqrt{3} t}{2} \right)}\)
\(\displaystyle z{\left(t \right)} = \frac{\sqrt{3} e^{- \frac{t}{2}} \sin{\left(\frac{\sqrt{3} t}{2} \right)}}{3} + e^{- \frac{t}{2}} \cos{\left(\frac{\sqrt{3} t}{2} \right)}\)
On remarque que \(y(t)\xrightarrow[t\to+\infty]{}0\) et \(z(t)\xrightarrow[t\to+\infty]{}0\)
Code
func_1 = sympy.lambdify(t,solpar_1.rhs,'numpy')
func_2 = sympy.lambdify(t,solpar_2.rhs,'numpy')
tt = np.linspace(t0,tfinal,N+1)
h = tt[1]-tt[0]
plt.figure(figsize=(12,5))
yy = func_1(tt)
zz = func_2(tt)
plt.subplot(1,2,1)
plt.plot(tt,yy,'-*',tt,zz,'-*')
plt.legend([r'$t\mapsto y(t)$',r'$t\mapsto z(t)$'])
plt.subplot(1,2,2)
plt.plot(yy,zz,'-*')
plt.xlabel(r'$y$')
plt.ylabel(r'$z$')
plt.axis('equal');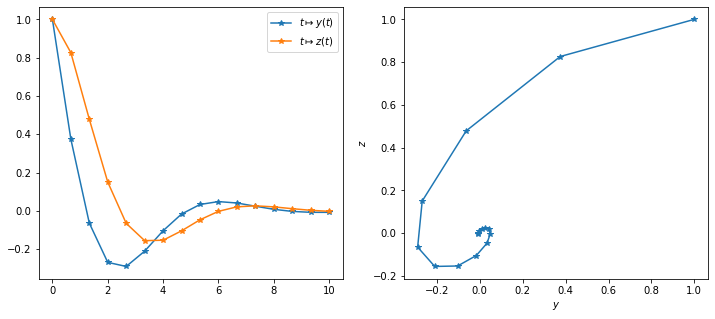
Dans la suite on notera \(u_n\approx y(t_n)\) et \(w_n\approx z(t_n)\).
Pour l’affichage des solutions exactes VS approchées, on peut écrire une fonction qui prend en paramètres la discrétisation tt, les deux listes solution exacte yy et zz, les deux listes solution approchée uu et ww et pour finir une chaîne de caractères s qui contient le nom du schéma.
NOTA BENE : on a juste fixé le nombre de points mais nous n’avons pas fixé la taille du domaine. On regardera la solution exacte pour choisir un \(T\) final significatif.
Code
def affichage(tt,yy,zz,uu,ww,s):
plt.figure(figsize=(12,5))
plt.subplot(1,2,1)
plt.plot(tt,uu,'o--',tt,ww,'d--')
plt.plot(tt,yy,tt,zz)
plt.xlabel('t')
plt.legend([r'$u(t)$ approchée',r'$w(t)$ approchée','$y(t)$ exacte','$z(t)$ exacte'])
plt.title(f'{</span>s<span class="sc">} - y(t) et z(t)')
plt.grid()
plt.subplot(1,2,2)
plt.plot(uu,ww,'o--')
plt.plot(yy,zz)
plt.xlabel('y')
plt.ylabel('z')
plt.legend(['Approchée','Exacte'])
plt.title(f'{</span>s<span class="sc">} - z(y)')
plt.grid()
plt.axis('equal');Q2 [3 points]
Calculer la solution approchée obtenue par la méthode d’Euler modifié.
Afficher \(t\mapsto y(t)\), \(t\mapsto z(t)\) et \(y\mapsto z(y)\) en comparant solution exacte et solution approchée.
\( \text{(EM) } \begin{cases} u_0=1,\\ w_0=0,\\ \tilde u=u_n+\frac{h}{2}\varphi_1(t_n,u_n,w_n),\\ \tilde w=w_n+\frac{h}{2}\varphi_2(t_n,u_n,w_n),\\ u_{n+1}=u_n+h\varphi_1\left(t_n+\frac{h}{2},\tilde u,\tilde w\right),\\ w_{n+1}=w_n+h\varphi_2\left(t_n+\frac{h}{2},\tilde u,\tilde w\right). \end{cases} \)
Code
# x0, y0, h variables globales
def EM(phi1,phi2,tt):
uu, ww = np.zeros_like(tt), np.zeros_like(tt)
uu[0], ww[0] = y0, z0
for n in range(len(tt)-1):
uu_tmp = uu[n]+h/2*phi1(tt[n],uu[n],ww[n])
ww_tmp = ww[n]+h/2*phi2(tt[n],uu[n],ww[n])
uu[n+1] = uu[n]+h*phi1(tt[n]+h/2,uu_tmp,ww_tmp)
ww[n+1] = ww[n]+h*phi2(tt[n]+h/2,uu_tmp,ww_tmp)
return [uu,ww]
[uu, ww] = EM(phi1,phi2,tt)
affichage(tt,yy,zz,uu,ww,"Euler modifié")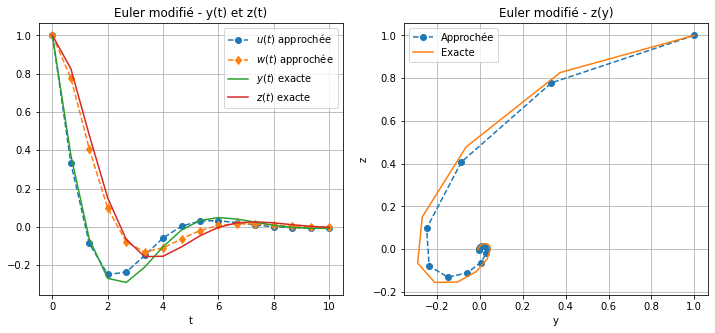
Q3 [3 points]
Calculer la solution approchée obtenue par la méthode de Crank-Nicolson.
Afficher \(t\mapsto y(t)\), \(t\mapsto z(t)\) et \(y\mapsto z(y)\) en comparant solution exacte et solution approchée.
\( \text{(CN) } \begin{cases} u_0=1,\\ w_0=0,\\ u_{n+1}=u_n+\frac{h}{2}\left(\varphi_1(t_{n+1},u_{n+1},w_{n+1})+\varphi_1(t_{n},u_{n},w_{n})\right),\\ w_{n+1}=w_n+\frac{h}{2}\left(\varphi_2(t_{n+1},u_{n+1},w_{n+1})+\varphi_2(t_{n},u_{n},w_{n})\right). \end{cases} \)
Code
from scipy.optimize import fsolve
# x0,y0, h variables globales
def CN(phi1,phi2,tt):
uu, ww = np.zeros_like(tt), np.zeros_like(tt)
uu[0], ww[0] = y0, z0
for n in range(len(tt)-1):
sys = lambda z : [ -z[0]+uu[n]+h/2*phi1(tt[n],uu[n],ww[n])+h/2*phi1(tt[n+1],z[0],z[1]) , -z[1]+ww[n]+h/2*phi2(tt[n],uu[n],ww[n])+h/2*phi2(tt[n+1],z[0],z[1]) ]
uu[n+1], ww[n+1] = fsolve( sys , (uu[n],ww[n]) )
return [uu,ww]
[uu, ww] = CN(phi1,phi2,tt)
affichage(tt,yy,zz,uu,ww,"Crank Nicolson")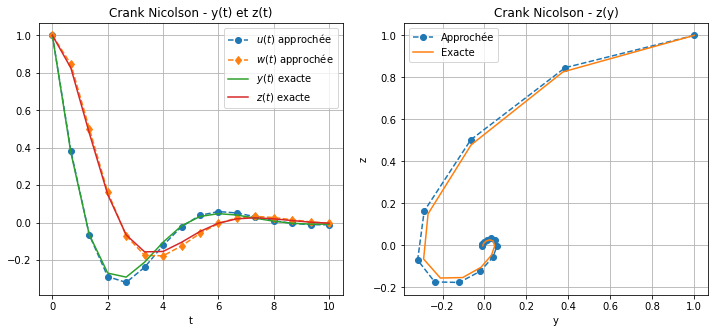
Dans ce cas particulier il est possible d’expliciter cette récurrence en exploitant la linéarité des \(\varphi_1\) et \(\varphi_2\): \( \text{(CN) } \begin{cases} u_0=1,\\ w_0=0,\\ u_{n+1}=u_n+\frac{h}{2}\eta \left(w_{n+1}+w_{n}\right),\\ w_{n+1}=w_n+\frac{h}{2}\left(u_{n+1}+ u_{n}\right)+\frac{h}{2}\eta\left(w_{n+1}+\eta w_{n}\right) \end{cases} \) ce qui donne le schéma explicite calculé ci-dessous par sympy:
Code
t_n = sympy.Symbol('t_n')
dt = sympy.Symbol('h')
t_np1 = t_n+dt
u_n = sympy.Symbol(r'u_{n}')
u_np1 = sympy.Symbol(r'u_{n+1}')
w_n = sympy.Symbol(r'w_{n}')
w_np1 = sympy.Symbol(r'w_{n+1}')
Eq1 = sympy.Eq (u_np1, u_n+dt/2*(phi1(t_n,u_n,w_n)+phi1(t_np1,u_np1,w_np1)) )
Eq2 = sympy.Eq (w_np1, w_n+dt/2*(phi2(t_n,u_n,w_n)+phi2(t_np1,u_np1,w_np1)) )
# prlat(Eq1)
# prlat(Eq2)
sol = sympy.solve([Eq1,Eq2],(u_np1,w_np1))
prlat(u_np1,"=",sol[u_np1].factor(u_n))
prlat(w_np1,"=",sol[w_np1].factor(w_n))\(\displaystyle u_{n+1}\mathtt{\text{=}}- \frac{4 h w_{n} + u_{n} \left(h^{2} - 2 h - 4\right)}{h^{2} + 2 h + 4}\)
\(\displaystyle w_{n+1}\mathtt{\text{=}}- \frac{- 4 h u_{n} + w_{n} \left(h^{2} + 2 h - 4\right)}{h^{2} + 2 h + 4}\)
Code
# x0,y0, h variables globales
def CN(tt):
uu, ww = np.zeros_like(tt), np.zeros_like(tt)
uu[0], ww[0] = y0, z0
for n in range(len(tt)-1):
uu[n+1] = -((h**2-2*h-4)*uu[n]+4*h*ww[n])/(h**2+2*h+4)
ww[n+1] = -((h**2+2*h-4)*ww[n]-4*h*uu[n])/(h**2+2*h+4)
return [uu,ww]
[uu, ww] = CN(tt)
affichage(tt,yy,zz,uu,ww,"Crank Nicolson")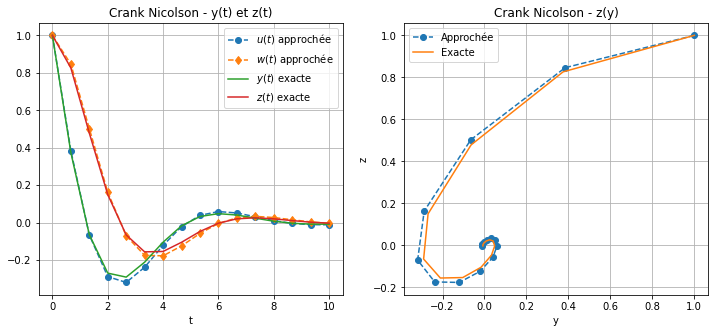
Q5 [1 point]
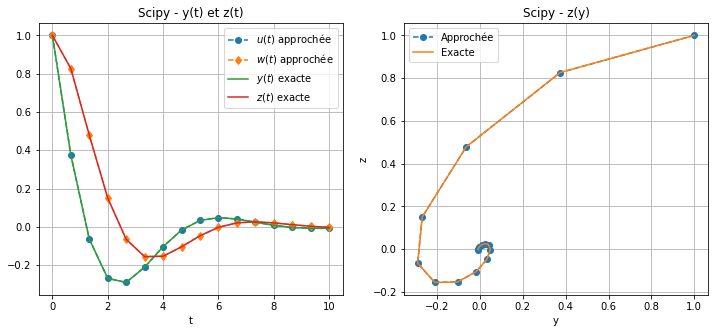
Calculer la solution approchée obtenue par la fonctionodeintdu modulescipy.
Afficher \(t\mapsto y(t)\), \(t\mapsto z(t)\) et \(y\mapsto z(y)\) en comparant solution exacte et solution approchée.
3 Exercice 3 : étude de la A-stabilité d’un schéma
Soit le schéma
\(\begin{cases} u_0=y(t_0)=y_0,\\ \tilde u_{n+1/2}=u_n+\frac{h}{4}\left(\varphi(t_{n},u_{n})+\varphi(t_{n}+\frac{h}{2},\tilde u_{n+1/2})\right),\\ u_{n+1}=u_n+h \varphi\left(t_n+\frac{h}{2},\tilde u_{n+1/2}\right)& n=0,1,2,\dots N-1 \end{cases}\)
- Étudier théoriquement la A-stabilité du schéma.
- Approcher la solution du problème de Cauchy suivant avec le schéma donné d’abord avec 120 points puis avec 130 points. Commenter le résultat.
\(\begin{cases} y'(t)=-50y(t), &t\in[0;10]\\ y(0)=1 \end{cases}\)
Q1 [3 points] Étudier théoriquement la A-stabilité du schéma.
Soit \(\beta>0\) un nombre réel positif et considérons le problème de Cauchy \(y'(t)=-\beta y(t)\) pour \(t>0\) avec \(y(0)=1\). Sa solution est \(y(t)=e^{-\beta t}\) donc \(\lim\limits_{t\to+\infty}|y(t)|=0\).
Le schéma appliqué à ce problème de Cauchy s’écrit
\( \begin{cases} u_0=y(t_0)=y_0,\\ \tilde u_{n+1/2}=u_n-\frac{\beta h}{4}u_{n}-\frac{\beta h}{4}\tilde u_{n+1/2},\\ u_{n+1}=u_n-\beta h \tilde u_{n+1/2}& n=0,1,2,\dots N-1 \end{cases} \)
d’où
\( u_{n+1} = \left( 1-\beta h\frac{4-\beta h}{4+\beta h} \right)u_n \)
Vérifions ces calculs:
Code
# pour ne pas effacer l'affectation de "h", ici je vais l'appeler "dt" mais afficher "h"
dt = sym.Symbol('h')
beta = sym.Symbol(r'\beta')
u_np1 = sym.Symbol(r'u_{n+1}')
sym.var('u_n,x')
u_tilde = sym.solve (-x + u_n - beta*dt/4*u_n-beta*dt/4*x, x)[0]
display(Math(r'\tilde u='+sym.latex(u_tilde)))
u_np1 = (u_n-beta*dt*u_tilde).factor()
display(Math('u_{n+1}='+sym.latex(u_np1)))\(\displaystyle \tilde u=\frac{u_{n} \left(- \beta h + 4\right)}{\beta h + 4}\)
\(\displaystyle u_{n+1}=\frac{u_{n} \left(\beta^{2} h^{2} - 3 \beta h + 4\right)}{\beta h + 4}\)
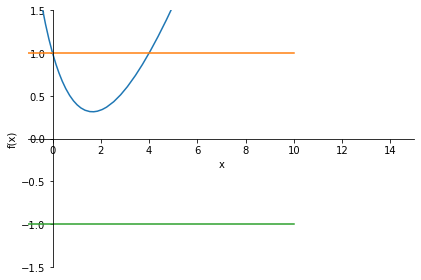
On note \(x=\beta h\). Le schéma est A-stable ssi \(|q(x)|<1\). On étudie alors la fonction \(q\colon \mathbb{R}^+\to\mathbb{R}\) définie par \(q(x)=\dfrac{x^2-3x+4}{4+x}\).
Code
sym.var('x',nonnegative=True)
display(Markdown(r'Dans $\mathbb{R}^+$ on étudie la fonction'))
q = (x**2-3*x+4)/(x+4)
display(Math('q(x)='+sym.latex(q)))
display(Markdown('Limites aux bornes du domaine de definition:'))
display(Math('q(0)='+sym.latex(q.subs(x,0))))
lim=sym.Limit(q,x,sym.oo)
display(Math(sym.latex(lim)+'='+sym.latex(lim.doit())))
display(Markdown(r'On cherche les points stationnaires dans $\mathbb{R}^+$ :'))
dq=(q.diff(x)).factor()
display(Math("q'(x)="+sym.latex(dq)))
display(Markdown("On remarque que le numerateur de q' est une parabole et on a"))
sol=sym.solve(dq)
display(Math("q'(x)=0 \iff x\in"+sym.latex(sol)))
display(Markdown("De plus $q'(x)>0$ ssi $x$ est supérieur à cette valeur, donc"))
minimum=sol[0]
display(Math("x="+sym.latex(minimum)+"\\text{ est un minimum et}"))
qmin=q.subs(x,sol[0])
display(Math("q("+sym.latex(minimum)+")="+sym.latex(qmin)+"="+str(float(qmin))+">0"))
display(Markdown("Donc $q(x)>0$ pour tout $x$."))
display(Markdown("De plus, on a $q(x)<1$ ssi"))
display(sym.solve(q<1))
display(Markdown("Conclusion: $-1<q(x)<1$ pour tout $x<4$."))
sym.plot(q,1,-1,xlim=[-1,15],ylim=[-1.5,1.5]);Dans \(\mathbb{R}^+\) on étudie la fonction
\(\displaystyle q(x)=\frac{x^{2} - 3 x + 4}{x + 4}\)
Limites aux bornes du domaine de definition:
\(\displaystyle q(0)=1\)
\(\displaystyle \lim_{x \to \infty}\left(\frac{x^{2} - 3 x + 4}{x + 4}\right)=\infty\)
On cherche les points stationnaires dans \(\mathbb{R}^+\) :
\(\displaystyle q'(x)=\frac{x^{2} + 8 x - 16}{\left(x + 4\right)^{2}}\)
On remarque que le numerateur de q’ est une parabole et on a
\(\displaystyle q'(x)=0 \iff x\in\left[ -4 + 4 \sqrt{2}\right]\)
De plus \(q'(x)>0\) ssi \(x\) est supérieur à cette valeur, donc
\(\displaystyle x=-4 + 4 \sqrt{2}\text{ est un minimum et}\)
\(\displaystyle q(-4 + 4 \sqrt{2})=\frac{\sqrt{2} \left(- 12 \sqrt{2} + \left(-4 + 4 \sqrt{2}\right)^{2} + 16\right)}{8}=0.3137084989847604>0\)
Donc \(q(x)>0\) pour tout \(x\).
De plus, on a \(q(x)<1\) ssi
\(\displaystyle 0 < x \wedge x < 4\)
Conclusion: \(-1<q(x)<1\) pour tout \(x<4\).
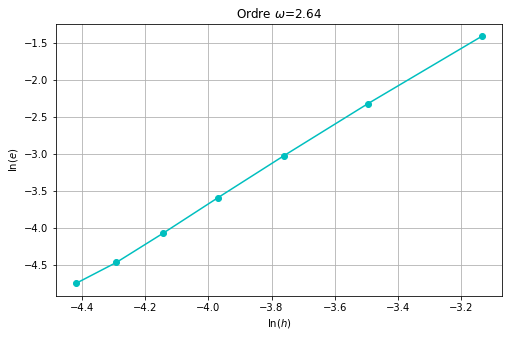
Q2 [2 points] Approcher la solution du problème de Cauchy suivant avec le schéma donné d’abord avec 120 points puis avec 130 points. Commenter le résultat. \(\begin{cases} y'(t)=-50y(t), &t\in[0;10]\\ y(0)=1 \end{cases}\)
Pour la A-stabilité il faut que \(h=\frac{10-0}{N}\) soit \(<\frac{4}{\beta}\) donc \(N>\frac{(10-0)\beta}{4}=\frac{10\times50}{4}=125\). De plus, le problème est stiff.
Code
def schema(tt,phi,y0):
uu = np.zeros_like(tt)
uu[0] = y0
h = tt[1]-tt[0]
for n in range(len(tt)-1):
u_tilde = fsolve ( lambda x : -x+uu[n]+h/4*phi(tt[n],uu[n])+h/4*phi(tt[n+1],x) , uu[n] )[0]
uu[n+1] = uu[n]+h*phi(tt[n]+h/2,u_tilde)
return uu
t0, y0, tfinal = 0, 1, 10
beta = 50
phi = lambda t,y : -beta*y
sol_exacte = lambda t : np.exp(-beta*t)
fig, ax = plt.subplots(nrows=1, ncols=2,figsize=(12,5))
for i,N in enumerate([120, 130]) :
tt = np.linspace(t0,tfinal,N+1)
h = tt[1]-tt[0]
yy = sol_exacte(tt)
uu = schema(tt,phi,y0)
ax[i].plot(tt,yy,'b-',label=("Exacte"))
ax[i].plot(tt,uu,'ro',label=("RK"))
ax[i].set_title(rf' $\beta h$={</span>beta<span class="op">*</span>h<span class="sc">:g}')
ax[i].set_xlabel('$t$')
ax[i].set_ylabel('$u$')
ax[i].legend()
ax[i].grid(True);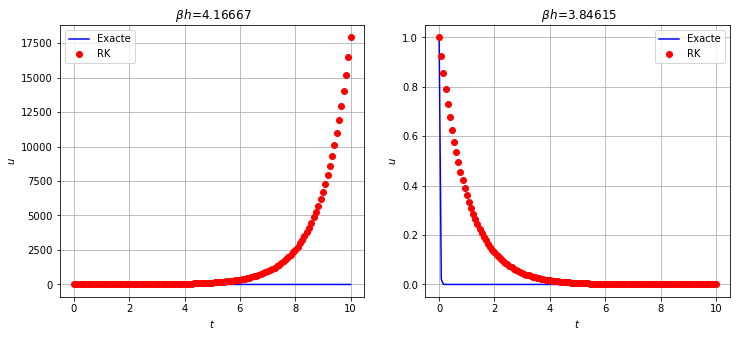
Code
H = []
err = []
N = 130
for k in range(7):
N += 100
tt = np.linspace(t0, tfinal, N + 1)
h = tt[1] - tt[0]
yy = sol_exacte(tt)
uu = schema(tt,phi,y0)
H.append(h)
err.append(np.linalg.norm(uu-yy,np.inf))
omega = np.polyfit(np.log(H),np.log(err), 1)[0]
plt.figure(figsize=(8,5));
plt.plot(np.log(H), np.log(err), 'c-o')
plt.xlabel('$\ln(h)$')
plt.ylabel('$\ln(e)$')
plt.title(rf'Ordre $\omega$={</span>omega<span class="sc">:1.2f}')
plt.grid(True);