2022 Contrôle Terminal session 2

Auteur·rice

Gloria FACCANONI

Date de publication

24 mars 2024

⏱ 2H30
✍ Deposer votre notebook .ipynb sur Moodle (dépôt de devoir)

1 Exercice 1 : Méthode d’Euler exponentielle et problèmes raides

Soient $b,g>0$ deux constantes et considérons le problème de Cauchy

$\begin{cases} y'(t)=-by(t)+g,& t\in[0;1]\\ y(0)=1+10^{-8}. \end{cases}$

Calculer et tracer le graphe de la solution exacte $t\mapsto y(t)$ d’abord pour $b=g=10$ puis pour $b=g=100$.
Méthode d’Euler exponentielle La méthode d’Euler exponentielle appliquée à ce problème de Cauchy s’écrit comme suit:

$ \text{(EEx) }\begin{cases}u_0=y_0,\\u_{n+1}=e^{-bh}u_n+ghf(-bh), & n=0,\dots, N-1\end{cases} $

où $f(z)=\frac{e^z-1}{z}$.
- Vérifier que cette méthode génère une suite arithmético-géométrique et montrer analytiquement qu’elle calcule la solution exacte discrète.
- Soit $b=g=100$. Tracer la solution exacte et les solutions approchées obtenues avec $N=10$, $N=50$, $N=100$.

Q1 [2 points] Solution exacte
Calculer et tracer le graphe de la solution exacte $t\mapsto y(t)$ d’abord pour $b=g=10$ puis pour $b=g=100$.

Il s’agit d’une edo linéaire d’ordre 1 dont la solution est

$ y(t)=\left( y_0-\frac{g}{b} \right)e^{-bt}+\frac{g}{b} \xrightarrow[t\to+\infty]{}y(t)=\frac{g}{b} \text{ pour tout } y(0)=y_0\in\mathbb{R} $

Le problème est numériquement bien posé, c’est-à-dire que l’erreur sur la solution sera au pire de l’ordre de l’erreur sur la condition initiale. Cependant, lorsque $b$ devient de plus en plus grand, la solution devient de plus en plus raide: il s’agit d’un problème stiff.

Code

%reset -f
%matplotlib inline

import numpy as np
import matplotlib.pyplot as plt
from scipy.optimize import fsolve

import sympy 
sympy.init_printing()

from IPython.display import display, Math, Markdown
prlat= lambda *args: display(Math(''.join( sympy.latex(arg) for arg in args )))

Code

# ======================================================
# solution exacte
# ======================================================

exacte = lambda t,b,g,y0 : (y0-g/b)*np.exp(-b*t)+g/b 

# ======================================================
# variables globales
# ======================================================
t0 = 0
tfinal = 1
y0 = 1+1.e-8

# ======================================================
# affichage
# ======================================================
tt = np.linspace(t0,tfinal,101)
plt.figure(figsize=(10,7))
for b in [10,100] :
    plt.plot( tt , exacte(tt,b,b,y0), label=rf'$b=g={</span>b<span class="sc">}$');
plt.legend()
plt.grid()
plt.title('Solution exacte');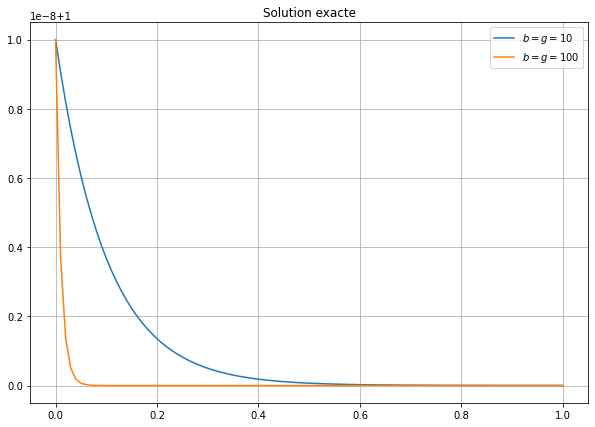

Q2 [4 points] Méthode d’Euler exponentielle La méthode d’Euler exponentielle appliquée à ce problème de Cauchy s’écrit comme suit: $\text{(EEx) }\begin{cases}u_0=y_0,\\u_{n+1}=e^{-bh}u_n+ghf(-bh), & n=0,\dots, N-1\end{cases}$ où $f(z)=\frac{e^z-1}{z}$.
1. Vérifier que cette méthode génère une suite arithmético-géométrique et montrer analytiquement qu’elle calcule la solution exacte discrète. 1. Soit $b=g=100$. Tracer la solution exacte et les solutions approchées obtenues avec $N=10$, $N=50$, $N=100$.

La méthode d’Euler exponentielle donne la suite définie par récurrence

$ \begin{cases} u_0=y_0,\\ u_{n+1}=Au_n+B \end{cases} \qquad\text{avec } A=\exp(-bh), \ B=(\exp(-bh)-1)\frac{g}{b}=(A-1)\frac{g}{b} $

Donc

$ u_{n+1}=Au_n+(A-1)\frac{g}{b}=A\left(u_n+\frac{g}{b}\right)-\frac{g}{b} $

soit encore

$ u_{n+1}+\frac{g}{b} = A\left(u_n+\frac{g}{b}\right). $

Si on note $w_n=u_n+\frac{g}{b}$, on a $ w_{n+1}=Aw_n=A^{n+1}w_0 $

ainsi $ u_n-\frac{g}{b}=(\exp(-hb))^n\left( y_0 -\frac{g}{b}\right). $

Comparons la solution exacte et la solution approchée:

$ \begin{align*} y_n&=\frac{g}{b}+\left( y_0 -\frac{g}{b}\right)e^{-bt_n}\\ u_n&=\frac{g}{b}+\left( y_0 -\frac{g}{b}\right)e^{-bhn} \end{align*} $

Comme $t_n=t_0+nh=nh$, la solution approchée est exacte.

Code

b = 100
g = b

# ======================================================
# SCHÉMA
# ======================================================

def EEx(tt,y0):
    uu = np.zeros_like(tt)
    uu[0] = y0
    h = tt[1]-tt[0]
    for n in range(len(tt)-1):
        K1 = (np.exp(-b*h)-1)/(-b*h)
        uu[n+1] = np.exp(-b*h)*uu[n]+g*h*K1 
    return uu


# ======================================================
# CALCUL SOLUTION APPROCHEE
# ======================================================
plt. figure(1,figsize=(20,7))
for N in [10,50,100]:
    tt = np.linspace(t0,tfinal,N+1)
    uu = EEx(tt,y0)
    plt.plot(tt,uu,'-D',label=f'{</span>N<span class="op">=</span><span class="sc">}')    

yy = exacte(tt,b,b,1+1.e-8)
plt.plot(tt,yy,'-',label='Exacte')
plt.legend()
plt.grid()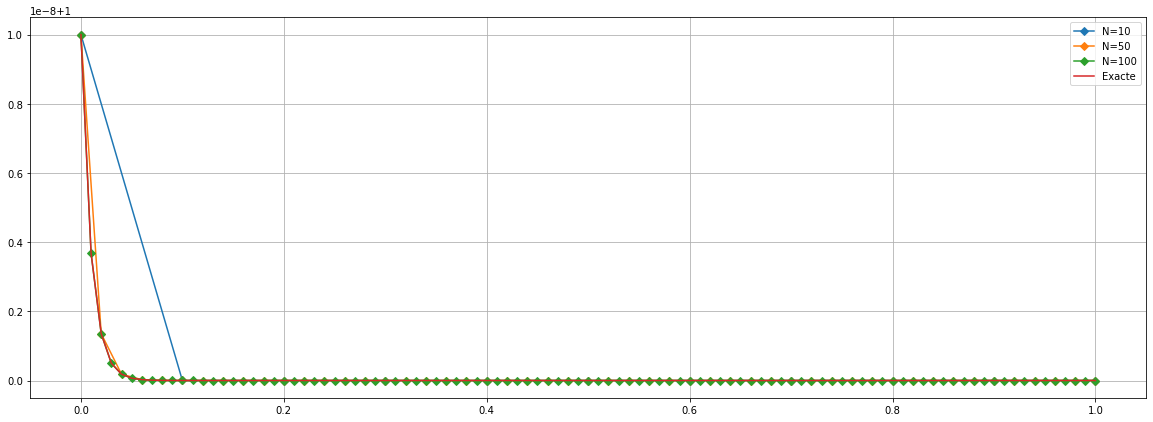

2 Exercice 2 : étude d’un schéma Runge-Kutta

Considérons le schéma dont la matrice de Butcher est donnée ci-dessous:

$ \begin{array}{c|cccc} \frac{1}{2} & \frac{1}{2} & 0 & 0 & 0\\ \frac{2}{3} & \frac{1}{6} & \frac{1}{2}& 0 & 0\\ \frac{1}{2} & -\frac{1}{2} & \frac{1}{2}& \color{red}\vartheta & 0\\ 1 & \frac{3}{2} & -\frac{3}{2}& \frac{1}{2} & \frac{1}{2}\\ \hline & \frac{3}{2} & \color{red}\gamma & \frac{1}{2} & \frac{1}{2} \end{array} $

Calculer $\gamma$ et $\vartheta$ pour que le schéma soit consistant. Dans la suite on posera $\gamma$ et $\vartheta$ égales à ces valeurs.
Étudier empiriquement l’ordre de convergence sur le problème de Cauchy
$ \begin{cases} y'(t) = -\dfrac{y(t)}{2}\left(1-\dfrac{y(t)}{3}\right), &\forall t \in I=[0,10],\\ y(0) = 1, \end{cases} $
Étudier théoriquement l’ordre de convergence du schéma.

Code

%reset -f
%matplotlib inline

import numpy as np
import matplotlib.pyplot as plt
from scipy.optimize import fsolve

import sympy 
sympy.init_printing()

from IPython.display import display, Math, Markdown
prlat= lambda *args: display(Math(''.join( sympy.latex(arg) for arg in args )))

Q1 [1 points] Calculer $\gamma$ et $\vartheta$ pour que le schéma soit consistant. Dans la suite on posera $\gamma$ et $\vartheta$ égales à ces valeurs.

C’est un schéma semi-implicite à $4$ étages ($s=4$).

Pour qu’il soit consistant il faut que $\begin{cases} \displaystyle\sum_{j=1}^s b_{i}=1& \\ \displaystyle c_i=\sum_{j=1}^s a_{ij}&i=1,\dots,s \end{cases}$

Comme $\displaystyle\sum_{j=1}^s b_{i}=\dfrac{3}{2} + \gamma + \dfrac{1}{2} + \dfrac{1}{2}=\dfrac{5}{2} + \gamma$, il faut poser $\color{red}\gamma=-\dfrac{3}{2}$.
La deuxième condition est satisfaite ssi $ = - ++ $, il faut donc poser $= $.

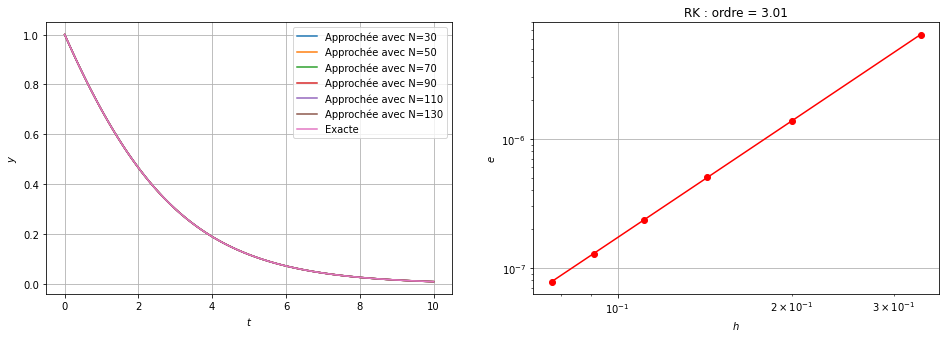
Q2 [5 points] Étudier empiriquement l’ordre de convergence sur le problème de Cauchy $\begin{cases} y'(t) = -\dfrac{y(t)}{2}\left(1-\dfrac{y(t)}{3}\right), &\forall t \in I=[0,10],\\ y(0) = 1, \end{cases} $

Code

# variables globales
t0     = 0
tfinal = 10
y0     = 1

phi = lambda t,y: -y/2*(1-y/3) 

##############################################
# solution exacte
##############################################
t   = sympy.Symbol('t')
y   = sympy.Function('y')
edo = sympy.Eq( sympy.diff(y(t),t) , phi(t,y(t)) )
solpar = sympy.dsolve(edo, y(t), ics={y(t0):y0}).simplify()
display(solpar)

sol_exacte = sympy.lambdify(t,solpar.rhs,'numpy')

##############################################
# solution approchée
##############################################
def RK(tt,phi,y0):
    h = tt[1]-tt[0]
    uu =np.zeros_like(tt)
    uu[0] = y0
    for n in range(len(tt)-1):
        sys = lambda X : [ -X[0]+phi( tt[n]+h/2   ,uu[n]+h/2*X[0]                      ) , 
                           -X[1]+phi( tt[n]+h*2/3 ,uu[n]+h/6*(X[0]+3*X[1])             ), 
                           -X[2]+phi( tt[n]+h/2   ,uu[n]+h/2*(-X[0]+X[1]+X[2])         ), 
                           -X[3]+phi( tt[n+1]     ,uu[n]+h/2*(3*X[0]-3*X[1]+X[2]+X[3]) )
                           ]
        K_start = phi(tt[n],uu[n])
        K1, K2, K3, K4 = fsolve( sys , [K_start,K_start,K_start,K_start] )
        uu[n+1] = uu[n]+h/2*(3*K1-3*K2+K3+K4)
    return uu


##############################################
# ordre
##############################################
H = []
err = []
N = 10

_, (ax1,ax2) = plt.subplots(nrows=1,ncols=2,figsize=(16,5))

for k in range(6):
    N += 20
    tt = np.linspace(t0, tfinal, N + 1)
    H.append( tt[1] - tt[0] )
    yy = sol_exacte(tt)
    uu = RK(tt,phi,y0)
    err.append( np.linalg.norm(uu-yy,np.inf) )
    ax1.plot(tt,uu,label=f'Approchée avec N={</span>N<span class="sc">}')

ax1.plot(tt,yy,label='Exacte')
ax1.set_xlabel('$t$')
ax1.set_ylabel('$y$')
ax1.grid(True)
ax1.legend()

ax2.loglog( H, err, 'r-o')
ax2.set_xlabel('$h$')
ax2.set_ylabel('$e$')
ax2.set_title(f'RK : ordre = {</span>np<span class="sc">.</span>polyfit(np.log(H),np.log(err),<span class="dv">1</span>)[<span class="dv">0</span>]<span class="sc">:1.2f}')
ax2.grid(True)

$\displaystyle y{\left(t \right)} = \frac{3 \left(2 \sqrt{e^{t}} - 1\right)}{4 e^{t} - 1}$

Q3 [3 points] Étudier théoriquement l’ordre de convergence du schéma.

Soit $\omega$ l’ordre de la méthode.

C’est un schéma semi-implicite à $s=4$ étages donc $\omega\le2s=8$
Pour $\vartheta=\frac{1}{2}$ et $\gamma=\frac{3}{2}$, $\omega\ge1$.
Si, de plus, $\displaystyle\sum_{j=1}^s b_j c_j=\frac{1}{2}$ alors $\omega\ge2$
Si, de plus,
$\begin{cases} \displaystyle\sum_{j=1}^s b_j c_j^2=\frac{1}{3}\\ \displaystyle\sum_{i=1}^s\sum_{j=1}^s b_i a_{ij} c_j=\frac{1}{6} \end{cases}$ alors $\omega\ge3$
Si, de plus, $\begin{cases} \displaystyle\sum_{j=1}^s b_j c_j^3=\frac{1}{4}& \\ \displaystyle\sum_{i=1}^s\sum_{j=1}^s b_i c_i a_{ij} c_j=\frac{1}{8} \\ \displaystyle\sum_{i=1}^s\sum_{j=1}^s b_i a_{ij} c_j^2=\frac{1}{12} \\ \displaystyle\sum_{i=1}^s\sum_{j=1}^s\sum_{k=1}^s b_i a_{ij}a_{jk} c_k=\frac{1}{24} \end{cases}$ alors $\omega\ge4$

Calculons donc toutes ces sommes:

Code

def ordre_RK(s, A=None, b=None, c=None):

    j = sympy.symbols('j')
    
    if A is None:
        A = sympy.MatrixSymbol('a', s, s)
    else:
        A = sympy.Matrix(A)
    if c is None:
        c = sympy.symbols(f'c_0:{</span>s<span class="sc">}')    
    if b is None:
        b = sympy.symbols(f'b_0:{</span>s<span class="sc">}')
    
    
    display(Markdown("**Matrice de Butcher**"))
    But = matrice_Butcher(s, A, b, c)
    
    Eqs = []

    # display(Markdown(f"**On a {s+1} conditions pour avoir consistance = pour être d'ordre 1**"))
    # ordre_1(s, A, b, c, j)
    
    display(Markdown("**On doit ajouter 1 condition pour être d'ordre 2**"))
    Eq_2 = ordre_2(s, A, b, c, j)
    Eqs.append(Eq_2)

    display(Markdown("**On doit ajouter 2 conditions pour être d'ordre 3**"))
    Eq_3 = ordre_3(s, A, b, c, j)  
    Eqs.extend(Eq_3)  
    
    display(Markdown("**On doit ajouter 4 conditions pour être d'ordre 4**"))
    Eq_4 = ordre_4(s, A, b, c, j)
    Eqs.extend(Eq_4)

    return Eqs


def matrice_Butcher(s, A, b, c):
    But = sympy.Matrix(A)
    But = But.col_insert(0, sympy.Matrix(c))   
    last = [sympy.Symbol(" ")]
    last.extend(b)
    But = But.row_insert(s,sympy.Matrix(last).T)
    display(Math(sympy.latex(sympy.Matrix(But))))
    return But


def ordre_1(s, A, b, c, j):
    texte = "\sum_{j=1}^s b_j =" + f"{</span><span class="bu">sum</span>(b)<span class="sc">.</span>simplify()<span class="sc">}"
    texte += r"\text{ doit être égale à }1"
    display(Math(texte))
    for i in range(s):
        somma = sympy.summation(A[i,j],(j,0,s-1)).simplify()
        texte = r'\sum_{j=1}^s a_{'</span><span class="op">+</span><span class="bu">str</span>(i)<span class="op">+</span><span class="vs">r'j}=' + sympy.latex( somma )
        texte += r"\text{ doit être égale à }"+sympy.latex(c[i])
        display(Math( texte ))
    return None    


def ordre_2(s, A, b, c, j):
    texte = '\sum_{j=1}^s b_j c_j=' +sympy.latex(sum([b[i]*c[i] for i in range(s)]).simplify())
    texte += r"\text{ doit être égale à }\frac{1}{2}"
    display(Math(texte))
    Eq_2 = sympy.Eq( sum([b[i]*c[i] for i in range(s)]).simplify(), sympy.Rational(1,2) )
    return Eq_2


def ordre_3(s, A, b, c, j):
    texte = '\sum_{j=1}^s b_j c_j^2='
    texte += sympy.latex( sum([b[i]*c[i]**2 for i in range(s)]).simplify() )
    texte += r"\text{ doit être égale à }\frac{1}{3}"
    display(Math(texte))
    Eq_3_1 = sympy.Eq( sum([b[i]*c[i]**2 for i in range(s)]).simplify(), sympy.Rational(1,3) )
    texte = r'\sum_{i,j=1}^s b_i a_{ij} c_j='    
    somma = sum([b[i]*A[i,j]*c[j] for j in range(s) for i in range(s)]).simplify()
    texte = texte + sympy.latex(somma)
    texte += r"\text{ doit être égale à }\frac{1}{6}"
    display(Math(texte))
    Eq_3_2 = sympy.Eq( sum([b[i]*A[i,j]*c[j] for j in range(s) for i in range(s)]).simplify(), sympy.Rational(1,6) )
    return [Eq_3_1, Eq_3_2]


def ordre_4(s, A, b, c, j):
    texte = '\sum_{j=1}^s b_j c_j^3='
    texte += sympy.latex( sum([b[i]*c[i]**3 for i in range(s)]).simplify() )
    texte += r"\text{ doit être égale à }\frac{1}{4}"
    display(Math(texte))
    Eq_4_1 = sympy.Eq( sum([b[i]*c[i]**3 for i in range(s)]).simplify(), sympy.Rational(1,4) )
    texte = r'\sum_{i,j=1}^s b_i c_i a_{ij} c_j='
    somma = sum([b[i]*c[i]*A[i,j]*c[j] for j in range(s) for i in range(s)]).simplify()
    texte = texte + sympy.latex(somma)
    texte += r"\text{ doit être égale à }\frac{1}{8}"
    display(Math(texte))
    Eq_4_2 = sympy.Eq( sum([b[i]*c[i]*A[i,j]*c[j] for j in range(s) for i in range(s)]).simplify(), sympy.Rational(1,8) )
    texte = r'\sum_{i,j=1}^s b_i a_{ij} c_j^2='
    somma = sum([b[i]*A[i,j]*c[j]**2 for j in range(s) for i in range(s)]).simplify()
    texte = texte + sympy.latex(somma)
    texte += r"\text{ doit être égale à }\frac{1}{12}"
    display(Math(texte))
    Eq_4_3 = sympy.Eq( sum([b[i]*A[i,j]*c[j]**2 for j in range(s) for i in range(s)]).simplify(), sympy.Rational(1,12) )
    texte = r'\sum_{i,j,k=1}^s b_i a_{ij} a_{jk} c_k='
    somma = sum([b[i]*A[i,j]*A[j,k]*c[k] for k in range(s) for j in range(s) for i in range(s)]).simplify()
    texte = texte + sympy.latex(somma)
    texte += r"\text{ doit être égale à }\frac{1}{24}"
    display(Math(texte))
    Eq_4_4 = sympy.Eq( sum([b[i]*A[i,j]*A[j,k]*c[k] for k in range(s) for j in range(s) for i in range(s)]).simplify(), sympy.Rational(1,24) )
    return [Eq_4_1, Eq_4_2, Eq_4_3, Eq_4_4]



##################################################
# Conditions avec s étages
##################################################

c = [sympy.Rational(1,2), sympy.Rational(2,3), sympy.Rational(1,2), 1]
b = [ sympy.Rational(3,2), -sympy.Rational(3,2), sympy.Rational(1,2), sympy.Rational(1,2)]
A = [ [sympy.Rational(1,2), 0, 0, 0], 
      [sympy.Rational(1,6), sympy.Rational(1,2), 0, 0],
      [-sympy.Rational(1,2), sympy.Rational(1,2), sympy.Rational(1,2), 0],
      [sympy.Rational(3,2), -sympy.Rational(3,2), sympy.Rational(1,2), sympy.Rational(1,2)]]
s = len(c)


Eqs = ordre_RK(s, A, b, c)

# for eq in Eqs:
#     display(eq)

Matrice de Butcher

$\displaystyle \left[\begin{matrix}\frac{1}{2} & \frac{1}{2} & 0 & 0 & 0\\\frac{2}{3} & \frac{1}{6} & \frac{1}{2} & 0 & 0\\\frac{1}{2} & - \frac{1}{2} & \frac{1}{2} & \frac{1}{2} & 0\\1 & \frac{3}{2} & - \frac{3}{2} & \frac{1}{2} & \frac{1}{2}\\ & \frac{3}{2} & - \frac{3}{2} & \frac{1}{2} & \frac{1}{2}\end{matrix}\right]$

On doit ajouter 1 condition pour être d’ordre 2

$\displaystyle \sum_{j=1}^s b_j c_j=\frac{1}{2}\text{ doit être égale à }\frac{1}{2}$

On doit ajouter 2 conditions pour être d’ordre 3

$\displaystyle \sum_{j=1}^s b_j c_j^2=\frac{1}{3}\text{ doit être égale à }\frac{1}{3}$

$\displaystyle \sum_{i,j=1}^s b_i a_{ij} c_j=\frac{1}{6}\text{ doit être égale à }\frac{1}{6}$

On doit ajouter 4 conditions pour être d’ordre 4

$\displaystyle \sum_{j=1}^s b_j c_j^3=\frac{11}{36}\text{ doit être égale à }\frac{1}{4}$

$\displaystyle \sum_{i,j=1}^s b_i c_i a_{ij} c_j=\frac{5}{48}\text{ doit être égale à }\frac{1}{8}$

$\displaystyle \sum_{i,j=1}^s b_i a_{ij} c_j^2=\frac{5}{72}\text{ doit être égale à }\frac{1}{12}$

$\displaystyle \sum_{i,j,k=1}^s b_i a_{ij} a_{jk} c_k=\frac{1}{48}\text{ doit être égale à }\frac{1}{24}$

D’après ces résultats, le schéma est d’ordre $3$.

3 Exercice 3 : étude d’un schéma multipas

On notera $\varphi_k\stackrel{\text{déf}}{=}\varphi(t_k,u_k)$.

Considérons les deux méthodes multipas

$ u_{n+1}=\frac{18}{11}u_n-\frac{9}{11}u_{n-1}+\frac{2}{11}u_{n-2}+h\frac{6}{11}\varphi_{n+1} $

$ u_{n+1}=\frac{18}{11}u_n-\frac{9}{11}u_{n-1}+\frac{3}{11}u_{n-2}+h\frac{6}{11}\varphi_{n+1} $

Parmi ces deux méthode, indiquer laquelle est consistente (justifier la réponse). Dans la suite on n’étudiera que cette méthode.
Étudier la zéro-stabilité de la méthode.
Étudier théoriquement l’ordre de la méthode.
Vérifier empiriquement l’ordre de convergence sur le problème de Cauchy
$ \begin{cases} y'(t) = -\dfrac{y(t)}{2}\left(1-\dfrac{y(t)}{3}\right), &\forall t \in I=[0,10],\\ y(0) = 1, \end{cases} $

Code

%reset -f
%matplotlib inline

import numpy as np
import matplotlib.pyplot as plt
from scipy.optimize import fsolve

import sympy as sp
sp.init_printing()

from IPython.display import display, Math, Markdown
prlat= lambda *args: display(Math(''.join( sp.latex(arg) for arg in args )))

Q1 [1 points] Choisir la méthode consistente (justifier la réponse). Dans la suite on n’étudiera que cette méthode.

On a $p=2$: c’est des méthodes à $q=p+1=3$ pas.
Les méthodes sont implicites car $b_{-1}=\frac{6}{11}\neq0$.

Pour que la méthode soit consistante il faut que

$ \begin{cases} \xi(0)\stackrel{\text{def}}{=}\displaystyle\sum_{j=0}^p a_j=a_0+a_1=1, \\ \xi(1)\stackrel{\text{def}}{=}\displaystyle\sum_{j=0}^p (-j)a_j+\sum_{j=-1}^p b_j=1. \end{cases}$

Seul la première des méthodes est consistante car

$ \frac{18}{11}-\frac{9}{11}+\frac{2}{11}=1 $

tandis que

$ \frac{18}{11}-\frac{9}{11}+\frac{3}{11}=\frac{12}{11}\neq1. $

Q2 [2 points] Étudier la zéro-stabilité.

Le premier polynôme caractéristique est

$ \varrho(r)= r^{p+1}-\sum_{j=0}^p a_jr^{p-j}= r^3-\frac{18}{11}r^2+\frac{9}{11}r-\frac{2}{11}= \frac{1}{11}(r-1)(11r^2-7r+2). $

Calculons ses racines avec sympy.

Code

aa = [sp.Rational(18,11), sp.Rational(-9,11), sp.Rational(2,11)]
q = len(aa)

r = sp.Symbol('r')
rho = sp.Function(r'\varrho')
p = q-1
rho_gen =  sp.poly(r**(p+1) - sum( aa[j] * r**(p-j) for j in range(p+1)), r)
eq = sp.Eq( rho(r), rho_gen.as_expr() )

display(Markdown(f"Le premier polynome caractéristique est :"))
display(Math( sp.latex(eq,order='old') ) )

display(Markdown(f"Ses racines sont :"))
racines = sp.solve(rho_gen,r)
display(racines)
display(Markdown(f"dont les modules valent :"))
display([abs(rac).evalf() for rac in racines])

Le premier polynome caractéristique est :

$\displaystyle \varrho{\left(r \right)} = - \frac{2}{11} + \frac{9 r}{11} - \frac{18 r^{2}}{11} + r^{3}$

Ses racines sont :

$\displaystyle \left[ 1, \ \frac{7}{22} - \frac{\sqrt{39} i}{22}, \ \frac{7}{22} + \frac{\sqrt{39} i}{22}\right]$

dont les modules valent :

$\displaystyle \left[ 1.0, \ 0.426401432711221, \ 0.426401432711221\right]$

Les racines sont $ r_0=1,\quad r_{1,2}=\frac{7\pm\sqrt{-39}}{22}. $ La méthode est donc zéro-stable car $ \begin{cases} |r_j|\le1 \quad\text{pour tout }j=0,1,2 \\ \varrho'(r_j)\neq0 \text{ si } |r_j|=1. \end{cases} $

Q3 [3 points] Étudier théoriquement l’ordre.

La première barrière de Dahlquist affirme qu’un schéma implicite à $q=3$ pas consistante et zéro-stable peut être au mieux d’ordre $\omega=q+1=4$.

Pour que la méthode soit - au moins d’ordre 2 il faut qu’elle soit consistante et que $\displaystyle\sum_{j=0}^p (-j)^{2}a_j+2\sum_{j=-1}^p (-j)^{1}b_j=1$, - au moins d’ordre 3 il faut qu’elle soit au moins d’ordre 2 et que $\displaystyle\sum_{j=0}^p (-j)^{3}a_j+3\sum_{j=-1}^p (-j)^{2}b_j=1$, - au moins d’ordre 4 il faut qu’elle soit au moins d’ordre 2 et que $\displaystyle\sum_{j=0}^p (-j)^{4}a_j+4\sum_{j=-1}^p (-j)^{3}b_j=1$.

Dans notre cas - la méthode est consistante; - pour que la méthode sois d’ordre au moins 2 il faut de plus $1= a_1+4a_2-2(b_1+2b_2-b_{-1})$ ce qui est satisfait; - pour que la méthode sois d’ordre au moins 3 il faut de plus $1= -a_1-8a_2+3(b_1+4b_2+b_{-1})$ ce qui est satisfait; - pour que la méthode sois d’ordre au moins 4 il faut de plus $1= a_1+16a_2-4(b_1+8b_2-b_{-1})$ ce qui n’est pas satisfait.

La méthode est donc d’ordre 3 (cf. validation avec sympy ci-dessous).

Code

# j = 0...p
# q = p+1 # nb de pas
# ω # ordre de la méthode

CAS_GENERAL = True
p = 2

q = p+1 
ordre_max = q+2 if q%2==0 else q+1

print(f"{</span><span class="st">'★'</span><span class="op">*</span><span class="dv">70</span><span class="sc">}\nC'est une méthode à q = {</span>q<span class="sc">} pas d'ordre ω ≤ {</span>ordre_max<span class="sc">}")


if CAS_GENERAL:
    aa = sympy.symbols(f'a_0:{</span>q<span class="sc">}')
    bb = sympy.symbols(f'b_0:{</span>q<span class="sc">}')
    bm1 = sympy.Symbol('b_{-1}')
else : # cas particulier
    aa = [sympy.Rational(18,11), -sympy.Rational(9,11),sympy.Rational(2,11)]
    bb = [0,0,0]
    bm1 = sympy.Rational(6,11)

i=1
sa=sum( [-j*aa[j] for j in range(len(aa))] )
sb=bm1+sum( [bb[j] for j in range(len(bb))] )
print(f"{</span><span class="st">'★'</span><span class="op">*</span><span class="dv">70</span><span class="sc">}\nLa méthode est d'ordre ω ≥ {</span>i<span class="sc">} (= consistante) si ")
prlat(sum(aa).factor(),"=1" )
prlat((sa).factor()+(i*sb).factor(),"=1")

for i in range(2,ordre_max+1):
    sa=sum( [(-j)**i*aa[j] for j in range(len(aa))] )
    sb=bm1+sum( [(-j)**(i-1)*bb[j] for j in range(1,len(bb))] )
    print(f"{</span><span class="st">'★'</span><span class="op">*</span><span class="dv">70</span><span class="sc">}\nLa méthode est d'ordre ω ≥ {</span>i<span class="sc">} si elle est d'ordre {</span>i<span class="op">-</span><span class="dv">1</span><span class="sc">} et, de plus, ")
    prlat((sa).factor()+(i*sb).factor(),"=1" )

★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★
C'est une méthode à q = 3 pas d'ordre ω ≤ 4
★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★
La méthode est d'ordre ω ≥ 1 (= consistante) si 
★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★
La méthode est d'ordre ω ≥ 2 si elle est d'ordre 1 et, de plus, 
★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★
La méthode est d'ordre ω ≥ 3 si elle est d'ordre 2 et, de plus, 
★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★
La méthode est d'ordre ω ≥ 4 si elle est d'ordre 3 et, de plus,

$\displaystyle a_{0} + a_{1} + a_{2}\mathtt{\text{=1}}$

$\displaystyle - a_{1} - 2 a_{2} + b_{0} + b_{1} + b_{2} + b_{-1}\mathtt{\text{=1}}$

$\displaystyle a_{1} + 4 a_{2} - 2 \left(b_{1} + 2 b_{2} - b_{-1}\right)\mathtt{\text{=1}}$

$\displaystyle - a_{1} - 8 a_{2} + 3 \left(b_{1} + 4 b_{2} + b_{-1}\right)\mathtt{\text{=1}}$

$\displaystyle a_{1} + 16 a_{2} - 4 \left(b_{1} + 8 b_{2} - b_{-1}\right)\mathtt{\text{=1}}$

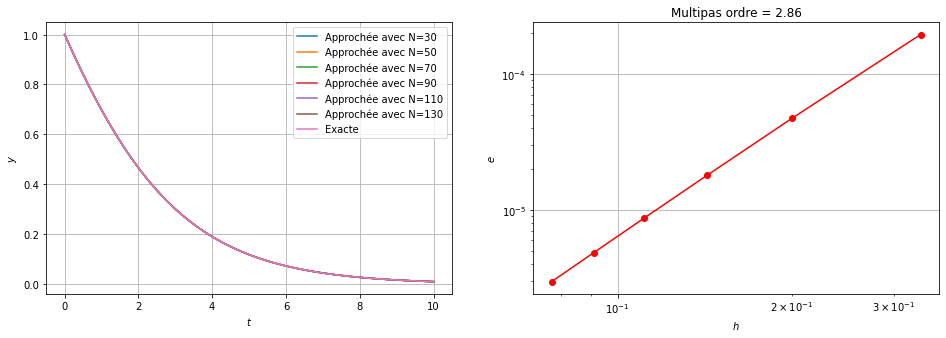
Q4 [3 points] Vérifier empiriquement l’ordre de convergence sur le problème de Cauchy $\begin{cases} y'(t) = -\dfrac{y(t)}{2}\left(1-\dfrac{y(t)}{3}\right), &\forall t \in I=[0,10],\\ y(0) = 1, \end{cases} $

Code

# variables globales
t0     = 0
tfinal = 10
y0     = 1

phi = lambda t,y: -y/2*(1-y/3) #-y-t**2

##############################################
# solution exacte
##############################################
t   = sympy.Symbol('t')
y   = sympy.Function('y')
edo = sympy.Eq( sympy.diff(y(t),t) , phi(t,y(t)) )
solgenLIST = sympy.dsolve(edo)
display(solgenLIST)
solgen=solgenLIST[0]
display(solgen)
consts = sympy.solve( sympy.Eq( y0, solgen.rhs.subs(t,t0)) , dict=True)[0]
display(consts)
solpar = solgen.subs(consts).simplify()
display(solpar)

sol_exacte = sympy.lambdify(t,solpar.rhs,'numpy')

##############################################
# schéma (initialisation avec sol exacte pour ordre de convergence)
##############################################
def multipas(phi, tt, sol_exacte):
    h  = tt[1] - tt[0]
    uu = [sol_exacte(tt[i]) for i in range(3)]
    for i in range(2,len(tt) - 1):
        eq = lambda x : -x+18/11*uu[i]-9/11*uu[i-1]+2/11*uu[i-2]+h*6/11*phi(tt[i+1],x)
        temp = fsolve( eq ,uu[i])
        uu.append( temp[0] )
    return uu

##############################################
# ordre
##############################################
H = []
err = []
N = 10

figure(figsize=(16,5))
ax1 = subplot(1,2,1)

for k in range(6):
    N += 20
    tt = linspace(t0, tfinal, N + 1)
    H.append( tt[1] - tt[0] )
    yy = sol_exacte(tt)
    uu = multipas(phi, tt, sol_exacte)
    err.append( norm(uu-yy,inf) )
    ax1.plot(tt,uu,label=f'Approchée avec N={</span>N<span class="sc">}')

ax1.plot(tt,yy,label='Exacte')
xlabel('$t$')
ylabel('$y$')
ax1.grid(True)
ax1.legend()

ax2 = subplot(1,2,2)
ax2.loglog( H, err, 'r-o')
xlabel('$h$')
ylabel('$e$')
title(f'Multipas ordre = {</span>polyfit(log(H),log(err),<span class="dv">1</span>)[<span class="dv">0</span>]<span class="sc">:1.2f}')
ax2.grid(True)

$\displaystyle \left[ y{\left(t \right)} = \frac{3 \left(e^{C_{1}} - \sqrt{e^{C_{1} + t}}\right)}{e^{C_{1}} - e^{t}}, \ y{\left(t \right)} = \frac{3 \left(e^{C_{1}} + \sqrt{e^{C_{1} + t}}\right)}{e^{C_{1}} - e^{t}}\right]$

$\displaystyle y{\left(t \right)} = \frac{3 \left(e^{C_{1}} - \sqrt{e^{C_{1} + t}}\right)}{e^{C_{1}} - e^{t}}$

$\displaystyle \left\{ C_{1} : - \log{\left(4 \right)}\right\}$

$\displaystyle y{\left(t \right)} = \frac{3 \left(2 \sqrt{e^{t}} - 1\right)}{4 e^{t} - 1}$

Retour au sommet