Les équations différentielles décrivent l’évolution de divers phénomènes dans de nombreux domaines. Elles expriment des relations impliquant une ou plusieurs dérivées d’une fonction inconnue. Lorsque ces dérivées sont toutes prises par rapport à une seule variable, on parle d’équation différentielle ordinaire (EDO), tandis que celles impliquant des dérivées partielles sont qualifiées d’équations aux dérivées partielles (EDP).
1.1 EDO d’ordre \(p\)
Une EDO se présente sous la forme générale:
\( F(y(t),y'(t),y''(t),\dots,y^{(p)}(t))=g(t). \)
Les inconnues sont une fonction\(y\colon I\subset\mathbb{R}\to\mathbb{R}\) et son intervalle de définition\(I\).
Elle combine la fonction inconnue \(y\) et ses dérivées \(y'\), \(y''\), ,\(y^{(p)}\) (où \(p\) est l’ordre de l’équation).
Si la fonction \(g\), appelée “second membre” de l’équation, est nulle, l’équation est dite homogène.
Résoudre une équation différentielle consiste à trouver toutes les fonctions définies sur un intervalle \(I\subset\mathbb{R}\) qui vérifient cette équation (on dit aussi intégrer l’équation différentielle).
Par le terme solution générale d’une EDO on désigne un représentant qui englobe l’ensemble des solutions possibles. L’une des solutions de l’EDO sera appelée solution particulière. On appelle courbes intégrales d’une EDO les courbes représentatives des solutions de l’équation.
Exemple
La résolution de l’équation différentielle \(y'(t)=-y(t)\) consiste à trouver toutes les fonctions \(y(t)\) telles que \(y'(t)=-y(t)\) pour tout \(t\in I\). On peut vérifier que \(y(t)=ce^{-t}\) pour tout \(t\in\mathbb{R}\) (où \(c\) est une constante réelle arbitraire) est une solution de l’EDO. En particulier, pour \(c=0\), on obtient la solution nulle.
1.1.1 Représentations graphiques poir une EDO d’ordre 1 : champ de vecteurs et lignes de courant
Bien qu’il soit très rare que l’on puisse résoudre explicitement une équation différentielle donnée, comprendre l’allure des solutions peut être facilité en examinant le champ de vecteurs correspondant. Les graphes des solutions d’une équation différentielle \(y'(t)=\varphi(t,y(t))\) sont, par définition, tangents à leur vecteur vitesse \((1,y'(t))\), donc au vecteur dérivé \((1, \varphi(t,y(t))\). Même sans connaître explicitement les solutions, connaître la fonction en chaque point permet de représenter ces vecteurs tangents. En traçant un grand nombre de ces vecteurs uniformément répartis dans le plan, on obtient le champ de vecteurs associé à l’équation différentielle. Cette représentation permet souvent de deviner les graphes des solutions, ces courbes étant tangentes en tous leurs points aux vecteurs du champ.
La fonction quiver du module matplt.plotlib permet de tracer un champ de vecteurs: quiver(x_pos, y_pos, x_dir, y_dir, color)
La fonction streamplt.plot permet de tracer des lignes de courant représentant un champ vectoriel.
Utilisons-les pour obtenir les tracés associés à l’équation différentielle de notre exemple.
# On représente en général un champ de vecteurs en des points régulièrement espacés de $ I\times\mathbb{R} $ et en normalisant les vecteurs. # Dessinons alors, en chaque point (t,y) de la grille un vecteur $\mathbf{V}_{t,y}$ de pente $\varphi(t,y)$ : le graphe de $f$ est tangent en chaque point $(t,y)$ au vecteur $\mathbf{V}_{t,y}$. # Remarquer qu'**on n'a pas besoin d'avoir résolu l'équation (analytiquement) pour pouvoir dessiner le champ de tangentes, et ceci permet parfois d'avoir une idée du comportement des solutions.**import numpy as npimport matplotlib.pyplot as pltphi =lambda t,y : -yg1 = np.linspace(0,4,21)g2 = np.linspace(-5,5,21)T,Y = np.meshgrid(g1,g2) # compute direction at each pointDT, DY =1, phi(T,Y) # compute growth rate on the plt.grid# M = np.sqrt(DT**2+DY**2) # norm growth rate M = np.hypot(DT,DY)plt.figure(figsize=(10,3))# Champ des pentesplt.subplot(1,2,1)# plt.quiver(T,Y, DT/M, DY/M, M, pivot='mid')plt.quiver(T,Y, DT/M, DY/M, M, cmap = plt.cm.viridis, scale_units='xy',scale=3.)plt.grid()plt.xlabel('t')plt.ylabel('y')plt.title('Champ des pentes');# Lignes de courantplt.subplot(1,2,2)# plt.streamplot(T,Y, DT/M, DY/M, color=M)plt.streamplot(T,Y, DT/M, DY/M, color=M, linewidth=1, cmap=plt.cm.viridis, density=2, arrowstyle='->', arrowsize=1.5)plt.grid()plt.xlabel('t')plt.ylabel('y')plt.title('Lignes de courant')plt.show();
1.2 EDO d’ordre supérieur à 1 \(\leadsto\) Système d’EDOs d’ordre 1
Une EDO d’ordre \(p\) est dite normalisée lorsqu’elle est exprimée sous la forme:
1.2.1 Représentations graphiques pour un système de 2 EDO d’ordre 1 : portait de phase
TO DO
1.3 Conditions Initiales
Les EDO ont généralement une infinité de solutions. Pour déterminer la solution appropriée qui représente le problème physique, il est nécessaire de prendre en compte des données supplémentaires.
Définition
Soit une EDO d’ordre \(p\). Une condition initiale (CI) est un ensemble de relations du type:
qui imposent en \(t_0\) les valeurs respectives de la fonction inconnue et de ses dérivées.
2 Problème de Cauchy
Le problème associé à une EDO avec une condition initiale est connu sous le nom de problème de Cauchy:
Définition: Problème de Cauchy
Considérons un intervalle \(I\subset\mathbb{R}\), un point \(t_0\) dans \(I\), une fonction \(\varphi \colon I \times \mathbb{R} \to \mathbb{R}\) continue. Le problème de Cauchy est défini comme la recherche d’une fonction réelle \(y\in\mathcal{C}^1(I)\) telle que
Nous concentrerons notre analyse principalement sur le cas où une seule EDO est présente, c’est-à-dire le cas scalaire.
Résoudre un problème de Cauchy, c’est rechercher toutes les fonctions, définies sur un intervalle \(I\subset\mathbb{R}\), qui satisfont l’équation différentielle tout en vérifiant la condition initiale. Cela soulève des questions naturelles telles que :
trouver toutes les fonctions solutions de l’EDO,
parmi ces fonctions, choisir celles qui respectent la CI (existence? unicité?),
étudier le domaine de validité (pour chaque fonction trouvée, déterminer le plus grand intervalle contenant \(t_0\)).
2.1 Intervalle de Validité et Solution Maximale
En règle générale, lorsqu’une équation différentielle est munie d’une condition initiale \(y(t_0) = y_0\), nous recherchons un intervalle \(I\) qui contient \(t_0\), sur lequel une solution existe, et qui soit le plus grand possible. Ce domaine est appelé l’intervalle de validité de la solution. Une solution définie sur cet intervalle le plus large possible est appelée solution maximale.
Exemple: existence et unicité sur \(\mathbb{R}\)
Considérons \(\varphi(t,y) = 3t - 3y\) et \(y_0=\alpha\). La solution est:
Dans cet exemple, il existe une et une seule solution définie sur \(\mathbb{R}\).
Dans cet exemple, il existe une et une seule solution définie sur \(\mathbb{R}\). Les choses ne se passent pas toujours si bien. Les exemples ci-dessous montrent que l’étude mathématique de l’existence et de l’unicité des solutions d’un problème de Cauchy peut être une affaire délicate.
Exemple: existence sur un intervalle fini
Pour \(\varphi(t,y) = (y(t))^3\) et \(y_0 = 1\), la solution est:
\( y(t) = \frac{1}{\sqrt{1 - 2t}} \)
Cette solution est définie seulement pour \(t<\frac{1}{2}\). Cet exemple montre qu’un problème de Cauchy n’a pas toujours une solution pour tout \(t\in[0;+\infty[\) puisqu’ici la solution explose lorsque \(t\) tend vers la valeur \(1/2\) (en effet, nous avons \(\lim_{t\to(1/2)^-}y(t)=+\infty\)) : le graphe de la solution a une asymptote verticale en \(t=1/2\). On parle d’explosion de la solution en temps fini ou encore de barrière.
Cet exemple illustre un phénomène général : pour une solution d’une EDO, l’unique manière de ne pas être définie sur l’ensemble des réels \(\mathbb{R}\) est de présenter une asymptote verticale.
Exemple: non unicité
On se donne \(\varphi(t,y(t))=\sqrt[3]{y(t)}\) et \(y_0=0\). On cherche une fonction \(y\colon t\in\mathbb{R}^+\mapsto y(t)\in\mathbb{R}\) qui satisfait :
On vérifie que les trois fonctions \(y_1(t)=0\) et \(y_{2,3}(t)=\pm\sqrt{8t^3/27}\), pour tout \(t\ge0\), sont solutions du problème de Cauchy donné.
Cet exemple montre qu’un problème de Cauchy n’a pas nécessairement de solution unique (dans cet exemple, il y en a trois).
Exemple: infinité de solutions
On se donne \(\varphi(t,y(t))=|y(t)|^\alpha\) avec \(\alpha\in]0;1[\) et \(y_0=0\). On cherche une fonction \(y\colon t\in\mathbb{R}^+\mapsto y(t)\in\mathbb{R}\) qui satisfait :
Notons que pour \(\alpha\ge1\), le problème de Cauchy donné admet une et une seule solution, la fonction \(y(t)=0\) pour tout \(t\in\mathbb{R}^+\).
Dans ce cours, nous étudierons uniquement des problèmes de Cauchy ayant une unique solution sur l’intervalle indiqué.
3 Méthodes de Résolution
Seules les équations différentielles les plus simples peuvent être résolues par des formules explicites. Cependant, certaines propriétés des solutions d’une équation différentielle donnée peuvent être déterminées sans trouver leur forme exacte. Si une solution analytique n’est pas disponible, la solution peut être approchée numériquement.
Dans cette partie nous allons montrer comment calculer la solution générale de trois types d’EDO d’ordre 1: les EDO à variables séparables, les EDO linéaires et les EDO de Bernoulli.
3.1 EDO du premier ordre à variables séparables
Lorsque l’équation est de la forme
\(
f(y(x))y'(x)=g(x)
\)
où \(f\) et \(g\) sont des fonctions données dont on connaît des primitives \(F\) et \(G\), on a
pour obtenir \(F(y)=G(x)+C\) et exprimer \(y\) en fonction de \(x\).
Exemple
On veut résoudre l’équation différentielle
\( y'(x)=xy(x) \)
sur des intervalles à préciser. Il s’agit d’une EDO du premier ordre à variables séparables :
Recherche des solutions constantes.
Si \(y(x)=A\) pour tout \(x\), alors \(y'(x)=0\) pour tout \(x\) et l’EDO devient \(0=xA\) pour tout \(x\). Par conséquent \(A=0\) : la fonction \(y(x)=0\) pour tout \(x\) est l’unique solution constante de l’EDO.
Recherche des solutions non constantes.
La fonction \(y(x)=0\) pour tout \(x\) étant solution, toute autre solution \(x\mapsto y(x)\) sera donc non nulle. On peut alors diviser l’EDO par \(y\) et procéder formellement comme suit :
où \(a\), \(b\) et \(g\) sont des fonctions données, continues sur un intervalle \(I \subset \mathbb{R}\). Pour la résolution, on se place sur un intervalle \(J \subset I\) tel que la fonction \(a\) ne s’annule pas sur \(J\).
Pour \(x\in \mathcal{D}_b \cap \mathcal{D}_g \cap \{x\in \mathcal{D}_a|a(x)\neq0\}\), toute solution \(y(x)\) de cette EDO peut être écrite soit comme somme de deux fonctions (\(y_H\) et \(y_P\)) soit comme produit de deux fonctions (\(u\) et \(v\)) :
\(y_H\) est la solution générale de l’EDO homogène associée, c’est-à-dire de l’EDO \(a(x)y'(x)+b(x)y(x)=0\) (qui est à variables séparables).
En effet, la fonction \(y(x)=0\) pour tout \(x\) étant solution, toute autre solution \(x\mapsto y(x)\) sera donc non nulle. On peut alors diviser l’EDO homogène associée par \(y\) et procéder formellement comme suit :
Cette solution particulière peut être une solution évidente, par exemple une solution constante.
Dans la quête d’une solution évidente (non constante), le principe de superposition peut être utile : soient \(a\) et \(b\) deux réels et \(g_1, g_2, \dots, g_n\) des applications continues sur un intervalle \(I\) de \(\mathbb{R}\).
Si \(y_k\) est une solution particulière de l’EDO \(a y'(x)+b y(x)=g_k(x)\) alors \(\sum_{k=1}^n y_k\) est une solution particulière de l’EDO \(a y'(x)+b y(x)=\sum_{k=1}^n g_k(x)\).
Si on ne trouve pas de solution particulière, on peut en chercher une par la méthode de Lagrange ou de variation de la constante.
Si \(y_1(x)\) est une solution non nulle de l’EDO homogène, on introduit une fonction auxiliaire inconnue \(B(x)\) telle que \(y(x) = B(x) y_1(x)\) soit solution de notre EDO.
On calcule alors \(y'(x)\) et on reporte \(y'(x)\) et \(y(x)\) dans notre EDO. On observe que \(K(x)\) disparaît, ce qui fournit une auto-vérification.
Il ne reste que \(B'(x)\), ce qui permet de calculer \(B(x)\) et donc \(y_P(x)\).
3.3 EDO de Bernoulli
Les équations différentielles de Bernoulli sont du premier ordre et de la forme
où \(u\), \(v\) et \(w\) sont des fonctions données, continues sur un intervalle \(I \subset \mathbb{R}\). Pour la résolution, on se place sur un intervalle \(J \subset I\) tel que la fonction \(u\) ne s’annule pas sur \(J\) et on définit une nouvelle fonction \(x \mapsto z(x) = (y(x))^{1-\alpha}\). L’EDO initiale est alors équivalente à l’EDO linéaire du premier ordre suivante :
Formellement\(z = y^{1-\alpha}\) implique d’une part \(y = z y^\alpha\) et d’autre part \(z' = (1-\alpha)y^{-\alpha}y'\), et donc \(y' = (1-\alpha) z' y^\alpha\).
Par conséquent, pour \(x \in \mathcal{D}_v \cap \mathcal{D}_w \cap \{x \in \mathcal{D}_u \mid u(x) \neq 0\}\), toute solution \(y\) s’écrit comme
\(
y(x) = [z(x)]^{1/(1-\alpha)}
\)
avec :
- \(z(x) = \underbrace{C e^{-A(x)}}_{y_H(x)} + \underbrace{B(x) e^{-A(x)}}_{y_P(x)}\),
- \(A(x)\) une primitive de \((1-\alpha) \frac{v(x)}{u(x)}\),
- \(B(x)\) une primitive de \((1-\alpha) \frac{w(x)}{u(x)} e^{A(x)}\).
Exemple
On se propose de résoudre l’équation différentielle
Il s’agit d’une équation différentielle de Bernoulli. Comme \(u(x) = 1\) pour tout \(x \in \mathbb{R}\), on cherche sa solution générale sur \(\mathbb{R}\).
---title: "Rappels"jupyter: python3---# Équations Différentielles Ordinaires (EDO)Les équations différentielles décrivent l'évolution de divers phénomènes dans de nombreux domaines. Elles expriment des relations impliquant une ou plusieurs dérivées d'une fonction inconnue. Lorsque ces dérivées sont toutes prises par rapport à une seule variable, on parle d'équation différentielle ordinaire (EDO), tandis que celles impliquant des dérivées partielles sont qualifiées d'équations aux dérivées partielles (EDP).## EDO d'ordre $p$Une EDO se présente sous la forme générale:\( F(y(t),y'(t),y''(t),\dots,y^{(p)}(t))=g(t). \)- Les inconnues sont une **fonction** $y\colon I\subset\mathbb{R}\to\mathbb{R}$ et son **intervalle de définition** $I$.- Elle combine la fonction inconnue $y$ et ses dérivées $y'$, $y''$, \dots ,$y^{(p)}$ (où $p$ est l'**ordre** de l'équation).Si la fonction $g$, appelée "second membre" de l'équation, est nulle, l'équation est dite **homogène**.**Résoudre une équation différentielle** consiste à trouver toutes les fonctions définies sur un intervalle $I\subset\mathbb{R}$ qui vérifient cette équation (on dit aussi *intégrer* l'équation différentielle).Par le terme **solution générale** d'une EDO on désigne un représentant qui englobe l'ensemble des solutions possibles. L'une des solutions de l'EDO sera appelée *solution particulière*. On appelle *courbes intégrales* d'une EDO les courbes représentatives des solutions de l'équation.::: {.callout-caution collapse="true" title="Exemple"}La résolution de l'équation différentielle $y'(t)=-y(t)$ consiste à trouver toutes les fonctions $y(t)$ telles que $y'(t)=-y(t)$ pour tout $t\in I$. On peut vérifier que $y(t)=ce^{-t}$ pour tout $t\in\mathbb{R}$ (où $c$ est une constante réelle arbitraire) est une solution de l'EDO. En particulier, pour $c=0$, on obtient la solution nulle.:::### Représentations graphiques poir une EDO d'ordre 1 : champ de vecteurs et lignes de courantBien qu’il soit très rare que l’on puisse résoudre explicitement une équation différentielle donnée, comprendre l'allure des solutions peut être facilité en examinant le champ de vecteurs correspondant. Les graphes des solutions d'une équation différentielle $y'(t)=\varphi(t,y(t))$ sont, par définition, tangents à leur vecteur vitesse $(1,y'(t))$, donc au vecteur dérivé $(1, \varphi(t,y(t))$. Même sans connaître explicitement les solutions, connaître la fonction en chaque point permet de représenter ces vecteurs tangents. En traçant un grand nombre de ces vecteurs uniformément répartis dans le plan, on obtient le champ de vecteurs associé à l'équation différentielle. Cette représentation permet souvent de deviner les graphes des solutions, ces courbes étant tangentes en tous leurs points aux vecteurs du champ.- La fonction `quiver` du module `matplt.plotlib` permet de tracer un champ de vecteurs:`quiver(x_pos, y_pos, x_dir, y_dir, color)`- La fonction `streamplt.plot` permet de tracer des lignes de courant représentant un champ vectoriel. Utilisons-les pour obtenir les tracés associés à l'équation différentielle de notre exemple.Cf. <https://matplotlib.org/stable/api/_as_gen/matplotlib.pyplot.quiver.html> et <https://matplotlib.org/stable/api/_as_gen/matplotlib.pyplot.streamplot.html>```{python}# On représente en général un champ de vecteurs en des points régulièrement espacés de $ I\times\mathbb{R} $ et en normalisant les vecteurs. # Dessinons alors, en chaque point (t,y) de la grille un vecteur $\mathbf{V}_{t,y}$ de pente $\varphi(t,y)$ : le graphe de $f$ est tangent en chaque point $(t,y)$ au vecteur $\mathbf{V}_{t,y}$. # Remarquer qu'**on n'a pas besoin d'avoir résolu l'équation (analytiquement) pour pouvoir dessiner le champ de tangentes, et ceci permet parfois d'avoir une idée du comportement des solutions.**import numpy as npimport matplotlib.pyplot as pltphi =lambda t,y : -yg1 = np.linspace(0,4,21)g2 = np.linspace(-5,5,21)T,Y = np.meshgrid(g1,g2) # compute direction at each pointDT, DY =1, phi(T,Y) # compute growth rate on the plt.grid# M = np.sqrt(DT**2+DY**2) # norm growth rate M = np.hypot(DT,DY)plt.figure(figsize=(10,3))# Champ des pentesplt.subplot(1,2,1)# plt.quiver(T,Y, DT/M, DY/M, M, pivot='mid')plt.quiver(T,Y, DT/M, DY/M, M, cmap = plt.cm.viridis, scale_units='xy',scale=3.)plt.grid()plt.xlabel('t')plt.ylabel('y')plt.title('Champ des pentes');# Lignes de courantplt.subplot(1,2,2)# plt.streamplot(T,Y, DT/M, DY/M, color=M)plt.streamplot(T,Y, DT/M, DY/M, color=M, linewidth=1, cmap=plt.cm.viridis, density=2, arrowstyle='->', arrowsize=1.5)plt.grid()plt.xlabel('t')plt.ylabel('y')plt.title('Lignes de courant')plt.show();```## EDO d'ordre supérieur à 1 $\leadsto$ Système d'EDOs d'ordre 1Une EDO d'ordre $p$ est dite *normalisée* lorsqu'elle est exprimée sous la forme:\( y^{(p)}(t)=f(g(t),y(t),y'(t),y''(t),\dots,y^{(p-1)}(t)). \)Toute EDO normalisée d'ordre $p$ peut être transformée en un système de $p$ EDO d'ordre 1 de la manière suivante:\(\begin{cases}z_1'(t)=z_2(t),\\\dots\\z_{p-1}'(t)=z_p(t),\\z_p'(t)=f(g(t),z_1(t),z_2(t),\dots,z_{p-1}(t)).\end{cases}\)::: {.callout-caution collapse="true" title="Exemple"}Considérons l'équation différentielle d'ordre 2 suivante:\( y''(t)+ay'(t)+by(t)+c=0 \)Introduisons les deux fonctions $z_1(t)=y(t)$ et $z_2(t)=y'(t)$. On obtient alors le système:\(\begin{cases}z_1'(t)=z_2(t),\\z_2'(t)=-az_2(t)-bz_1(t)-c.\end{cases}\):::### Représentations graphiques pour un système de 2 EDO d'ordre 1 : portait de phaseTO DO## Conditions InitialesLes EDO ont généralement une infinité de solutions. Pour déterminer la solution appropriée qui représente le problème physique, il est nécessaire de prendre en compte des données supplémentaires.::: {.callout-tip title="Définition"}Soit une EDO d'ordre $p$. Une condition initiale (CI) est un ensemble de relations du type:\( y(t_0)=y_0, \quad y'(t_0)=y'_0, \dots, \quad y^{(p-1)}(t_0)=y^{(p-1)}_0 \)qui imposent en $t_0$ les valeurs respectives de la fonction inconnue et de ses dérivées.:::# Problème de CauchyLe problème associé à une EDO avec une condition initiale est connu sous le nom de *problème de Cauchy*:::: {.callout-tip title="Définition: Problème de Cauchy"}Considérons un intervalle $I\subset\mathbb{R}$, un point $t_0$ dans $I$, une fonction $\varphi \colon I \times \mathbb{R} \to \mathbb{R}$ continue. Le *problème de Cauchy* est défini comme la recherche d'une fonction réelle $y\in\mathcal{C}^1(I)$ telle que\(\begin{cases}y'(t) = \varphi(t,y(t)), &\forall t \in I,\\y(t_0) = y_0.\end{cases}\)avec $y_0$ une valeur donnée appelée \emph{condition initiale}.:::<!-- Si $\varphi$ ne dépend pas explicitement de $t$, l'EDO est dite *autonome*. -->Nous concentrerons notre analyse principalement sur le cas où une seule EDO est présente, c'est-à-dire le cas scalaire. **Résoudre un problème de Cauchy**, c'est rechercher toutes les fonctions, définies sur un intervalle $I\subset\mathbb{R}$, qui satisfont l'équation différentielle tout en vérifiant la condition initiale. Cela soulève des questions naturelles telles que :- trouver toutes les fonctions solutions de l'EDO,- parmi ces fonctions, choisir celles qui respectent la CI (existence? unicité?),- étudier le domaine de validité (pour chaque fonction trouvée, déterminer le plus grand intervalle contenant $t_0$).## Intervalle de Validité et Solution MaximaleEn règle générale, lorsqu'une équation différentielle est munie d'une condition initiale $y(t_0) = y_0$, nous recherchons un intervalle $I$ qui contient $t_0$, sur lequel une solution existe, et qui soit *le plus grand possible*. Ce domaine est appelé l'*intervalle de validité* de la solution. Une solution définie sur cet intervalle le plus large possible est appelée *solution maximale*.::: {.callout-caution collapse="true" title="Exemple: existence et unicité sur $\mathbb{R}$"}Considérons $\varphi(t,y) = 3t - 3y$ et $y_0=\alpha$. La solution est:\( y(t) = (\alpha + \frac{1}{3})e^{-3t} + t - \frac{1}{3}. \)Dans cet exemple, il existe une et une seule solution définie sur $\mathbb{R}$. :::Dans cet exemple, il existe une et une seule solution définie sur $\mathbb{R}$. Les choses ne se passent pas toujours si bien. Les exemples ci-dessous montrent que l'étude mathématique de l'existence et de l'unicité des solutions d'un problème de Cauchy peut être une affaire délicate.::: {.callout-caution collapse="true" title="Exemple: existence sur un intervalle fini"}Pour $\varphi(t,y) = (y(t))^3$ et $y_0 = 1$, la solution est:\( y(t) = \frac{1}{\sqrt{1 - 2t}} \)Cette solution est définie seulement pour $t<\frac{1}{2}$. Cet exemple montre qu'*un problème de Cauchy n'a pas toujours une solution pour tout $t\in[0;+\infty[$* puisqu'ici la solution explose lorsque $t$ tend vers la valeur $1/2$ (en effet, nous avons $\lim_{t\to(1/2)^-}y(t)=+\infty$) : le graphe de la solution a une asymptote verticale en $t=1/2$. On parle d'*explosion de la solution en temps fini* ou encore de *barrière*.:::Cet exemple illustre un phénomène général : pour une solution d'une EDO, l'unique manière de ne pas être définie sur l'ensemble des réels $\mathbb{R}$ est de présenter une asymptote verticale.::: {.callout-caution collapse="true" title="Exemple: non unicité"}On se donne $\varphi(t,y(t))=\sqrt[3]{y(t)}$ et $y_0=0$. On cherche une fonction $y\colon t\in\mathbb{R}^+\mapsto y(t)\in\mathbb{R}$ qui satisfait :\(\begin{cases}y'(t) = \sqrt[3]{y(t)}, &\forall t>0,\\y(0) = 0.\end{cases}\)On vérifie que les trois fonctions $y_1(t)=0$ et $y_{2,3}(t)=\pm\sqrt{8t^3/27}$, pour tout $t\ge0$, sont solutions du problème de Cauchy donné.:::Cet exemple montre qu'*un problème de Cauchy n'a pas nécessairement de solution unique* (dans cet exemple, il y en a trois).::: {.callout-caution collapse="true" title="Exemple: infinité de solutions"}On se donne $\varphi(t,y(t))=|y(t)|^\alpha$ avec $\alpha\in]0;1[$ et $y_0=0$. On cherche une fonction $y\colon t\in\mathbb{R}^+\mapsto y(t)\in\mathbb{R}$ qui satisfait :\(\begin{cases}y'(t) = |y(t)|^\alpha, &\forall t>0,\\y(0) = 0.\end{cases}\)On vérifie que, pour tout $c\in\mathbb{R}^+$, les fonctions :\(y_c(t)=\begin{cases}(1-\alpha)^{1/(1-\alpha)} (x-c)^{1/(1-\alpha)} & \text{si } x\ge c,\\0 & \text{si } 0\le x\le c\end{cases}\)sont solutions du problème de Cauchy donné.Notons que pour $\alpha\ge1$, le problème de Cauchy donné admet une et une seule solution, la fonction $y(t)=0$ pour tout $t\in\mathbb{R}^+$.:::**Dans ce cours, nous étudierons uniquement des problèmes de Cauchy ayant une unique solution sur l'intervalle indiqué.**# Méthodes de RésolutionSeules les équations différentielles les plus simples peuvent être résolues par des **formules explicites**. Cependant, certaines **propriétés** des solutions d'une équation différentielle donnée peuvent être déterminées sans trouver leur forme exacte. Si une solution analytique n'est pas disponible, la solution peut être **approchée numériquement**. <div class="image-container">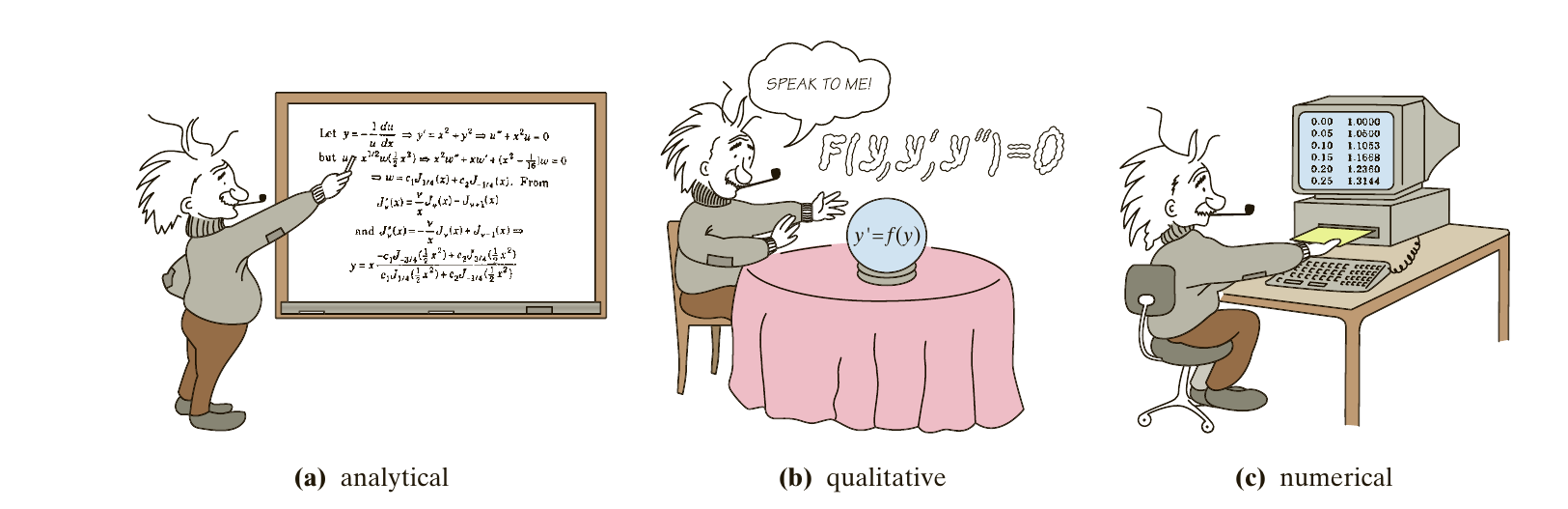{fig-align="center" width="100%"}</div>Dans cette partie nous allons montrer comment calculer la solution générale de trois types d'EDO d'ordre 1: les EDO à variables séparables, les EDO linéaires et les EDO de Bernoulli.## EDO du premier ordre à variables séparables Lorsque l'équation est de la forme \(f(y(x))y'(x)=g(x)\)où $f$ et $g$ sont des fonctions données dont on connaît des primitives $F$ et $G$, on a \(\underbrace{\int f(y(x))y'(x) \mathrm{d}x}_{=\int f(u)\mathrm{d}u=F(u)} = \underbrace{\int g(x)\mathrm{d}x}_{G(x)+C}\)donc \(F(y(x))= G(x) + C\qquad \text{où } C \in \mathbb{R},\)et, si $F$ possède une fonction réciproque $F^{-1}$, on en déduit \(y(x)=F^{-1}(G(x)+C),\)relation qui donne toutes les solutions de l'équation. Cette solution générale dépend de la constante d'intégration $C$. ::: {.callout-tip collapse="true" title="Astuce mnémotechnique"}En pratique, étant donné que $y'(x)=\mathrm{d}{y}/\mathrm{d}{x}$, on peut écrire l'équation $f(y(x))y'(x)=g(x)$ sous la forme \(f(y)\mathrm{d}y=g(x)\mathrm{d}x,\)puis intégrer formellement les deux membres \(\int f(y)\mathrm{d}y = \int g(x)\mathrm{d}x,\)pour obtenir $F(y)=G(x)+C$ et exprimer $y$ en fonction de $x$. :::::: {.callout-warning collapse="true" title="Exemple"}On veut résoudre l'équation différentielle \( y'(x)=xy(x) \)sur des intervalles à préciser. Il s'agit d'une EDO du premier ordre à variables séparables : - **Recherche des solutions constantes.** Si $y(x)=A$ pour tout $x$, alors $y'(x)=0$ pour tout $x$ et l'EDO devient $0=xA$ pour tout $x$. Par conséquent $A=0$ : la fonction $y(x)=0$ pour tout $x$ est l'unique solution constante de l'EDO. - **Recherche des solutions non constantes.** La fonction $y(x)=0$ pour tout $x$ étant solution, toute autre solution $x\mapsto y(x)$ sera donc non nulle. On peut alors diviser l'EDO par $y$ et procéder formellement comme suit : \(\begin{aligned}\frac{y'(x)}{y(x)}=x&\quad\implies\quad\frac{\frac{\mathrm{d}y}{\mathrm{d}x}}{y(x)}=x\\&\quad\implies\quad\frac{\mathrm{d}y}{y}=x\mathrm{d}x\\&\quad\implies\quad\int\frac{1}{y}\mathrm{d}y=\int x\mathrm{d}x\\&\quad\implies\quad\ln|y|=\frac{x^2}{2}+C\text{ avec }C\in\mathbb{R}.\end{aligned}\)Ainsi, toute solution non nulle est de la forme \(y(x)=De^{x^2/2} \qquad\text{avec }D\in\mathbb{R}^*. \):::## EDO linéaires du premier ordre Elles sont de la forme \(a(x)y'(x)+b(x)y(x)=g(x)\)où $a$, $b$ et $g$ sont des fonctions données, continues sur un intervalle $I \subset \mathbb{R}$. Pour la résolution, on se place sur un intervalle $J \subset I$ tel que la fonction $a$ ne s'annule pas sur $J$. Pour $x\in \mathcal{D}_b \cap \mathcal{D}_g \cap \{</span>x\in \mathcal{D}_a|a(x)\neq0\}$, toute solution $y(x)$ de cette EDO peut être écrite soit comme somme de deux fonctions ($y_H$ et $y_P$) soit comme produit de deux fonctions ($u$ et $v$) : \(y(x)=\underbrace{Ce^{-A(x)}}_{y_H(x)} + \underbrace{B(x)e^{-A(x)}}_{y_P(x)}\)avec - $A(x)$ une primitive de $\dfrac{b(x)}{a(x)}$, - $B(x)$ une primitive de $\dfrac{g(x)}{a(x)}e^{A(x)}$. ::: {.callout-note collapse="true" title="Vérification"}Pour vérifier que c'est bien une solution, il suffit de dériver : \(\begin{aligned}y'(x) &=CA'(x)e^{-A(x)}-B(x)A'(x)e^{-A(x)}+B'(x)e^{-A(x)} \\&=-A'(x)\left(Ce^{-A(x)}+B(x)e^{-A(x)}\right)+B'(x)e^{-A(x)} \\&=-A'(x)y(x)+B(x)e^{-A(x)} \\&=-\dfrac{b(x)}{a(x)} y(x)+\dfrac{g(x)}{a(x)}e^{A(x)}e^{-A(x)}=-\dfrac{b(x)}{a(x)} y(x)+\dfrac{g(x)}{a(x)}\end{aligned}\)donc $a(x)y'(x)=-b(x)y(x)+g(x)$. :::::: {.callout-warning collapse="true" title="Exemple"}Considérons l'EDO \(y'(x)-y(x)=x.\)On a \(\begin{aligned} a(x) &= 1, \\ b(x) &= -1, \\ g(x) &= x.\end{aligned}\)Pour $x \in \mathbb{R}$, on a - $A(x) = \int -1 \mathrm{d}x = -x$, - $B(x) = \int x e^{-x} \mathrm{d}x = -(1 + x)e^{-x}$, d'où \(y(x) = \left( C - (1 + x)e^{-x} \right)e^{x} = Ce^{x} - (1 + x).\):::::: {.callout-tip collapse="true" title="Remarque"}On peut montrer que : - **$y_H$ est la solution générale de l'EDO homogène associée**, c'est-à-dire de l'EDO $a(x)y'(x)+b(x)y(x)=0$ (qui est à variables séparables). En effet, la fonction $y(x)=0$ pour tout $x$ étant solution, toute autre solution $x\mapsto y(x)$ sera donc non nulle. On peut alors diviser l'EDO homogène associée par $y$ et procéder formellement comme suit : \( \begin{aligned} \frac{y'(x)}{y(x)}=-\frac{b(x)}{a(x)} &\quad\implies\quad \int\frac{1}{y}\mathrm{d}y=-\int -\frac{b(x)}{a(x)}\mathrm{d}x\\ &\quad\implies\quad \ln|y|=-\int\frac{b(x)}{a(x)}\mathrm{d}x . \end{aligned} \) Ainsi, toute solution non nulle de l'équation homogène associée est de la forme \( y_H(x)=C e^{-A(x)}\qquad\text{où } A(x)=\int \frac{b(u)}{a(u)}\mathrm{d}u \) avec $C$ constante arbitraire. - **$y_P$ est une solution particulière.** Cette solution particulière peut être une solution *évidente*, par exemple une solution constante. Dans la quête d'une solution évidente (non constante), le *principe de superposition* peut être utile : soient $a$ et $b$ deux réels et $g_1, g_2, \dots, g_n$ des applications continues sur un intervalle $I$ de $\mathbb{R}$. Si $y_k$ est une solution particulière de l'EDO $a y'(x)+b y(x)=g_k(x)$ alors $\sum_{k=1}^n y_k$ est une solution particulière de l'EDO $a y'(x)+b y(x)=\sum_{k=1}^n g_k(x)$. Si on ne trouve pas de solution particulière, on peut en chercher une par la **méthode de Lagrange** ou **de variation de la constante**. Si $y_1(x)$ est une solution non nulle de l'EDO homogène, on introduit une fonction auxiliaire inconnue $B(x)$ telle que $y(x) = B(x) y_1(x)$ soit solution de notre EDO. On calcule alors $y'(x)$ et on reporte $y'(x)$ et $y(x)$ dans notre EDO. On observe que $K(x)$ disparaît, ce qui fournit une auto-vérification. Il ne reste que $B'(x)$, ce qui permet de calculer $B(x)$ et donc $y_P(x)$. :::## EDO de BernoulliLes équations différentielles de Bernoulli sont du premier ordre et de la forme\(u(x)y'(x) + v(x)y(x) = w(x)(y(x))^\alpha, \quad \alpha \in \mathbb{R} \setminus \{</span>0, 1<span class="sc">\}\)où $u$, $v$ et $w$ sont des fonctions données, continues sur un intervalle $I \subset \mathbb{R}$. Pour la résolution, on se place sur un intervalle $J \subset I$ tel que la fonction $u$ ne s'annule pas sur $J$ et on définit une nouvelle fonction $x \mapsto z(x) = (y(x))^{1-\alpha}$. L'EDO initiale est alors équivalente à l'EDO linéaire du premier ordre suivante : *Formellement* $z = y^{1-\alpha}$ implique d'une part $y = z y^\alpha$ et d'autre part $z' = (1-\alpha)y^{-\alpha}y'$, et donc $y' = (1-\alpha) z' y^\alpha$.\(\underbrace{u(x)}_{a(x)} z'(x) + \underbrace{(1-\alpha) v(x)}_{b(x)} z(x) = \underbrace{(1-\alpha) w(x)}_{g(x)}.\)Par conséquent, pour $x \in \mathcal{D}_v \cap \mathcal{D}_w \cap \{</span>x \in \mathcal{D}_u \mid u(x) \neq 0\}$, toute solution $y$ s'écrit comme \(y(x) = [z(x)]^{1/(1-\alpha)} \)avec : - $z(x) = \underbrace{C e^{-A(x)}}_{y_H(x)} + \underbrace{B(x) e^{-A(x)}}_{y_P(x)}$, - $A(x)$ une primitive de $(1-\alpha) \frac{v(x)}{u(x)}$, - $B(x)$ une primitive de $(1-\alpha) \frac{w(x)}{u(x)} e^{A(x)}$.::: {.callout-warning collapse="true" title="Exemple"}On se propose de résoudre l'équation différentielle \(y'(x) + \frac{1}{2}y(x) = \frac{1}{2}(x-1)y^3(x).\)Il s'agit d'une équation différentielle de Bernoulli. Comme $u(x) = 1$ pour tout $x \in \mathbb{R}$, on cherche sa solution générale sur $\mathbb{R}$. - $A(x) = (1-\alpha) \int \frac{v(x)}{u(x)} \, \mathrm{d}x = -2 \int \frac{1/2}{1} \, \mathrm{d}x = -x$, - $B(x) = (1-\alpha) \int \frac{w(x)}{u(x)} e^{A(x)} \mathrm{d}x$ $= -2 \int \frac{(x-1)/2}{1} e^{-x} \mathrm{d}x$ $= \int (1-x) e^{-x} \mathrm{d}x$ $= -(1-x) e^{-x} - \int e^{-x} \mathrm{d}x = x e^{-x}$, - $z(x) = \left( C + B(x) \right) e^{-A(x)} = (C + x e^{-x}) e^x = C e^x + x$. On conclut que la solution générale de l'EDO de Bernoulli assignée est \(y(x) = \frac{1}{\sqrt{x + C e^x}}.\)Notons que $y$ n'est définie que si $x + C e^x > 0$.:::