CM 5 - Convergence et A-stabilité des schémas 👣 multipas 👣 linéaires

Auteur·rice

Gloria FACCANONI

Date de publication

10 mars 2025

Code

%reset -f

from IPython.display import display, Math, Latex, Markdown

import sympy as sp
sp.init_printing() 

import matplotlib.pyplot as plt
plt.rcParams.update({<span class="st">'font.size'</span>: <span class="dv">16</span>})
import numpy as np

1 Rappels

Considérons le problème de Cauchy dont on suppose qu’il admet une solution unique $y(t)$ sur un intervalle $I=[t_0,T]$ :

$\begin{cases} y'(t) = \varphi(t,y(t)), &\forall t \in I=[t_0,T],\\ y(t_0) = y_0, \end{cases}$

Définition.

Notons

$ \varphi_{n-j} \stackrel{\text{def}}{=} \varphi(t_{n-j},u_{n-j}). $

Soit $p\ge0$ un entier et posons $q=p+1$.
On se donne les coefficients $\{a_j\}_{j=0}^p$ et $\{b_j\}_{j=-1}^p$ (il y en a $2q+1$ en tout).

Une méthode multipas linéaire (qu’on appellera simplement multipas, ou multistep) à $q$ étapes (=pas) s’écrit sous la forme générale d’une combinaison linéaire de valeurs de la solution approchée $u$ et de la fonction $\varphi$ en des points de la grille de temps :

$ \begin{aligned} u_{n+1} &= \sum_{j=0}^p a_ju_{n-j} + h\sum_{j=-1}^p b_j\varphi(t_{n-j},u_{n-j}) \\ &= \sum_{j=0}^p \Big(a_ju_{n-j} + b_j\varphi(t_{n-j},u_{n-j}) \Big) + hb_{-1}\varphi(t_{n+1},u_{n+1}), \end{aligned} \qquad n=p,p+1,\dots,N-1. $

1.1 Remarques

Explicite vs Implicte Si $b_{-1}=0$ la méthode est explicite, sinon implicite.
Initialisation Les données initiales $u_0, u_1, \dots, u_p$ doivent être fournies. Mis à part $u_0$, qui est égale à $y_0$ connu, les autres valeurs, $u_1, \dots, u_p$ doivent être obtenues à l’aide d’autres méthodes d’approximation qui doivent être suffisamment précises. Pour les tests de convergence, pour lesquels on connaît la solution exacte, on utilisera la solution exacte pour calculer ces valeurs initiales.

1.2 Les méthodes que nous avons vues jusqu’à présent sont des méthodes multipas ?

Les trois méthodes classiques suivantes sont des méthodes à $q=1$ pas ($p=0$), car elles sont toutes de la forme

$ u_{n+1} = a_0 u_n + h b_0 \varphi(t_n,u_n) + h b_{-1} \varphi(t_{n+1},u_{n+1}) $

Méthode	Formule	$a_0$	$b_{-1}$	$b_0$
Euler explicite	$u_{n+1}=u_n+h\varphi(t_n,u_n)$	1	0	1
Euler implicite	$u_{n+1}=u_n+h\varphi(t_{n+1},u_{n+1})$	1	1	0
Crank-Nicolson	$u_{n+1}=u_n+\frac{h}{2}(\varphi(t_n,u_n)+\varphi(t_{n+1},u_{n+1}))$	1	$\frac{1}{2}$	$\frac{1}{2}$

Les méthodes Adams-Bashforth $\text{AB}_q$ et Adams-Moulton $\text{AM}_q$, Nyström $\text{N}_q$, Milne-Simpson $\text{MS}_q$ et BDF $\text{BFD}_q$ sont des méthodes multipas à $q=p+1$ étapes (=pas) linéaires.
Les méthodes Euler modifié et Heun ne sont pas des méthodes multipas : elles sont des méthodes de la famille Runge-Kutta dont on verra la définition plus tard.

🔴 Théorème d’équivalence de Lax-Ritchmyer : consistance + zéro-stabilité = convergence

Un schéma consistant est convergent ssi il est zéro-stable.

La convergence étudie la résolution du problème de Cauchy sur des intervalles bornés. Dans ce contexte, le nombre $N$ de sous-intervalles ne tend vers l’infini que lorsque $h$ tend vers zéro.
Cependant, il existe de nombreuses situations où le problème de Cauchy doit être résolu sur des intervalles de temps très longs, voire infinis. Dans ces cas-là, même pour un $h$ fixé, $N$ tend vers l’infini, rendant la notion de zéro-stabilité inapplicable puisque $T - t_0 \to +\infty$.
On cherche donc des méthodes capables d’approcher la solution sur des intervalles de temps arbitrairement grands, y compris avec des pas de temps $h$ relativement grands.

Définition : A-stabilité dans $\mathbb{R}$

Soit $\beta > 0$ un réel positif et considérons le problème de Cauchy (modèle simplifié = toy-model) :

$\begin{cases} y'(t) = -\beta y(t), &\text{pour } t > 0, \\ y(0) = y_0 \end{cases}$

où $y_0 \neq 0$ est une valeur initiale donnée. La solution exacte est $y(t) = y_0 e^{-\beta t}$, d’où :

$\lim_{t \to +\infty} y(t) = 0.$

Considérons un pas de temps fixé $h > 0$ et définissons $t_n = nh$ pour $n \in \mathbb{N}$. Notons $u_n \approx y(t_n)$ une approximation de la solution $y$ au temps $t_n$.
Si, sous d’éventuelles conditions sur $h$, on a

$ \lim_{n \to +\infty} u_n = 0, $

alors on dit que le schéma est A-stable (ou absolument stable).

2 Polynômes caractéristiques

Dans ce chapitre nous allons étudier d’abord la convergence (à travers les notions de consistance et de zéro-stabilité) puis la A-stabilité d’une méthode multistep.

Dans l’analyse de ces méthodes, trois polynômes jouent un rôle clé. Pour cela, commençons par réécrire le schéma multistep comme suit:

$ u_{n+1} -\sum_{j=0}^p a_ju_{n-j}= h\left(\sum_{j=0}^p b_j\varphi(t_{n-j},u_{n-j})+b_{-1}\varphi(t_{n+1},u_{n+1})\right). $

Définition.

Pour $r\in\mathbb{C}$, on associe à une méthode numérique linéaire multipas les trois polynômes caractéristiques suivants :

premier polynôme caractéristique

$ \varrho(r)=r^{p+1}-\sum_{j=0}^p a_jr^{p-j} $

second polynôme caractéristique

$ \sigma(r)=b_{-1}r^{p+1}+\sum_{j=0}^p b_jr^{p-j} $

polynôme de A-stabilité

$ p_z(r) = \varrho(r) - z \sigma(r) $

Formellement,

pour construire le premier polynôme caractéristique on ne regarde que le LHS et les $u_{n-j}$ deviennent des $r^{p-j}$,
pour construire le second polynôme caractéristique on ne regarde que le RHS divisé par $h$ et les $\varphi(t_{n-j},u_{n-j})$ deviennent des $r^{p-j}$.

On verra que les racines du polynôme $\varrho$ sont liées à la zéro-stabilité tandis que celles du polynôme $p$ sont liées à la stabilité absolue (en association avec un choix particulier de $z=h\lambda$).

Exemple : méthodes classiques à $q=1$ pas :

Méthode	Formule	$a_0$	$b_{-1}$	$b_0$	$\varrho(r)$	$\sigma(r)$
Euler explicite	$u_{n+1}=u_n+h\varphi(t_n,u_n)$	1	0	1	$r-1$	$1$
Euler implicite	$u_{n+1}=u_n+h\varphi(t_{n+1},u_{n+1})$	1	1	0	$r-1$	$r$
Crank-Nicolson	$u_{n+1}=u_n+\frac{h}{2}(\varphi(t_n,u_n)+\varphi(t_{n+1},u_{n+1}))$	1	$\frac{1}{2}$	$\frac{1}{2}$	$r-1$	$\frac{1}{2}r+\frac{1}{2}$

Exemple : méthodes à $q>1$ pas :

Méthode	$p$	$\varrho(r)$	$\sigma(r)$
$\text{AB}_q$ ou $\text{AM}_q$	$q-1$	$r^{q+1}-r^{q}=r^{q}(r-1)$	-
$\text{N}_q$ ou $\text{MS}_q$	$q-1$	$r^{q+1}-r^{q-1}=r^{q-1}(r^2-1)$	-
$\text{BDF}_2$	$q-1$	$(r-1)\left(r-\frac{1}{3}\right)$	$\frac{2}{3}$

3 Convergence d’un schéma multipas linéaire

🔴 Théorème (Dahlquist 1956)

Une méthode linéaire multipas est convergente si et seulement si elle est

1️⃣ consistante et
2️⃣ (zero)-stable.

La convergence est d’ordre $\omega$ si la méthode est convergente et, de plus, consistante d’ordre $\omega$.

3.1 1️⃣ Consistance

Une méthode est dite consistante (ou consistante d’ordre au moins 1) si l’erreur de troncature $\tau(h)=\max_n |\tau_n(h)|$ tend vers zéro quand $h$ tend vers zéro, où $\tau_n(h)$ est l’erreur de troncature locale de la méthode multi-pas définie par

$ \tau_n(h)=\frac{1}{h}\left(y_{n+1}-\sum_{j=0}^p a_jy_{n-j}-h\sum_{j=0}^p b_j\varphi(t_{n-j},y_{n-j})-hb_{-1}\varphi(t_{n+1},y_{n+1})\right). $

Si, de plus, $\tau(h)=\mathscr{O}(Ch^\omega)$, on dit que la méthode est consistante d’ordre $\omega$.

Pour évaluer la consistance et son ordre, nous allons introduire une nouvelle quantité $\xi(i)$.

Définition.

Pour $i=0,1,\dots$ introduisons la quantité

$ \xi(i) = \sum_{j=0}^p (-j)^{i}a_j+i\sum_{j=-1}^p (-j)^{i-1}b_j, $

ayant posé $(-j)^0=1$ même pour $j=0$.

Pour bien comprendre cette définition, on peut écrire les premières valeurs de $\xi(i)$ :

$ \begin{aligned} \xi(0) &= \sum_{j=0}^p a_j, \\ \xi(1) &= \sum_{j=0}^p -j a_j + \sum_{j=-1}^p b_j, \\ \xi(2) &= \sum_{j=0}^p j^{2} a_j + 2 \sum_{j=-1}^p -j b_j, \\ \xi(3) &= \sum_{j=0}^p (-j)^{3} a_j + 3 \sum_{j=-1}^p j^{2} b_j, \\ &\quad \vdots \end{aligned} $

Exemple avec un schéma à $q=4$ pas (et donc $p=3$) :

$\xi(0)=\Big(a_0+a_1+a_2+a_3\Big)$
$\xi(1)=-\Big(a_1+2a_2+3a_3\Big)+b_{-1}+\Big(b_1+b_2+b_3\Big)$
$\xi(2)=\Big(a_1+4a_2+9a_3\Big)+2b_{-1}-2\Big(b_1+2b_2+3b_3\Big)$
$\xi(3)=-\Big(a_1+8a_2+27a_3\Big)+3b_{-1}+3\Big(b_1+4b_2+9b_3\Big)$

Il n’y a pas de difficulté à calculer ces quantités pour un schéma donné, cependant il faut faire attention à ne pas se tromper dans les calculs, notamment les signes des termes. Pour vous aider, voici un petit script Python qui calcule ces quantités de façon automatique pour un schéma donné. Il suffit de rentrer les valeurs de $p$ et jusqu’à quel ordre vous voulez calculer les $\xi(i)$.

Code

# =============================================================================
# Calcul et affichage de xi(i) pour un i donné pour un schema de pas q=p+1
# ============================================================================= 
def xi(i,p):
    q = p+1
    aa = sp.symbols(f'a_0:{</span>q<span class="sc">}')
    bb = sp.symbols(f'b_0:{</span>q<span class="sc">}')
    bm1 = sp.Symbol('b_{-1}')
    p = len(aa)
    sa = sum( [ (-j)**i * aa[j] for j in range(p) ] )
    sb = bm1+sum( [(-j)**(i-1) * bb[j] for j in range(1,p)] )
    # ??? si j=0 et i=0, il calcule (-j)**i =1 et on a bien a_0 dans la somme
    # mais si j=0 et i=1 il ne calcule pas b_0 et il faut l'ajouter à la main
    if i==1:
        sb += bb[0]
    xi_rhs  = (sa).factor()+(i*sb).factor()                  # calcul de xi(i)
    display(Markdown(f"$\\xi({</span>i<span class="sc">}) = {</span>sp<span class="sc">.</span>latex(xi_rhs)<span class="sc">}$") )  # affichage de xi(i)
    # return xi_rhs                                            # retourne xi(i) mais on ne s'en sert pas pour l'instant

# =============================================================================
# Calcul et affichage des xi(i) pour i=0,...,omega
# =============================================================================
def xi_cond(p,omega):
    # j = 0...p # coeffs du schema
    # i = 0, ..., omega ordre du schema
    q = p+1
    display(Markdown(f"**Pour ${</span>p<span class="op">=</span><span class="sc">}$, on a une méthode à $q={</span>p<span class="op">+</span><span class="dv">1</span><span class="sc">}$ pas et on affiche $ξ(i)$ pour $i=0,...,{</span>omega<span class="sc">}$**"))
    for i in range(omega+1):
        xi(i,p)
    

# =============================================================================    
# Exemple d'utilisation
# Calcul des xi(i) pour i=0,...,omega
# =============================================================================
xi_cond(p=1,omega=5)

Pour $p=1$, on a une méthode à $q=2$ pas et on affiche $ξ(i)$ pour $i=0,...,5$

$\xi(0) = a_{0} + a_{1}$

$\xi(1) = - a_{1} + b_{0} + b_{1} + b_{-1}$

$\xi(2) = a_{1} - 2 \left(b_{1} - b_{-1}\right)$

$\xi(3) = - a_{1} + 3 \left(b_{1} + b_{-1}\right)$

$\xi(4) = a_{1} - 4 \left(b_{1} - b_{-1}\right)$

$\xi(5) = - a_{1} + 5 \left(b_{1} + b_{-1}\right)$

La proposition suivante donne une condition nécessaire et suffisante pour la consistance d’une méthode multipas.
Par un développement de Taylor (assez fastidieux), on peut montrer que :

🔴 Proposition [consistance et ordre de consistance]

La méthode est consistante (ou, plus précisément, consistante d’ordre au moins 1) ssi $\xi(0)=\xi(1)=1$.

La méthode est consistante d’ordre $\omega\ge2$ ssi $\xi(0)=\xi(1)=\dots=\xi(\omega)=1$.

Remarques :

La condition de consistance d’ordre au moins 1 est une condition nécessaire pour la convergence d’une méthode numérique. En particulier, on peut noter que :
- la condition $\xi(0)=1$ équivaut à $\varrho(1)=0$,
- la condition $\xi(1)=1$ équivaut à $\varrho'(1)=\sigma(1)$.
La condition de consistance d’ordre $\omega$ signifie que toutes les valeurs de $\xi(i)$ sont égales à 1 pour $i$ allant de 0 à $\omega$, et non pas seulement $\xi(\omega)$.

Exemple : étudier la consistance et l’ordre de consistance du schéma multipas linéaire $\text{AB}_2$

$ u_{n+1} = u_n + \frac{h}{2} \left( 3\varphi_n - \varphi_{n-1} \right) $

$p=1$ $\leadsto$ $q=2$ : c’est un schéma de la forme

$ u_{n+1}= \underset{= \, 1}{a_0} u_n + \underset{= \, 0}{a_1} u_{n-1} + h \left( \underset{= \, \frac{3}{2}}{b_0} \varphi_n + \underset{= \, -\frac{1}{2}}{b_1} \varphi_{n-1} \right) + h \underset{= \, 0}{b_{-1}} \varphi_{n+1} $

Notons que $b_{-1}=0$ $\leadsto$ le schéma est explicite.

On vérifie la consistance en calculant les premières deux valeurs de $ (i) $. Pour afficher $\xi(0)$ et $\xi(1)$ dans le cas général, on peut utiliser la fonction précédente :

Code

xi_cond(p=1,omega=1)

Pour $p=1$, on a une méthode à $q=2$ pas et on affiche $ξ(i)$ pour $i=0,...,1$

$\xi(0) = a_{0} + a_{1}$

$\xi(1) = - a_{1} + b_{0} + b_{1} + b_{-1}$

Maintenant on remplace les valeurs des coefficients dans les formules de $\xi(i)$ pour obtenir les valeurs de $\xi(0)$ et $\xi(1)$.

$\begin{aligned} \xi(0) &= 1 + 0 = 1 \\ \xi(1) &= -0+\frac{3}{2}-\frac{1}{2}+0 = 1 \end{aligned}$

Le schéma est consistante, c’est à dire qu’il est d’ordre au moins 1.

Pour vérifier si le schéma est consistant d’ordre 2, on doit calculer $\xi(2)$ et vérifier si $\xi(2)=1$. Pour cela, affichons $\xi(i)$ pour $i=2$ dans le cas général :

Code

xi(i=2,p=1) # xi(2) avec p=1

$\xi(2) = a_{1} - 2 \left(b_{1} - b_{-1}\right)$

On évalue alors $\xi(2)$ :

$ \xi(2) = 0 - 2\left(-\frac{1}{2}-0\right) = 1 $

donc le schéma est consistant d’ordre au moins 2.

Pour vérifier si le schéma est consistant d’ordre au moins 3, on doit calculer $\xi(3)$ et vérifier si $\xi(3)=1$. Pour cela, affichons $\xi(i)$ pour $i=3$ dans le cas général :

Code

xi(i=3,p=1) # xi(3) avec p=1

$\xi(3) = - a_{1} + 3 \left(b_{1} + b_{-1}\right)$

On évalue alors $\xi(3)$ :

$ \xi(3) = 0 + 3\left(-\frac{1}{2}+0\right) \neq 1 $

donc le schéma n’et pas d’ordre 3. On conclut qu’il est consistant d’ordre exactement 2.

3.2 2️⃣ Zéro-stabilité

🔴 Proposition [zéro-stabilité et condition des racines]

Soient $r_0, r_1,\dots, r_p$ les $p+1$ racines (dans $\mathbb{C}$) du premier polynôme caractéristique $\varrho(r)=r^{p+1}-\sum_{j=0}^p a_jr^{p-j}$.
La méthode est zéro-stable ssi

$ \begin{cases} |r_j|\le1 \quad\text{pour tout }j=0,\dots,p \\ r_j\text{ a multiplicité}>1\quad\implies \quad |r_j|<1. \end{cases} $

Explication :

La première condition signifie que, dans le plan complexe, toutes les racines doivent être contenues dans le cercle unitaire, c’est-à-dire que leur module doit être inférieur ou égal à 1. Si une racine est située à l’extérieur du disque unité, la méthode n’est pas zéro-stable.
La seconde condition stipule qu’une racine ayant une multiplicité supérieure à 1 ne peut pas se trouver sur le bord du disque unitaire. Si une racine de multiplicité supérieure à 1 est sur le bord du disque unitaire, alors la méthode est dite semi-stable, mais pas zéro-stable.

Exemple : étudier la zéro-stabilité des méthodes Euler explicite, Euler implicite, Crank-Nicolson, de Adams à $q$ pas, de Nystrom et Milne-Simpson à $q$ pas et des méthodes BDF.

Méthodes à un pas (Euler explicite, Euler implicite, Crank-Nicolson) :

Ces méthodes ont pour polynôme caractéristique :

$ \varrho(r) = r - 1 \quad\leadsto\quad\text{il n'y a qu'une seule racine : } r = 1 $

Par conséquent, toutes ces méthodes sont zéro-stables. Ainsi, pour les méthodes à un pas, on peut conclure que :

$ \text{Convergence} \iff \text{Consistance} $
Méthodes de Adams à $q$ pas :

Ces méthodes ont pour polynôme caractéristique :

$ \varrho(r) = r^{p+1} - r^p = r^p(r - 1) \quad\leadsto\quad\text{il y a deux racines : $r = 1$ (multiplicité 1) et $r = 0$ (multiplicité $p$)} $

Ces méthodes sont donc zéro-stables. Ici aussi, on peut conclure que :

$ \text{Convergence} \iff \text{Consistance} $
Méthodes de Nystrom et Milne-Simpson à $q$ pas :

Pour ces méthodes, le polynôme caractéristique est :

$ \varrho(r) = r^{p+1} - r^{p-1} = r^{p-1}(r - 1)(r + 1) \quad\leadsto\quad\text{il y a trois racines : $r = 1$ (multiplicité 1), $r = 0$ (multiplicité $p - 1$), et $r = -1$ (multiplicité 1)} $

Ces méthodes sont également zéro-stables. Ainsi, on peut également conclure que :

$ \text{Convergence} \iff \text{Consistance} $
Méthodes BDF :

Il est possible de montrer que les méthodes BDF sont zéro-stables si et seulement si $p \leq 5$ (ce qui correspond à $q \leq 6$, comme le montre le calcul effectué avec sympy ci-dessous).

3.3 3️⃣ Ordre de convergence maximale d’une méthode multipas linéaire

Il est possible de démontrer que la zero stabilité implique une restriction sur l’ordre maximal atteignable pour une méthode multipas. On appelle cette contrainte la première barrière de Dahlquist :

⚠ Première barrière de Dahlquist [limitation de l’ordre maximal de convergence]

L’ordre $\omega$ d’une méthode multipas à $q$ étapes convergente satisfait les inégalités suivantes :

si $b_{-1}=0$ (la méthode est explicite) alors $\omega\le q$
si $b_{-1}\neq0$ (la méthode est implicite) on doit considérér deux cas
- si $q$ est impair alors $\omega\le q+1$
- si $q$ est pair alors $\omega\le q+2$

Remarque : la première barrière de Dalquist affirme qu’on peut augmenter arbitrairement l’ordre d’un schéma multipas en augmentant le nombre de pas. La convergence dépendra ensuite juste du premier polynôme caractéristique (c’est à dire de la zéro-stabilité).

Exercie : vérifier la première barrière de Dahlquist pour les méthodes Euler explicite, Euler implicite, Crank-Nicolson, de Adams-Bashforth et Adams-Moulton avec $q=1,2$ pas et Milne-Simpson avec $q=2$ pas.

Schéma	Type	Ordre maximal prévu par la barrière	Ordre réel $\omega$	Remarque
EE	Explicite	$q=1$	1	-
$\text{AB}_2$	Explicite	$q=2$	2	-
EI	Implicite, $q$ impair	$q+1 = 2$	1	Non optimal : ordre réel $1$, inférieur à l’ordre maximal $2$
CN	Implicite, $q$ impair	$q+1 = 2$	2	-
$\text{AM}_2$	Implicite, $q$ pair	$q+2 = 4$	3	Non optimal : ordre réel $3$, inférieur à l’ordre maximal $4$
$\text{MS}_2$	Implicite, $q$ pair	$q+2 = 4$	4	-

Le script suivant permet de vérifier la première barrière de Dahlquist pour une méthode donnée. Il suffit de rentrer la valeur de $p$ et le script affiche l’ordre maximal de convergence prédit par la barrière de Dahlquist ainsi que les équations à vérifier pour chaque cas.

Code

# j = 0...p # coeffs du schema
# q = p+1 # nb de pas
# ω # ordre de la méthode

p = 3
q = p+1 
ordre_max = q+2 if q%2==0 else q+1

display(Markdown(f"**On considère une méthode à q={</span>q<span class="sc">} pas (et donc p={</span>p<span class="sc">})**"))
display(Markdown(f"**Elle est d'ordre au plus {</span>ordre_max<span class="sc">}. Voici les conditions à satisfaire.**"))

aa = sp.symbols(f'a_0:{</span>q<span class="sc">}')
bb = sp.symbols(f'b_0:{</span>q<span class="sc">}')
bm1 = sp.Symbol('b_{-1}')

i = 1
sa = sum( [-j*aa[j] for j in range(len(aa))] )
sb = bm1+sum( [bb[j] for j in range(len(bb))] )
display(Markdown(f"- Pour que la méthode soit consistante (c'est-à-dire d'ordre au moins {</span>i<span class="sc">}) elle doit vérifier les deux conditions : "))
display(Markdown( r"$\qquad\qquad " + sp.latex(sp.Eq( sum(aa).factor() , 1 ) ) + "$" ))
display(Markdown( r"$\qquad\qquad " + sp.latex(sp.Eq( (sa).factor()+(i*sb).factor() , 1 ) ) + "$" ))

for i in range(2,ordre_max+1):
    sa = sum( [(-j)**i*aa[j] for j in range(len(aa))] )
    sb = bm1+sum( [(-j)**(i-1)*bb[j] for j in range(1,len(bb))] )
    display(Markdown(f"- Pour que la méthode soit d'ordre au moins {</span>i<span class="sc">} elle doit vérifier, en plus des précédentes, la condition : "))
    display(Markdown( r"$\qquad\qquad " + sp.latex(sp.Eq( (sa).factor()+(i*sb).factor() , 1 ) ) + "$" ))

On considère une méthode à q=4 pas (et donc p=3)

Elle est d’ordre au plus 6. Voici les conditions à satisfaire.

Pour que la méthode soit consistante (c’est-à-dire d’ordre au moins 1) elle doit vérifier les deux conditions :

$\qquad\qquad a_{0} + a_{1} + a_{2} + a_{3} = 1$

$\qquad\qquad - a_{1} - 2 a_{2} - 3 a_{3} + b_{0} + b_{1} + b_{2} + b_{3} + b_{-1} = 1$

Pour que la méthode soit d’ordre au moins 2 elle doit vérifier, en plus des précédentes, la condition :

$\qquad\qquad a_{1} + 4 a_{2} + 9 a_{3} - 2 \left(b_{1} + 2 b_{2} + 3 b_{3} - b_{-1}\right) = 1$

Pour que la méthode soit d’ordre au moins 3 elle doit vérifier, en plus des précédentes, la condition :

$\qquad\qquad - a_{1} - 8 a_{2} - 27 a_{3} + 3 \left(b_{1} + 4 b_{2} + 9 b_{3} + b_{-1}\right) = 1$

Pour que la méthode soit d’ordre au moins 4 elle doit vérifier, en plus des précédentes, la condition :

$\qquad\qquad a_{1} + 16 a_{2} + 81 a_{3} - 4 \left(b_{1} + 8 b_{2} + 27 b_{3} - b_{-1}\right) = 1$

Pour que la méthode soit d’ordre au moins 5 elle doit vérifier, en plus des précédentes, la condition :

$\qquad\qquad - a_{1} - 32 a_{2} - 243 a_{3} + 5 \left(b_{1} + 16 b_{2} + 81 b_{3} + b_{-1}\right) = 1$

Pour que la méthode soit d’ordre au moins 6 elle doit vérifier, en plus des précédentes, la condition :

$\qquad\qquad a_{1} + 64 a_{2} + 729 a_{3} - 6 \left(b_{1} + 32 b_{2} + 243 b_{3} - b_{-1}\right) = 1$

Récapitulatif des méthodes multipas vues jusqu’ici:

Code

sc = { <span class="st">"EE = AB_1"</span> : { <span class="st">"aa"</span>:[<span class="dv">1</span>], <span class="st">"bb"</span>:[ <span class="dv">1</span>], <span class="st">"bm1"</span>:<span class="dv">0</span>  },
       "EI = AM_0 = BDF_1" : { <span class="st">"aa"</span>:[<span class="dv">1</span>], <span class="st">"bb"</span>:[ <span class="dv">0</span>], <span class="st">"bm1"</span>:<span class="dv">1</span>  },
       "CN = AM_1" : { <span class="st">"aa"</span>:[<span class="dv">1</span>], <span class="st">"bb"</span>:[sp.Rational(<span class="dv">1</span>,<span class="dv">2</span>)], <span class="st">"bm1"</span>:<span class="dv">1</span><span class="op">/</span><span class="dv">2</span>  }, 
       "AB_2": { <span class="st">"aa"</span>:[<span class="dv">1</span>,<span class="dv">0</span>], <span class="st">"bb"</span>:[sp.Rational(<span class="dv">3</span>,<span class="dv">2</span>),sp.Rational(<span class="op">-</span><span class="dv">1</span>,<span class="dv">2</span>)], <span class="st">"bm1"</span>:<span class="dv">0</span>  }, 
       "AB_3": { <span class="st">"aa"</span>:[<span class="dv">1</span>,<span class="dv">0</span>,<span class="dv">0</span>], <span class="st">"bb"</span>:[sp.Rational(<span class="dv">23</span>,<span class="dv">12</span>),sp.Rational(<span class="op">-</span><span class="dv">16</span>,<span class="dv">12</span>), sp.Rational(<span class="dv">5</span>,<span class="dv">12</span>)], <span class="st">"bm1"</span>:<span class="dv">0</span>  }, 
       "AB_4": { <span class="st">"aa"</span>:[<span class="dv">1</span>,<span class="dv">0</span>,<span class="dv">0</span>,<span class="dv">0</span>], <span class="st">"bb"</span>:[sp.Rational(<span class="dv">55</span>,<span class="dv">24</span>),sp.Rational(<span class="op">-</span><span class="dv">59</span>,<span class="dv">24</span>), sp.Rational(<span class="dv">37</span>,<span class="dv">24</span>), sp.Rational(<span class="op">-</span><span class="dv">9</span>,<span class="dv">24</span>)], <span class="st">"bm1"</span>:<span class="dv">0</span>  }, 
       "AB_5": { <span class="st">"aa"</span>:[<span class="dv">1</span>,<span class="dv">0</span>,<span class="dv">0</span>,<span class="dv">0</span>,<span class="dv">0</span>], <span class="st">"bb"</span>:[sp.Rational(<span class="dv">1901</span>,<span class="dv">720</span>), sp.Rational(<span class="op">-</span><span class="dv">2774</span>,<span class="dv">720</span>), sp.Rational(<span class="dv">2616</span>,<span class="dv">720</span>), sp.Rational(<span class="op">-</span><span class="dv">1274</span>,<span class="dv">720</span>), sp.Rational(<span class="dv">251</span>,<span class="dv">720</span>)], <span class="st">"bm1"</span>:<span class="dv">0</span>  }, 
       "AM_2": { <span class="st">"aa"</span>:[<span class="dv">1</span>,<span class="dv">0</span>], <span class="st">"bb"</span>:[sp.Rational(<span class="dv">8</span>,<span class="dv">12</span>),sp.Rational(<span class="op">-</span><span class="dv">1</span>,<span class="dv">12</span>)], <span class="st">"bm1"</span>:sp.Rational(<span class="dv">5</span>,<span class="dv">12</span>)  }, 
       "AM_3": { <span class="st">"aa"</span>:[<span class="dv">1</span>,<span class="dv">0</span>,<span class="dv">0</span>], <span class="st">"bb"</span>:[sp.Rational(<span class="dv">19</span>,<span class="dv">24</span>),sp.Rational(<span class="op">-</span><span class="dv">5</span>,<span class="dv">24</span>),sp.Rational(<span class="dv">1</span>,<span class="dv">24</span>)], <span class="st">"bm1"</span>:sp.Rational(<span class="dv">9</span>,<span class="dv">24</span>)  }, 
       "AM_4": { <span class="st">"aa"</span>:[<span class="dv">1</span>,<span class="dv">0</span>,<span class="dv">0</span>,<span class="dv">0</span>], <span class="st">"bb"</span>:[sp.Rational(<span class="dv">646</span>,<span class="dv">720</span>),sp.Rational(<span class="op">-</span><span class="dv">264</span>,<span class="dv">720</span>),sp.Rational(<span class="dv">106</span>,<span class="dv">720</span>),sp.Rational(<span class="op">-</span><span class="dv">19</span>,<span class="dv">720</span>)], <span class="st">"bm1"</span>:sp.Rational(<span class="dv">251</span>,<span class="dv">720</span>) }, 
       "BDF_2": { <span class="st">"aa"</span>:[sp.Rational(<span class="dv">4</span>,<span class="dv">3</span>),sp.Rational(<span class="op">-</span><span class="dv">1</span>,<span class="dv">3</span>)], <span class="st">"bb"</span>:[<span class="dv">0</span>,<span class="dv">0</span>], <span class="st">"bm1"</span>:sp.Rational(<span class="dv">2</span>,<span class="dv">3</span>) }, 
       "BDF_3": { <span class="st">"aa"</span>:[sp.Rational(<span class="dv">18</span>,<span class="dv">11</span>),sp.Rational(<span class="op">-</span><span class="dv">9</span>,<span class="dv">11</span>),sp.Rational(<span class="dv">2</span>,<span class="dv">11</span>)], <span class="st">"bb"</span>:[<span class="dv">0</span>,<span class="dv">0</span>,<span class="dv">0</span>], <span class="st">"bm1"</span>:sp.Rational(<span class="dv">6</span>,<span class="dv">11</span>) }, 
       "BDF_4": { <span class="st">"aa"</span>:[sp.Rational(<span class="dv">48</span>,<span class="dv">25</span>),sp.Rational(<span class="op">-</span><span class="dv">36</span>,<span class="dv">25</span>),sp.Rational(<span class="dv">16</span>,<span class="dv">25</span>),sp.Rational(<span class="op">-</span><span class="dv">3</span>,<span class="dv">25</span>)], <span class="st">"bb"</span>:[<span class="dv">0</span>,<span class="dv">0</span>,<span class="dv">0</span>,<span class="dv">0</span>], <span class="st">"bm1"</span>:sp.Rational(<span class="dv">12</span>,<span class="dv">25</span>) }, 
       "BDF_5": { <span class="st">"aa"</span>:[sp.Rational(<span class="dv">300</span>,<span class="dv">137</span>),sp.Rational(<span class="op">-</span><span class="dv">300</span>,<span class="dv">137</span>),sp.Rational(<span class="dv">200</span>,<span class="dv">137</span>),sp.Rational(<span class="op">-</span><span class="dv">75</span>,<span class="dv">137</span>),sp.Rational(<span class="dv">12</span>,<span class="dv">137</span>)], <span class="st">"bb"</span>:[<span class="dv">0</span>,<span class="dv">0</span>,<span class="dv">0</span>,<span class="dv">0</span>,<span class="dv">0</span>], <span class="st">"bm1"</span>:sp.Rational(<span class="dv">60</span>,<span class="dv">137</span>) }, 
       "BDF_6": { <span class="st">"aa"</span>:[sp.Rational(<span class="dv">120</span>,<span class="dv">49</span>),sp.Rational(<span class="op">-</span><span class="dv">150</span>,<span class="dv">49</span>),sp.Rational(<span class="dv">400</span>,<span class="dv">147</span>),sp.Rational(<span class="op">-</span><span class="dv">75</span>,<span class="dv">49</span>),sp.Rational(<span class="dv">24</span>,<span class="dv">49</span>),sp.Rational(<span class="op">-</span><span class="dv">10</span>,<span class="dv">147</span>)], <span class="st">"bb"</span>:[<span class="dv">0</span>,<span class="dv">0</span>,<span class="dv">0</span>,<span class="dv">0</span>,<span class="dv">0</span>,<span class="dv">0</span>], <span class="st">"bm1"</span>:sp.Rational(<span class="dv">20</span>,<span class="dv">49</span>) }, 
       "MS_2": { <span class="st">"aa"</span>:[<span class="dv">0</span>,<span class="dv">1</span>], <span class="st">"bb"</span>:[sp.Rational(<span class="dv">4</span>,<span class="dv">3</span>),sp.Rational(<span class="dv">1</span>,<span class="dv">3</span>)], <span class="st">"bm1"</span>:sp.Rational(<span class="dv">1</span>,<span class="dv">3</span>) }
       } 

sp.var('r')

for schema in sc.keys():
    display(Markdown(f"**{</span>schema<span class="sc">}**"))      
    q = len(sc[schema]["aa"])
    p = q-1
    display(Markdown(f" - Schéma à {</span>q <span class="op">=</span> <span class="sc">} pas"))
    aa = sc[schema]["aa"]
    bb = sc[schema]["bb"]
    bm1 = sc[schema]["bm1"]
    
    if bm1==0:
        display(Markdown(f"- Le schéma est explicite car $b_{</span><span class="op">-</span><span class="dv">1</span><span class="sc">}=0$."))
    else:
        display(Markdown(f"- Le schéma est implicite car $b_{</span><span class="op">-</span><span class="dv">1</span><span class="sc">}={</span>bm1<span class="sc">}$."))
    
    ordre = []
    ordre.append( sum(aa)==1 and sum([-j*aa[j] for j in range(len(aa))])+bm1+sum(bb)==1  )
    # print("\tConsistance: ",end="")
    # print(ordre[-1])
    display(Markdown(f"- Consistance: {</span>ordre[<span class="op">-</span><span class="dv">1</span>]<span class="sc">}"))

    i=1
    while ordre[-1]:
        i += 1
        ordre.append( sum([(-j)**i*aa[j]+i*(-j)**(i-1)*bb[j] for j in range(len(aa))])+i*bm1==1)
    # print(f"\tOrdre {len(ordre)-1}")
    display(Markdown(f"- Ordre {</span><span class="bu">len</span>(ordre)<span class="op">-</span><span class="dv">1</span><span class="sc">}"))    
    
    rho = np.array([1])
    rho = np.append(rho,-np.array(aa))
    rho_sp = sp.Poly(rho,r).as_expr()
    # display(Math(r'\varrho(r)='+sp.latex(sp.expand(poly1d(rho)(r)))))
    display(Markdown(f"- Polynome: $\\varrho(r) = {</span>sp<span class="sc">.</span>latex(rho_sp)<span class="sc">}$"))
#     print(f"\tZéro-stabilité: |r_j|= {abs(roots(rho))}")
#     print("\tRacines: ",end="")
#     display(sp.solve(sp.expand(poly1d(rho)(r))))
    display(Markdown(f"- Ensemble des modules des racines : "))
    display( Math(r' \{|r_j|\} = '+sp.latex( [abs(rac).simplify().evalf() for rac in sp.solve(rho_sp)]  )))

EE = AB_1

Schéma à q = 1 pas

Le schéma est explicite car $b_-1=0$.

Consistance: True

Ordre 1

Polynome: $\varrho(r) = r - 1$

Ensemble des modules des racines :

$\displaystyle \{|r_j|\} = \left[ 1.0\right]$

EI = AM_0 = BDF_1

Schéma à q = 1 pas

Le schéma est implicite car $b_-1=1$.

Consistance: True

Ordre 1

Polynome: $\varrho(r) = r - 1$

Ensemble des modules des racines :

$\displaystyle \{|r_j|\} = \left[ 1.0\right]$

CN = AM_1

Schéma à q = 1 pas

Le schéma est implicite car $b_-1=0.5$.

Consistance: True

Ordre 2

Polynome: $\varrho(r) = r - 1$

Ensemble des modules des racines :

$\displaystyle \{|r_j|\} = \left[ 1.0\right]$

AB_2

Schéma à q = 2 pas

Le schéma est explicite car $b_-1=0$.

Consistance: True

Ordre 2

Polynome: $\varrho(r) = r^{2} - r$

Ensemble des modules des racines :

$\displaystyle \{|r_j|\} = \left[ 0, \ 1.0\right]$

AB_3

Schéma à q = 3 pas

Le schéma est explicite car $b_-1=0$.

Consistance: True

Ordre 3

Polynome: $\varrho(r) = r^{3} - r^{2}$

Ensemble des modules des racines :

$\displaystyle \{|r_j|\} = \left[ 0, \ 1.0\right]$

AB_4

Schéma à q = 4 pas

Le schéma est explicite car $b_-1=0$.

Consistance: True

Ordre 4

Polynome: $\varrho(r) = r^{4} - r^{3}$

Ensemble des modules des racines :

$\displaystyle \{|r_j|\} = \left[ 0, \ 1.0\right]$

AB_5

Schéma à q = 5 pas

Le schéma est explicite car $b_-1=0$.

Consistance: True

Ordre 5

Polynome: $\varrho(r) = r^{5} - r^{4}$

Ensemble des modules des racines :

$\displaystyle \{|r_j|\} = \left[ 0, \ 1.0\right]$

AM_2

Schéma à q = 2 pas

Le schéma est implicite car $b_-1=5/12$.

Consistance: True

Ordre 3

Polynome: $\varrho(r) = r^{2} - r$

Ensemble des modules des racines :

$\displaystyle \{|r_j|\} = \left[ 0, \ 1.0\right]$

AM_3

Schéma à q = 3 pas

Le schéma est implicite car $b_-1=3/8$.

Consistance: True

Ordre 4

Polynome: $\varrho(r) = r^{3} - r^{2}$

Ensemble des modules des racines :

$\displaystyle \{|r_j|\} = \left[ 0, \ 1.0\right]$

AM_4

Schéma à q = 4 pas

Le schéma est implicite car $b_-1=251/720$.

Consistance: True

Ordre 5

Polynome: $\varrho(r) = r^{4} - r^{3}$

Ensemble des modules des racines :

$\displaystyle \{|r_j|\} = \left[ 0, \ 1.0\right]$

BDF_2

Schéma à q = 2 pas

Le schéma est implicite car $b_-1=2/3$.

Consistance: True

Ordre 2

Polynome: $\varrho(r) = r^{2} - \frac{4 r}{3} + \frac{1}{3}$

Ensemble des modules des racines :

$\displaystyle \{|r_j|\} = \left[ 0.333333333333333, \ 1.0\right]$

BDF_3

Schéma à q = 3 pas

Le schéma est implicite car $b_-1=6/11$.

Consistance: True

Ordre 3

Polynome: $\varrho(r) = r^{3} - \frac{18 r^{2}}{11} + \frac{9 r}{11} - \frac{2}{11}$

Ensemble des modules des racines :

$\displaystyle \{|r_j|\} = \left[ 1.0, \ 0.426401432711221, \ 0.426401432711221\right]$

BDF_4

Schéma à q = 4 pas

Le schéma est implicite car $b_-1=12/25$.

Consistance: True

Ordre 4

Polynome: $\varrho(r) = r^{4} - \frac{48 r^{3}}{25} + \frac{36 r^{2}}{25} - \frac{16 r}{25} + \frac{3}{25}$

Ensemble des modules des racines :

$\displaystyle \{|r_j|\} = \left[ 1.0, \ 0.56086151609339, \ 0.56086151609339, \ 0.38147840911841\right]$

BDF_5

Schéma à q = 5 pas

Le schéma est implicite car $b_-1=60/137$.

Consistance: True

Ordre 5

Polynome: $\varrho(r) = r^{5} - \frac{300 r^{4}}{137} + \frac{300 r^{3}}{137} - \frac{200 r^{2}}{137} + \frac{75 r}{137} - \frac{12}{137}$

Ensemble des modules des racines :

$\displaystyle \{|r_j|\} = \left[ 1.0, \ 0.708710816266406, \ 0.417600758175733, \ 0.708710816266406, \ 0.417600758175733\right]$

BDF_6

Schéma à q = 6 pas

Le schéma est implicite car $b_-1=20/49$.

Consistance: True

Ordre 6

Polynome: $\varrho(r) = r^{6} - \frac{120 r^{5}}{49} + \frac{150 r^{4}}{49} - \frac{400 r^{3}}{147} + \frac{75 r^{2}}{49} - \frac{24 r}{49} + \frac{10}{147}$

Ensemble des modules des racines :

$\displaystyle \{|r_j|\} = \left[ 1.0, \ 0.40612326685391, \ 0.474034857706592, \ 0.474034857706592, \ 0.863380267869827, \ 0.863380267869827\right]$

MS_2

Schéma à q = 2 pas

Le schéma est implicite car $b_-1=1/3$.

Consistance: True

Ordre 4

Polynome: $\varrho(r) = r^{2} - 1$

Ensemble des modules des racines :

$\displaystyle \{|r_j|\} = \left[ 1.0, \ 1.0\right]$

4 A-stabilité (dans $\mathbb{C}$)

Dans la section précédente, nous avons abordé la résolution du problème de Cauchy sur des intervalles bornés $[t_0, T]$ . La convergence de la méthode numérique dépend de la consistance et de la zéro-stabilité. Pour étudier la consistance, on définit $h=(T-t_0)/N$ et on introduit les points équidistants $t_n = t_0 + nh$ avec $n = 0, 1, \dots, N$. On fait tendre le nombre de points $N+1$ vers l’infini (ou $h$ vers 0), tout en maintenant l’intervalle de temps $[t_0, T]$ figé. On étudie alors la limite de l’erreur de troncature locale $\tau(h)$ lorsque $h$ tend vers 0.

Cependant, dans certaines situations, il est nécessaire d’intégrer le problème de Cauchy sur des intervalles de temps très longs, voire infinis. Dans ce cas, même pour un $h$ fixé, $N$ devient infini, et des résultats tels que la zéro-stabilité ne sont plus pertinents. L’objectif ici est d’étudier la capacité des méthodes à approcher la solution sur des intervalles de temps arbitrairement grands, tout en maintenant un pas de temps $h$ fixe, et éventuellement “assez grand”. C’est ce que l’on appelle l’A-stabilité.

Définition : Schéma A-stable (dans $\mathbb{C}$)

Soit $\lambda\in\mathbb{C}$ un nombre complexe tel que $\Re(\lambda)=-\beta<0$ et considérons le problème de Cauchy

$\begin{cases} y'(t)=\lambda y(t), &\text{pour }t>0,\\ y(0)=1. \end{cases}$

Sa solution est $y(t)=e^{\lambda t}$ et comme $\Re(\lambda)<0$ alors $\lim_{t\to+\infty}|y(t)|=0.$

Soit $h>0$ un pas de temps donné, $t_n=nh$ pour $n\in\mathbb{N}$ et notons $u_n\approx y(t_n)$ une approximation de la solution $y$ au temps $t_n$.

Si, sous d’éventuelles conditions sur $h$, on a

$\lim_{n\to+\infty} |u_n| =0,$

alors on dit que le schéma est A-stable (absolument stable).

Notons $z = h\lambda$. Une méthode à $q=p+1$ pas appliquée à ce problème modèle conduit à l’équation récurrente à

$ u_{n+1} = \frac{1}{\big(1-z b_{-1}\big)}\sum_{j=0}^p \big(a_j + z b_j\big) u_{n-j} $

Définition : Région de A-stabilité (dans $\mathbb{C}$)

On appelle région de stabilité absolue $A$ d’une méthode numérique l’ensemble des nombres complexes $z = h\lambda$ pour lesquels la méthode est absolument stable : $ A=\Big\{z = h\lambda \in \mathbb{C} \ \Big| \ |u_n|\xrightarrow[n\to+\infty]{}0 \Big\} $ Une méthode numérique est inconditionellement A-stable si $\mathbb{C}^-\subset A$ où $\mathbb{C}^-=\{z\in\mathbb{C}|\Re(z)<0\}$.

🔴 Proposition [condition des racines stricte et A-stabilité] :

Une méthode multipas linéaire est absolument stable si et seulement si son polynôme de A-stabilité satisfait (éventuellement sous certaines conditions sur $h$) la condition des racines strictes. Autrement dit, les racines du polynôme

$ p_z(r) = \varrho(r) - z \sigma(r) $

doivent être strictement à l’intérieur du disque unité dans $\mathbb{C}$ :

$ \exists h_0 > 0 \quad \text{tel que} \quad |r_j(z)| < 1, \quad \forall j = 0, \dots, p, \quad \forall h \leq h_0. $

⚠ Deuxième barrière de Dahlquist : limitation sur $h$

Aucune méthode multipas explicite n’est inconditionnellement A-stable.
Aucune méthode multipas implicite d’ordre supérieur à 2 n’est inconditionnellement A-stable.

En d’autres termes, le 🎅 n’existe pas :

Seules les méthodes multipas implicites d’ordre 1 et 2 peuvent être inconditionnellement A-stables.
Méthodes multipas explicites ou Méthodes multipas implicites d’ordre supérieur à 2 $\leadsto$ toujours conditionnellement A-stables, c’est-à-dire qu’il existe une valeur maximale de $h$ pour laquelle elles restent A-stables.

🔎 Conséquences : augmenter le nombre de pas $q\dots$

améliore l’ordre de consistance
mais impose une restriction sur $h$ pour garantir l’A-stabilité
peut affecter la convergence : la zéro-stabilité devient délicate pour assurer la convergence de la méthode.

Exemples : analyse de l’A-stabilité de quelques schémas

Les schémas $\text{AB}_q$ (Adams-Bashforth) sont toujours conditionnellement A-stables car ils sont explicites.
- Par exemple, pour le schéma $\text{AB}_1$ (Euler explicite), on a :
  $ p(r) = (r - 1) - z $ La seule racine est $r = 1 + z$. Pour assurer la stabilité, il faut que $\lvert 1 + z \rvert < 1$, ce qui définit un disque ouvert de centre $(-1,0)$ et de rayon $1$ dans le plan complexe.
  Dans le cas réel, où $\varphi(t,y) = \beta y$ avec $\beta = -\Re(\lambda)$, la condition se réécrit $0 < \beta h < 1$, ce qui correspond au résultat vu en CM-4.
Les schémas $\text{AM}_q$ (Adams-Moulton) avec $q > 1$ sont conditionnellement A-stables, car ils sont implicites et d’ordre $>2$.
- Cas particulier : Euler implicite ($\text{AM}_0$)
  $ p(r) = (r - 1) - z r $ La seule racine est $r = \frac{1}{1 + z}$. La condition de stabilité est donc :
  $ \left\lvert \frac{1}{1 + z} \right\rvert < 1 $ Cette condition définit l’extérieur d’un disque de centre $(1,0)$ et de rayon $1$.
  Comme le demi-plan $\Re(z) < 0$ est inclus dans cette région, la méthode est inconditionnellement A-stable.
- Cas particulier : Crank-Nicolson ($\text{AM}_1$)
  $ p(r) = (r - 1) - z \frac{1}{2} (r + 1) $ Sa seule racine est :
  $ r = \frac{2 + z}{2 - z} $ Pour la stabilité, on impose :
  $ \left\lvert \frac{2 + z}{2 - z} \right\rvert < 1 $ Ce qui revient à exiger $\Re(z) < 0$.
  Comme $\mathbb{C}^-$ est entièrement inclus dans cette région, la méthode est inconditionnellement A-stable.

5 Exercice de synthèse : consistance, zéro-stabilité et A-stabilité des schémas EE, EI, CN

Pour les méthodes d’Euler explicite, Euler implicite et Cranck-Nicolson :

Trouver les coefficients $p\ge0$, $\{a_j\}_{j=0}^p$ et $\{b_j\}_{j=-1}^p$ tels que $ u_{n+1} = \sum_{j=0}^p a_ju_{n-j}+h\sum_{j=0}^p b_j\varphi(t_{n-j},u_{n-j})+hb_{-1}\varphi(t_{n+1},u_{n+1}), \qquad n=p,p+1,\dots,N-1$
Calculer les $p+1$ racines $\{r_j\}_{j=0}^p$ du premier polynôme caractéristique $\varrho(r)=r^{p+1}-\sum_{j=0}^p a_jr^{p-j}.$ En déduire que la méthode est zéro-stable, i.e. que $ \begin{cases} |r_j| \le 1 \quad\text{pour tout } j=0,\dots,p \\ r_j \text{ a multiplicité} >1 \quad\implies \quad |r_j|<1.\end{cases} $
Donner l’ordre de consistance maximal théorique puis étudier l’ordre de consistance réel, autrement dit trouver le plus grand $\omega\ge1$ tel que $\xi(0)=\xi(1)=\dots=\xi(\omega)=1$.
Conclure sur la convergence de la méthode et son ordre de convergence.
Étudier la A-stabilité

Il s’agit de trois méthodes à $q=1$ pas, donc $p=0$.

Commençons par l’étude de la convergence en étudiant la consistance (et son ordre) et la zéro-stabilité.

Selon la première barrière de Dahlquist, si la méthode est explicite l’ordre de convergence maximal est 2 (car $q$ impair), si la méthode est explicite l’ordre maximal est 1. Pour pouvoir étudier l’ordre de consistance, commençons par afficher les $\xi(i)$ pour $i=0,1,2$ :

Code

xi_cond(p=0, omega=2)

Pour $p=0$, on a une méthode à $q=1$ pas et on affiche $ξ(i)$ pour $i=0,...,2$

$\xi(0) = a_{0}$

$\xi(1) = b_{0} + b_{-1}$

$\xi(2) = 2 b_{-1}$

Résumons donc les quantités indiquées dans le tableau suivant :

\( \begin{array}{|c|c|c|c|} \hline & \textbf{EE} & \textbf{EI} & \textbf{CN} \\ \hline \textbf{Méthode : } u_{n+1} = & u_n + h \varphi_n & u_n + h \varphi_{n+1} & u_n + \frac{h}{2} \big(\varphi_{n+1} + \varphi_n\big) \\ \hline \textbf{Coefficients : } p = 0 \text{ et } & a_0 = 1, b_{-1} = 0, b_0 = 1 & a_0 = 1, b_{-1} = 1, b_0 = 0 & a_0 = 1, b_{-1} = \frac{1}{2}, b_0 = \frac{1}{2} \\ \hline \textbf{Polynôme caractéristique : } \varrho & \varrho(r) = r - 1 & \varrho(r) = r - 1 & \varrho(r) = r - 1 \\ \hline \textbf{Racines : } & r_0 = 1 & r_0 = 1 & r_0 = 1 \\ \hline \textbf{Zéro-stabilité : } & \text{oui, } \lvert r_0 \rvert = 1 \text{ et mult. 1} & \text{oui, } \lvert r_0 \rvert = 1 \text{ et mult. 1} & \text{oui, } \lvert r_0 \rvert = 1 \text{ et mult. 1} \\ \hline \textbf{Consistance : } & \text{oui, } \xi(0) = 1, \xi(1) = 1 & \text{oui, } \xi(0) = 1, \xi(1) = 1 & \text{oui, } \xi(0) = 1, \xi(1) = 1 \\ \hline \textbf{Ordre maximal (Dahlquist) : } & \omega \le 1 & \omega \le 2 & \omega \le 2 \\ \hline \textbf{Ordre réel : } \omega & \omega = 1 & \omega = 1 \text{ car } \xi(2) = 2 \neq 1 & \omega = 2 \text{ car } \xi(2) = 1 \\ \hline \end{array} \)

Passons maintenant à l’étude de la A-stabilité. Pour cela, considérons le toy-model : soit $\lambda\in\mathbb{C}$ un nombre complexe tel que $\Re(\lambda)=-\beta<0$ et considérons le problème de Cauchy

$\begin{cases} y'(t)=\lambda y(t), &\text{pour }t>0,\\ y(0)=1. \end{cases}$

Posons $z = \lambda h$ et calculons les racines du polynôme caractéristique $p_z(r) = \varrho(r) - z \sigma(r)$ :

$ \begin{array}{|c|c|c|c|} \hline & \textbf{EE} & \textbf{EI} & \textbf{CN} \\ \hline \textbf{Schéma appliqué au toy-model} & u_n = (1 + z)^n & u_n = \left(\frac{1}{1 + z}\right)^n & u_n = \left(\frac{2 + z}{2 - z}\right)^n \\ \hline \textbf{Condition pour } \lvert u_n \rvert \xrightarrow[n\to\infty]{}0 & \lvert 1 + z \rvert < 1 & \left\lvert \frac{1}{1 + z} \right\rvert < 1 & \left\lvert \frac{2 + z}{2 - z} \right\rvert < 1 \\ \hline \textbf{A-stabilité ?} & \textbf{Uniquement} \text{ si } -2 < |z| < 0 & \textbf{Oui} \text{ (car } \Re(\lambda) < 0\text{)} & \textbf{Oui} \text{ (car } \Re(\lambda) < 0\text{)} \\ \hline \end{array} $

Conclusion :

Euler explicite : la méthode est consistante d’ordre $\omega = 1$ qui est l’ordre maximal prévu par la barrière de Dahlquist (schéma explicite). Le schéma étant aussi zéro-stable, il est donc convergent d’ordre 1. Concerant la A-stabilité, il est nécessaire que $-2 < |z| < 0$ pour que la méthode soit A-stable. Dans $\mathbb{R}$, cela implique $0 < \beta h < 2$.
Euler implicite : la méthode est consistante d’ordre $\omega = 1$ qui est inférieur à l’ordre maximal prévu par la barrière de Dahlquist (schéma implicite). Le schéma étant aussi zéro-stable, il est donc convergent d’ordre 1. Concernant la A-stabilité, la méthode est inconditionellement A-stable.
Cranck-Nicolson : la méthode est consistante d’ordre $\omega = 1$ qui est inférieur à l’ordre maximal prévu par la barrière de Dahlquist (schéma implicite). Le schéma étant aussi zéro-stable, il est donc convergent d’ordre 1. Concernant la A-stabilité, la méthode est inconditionellement A-stable.

6 Propriétés des schémas Prédicteur-Correcteur basés sur les méthodes multi-pas

Ordre : si on note

$\omega_{[P]}$ l’ordre du predictor (schéma explicite)
$\omega_{[C]}$ l’ordre du corrector (schéma implicite)

alors l’ordre du schéma predictor-corrector est donné par

$ \omega_{[PC]}=\min\Big\{\omega_{[C]},\omega_{[P]}+1\Big\} $

Ainsi, pour obtenir une méthode d’ordre $\omega$, on peut choisir un prédicteur d’ordre $\omega-1$ et un correcteur d’ordre $\omega$ (par exemple, deux méthodes d’Adam ayant le même nombre de pas).

Zéro-stabilité : on peut démontrer que la zéro-stabilité du prédicteur n’influe pas sur la zéro-stabilité de la méthode prédicteur-correcteur. Il est même possible d’utiliser un prédicteur instable.

A-stabilité : les méthodes predictor-corrector sont soumises à une condition de A-stabilité, qui est typiquement celle du prédicteur. Elles ne sont donc pas adaptées à la résolution de problèmes de Cauchy sur des intervalles non bornés ou de problèmes stiff.

7 Méthodes cycliques composites : comment surmonter les limites de Dahlquist

On peut surmonter les limites imposées par les barrières de Dahlquist en combinant plusieurs méthodes multi-pas. Par exemple, les deux méthodes suivantes à trois pas

$ \begin{align*} u_{n+1} &= -\frac{8}{11}u_{n} + \frac{19}{11}u_{n-1} + \frac{h}{30} \big( 30\varphi_{n+1}+57\varphi_n+24\varphi_{n-1}-\varphi_{n-2} \big) \\ u_{n+1} &= \frac{449}{240}u_{n} - \frac{19}{30}u_{n-1} -\frac{361}{240}u_{n-2} + \frac{h}{720}\big(251\varphi_{n+1}+456\varphi_n-1347\varphi_{n-1}-350\varphi_{n-2}\big) \end{align*} $

sont d’ordre cinq, mais sont instables. Cependant, en les combinant comme suit

$ u_{n+1} = \begin{cases} -\frac{8}{11}u_{n} + \frac{19}{11}u_{n-1} + \frac{h}{30} \big( 30\varphi_{n+1}+57\varphi_n+24\varphi_{n-1}-\varphi_{n-2} \big) &\text{si $n$ est pair}\\ \frac{449}{240}u_{n} - \frac{19}{30}u_{n-1} -\frac{361}{240}u_{n-2} + \frac{h}{720}\big(251\varphi_{n+1}+456\varphi_n-1347\varphi_{n-1}-350\varphi_{n-2}\big) &\text{sinon.} \end{cases} $

on obtient une méthode A-stable à trois pas d’ordre cinq.

8 Affichage des régions de A-stabilité

Les images affichées ci-dessous montrent les régions de A-stabilité des quelques méthodes vues en précédence et sont issues du livre
A. Quarteroni, F. Saleri, P. Gervasio Calcul Scientifique: Cours, exercices corrigés et illustrations en Matlab et Octave.

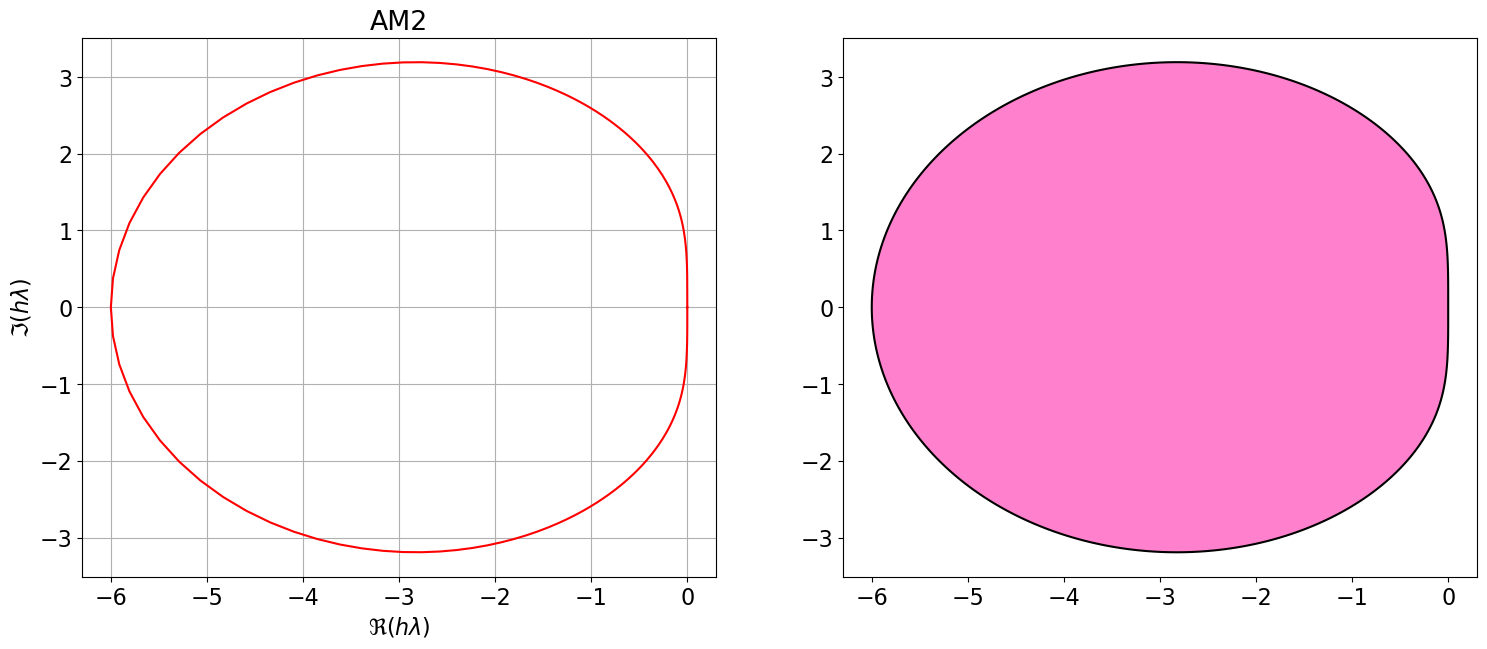
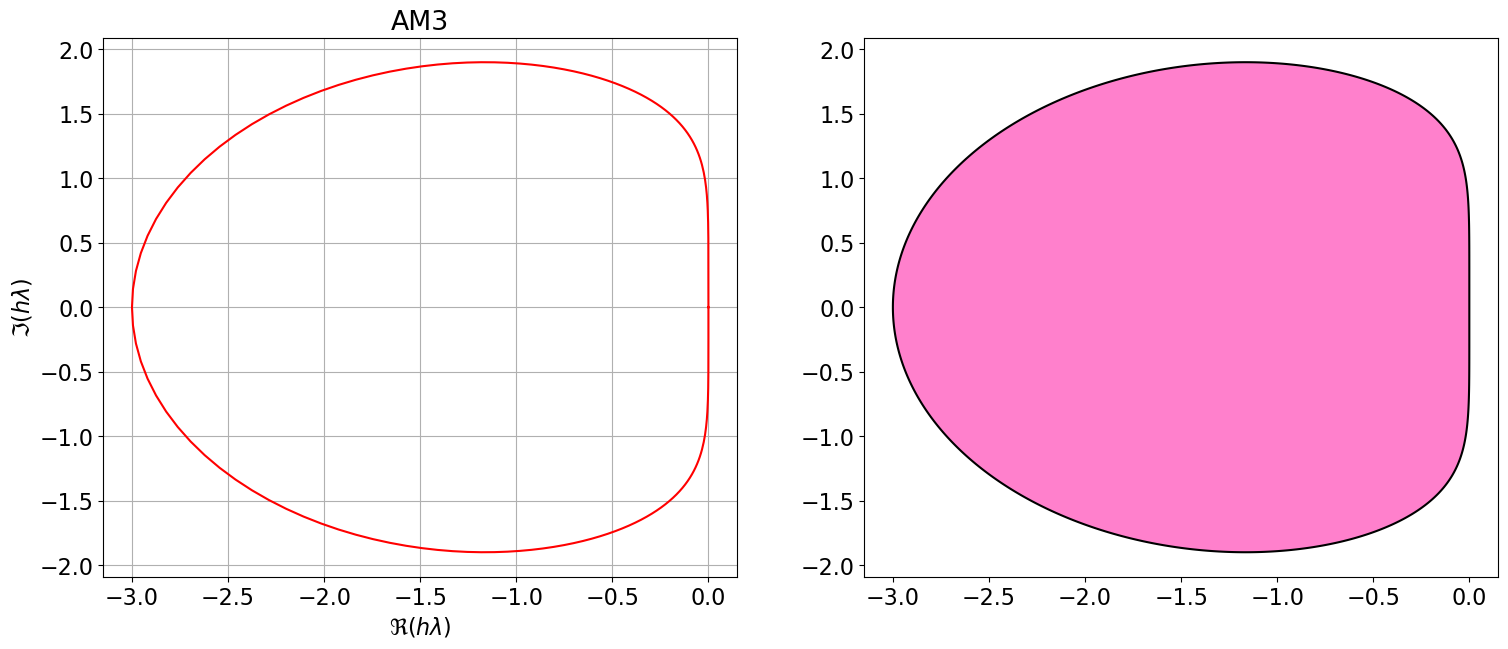
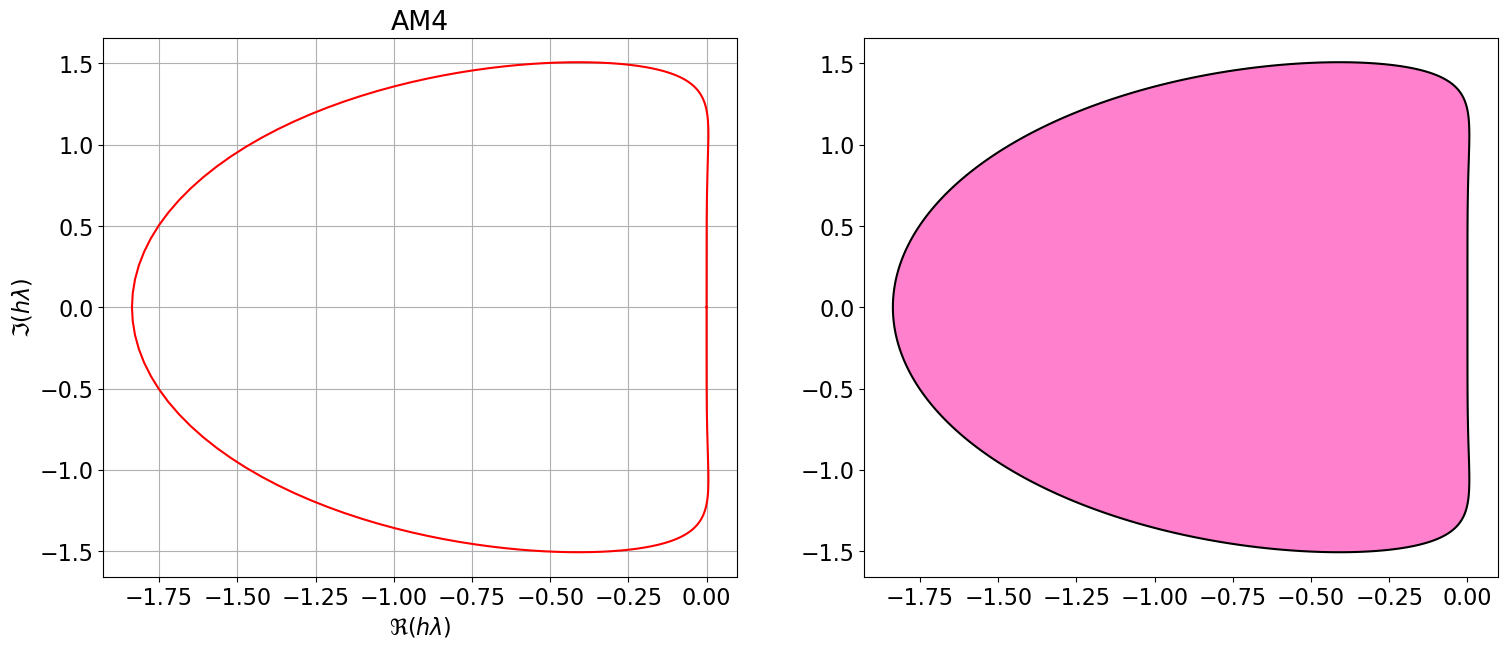
8.1 Régions de A-stabilité des méthodes d’Adams-Bashforth et d’Adams-Moulton

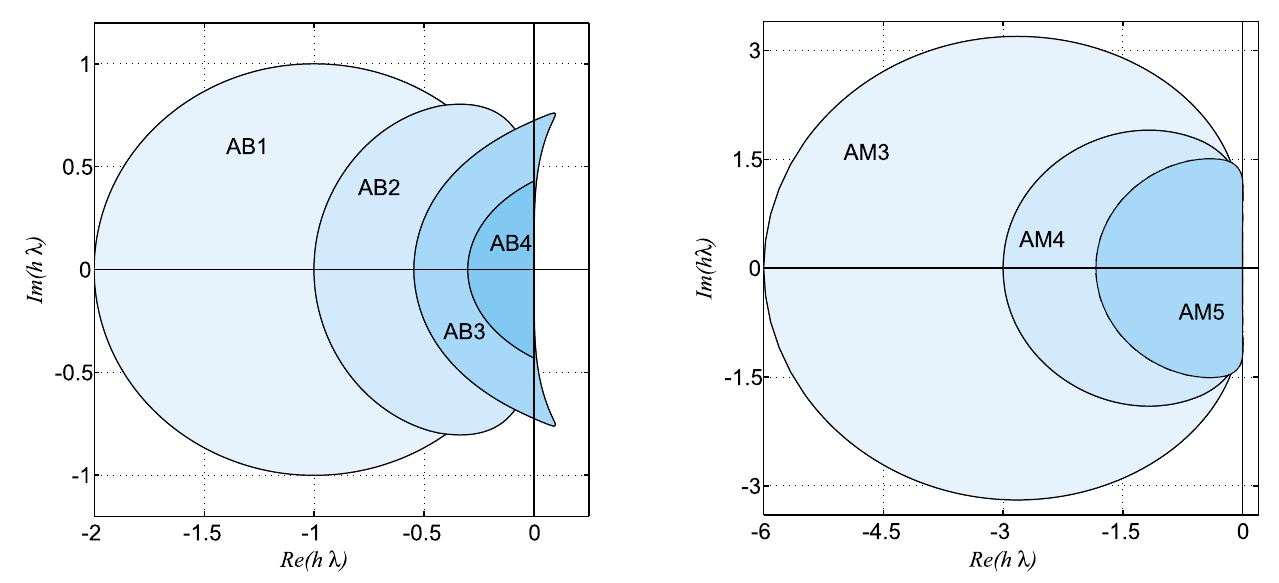
Les figures ci-dessous illustrent les régions de stabilité absolue des méthodes :
- À gauche : Adams-Bashforth (AB), qui sont des schémas explicites.
- À droite : Adams-Moulton (AM), qui sont des schémas implicites.

On observe que :
- Ces régions sont bornées et diminuent à mesure que l’ordre augmente.
- De plus, toutes les méthodes explicites et les méthodes implicites d’ordre supérieur à 2 ne sont pas inconditionnellement A-stables.
- Elles ne conviennent donc pas aux problèmes nécessitant une intégration sur de très longs intervalles de temps, car elles imposent une contrainte sur la taille du pas de temps $h$.

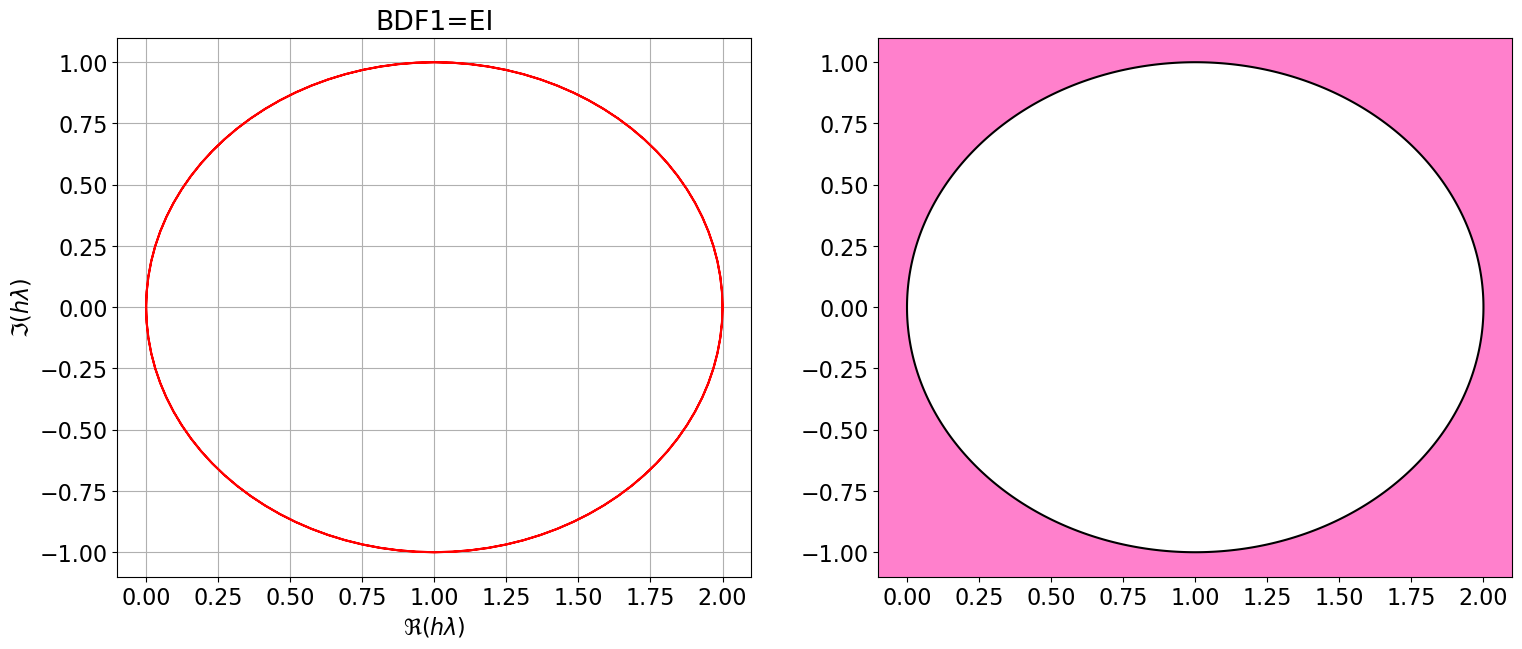
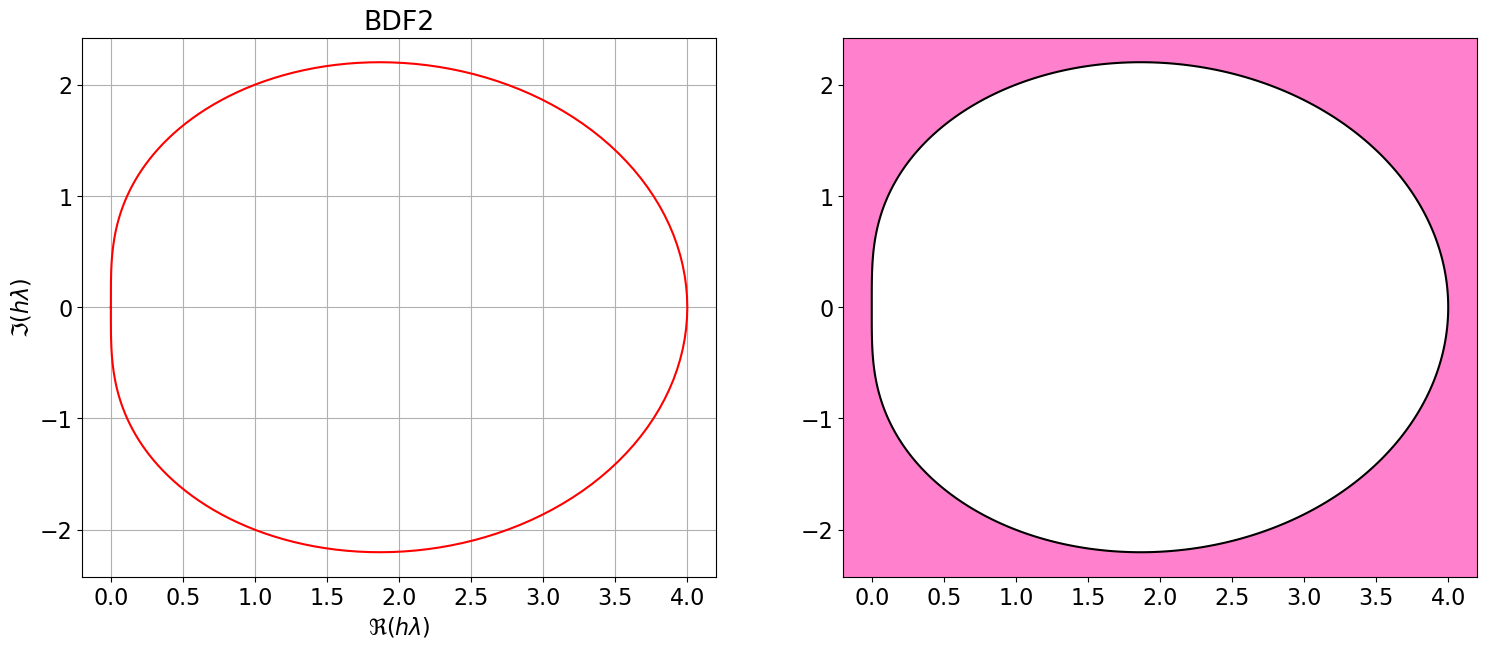
8.2 Régions de A-stabilité des méthodes BDF

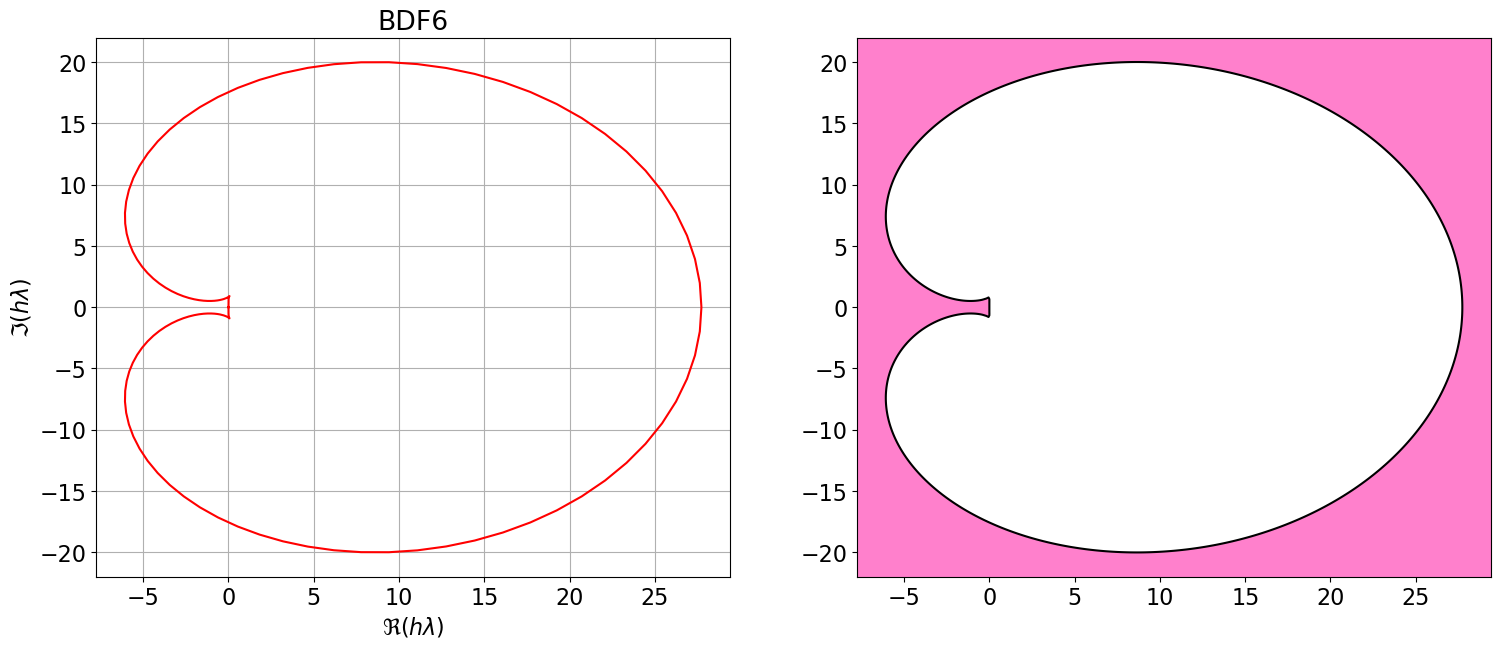
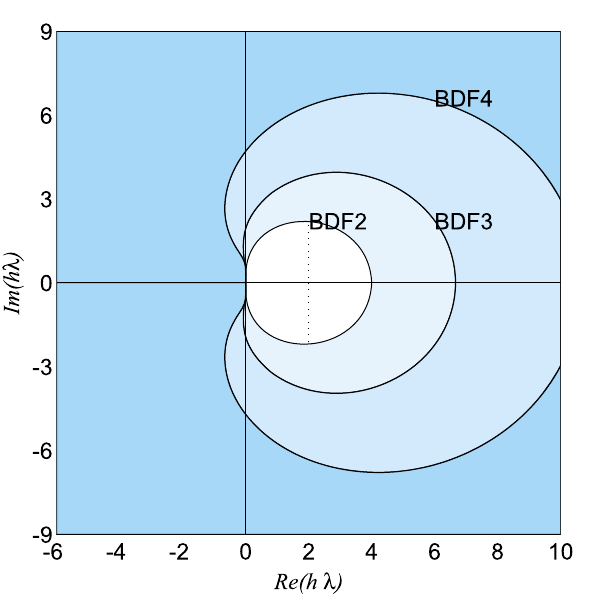
L’illustration ci-dessous montre les régions de stabilité absolue des méthodes Backward Differentiation Formula (BDF) pour $q \leq 4$ qui sont des schémas implicites.

Contrairement aux méthodes d’Adams :
- Les régions de stabilité des BDF sont conditionnellement A-stable sur $\mathbb{C}$ mais incluent toujours l’axe réel négatif, ce qui leur confère une inconditionnelle A-stabilité sur $\mathbb{R}$.
- Ces méthodes sont donc particulièrement adaptées aux problèmes nécessitant une intégration sur des intervalles de temps très longs, voire infinis.
- Elles sont aussi privilégiées pour la résolution des problèmes raides, car, avec un changement de variable, cela revient à résoudre un problème de Cauchy sur un intervalle de temps grand.

8.3 Annexe : comment tracer les régions de A-stabilité ?

Posons $z=h\lambda$. Il est en général difficile de déterminer la région de stabilité absolue car on doit décider pour quels $z\in\mathbb{C}$ les racines du polynôme de stabilité vérifient la condition de racines stricte (i.e. $|r| < 1$). Il est plus aisé de déterminer la frontière de cette région car au moins une des racines de $p$ à la frontière est de module $1$. On a donc $|r| = 1$ sur $\partial A$. La frontière de $A$ est alors un sous ensemble des points $z\in\mathbb{C}$ pour lesquels $r=e^{i\vartheta}$, $\vartheta\in\mathbb{R}$. On remplace alors $r =e^{i\vartheta}$ dans $p$ et comme $e^{i\vartheta}$ est racine, $p(e^{i\vartheta}) = 0$ et on résoud l’équation. On obtient $z = z(\vartheta)$ ce qui donne une courbe dans $\mathbb{C}$ en fonction de l’angle $\vartheta$, ce qui décrit donc une courbe polaire. Par conséquent, pour obtenir une représentation approchée de $\partial A$, il suffit d’évaluer le second membre pour diverses valeurs de $r$ sur le cercle unité, diverses valeurs de $\vartheta\in\mathbb{R}$ et $r=e^{i\vartheta}$.

Code

def polyCar(schema):
    sp.var('r z')
    p,aa,bb,bm1=schema["p"],schema["aa"],schema["bb"],schema["bm1"]   
    rho = r**(p+1)-sum(aa[j]*r**(p-j)for j in range(p+1))    
    sigma = bm1*r**(p+1)+sum(bb[j]*r**(p-j)for j in range(p+1))
    display(Math(r'\varrho(r)='+sp.latex(rho)))
    display(Math(r'\sigma(r)='+sp.latex(sigma)))
    

def polyCarIMPL(schema):
    sp.var('r z')
    p,aa,bb,bm1=schema["p"],schema["aa"],schema["bb"],schema["bm1"]  
    rho=r**(p+1)-sum(aa[j]*r**(p-j)for j in range(p))    
    sigma=bm1*r**(p+1)+sum(bb[j]*r**(p-j)for j in range(p))
    display(Math(r'\varrho(r)='+sp.latex(rho)))
    display(Math(r'\sigma(r)='+sp.latex(sigma)))
    
    

# Returns > 1 if argument is not in region of absolute stability
def stabilityFunction(z,schema):
    schema["aa"] = [float(a) for a in schema["aa"]]
    schema["bb"] = [float(b) for b in schema["bb"]]
    schema["bm1"] = float(schema["bm1"])
    pol = np.array(schema["aa"])+z*np.array(schema["bb"])
    pol = np.append([1-z*schema["bm1"]],-pol)
    return max(abs(np.roots(pol)))


def Astabilite(schema):
    schema["aa"] = [float(a) for a in schema["aa"]]
    schema["bb"] = [float(b) for b in schema["bb"]]
    schema["bm1"] = float(schema["bm1"])
    p,aa,bb,bm1=schema["p"],schema["aa"],schema["bb"],schema["bm1"]
    
    # cc liste de points sur le circle unitaire
    rr = np.linspace(0,2*np.pi,201)
    cc = np.cos(rr)+1j*np.sin(rr) 
    ## ff fonction vectorisée qui donne zz
    ff = lambda cc,p,aa,bb,bm1 : (cc**(p+1)-np.polyval(aa,cc))/(bm1*cc**(p+1)+np.polyval(bb,cc)) 
    zz = ff(cc,p,aa,bb,bm1)
    
    plt.figure(figsize=(18,7))
    plt.subplot(1,2,1)
    plt.plot(zz.real,zz.imag,'r')
    plt.grid(True)
#     plt.axis('equal')
    plt.xlabel(r'$\Re(h\lambda)$')
    plt.ylabel(r'$\Im(h\lambda)$');
    plt.title(schema["Nom"])
    Lx,Ly = plt.xlim(),plt.ylim()
    
    plt.subplot(1,2,2)
    x = np.linspace(Lx[0],Lx[1], 300)
    y = np.linspace(Ly[0],Ly[1], 300)
    [X,Y] = np.meshgrid(x,y)
    Z = np.zeros(X.shape)
    for m in range(X.shape[0]):
        for n in range(X.shape[1]):
            Z[m,n] = stabilityFunction(X[m,n] + 1j * Y[m,n], schema)
    plt.contour(X, Y, Z, [1], colors='k')
    plt.contourf(X, Y, Z, [0,1], colors=[[1, 0.5, 0.8]])
    return None

Code

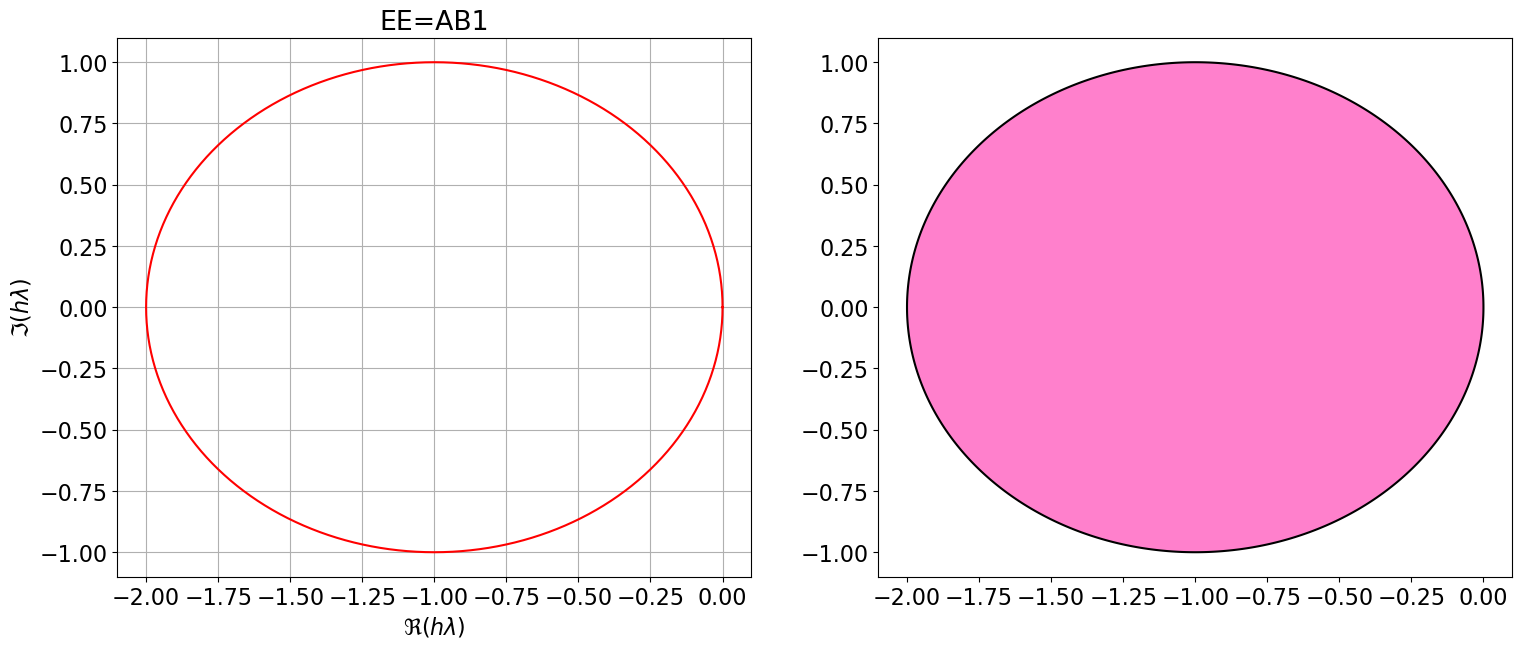
EE = { <span class="st">"Nom"</span>:<span class="st">"EE=AB1"</span>, <span class="st">"p"</span>:<span class="dv">0</span>, <span class="st">"aa"</span>:[<span class="dv">1</span>], <span class="st">"bb"</span>:[<span class="dv">1</span>], <span class="st">"bm1"</span>:<span class="dv">0</span>  }
polyCar(EE)
Astabilite(EE)

$\displaystyle \varrho(r)=r - 1$

$\displaystyle \sigma(r)=1$

Code

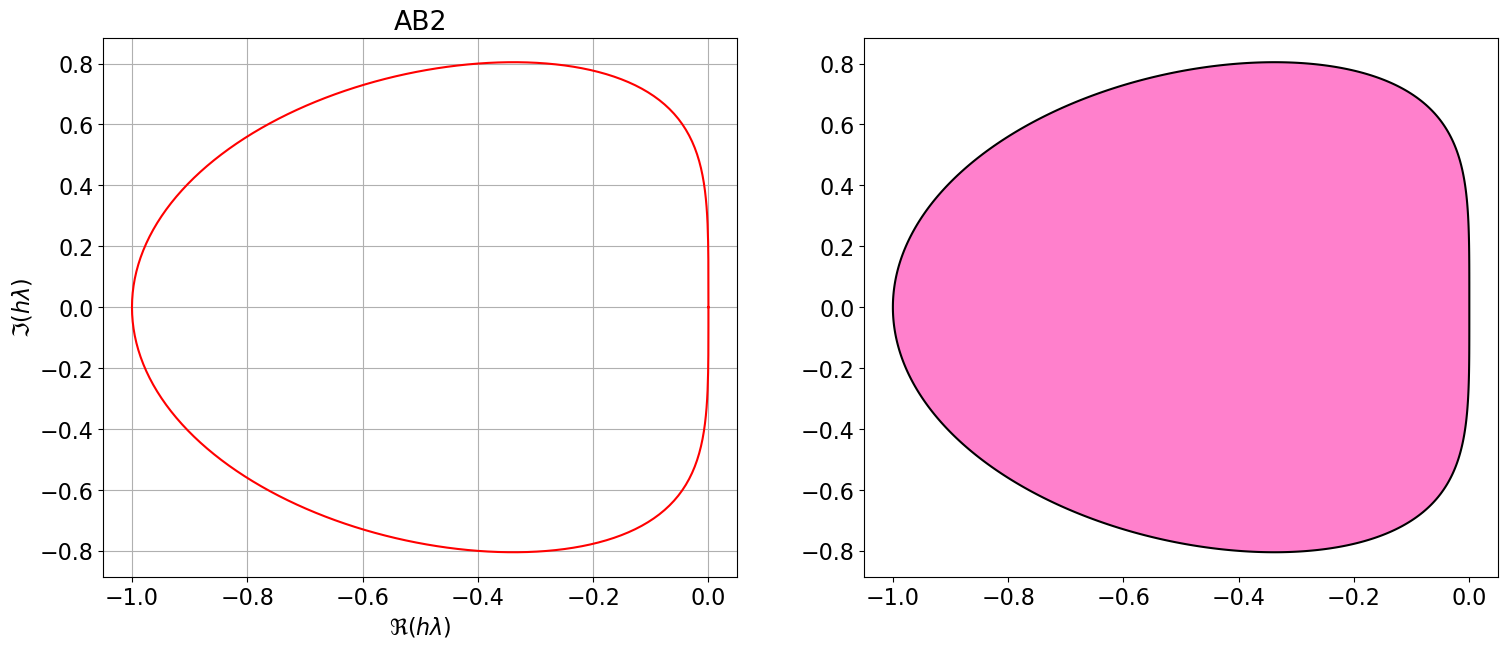
AB2 = { <span class="st">"Nom"</span>:<span class="st">"AB2"</span>, <span class="st">"p"</span>:<span class="dv">1</span>, <span class="st">"aa"</span>:[<span class="dv">1</span>,<span class="dv">0</span>], <span class="st">"bb"</span>:[sp.Rational(<span class="dv">3</span>,<span class="dv">2</span>),<span class="op">-</span>sp.Rational(<span class="dv">1</span>,<span class="dv">2</span>)], <span class="st">"bm1"</span>:<span class="dv">0</span>  }
polyCar(AB2)
Astabilite(AB2)

$\displaystyle \varrho(r)=r^{2} - r$

$\displaystyle \sigma(r)=\frac{3 r}{2} - \frac{1}{2}$

Code

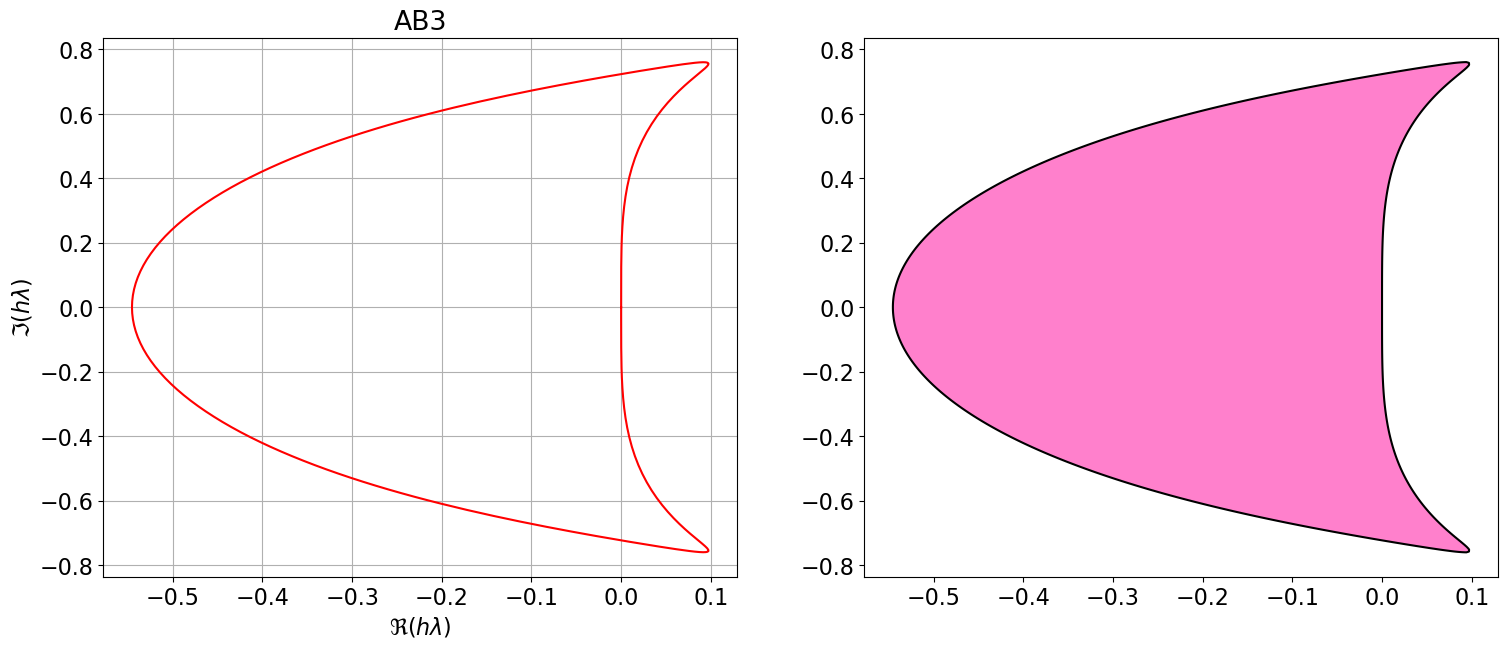
AB3 = { <span class="st">"Nom"</span>:<span class="st">"AB3"</span>, <span class="st">"p"</span>:<span class="dv">2</span>, <span class="st">"aa"</span>:[<span class="dv">1</span>,<span class="dv">0</span>,<span class="dv">0</span>], <span class="st">"bb"</span>:[sp.Rational(<span class="dv">23</span>,<span class="dv">12</span>),<span class="op">-</span>sp.Rational(<span class="dv">16</span>,<span class="dv">12</span>), sp.Rational(<span class="dv">5</span>,<span class="dv">12</span>)], <span class="st">"bm1"</span>:<span class="dv">0</span>  }
polyCar(AB3)
Astabilite(AB3)

$\displaystyle \varrho(r)=r^{3} - r^{2}$

$\displaystyle \sigma(r)=\frac{23 r^{2}}{12} - \frac{4 r}{3} + \frac{5}{12}$

Code

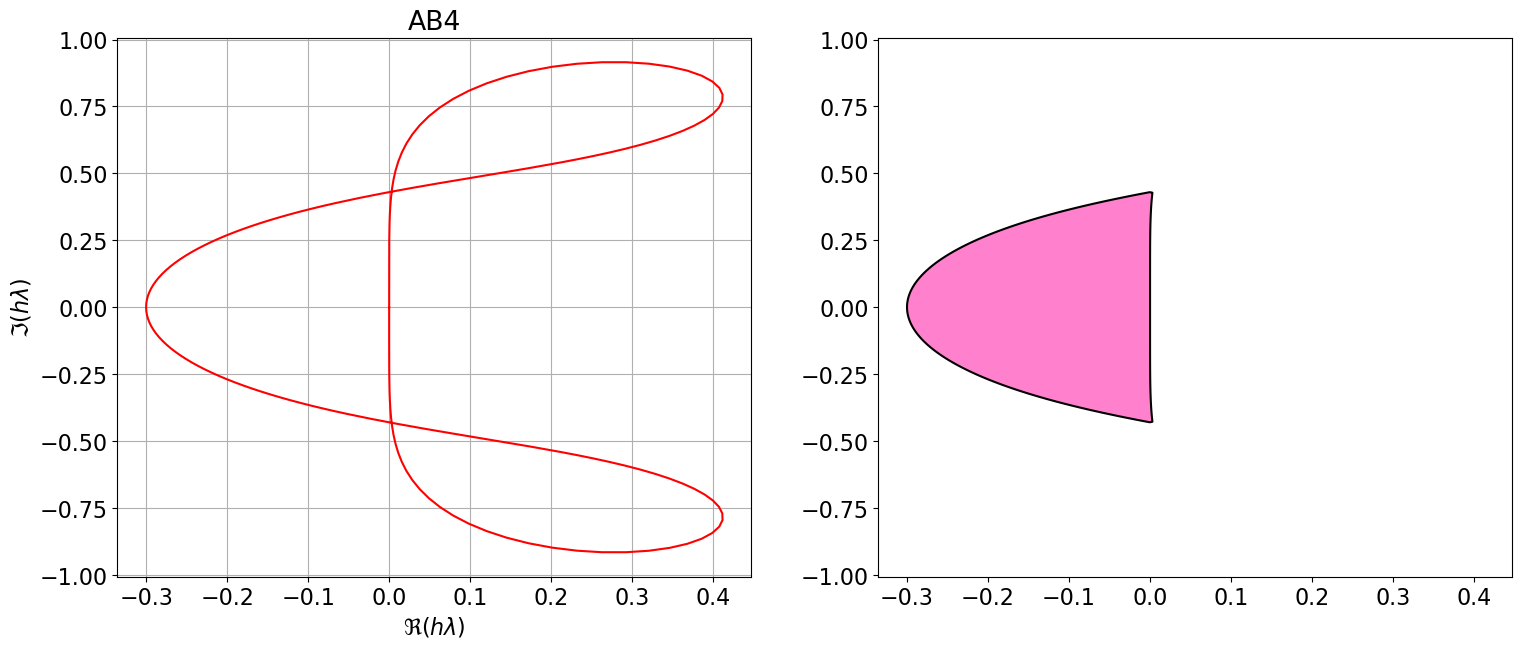
AB4 = { <span class="st">"Nom"</span>:<span class="st">"AB4"</span>, <span class="st">"p"</span>:<span class="dv">3</span>, <span class="st">"aa"</span>:[<span class="dv">1</span>,<span class="dv">0</span>,<span class="dv">0</span>,<span class="dv">0</span>], <span class="st">"bb"</span>:[sp.Rational(<span class="dv">55</span>,<span class="dv">24</span>),<span class="op">-</span>sp.Rational(<span class="dv">59</span>,<span class="dv">24</span>), sp.Rational(<span class="dv">37</span>,<span class="dv">24</span>), <span class="op">-</span>sp.Rational(<span class="dv">9</span>,<span class="dv">24</span>)], <span class="st">"bm1"</span>:<span class="dv">0</span>  }
polyCar(AB4)
Astabilite(AB4)

$\displaystyle \varrho(r)=r^{4} - r^{3}$

$\displaystyle \sigma(r)=\frac{55 r^{3}}{24} - \frac{59 r^{2}}{24} + \frac{37 r}{24} - \frac{3}{8}$

Code

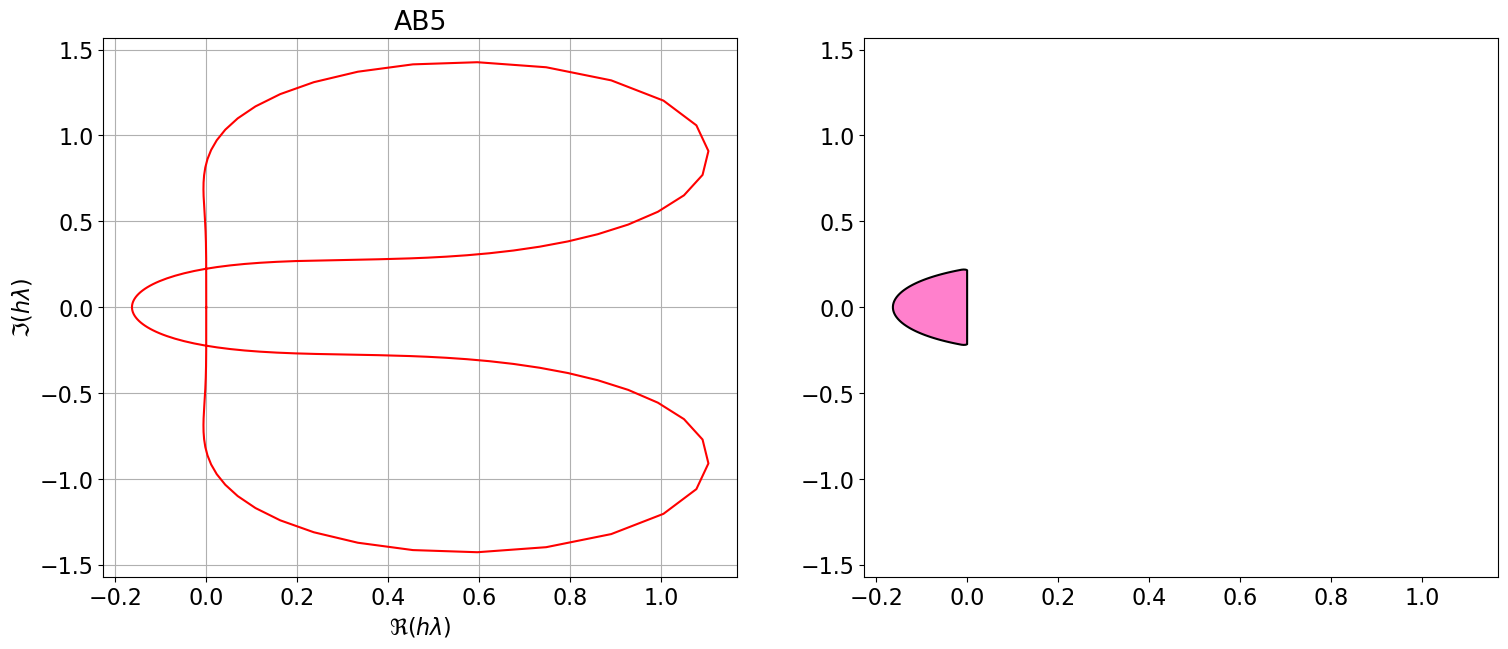
AB5 = { <span class="st">"Nom"</span>:<span class="st">"AB5"</span>, <span class="st">"p"</span>:<span class="dv">4</span>, <span class="st">"aa"</span>:[<span class="dv">1</span>,<span class="dv">0</span>,<span class="dv">0</span>,<span class="dv">0</span>,<span class="dv">0</span>], <span class="st">"bb"</span>:[sp.Rational(<span class="dv">1901</span>,<span class="dv">720</span>), <span class="op">-</span>sp.Rational(<span class="dv">1387</span>,<span class="dv">360</span>), sp.Rational(<span class="dv">109</span>,<span class="dv">30</span>), <span class="op">-</span>sp.Rational(<span class="dv">637</span>,<span class="dv">360</span>), sp.Rational(<span class="dv">251</span>,<span class="dv">720</span>)], <span class="st">"bm1"</span>:<span class="dv">0</span>  }
polyCar(AB5)
Astabilite(AB5)

$\displaystyle \varrho(r)=r^{5} - r^{4}$

$\displaystyle \sigma(r)=\frac{1901 r^{4}}{720} - \frac{1387 r^{3}}{360} + \frac{109 r^{2}}{30} - \frac{637 r}{360} + \frac{251}{720}$

Code

AM0 = { <span class="st">"Nom"</span>:<span class="st">"AM0=EI"</span>, <span class="st">"p"</span>:<span class="dv">0</span>, <span class="st">"aa"</span>:[<span class="dv">1</span>], <span class="st">"bb"</span>:[<span class="dv">0</span>], <span class="st">"bm1"</span>: <span class="dv">1</span>  }
polyCarIMPL(AM0)
#Astabilite(AM0)

$\displaystyle \varrho(r)=r$

$\displaystyle \sigma(r)=r$

Code

AM1 = { <span class="st">"Nom"</span>:<span class="st">"AM1=CN"</span>, <span class="st">"p"</span>:<span class="dv">1</span>, <span class="st">"aa"</span>:[<span class="dv">1</span>], <span class="st">"bb"</span>:[sp.Rational(<span class="dv">1</span>,<span class="dv">2</span>)], <span class="st">"bm1"</span>: sp.Rational(<span class="dv">1</span>,<span class="dv">2</span>)  }
polyCarIMPL(AM1)
#Astabilite(AM1)

$\displaystyle \varrho(r)=r^{2} - r$

$\displaystyle \sigma(r)=\frac{r^{2}}{2} + \frac{r}{2}$

Code

AM2 = { <span class="st">"Nom"</span>:<span class="st">"AM2"</span>, <span class="st">"p"</span>:<span class="dv">1</span>, <span class="st">"aa"</span>:[<span class="dv">1</span>,<span class="dv">0</span>], <span class="st">"bb"</span>:[sp.Rational(<span class="dv">8</span>,<span class="dv">12</span>),<span class="op">-</span>sp.Rational(<span class="dv">1</span>,<span class="dv">12</span>)], <span class="st">"bm1"</span>:sp.Rational(<span class="dv">5</span>,<span class="dv">12</span>) }
polyCar(AM2)
Astabilite(AM2)

$\displaystyle \varrho(r)=r^{2} - r$

$\displaystyle \sigma(r)=\frac{5 r^{2}}{12} + \frac{2 r}{3} - \frac{1}{12}$

Code

AM3 = { <span class="st">"Nom"</span>:<span class="st">"AM3"</span>, <span class="st">"p"</span>:<span class="dv">2</span>, <span class="st">"aa"</span>:[<span class="dv">1</span>,<span class="dv">0</span>,<span class="dv">0</span>], <span class="st">"bb"</span>:[sp.Rational(<span class="dv">19</span>,<span class="dv">24</span>),<span class="op">-</span>sp.Rational(<span class="dv">5</span>,<span class="dv">24</span>),sp.Rational(<span class="dv">1</span>,<span class="dv">24</span>)], <span class="st">"bm1"</span>:sp.Rational(<span class="dv">9</span>,<span class="dv">24</span>)  }
polyCar(AM3)
Astabilite(AM3)

$\displaystyle \varrho(r)=r^{3} - r^{2}$

$\displaystyle \sigma(r)=\frac{3 r^{3}}{8} + \frac{19 r^{2}}{24} - \frac{5 r}{24} + \frac{1}{24}$

Code

AM4 = { <span class="st">"Nom"</span>:<span class="st">"AM4"</span>, <span class="st">"p"</span>:<span class="dv">3</span>, <span class="st">"aa"</span>:[<span class="dv">1</span>,<span class="dv">0</span>,<span class="dv">0</span>,<span class="dv">0</span>], <span class="st">"bb"</span>:[sp.Rational(<span class="dv">646</span>,<span class="dv">720</span>), sp.Rational(<span class="op">-</span><span class="dv">264</span>,<span class="dv">720</span>), sp.Rational(<span class="dv">106</span>,<span class="dv">720</span>), sp.Rational(<span class="op">-</span><span class="dv">19</span>,<span class="dv">720</span>)], <span class="st">"bm1"</span>:sp.Rational(<span class="dv">251</span>,<span class="dv">720</span>)  }
polyCar(AM4)
Astabilite(AM4)

$\displaystyle \varrho(r)=r^{4} - r^{3}$

$\displaystyle \sigma(r)=\frac{251 r^{4}}{720} + \frac{323 r^{3}}{360} - \frac{11 r^{2}}{30} + \frac{53 r}{360} - \frac{19}{720}$

Code

MS2 = { <span class="st">"Nom"</span>:<span class="st">"MS2"</span>, <span class="st">"p"</span>:<span class="dv">1</span>, <span class="st">"aa"</span>:[<span class="dv">0</span>,<span class="dv">1</span>], <span class="st">"bb"</span>:[sp.Rational(<span class="dv">4</span>,<span class="dv">3</span>),sp.Rational(<span class="dv">1</span>,<span class="dv">3</span>)], <span class="st">"bm1"</span>:sp.Rational(<span class="dv">1</span>,<span class="dv">3</span>) }
polyCar(MS2)
#Astabilite(MS2)

$\displaystyle \varrho(r)=r^{2} - 1$

$\displaystyle \sigma(r)=\frac{r^{2}}{3} + \frac{4 r}{3} + \frac{1}{3}$

Code

BDF1 = { <span class="st">"Nom"</span>:<span class="st">"BDF1=EI"</span>, <span class="st">"p"</span>:<span class="dv">1</span>, <span class="st">"aa"</span>:[<span class="dv">1</span>], <span class="st">"bb"</span>:[<span class="dv">0</span>], <span class="st">"bm1"</span>:<span class="dv">1</span>  }
polyCarIMPL(BDF1)
Astabilite(BDF1)

$\displaystyle \varrho(r)=r^{2} - r$

$\displaystyle \sigma(r)=r^{2}$

Code

BDF2 = { <span class="st">"Nom"</span>:<span class="st">"BDF2"</span>, <span class="st">"p"</span>:<span class="dv">1</span>, <span class="st">"aa"</span>:[sp.Rational(<span class="dv">4</span>,<span class="dv">3</span>),<span class="op">-</span>sp.Rational(<span class="dv">1</span>,<span class="dv">3</span>)], <span class="st">"bb"</span>:[<span class="dv">0</span>], <span class="st">"bm1"</span>:sp.Rational(<span class="dv">2</span>,<span class="dv">3</span>) }
polyCarIMPL(BDF2)
Astabilite(BDF2)

$\displaystyle \varrho(r)=r^{2} - \frac{4 r}{3}$

$\displaystyle \sigma(r)=\frac{2 r^{2}}{3}$

Code

BDF3 = { <span class="st">"Nom"</span>:<span class="st">"BDF3"</span>, <span class="st">"p"</span>:<span class="dv">2</span>, <span class="st">"aa"</span>:[sp.Rational(<span class="dv">18</span>,<span class="dv">11</span>),<span class="op">-</span>sp.Rational(<span class="dv">9</span>,<span class="dv">11</span>),sp.Rational(<span class="dv">2</span>,<span class="dv">11</span>)], <span class="st">"bb"</span>:[<span class="dv">0</span>], <span class="st">"bm1"</span>:sp.Rational(<span class="dv">6</span>,<span class="dv">11</span>)  }
#polyCarIMPL(BDF3)
Astabilite(BDF3)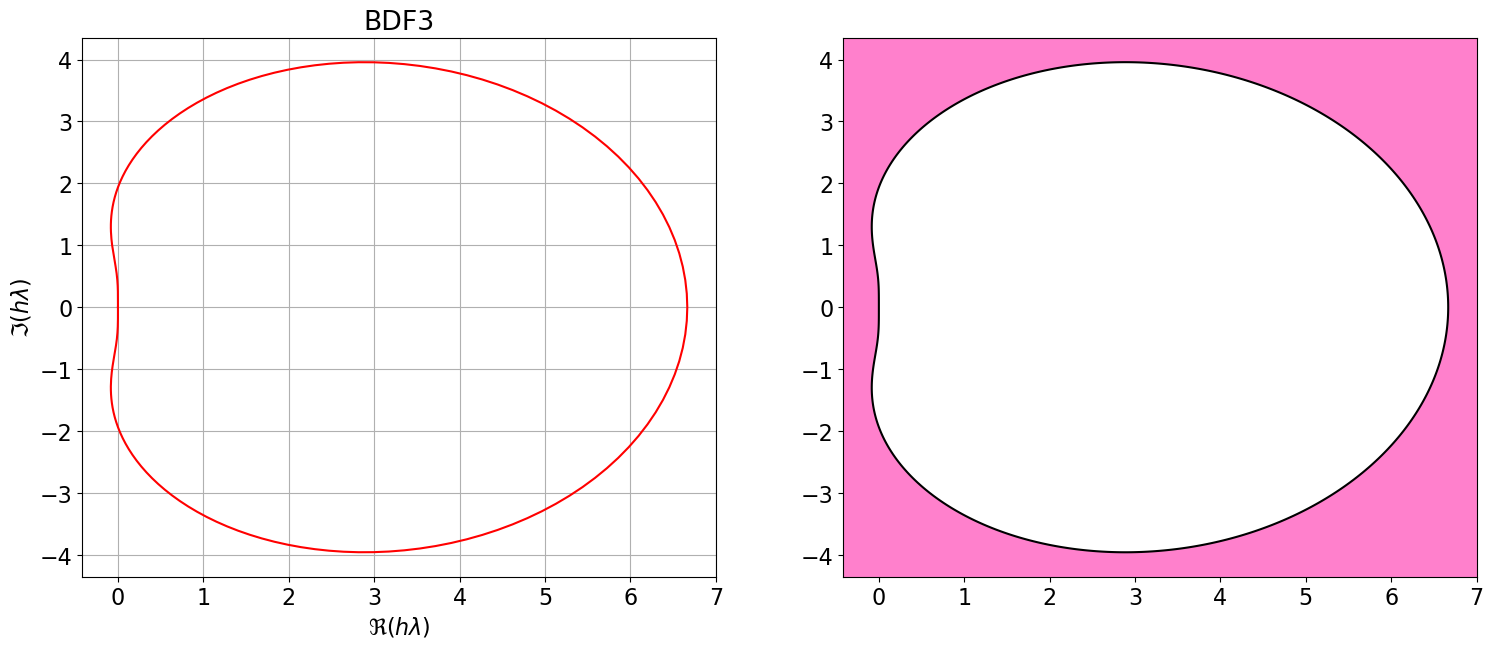

Code

BDF4 = { <span class="st">"Nom"</span>:<span class="st">"BDF4"</span>, <span class="st">"p"</span>:<span class="dv">3</span>, <span class="st">"aa"</span>:[sp.Rational(<span class="dv">48</span>,<span class="dv">25</span>),<span class="op">-</span>sp.Rational(<span class="dv">36</span>,<span class="dv">25</span>),sp.Rational(<span class="dv">16</span>,<span class="dv">25</span>),<span class="op">-</span>sp.Rational(<span class="dv">3</span>,<span class="dv">25</span>)], <span class="st">"bb"</span>:[<span class="dv">0</span>], <span class="st">"bm1"</span>:sp.Rational(<span class="dv">12</span>,<span class="dv">25</span>)  }
# polyCarIMPL(BDF4)
Astabilite(BDF4)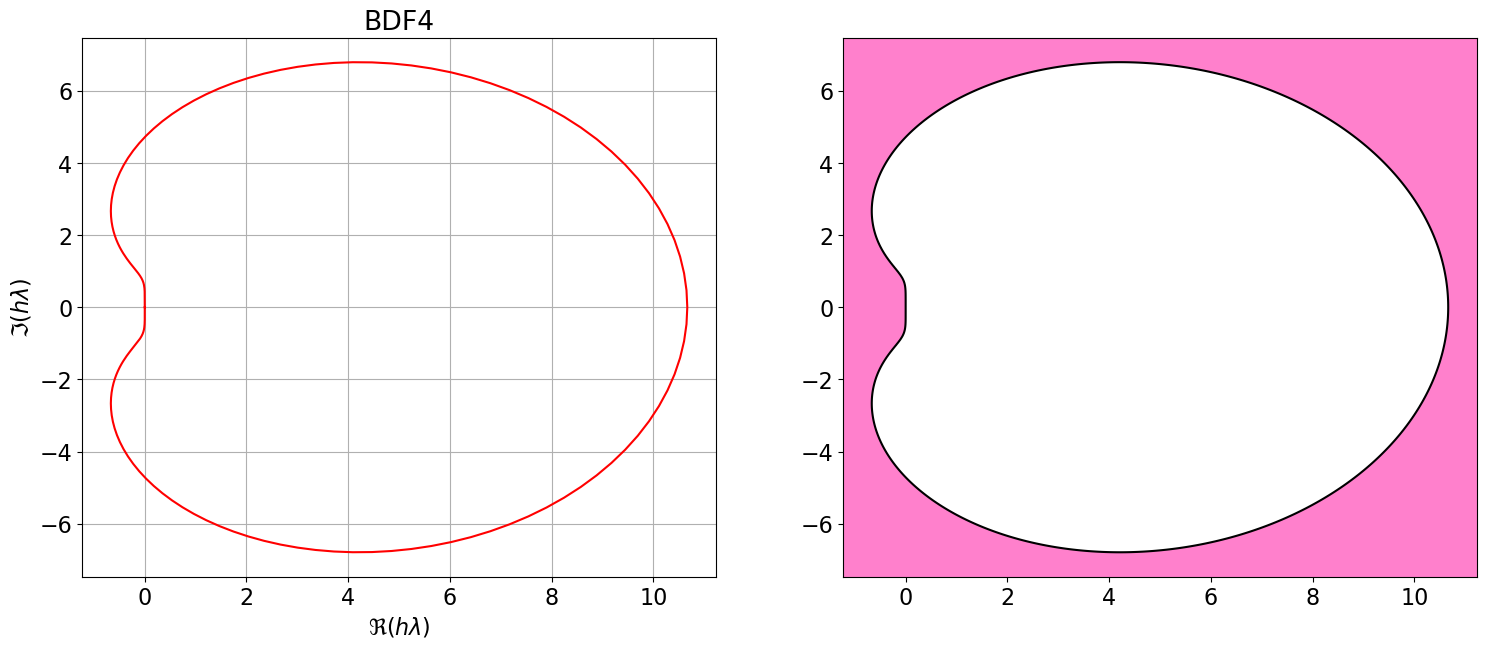

Code

BDF5 = { <span class="st">"Nom"</span>:<span class="st">"BDF5"</span>, <span class="st">"p"</span>:<span class="dv">4</span>, <span class="st">"aa"</span>:[sp.Rational(<span class="dv">300</span>,<span class="dv">137</span>),<span class="op">-</span>sp.Rational(<span class="dv">300</span>,<span class="dv">137</span>),sp.Rational(<span class="dv">200</span>,<span class="dv">137</span>),<span class="op">-</span>sp.Rational(<span class="dv">75</span>,<span class="dv">137</span>),sp.Rational(<span class="dv">12</span>,<span class="dv">137</span>)], <span class="st">"bb"</span>:[<span class="dv">0</span>], <span class="st">"bm1"</span>:sp.Rational(<span class="dv">60</span>,<span class="dv">137</span>) }
# polyCar(BDF5)
Astabilite(BDF5)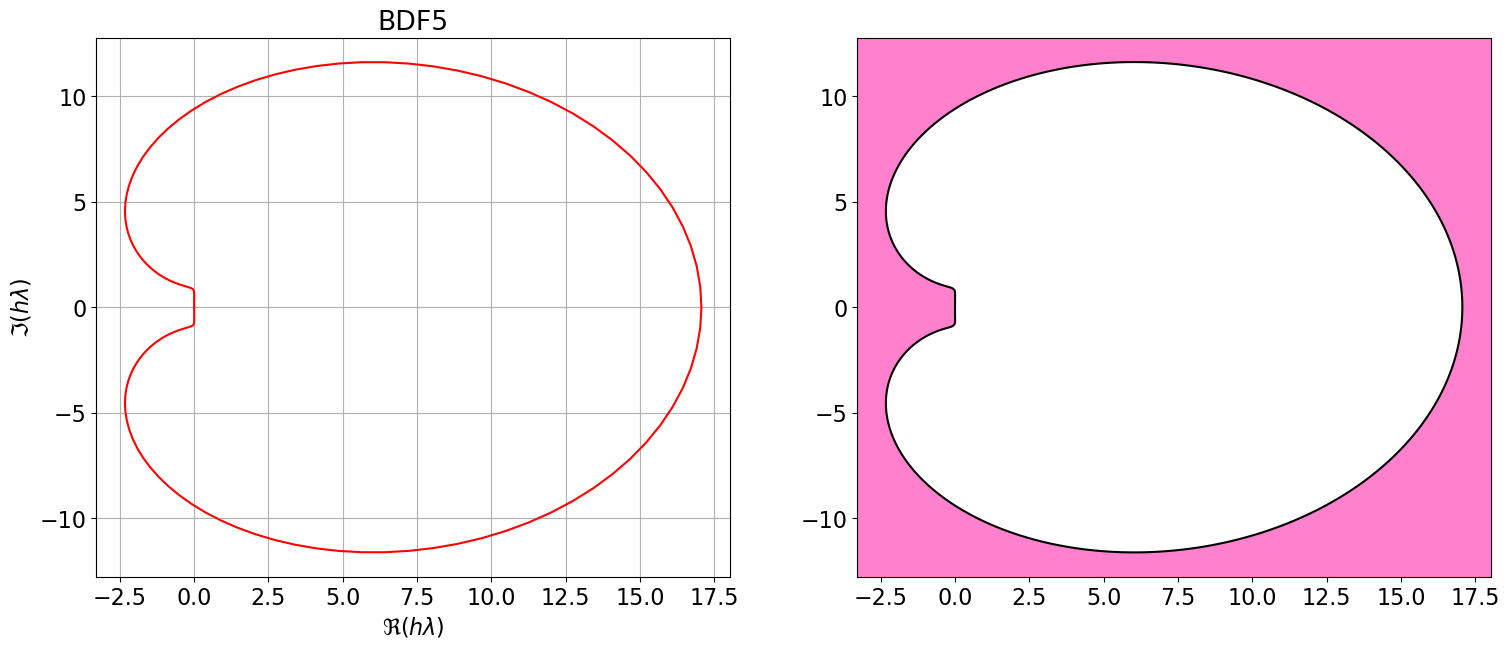

Code

BDF6 = { <span class="st">"Nom"</span>:<span class="st">"BDF6"</span>, <span class="st">"p"</span>:<span class="dv">5</span>, <span class="st">"aa"</span>:[sp.Rational(<span class="dv">120</span>,<span class="dv">49</span>),<span class="op">-</span>sp.Rational(<span class="dv">150</span>,<span class="dv">49</span>),sp.Rational(<span class="dv">400</span>,<span class="dv">147</span>),<span class="op">-</span>sp.Rational(<span class="dv">75</span>,<span class="dv">49</span>),sp.Rational(<span class="dv">24</span>,<span class="dv">49</span>),<span class="op">-</span>sp.Rational(<span class="dv">10</span>,<span class="dv">147</span>)], <span class="st">"bb"</span>:[<span class="dv">0</span>], <span class="st">"bm1"</span>:sp.Rational(<span class="dv">20</span>,<span class="dv">49</span>)  }
# polyCar(BDF6)
Astabilite(BDF6)

Retour au sommet

Méthode	Formule	\(a_0\)	\(b_{-1}\)	\(b_0\)
Euler explicite	\(u_{n+1}=u_n+h\varphi(t_n,u_n)\)	1	0	1
Euler implicite	\(u_{n+1}=u_n+h\varphi(t_{n+1},u_{n+1})\)	1	1	0
Crank-Nicolson	\(u_{n+1}=u_n+\frac{h}{2}(\varphi(t_n,u_n)+\varphi(t_{n+1},u_{n+1}))\)	1	\(\frac{1}{2}\)	\(\frac{1}{2}\)

Méthode	Formule	\(a_0\)	\(b_{-1}\)	\(b_0\)	\(\varrho(r)\)	\(\sigma(r)\)
Euler explicite	\(u_{n+1}=u_n+h\varphi(t_n,u_n)\)	1	0	1	\(r-1\)	\(1\)
Euler implicite	\(u_{n+1}=u_n+h\varphi(t_{n+1},u_{n+1})\)	1	1	0	\(r-1\)	\(r\)
Crank-Nicolson	\(u_{n+1}=u_n+\frac{h}{2}(\varphi(t_n,u_n)+\varphi(t_{n+1},u_{n+1}))\)	1	\(\frac{1}{2}\)	\(\frac{1}{2}\)	\(r-1\)	\(\frac{1}{2}r+\frac{1}{2}\)

Méthode	\(p\)	\(\varrho(r)\)	\(\sigma(r)\)
\(\text{AB}_q\) ou \(\text{AM}_q\)	\(q-1\)	\(r^{q+1}-r^{q}=r^{q}(r-1)\)	-
\(\text{N}_q\) ou \(\text{MS}_q\)	\(q-1\)	\(r^{q+1}-r^{q-1}=r^{q-1}(r^2-1)\)	-
\(\text{BDF}_2\)	\(q-1\)	\((r-1)\left(r-\frac{1}{3}\right)\)	\(\frac{2}{3}\)

Schéma	Type	Ordre maximal prévu par la barrière	Ordre réel \(\omega\)	Remarque
EE	Explicite	\(q=1\)	1	-
\(\text{AB}_2\)	Explicite	\(q=2\)	2	-
EI	Implicite, \(q\) impair	\(q+1 = 2\)	1	Non optimal : ordre réel \(1\), inférieur à l’ordre maximal \(2\)
CN	Implicite, \(q\) impair	\(q+1 = 2\)	2	-
\(\text{AM}_2\)	Implicite, \(q\) pair	\(q+2 = 4\)	3	Non optimal : ordre réel \(3\), inférieur à l’ordre maximal \(4\)
\(\text{MS}_2\)	Implicite, \(q\) pair	\(q+2 = 4\)	4	-

1 Rappels

1.1 Remarques

1.2 Les méthodes que nous avons vues jusqu’à présent sont des méthodes multipas ?

2 Polynômes caractéristiques

3 Convergence d’un schéma multipas linéaire

3.1 1️⃣ Consistance

3.2 2️⃣ Zéro-stabilité

3.3 3️⃣ Ordre de convergence maximale d’une méthode multipas linéaire

4 A-stabilité (dans \(\mathbb{C}\))

5 Exercice de synthèse : consistance, zéro-stabilité et A-stabilité des schémas EE, EI, CN

6 Propriétés des schémas Prédicteur-Correcteur basés sur les méthodes multi-pas

7 Méthodes cycliques composites : comment surmonter les limites de Dahlquist

8 Affichage des régions de A-stabilité

8.1 Régions de A-stabilité des méthodes d’Adams-Bashforth et d’Adams-Moulton

8.2 Régions de A-stabilité des méthodes BDF

8.3 Annexe : comment tracer les régions de A-stabilité ?