Premières manipulations avec Pandas

1 Exercice : premières manipulations de Series

• Construire la Series suivante :

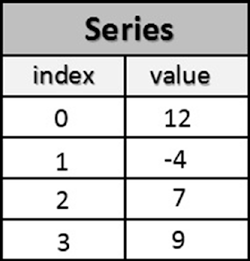
• Modifier la valeur de value à 10 pour l’élément en position 3.
• Afficher les éléments avec value supérieur à 5.
• Modifier la valeur de value à 0 pour les éléments avec un value inférieur à 5.
• Ajouter un élément avec un value de 3.5 à la Serie (cet élément doit avoir un label différent).
• Modifier les indices de la Serie pour qu’ils soient des lettres de l’alphabet.

import pandas as pd

# help(pd.Series)

# creation et affichage de la serie
# s = pd.Series([12, -4, 7, 9])
s = pd.Series(data=[12, -4, 7, 9])
s

0    12
1    -4
2     7
3     9
dtype: int64

# affichage des valeurs de la serie
s.values

array([12, -4,  7,  9])

# modification de la valeur de l'element d'indice 3
# s[3] = 10      # ambiguïté possible entre position et étiquette
# s.iloc[3] = 10 # modification par position
s.loc[3] = 10    # modification par étiquette
s

0    12
1    -4
2     7
3    10
dtype: int64

# filtre sur les valeurs de la serie
mask = s > 5 # création du masque
display(mask) # affichage du masque = c'est une serie de booléens
display(s[mask]) # affichage des valeurs filtrées

0     True
1    False
2     True
3     True
dtype: bool

0    12
2     7
3    10
dtype: int64

# filtre sur les valeurs de la serie et modification des valeurs
s[ s<5 ] = 0
s

0    12
1     0
2     7
3    10
dtype: int64

# display(s)
# s[len(s)] = 100
# display(s)

# Ajout d'une valeur à la serie
# 
# VISION NUMPY
# Concatenantion de deux series dont une contenant une seule valeur

# # L = pd.Series([3.5])
# # # s = pd.concat( [s,L] ) # PB !!!! deux fois le même index
# # s = pd.concat( [s,L] , ignore_index=True)
# # display(s)

# # Autre idée :
# L = pd.Series(data=[3.5], index=[len(s)])
# s = pd.concat( [s,L] )
# display(s)



# VISION DICTIONNAIRE
s[len(s)] = 100
display(s)

0     12
1      0
2      7
3     10
4    100
dtype: int64

# changement des indices
s.index = ['a', 'b', 'c', 'd', 'e']
s

a     12
b      0
c      7
d     10
e    100
dtype: int64

2 Exercice : premières manipulations de DataFrame

• Construire le DataFrame suivant :

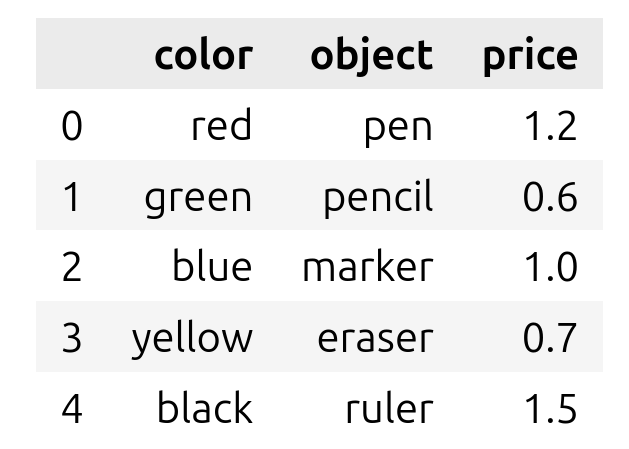
• Afficher les lignes correspondant aux objets dont le prix est supérieur ou égale à 1.
• Modifier le prix de l’objet “eraser” pour le passer à 0.2.

La construction du DataFrame peut se faire en deux étapes. D’abord, on crée un dictionnaire avec les données (colonne par colonne), puis on crée le DataFrame à partir de ce dictionnaire.

import pandas as pd

# un dictionaire de listes, chaque liste representant une colonne
data = {'color' :  ['red', 'green', 'blue', 'yellow', 'black'],
        'object' : ['pen', 'pencil', 'marker', 'eraser', 'ruler'],
        'price' :  [1.2, 0.6, 1.0, 0.7, 1.5]}

df = pd.DataFrame(data)
df

	color	object	price
0	red	pen	1.2
1	green	pencil	0.6
2	blue	marker	1.0
3	yellow	eraser	0.7
4	black	ruler	1.5

On va séléctionner les lignes du DataFrame en utilisant un masque :

mask = (df['price'] > 1.0) 
df[ mask ] # application du masque à toutes les colonnes

	color	object	price
0	red	pen	1.2
4	black	ruler	1.5

# pour comprendre
mask
# Dans la sortie on voit l'indice de la ligne et un booléen qui indique si la condition est vraie ou fausse pour cette ligne

0     True
1    False
2    False
3    False
4     True
Name: price, dtype: bool

On va modifier la valeur d’une cellule : avec .loc on peut accéder à une cellule en utilisant les indices de la ligne et de la colonne. Pour trouver l’indice de la ligne correspondant à l’objet “eraser”, on peut utiliser un masque.

label_de_la_ligne = (df['object']=='eraser')
label_de_la_colonne = 'price'
df.loc[ label_de_la_ligne, label_de_la_colonne ] = 0.2
df

	color	object	price
0	red	pen	1.2
1	green	pencil	0.6
2	blue	marker	1.0
3	yellow	eraser	0.2
4	black	ruler	1.5

Pour comprendre:

df['object']=='eraser'

0    False
1    False
2    False
3     True
4    False
Name: object, dtype: bool

df.loc[ df['object']=='eraser', : ]

	color	object	price
3	yellow	eraser	0.2

3 Exercice : dict de dict en DataFrame

Transformer en dataframe le dictionnaire de dictionnaires suivant:

pop = {'Nevada': {2001: 2.4, 2002: 2.9},
       'Ohio'  : {2000: 1.5, 2001: 1.7, 2002: 3.6}}

Une autre forme courante de données est un dictionnaire qui contient plusieurs autres dictionnaires. Si le dictionnaire priciapl est passé au DataFrame, pandas interprétera les clés du dictionnaire extérieur comme étant les colonnes, et les clés intérieures comme étant les indices des lignes :

import pandas as pd

pop = {'Nevada': {2001: 2.4, 2002: 2.9},
       'Ohio'  : {2000: 1.5, 2001: 1.7, 2002: 3.6}}

pd.DataFrame(data=pop)

	Nevada	Ohio
2001	2.4	1.7
2002	2.9	3.6
2000	NaN	1.5

4 Exercice : regression linéaire

Source : problème 32 de “Python & Pandas et les 36 problèmes de Data Science”, Frédéric Bro et Chantal Remy

Dans The Song of Insects de George W. Pierce, on trouve des données sur la fréquence par minute des stridulations (le son produit par les frottements des ailes) de la cigale Tibicen linnei et la température (en degré Fahrenheit) à laquelle les stridulations ont été enregistrées.

Les données sont les suivantes \[ \begin{array}{|c|c|} \hline \text{Fréquence des stridulations (x)} & \text{Température (y)} \\ \hline 20.0 & 88.6 \\ 20.8 & 71.6 \\ 22.4 & 93.3 \\ 23.3 & 84.3 \\ 26.7 & 93.4 \\ 26.8 & 93.3 \\ 27.4 & 87.6 \\ 28.3 & 84.5 \\ 33.4 & 80.6 \\ 35.9 & 75.2 \\ 36.0 & 85.5 \\ 36.0 & 80.6 \\ 36.8 & 82.6 \\ 37.1 & 89.4 \\ 37.2 & 88.0 \\ 39.6 & 89.0 \\ 40.3 & 83.5 \\ 42.4 & 82.6 \\ 47.6 & 80.6 \\ \hline \end{array} \]

Objectif : établir par régression linéaire la relation entre la fréquence des stridulations et la température. Autrement dit, si on note \(x\) la fréquence des stridulations et \(y\) la température, on cherche deux nombres \(a\) et \(b\) tels que \(y\) soit approximativement égale à \(ax+ b\). Cela s’obtient par la méthode des moindres carrés qui consiste à minimiser la somme des carrés des écarts entre les valeurs observées et les valeurs prédites par le modèle : \[ (a,b)\qquad\text{tels que}\qquad\sum_{i=1}^n (y_i - (a \times x_i + b))^2 \quad\text{minimale.} \]

Les coefficients de la droite de régression peuvent être obtenus avec la fonction polyfit de numpy. Cette fonction prend en argument les listes des abscisses et des ordonnées des points et le degré du polynôme à ajuster. Pour une régression linéaire, on utilise un polynôme de degré 1. Elle renvoie les coefficients du polynôme dans l’ordre décroissant des puissances :

import numpy as np
coeffs = np.polyfit(x=x_pt, y=y_pt, deg=1)
droite = lambda x: coeffs[0] * x + coeffs[1]

import pandas as pd
import numpy as np

M = np.array([  [14.39999962, 76.30000305],
                [14.69999981, 69.69999695],
                [15.        , 79.59999847],
                [15.39999962, 69.40000153],
                [15.5       , 75.19999695],
                [16.        , 71.59999847],
                [16.        , 80.59999847],
                [16.20000076, 83.30000305],
                [17.        , 83.5       ],
                [17.10000038, 80.59999847],
                [17.10000038, 82.        ],
                [17.20000076, 82.59999847],
                [18.39999962, 84.30000305],
                [19.79999924, 93.30000305],
                [20.        , 88.59999847]])

df = pd.DataFrame(data=M)
df.columns = ['Nombre de stridulations par minute', 'Température']
df.sort_values(by='Nombre de stridulations par minute', inplace=True)
df

	Nombre de stridulations par minute	Température
0	14.400000	76.300003
1	14.700000	69.699997
2	15.000000	79.599998
3	15.400000	69.400002
4	15.500000	75.199997
5	16.000000	71.599998
6	16.000000	80.599998
7	16.200001	83.300003
8	17.000000	83.500000
9	17.100000	80.599998
10	17.100000	82.000000
11	17.200001	82.599998
12	18.400000	84.300003
13	19.799999	93.300003
14	20.000000	88.599998

x_points = df['Nombre de stridulations par minute']
y_points = df['Température']

a, b = np.polyfit(x_points, y_points, 1)

# La droite de regression a pour equation y = a*x + b
f = lambda x : a*x + b

# TEST : si un criquet stridule 19 fois par minute, la temperature prédite est
f(19) # idem que np.polyval([a, b], 19)

87.76310177442974

import matplotlib.pyplot as plt

plt.plot(x_points, y_points, 'o') # les points du nuage de points
xx = np.linspace(min(x_points), max(x_points), 101)
plt.plot(xx, [f(x) for x in xx]) # la droite de régression
plt.xlabel('Nombre de stridulations par minute')
plt.ylabel('Température')
plt.grid()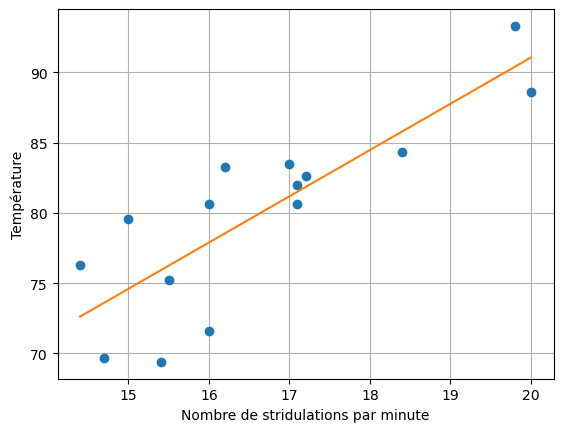

Seaborn permet de calculer et tracer directement la droite de régression avec la fonction regplot :

import seaborn as sns
sns.regplot(x='x', y='y', data=df)

Pour accéder à la documentation de la fonction regplot, on peut utiliser le point d’interrogation :

? sns.regplot

import seaborn as sns

sns.regplot(x='Nombre de stridulations par minute', y='Température', data=df, ci=None);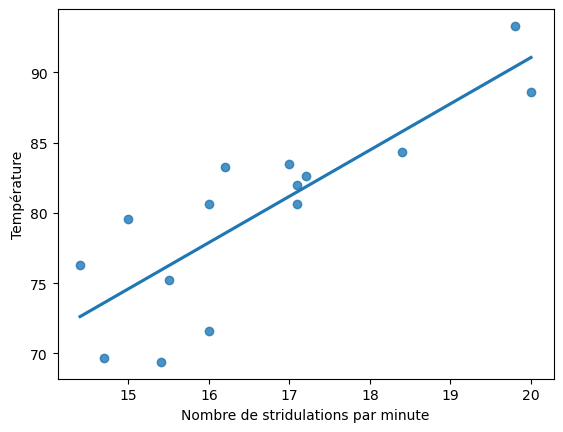

Rappel : la droite de regression passe par le point moyen des données. Vérifions cela ;

x_moy = np.mean(x_points)
y_moy = np.mean(y_points)

# La droite de regression passe par le point de coordonnées (x_moy, y_moy) ?
y_moy - f(x_moy)

-1.4210854715202004e-14

Rappel : la qualité de l’ajustement est souvent mesurée par le coefficient de corrélation linéaire \(r\) qui est compris entre -1 et 1. Plus \(r\) est proche de 1, plus la droite de régression est proche des points. \[ r = \frac{\sum_{i=1}^n (x_i - \bar{x})(y_i - \bar{y})}{\sqrt{\sum_{i=1}^n (x_i - \bar{x})^2}\sqrt{\sum_{i=1}^n (y_i - \bar{y})^2}} \]

# La droite de regression est-elle une bonne approximation ?
r = sum( (x_points-x_moy ) * (y_points-y_moy) ) / np.sqrt(sum( (x_points - x_moy)**2)) / np.sqrt(sum( (y_points - y_moy)**2))
r

0.8351437870311553