Loi de Benford et suspicion de fraudes aux présidentielles des USA en 2016

Auteur·rice

Gloria FACCANONI

Date de publication

26 novembre 2025

Source : problème 9 de “Python & Pandas et les 36 problèmes de Data Science”, Frédéric Bro et Chantal Remy

La loi de Benford est une loi empirique qui concerne la distribution des premiers chiffres significatifs dans de nombreux ensembles de données réels. Elle prédit que, dans de nombreux ensembles de données réels, le premier chiffre significatif suit une distribution logarithmique, c’est-à-dire que le chiffre 1 apparaît en premier 30% du temps, le chiffre 2 17,6% du temps, le chiffre 3 12,5% du temps, etc. Une loi analogue est valable pour le second chiffre significatif. De nos jours, pour vérifier l’authenticité des données, on peut vérifier si elles suivent la loi de Benford. Si ce n’est pas le cas, cela peut être un signe de fraude.

Lors des élections présidentielles américaines de 2016, des chercheurs ont appliqué la loi de Benford aux résultats des élections dans les différents États. Ils ont constaté que les résultats des élections dans certains États ne suivaient pas la loi de Benford et ont suggéré que cela pourrait être dû à des fraudes électorales. Ceci incita les candidats Hilary Clinton et Jill Stein à demander un comptage manuel dans certains comtés.

Dans cet exercice, vous allez vérifier si les résultats des élections dans les différents États des États-Unis en 2016 suivent la loi de Benford. Pour cela, vous allez utiliser les données des élections présidentielles américaines de 2016, disponibles dans le fichier benford_usa.csv.

Quelques liens pour en savoir plus sur la loi de Benford :

1 Exercice

  1. Loi de Benford
    Tracer la fréquence relative du deuxième chiffre significatif \(c\in\{0,1,\dots,9\}\) dans la représentation en base \(10\) prédite par la loi de Benford : \[ p(c) = \sum_{i=1}^9 \log_{10}\left(1+\frac{1}{10i+c}\right). \]

  2. Ouverture et sélection des données

    • Le fichier benford_usa.csv contient le nombre de voix remportées par trois candidats dans chaque district des États-Unis. Importer le fichier et analyser brièvement les données.
      Bonus : retrouver le résultat des élections en combinant avec le nombre de grands électeurs par État (cf. Wikipedia).
    • Ne garder ensuite que les lignes correspondant aux comtés du Michigan, de la Pennsylvanie et du Wisconsin. Parmi ces lignes, ne garder que celles où chaque candidat a obtenu plus de 10 voix. Ce sont ces données que nous allons analyser.

  3. Analyse des données
    En théorie, la répartition des fréquences du deuxième chiffre des nombres de voix suit la loi de Benford. Pour chaque candidat, vérifier si c’est le cas.

    • Calculer la fréquence du deuxième chiffre des nombres de voix pour chaque candidat et comparer avec la loi de Benford (créer un DataFrame où chaque ligne correspond à un chiffre et chaque colonne à un candidat ; ajouter une colonne pour les fréquences théoriques).
    • Afficher/visualiser la distribution de chaque colonne.

  4. Bonus : simulation pour la détection d’éventuelles anomalies
    Les graphes peuvent susciter des doutes quant à la régularité des résultats. Pour aller plus loin, introduire un indicateur synthétique pour résumer l’analyse.

    • Calculer la distance euclidienne entre la colonne théorique et la colonne observée pour chaque candidat.
    • Si l’indicateur est extrême, est-ce si rare ? Simuler \(10^4\) votations qui suivent la distribution théorique de Benford et vérifier si ce résultat est effectivement rare ou non.

Importation des bibliothèques nécessaires.

import pandas as pd
import numpy as np

import matplotlib.pyplot as plt
plt.style.use('bmh')
import seaborn as sns

2 Loi de Benford

La fonction théorique \(p\) qui donne la fréquence du second chiffre significatif dans la représentation en base \(10\) prédite par la loi de Benford est donnée par:
\[ p(c) = \sum_{i=1}^9 \log_{10}\left(1+\frac{1}{10i+c}\right). \]


# Fonction pour calculer la probabilité
p = lambda c : sum( [ np.log10( 1+1/(10*i+c)) for i in range( 1 , 10 ) ] ) 

# Générer les chiffres de 0 à 9
cc = np.arange(0,10) 

# Calculer les probabilités pour chaque valeur de cc
FB = [ p(c) for c in cc ]


# Affichage des résultats dans un DataFrame
df = pd.DataFrame({'Chiffre':cc,'Probabilité':FB})
# Transformer les valeurs en DataFrame et utiliser la première colonne comme index
df = df.set_index('Chiffre')  # Notez que set_index renvoie un nouveau DataFrame
display(df)

# Vérification que FB est normalisée
display(df['Probabilité'].sum())

# Tracer les résultats
sns.barplot(x='Chiffre',y='Probabilité',data=df);
Probabilité
Chiffre
0 0.119679
1 0.113890
2 0.108821
3 0.104330
4 0.100308
5 0.096677
6 0.093375
7 0.090352
8 0.087570
9 0.084997 
0.9999999999999997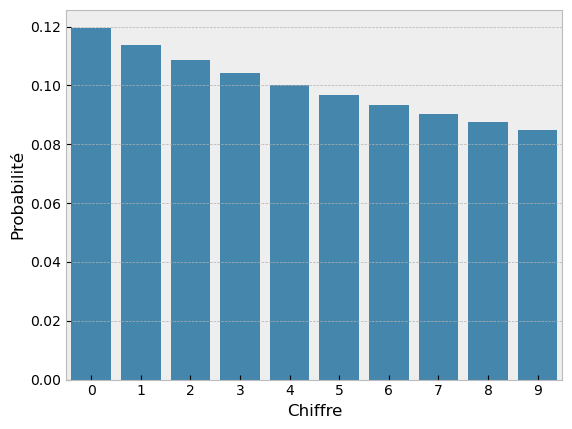

3 Ouverture et séléction des données

On importe les données à partir d’un fichier csv. Par défaut, le séparateur d’éléments est “,” ; dans ce fichier c’est “;”, il faut donc l’indiquer explicitement.

Tot = pd.read_csv('benford_usa.csv', sep=';')
# Tot.shape
Tot.info()
<class 'pandas.core.frame.DataFrame'>
RangeIndex: 3143 entries, 0 to 3142
Data columns (total 7 columns):
 #   Column   Non-Null Count  Dtype 
---  ------   --------------  ----- 
 0   State    3143 non-null   object
 1   ST       3143 non-null   object
 2   Fips     3143 non-null   int64 
 3   County   3143 non-null   object
 4   Trump    3143 non-null   int64 
 5   Clinton  3143 non-null   int64 
 6   Stein    3143 non-null   int64 
dtypes: int64(4), object(3)
memory usage: 172.0+ KB
Tot.head(10)
State ST Fips County Trump Clinton Stein
0 Georgia GA 13089 DeKalb County, Georgia 47531 239131 0
1 Texas TX 48487 Wilbarger County, Texas 3166 807 13
2 Virginia VA 51111 Lunenburg County, Virginia 3206 2226 25
3 Georgia GA 13297 Walton County, Georgia 31093 8279 0
4 North Carolina NC 37011 Avery County, North Carolina 6226 1670 0
5 North Carolina NC 37069 Franklin County, North Carolina 16320 12811 0
6 Michigan MI 26037 Clinton County, Michigan 21635 16490 379
7 Arkansas AR 5045 Faulkner County, Arkansas 29170 14525 507
8 North Carolina NC 37025 Cabarrus County, North Carolina 53224 35048 0
9 Idaho ID 16025 Camas County, Idaho 410 110 15

Les colonnes “ST”, “Fips” et “County” ne sont pas utiles pour notre analyse, on peut les supprimer.

Tot.drop(columns=['ST', 'Fips', 'County'],inplace=True)
Tot
State Trump Clinton Stein
0 Georgia 47531 239131 0
1 Texas 3166 807 13
2 Virginia 3206 2226 25
3 Georgia 31093 8279 0
4 North Carolina 6226 1670 0
... ... ... ... ...
3138 Tennessee 9525 2425 36
3139 Michigan 224589 176238 3886
3140 West Virginia 3516 1315 47
3141 North Carolina 6225 1585 0
3142 Maryland 7938 5695 94

3143 rows × 4 columns

Combien d’états sont dans le fichier ? Lesquels ? Affichons la liste des états (sans doublons):

Tot['State'].nunique()
51
df_tmp = Tot['State'].unique()
sorted(df_tmp.tolist())
['Alabama',
 'Alaska',
 'Arizona',
 'Arkansas',
 'California',
 'Colorado',
 'Connecticut',
 'Delaware',
 'District of Columbia',
 'Florida',
 'Georgia',
 'Hawaii',
 'Idaho',
 'Illinois',
 'Indiana',
 'Iowa',
 'Kansas',
 'Kentucky',
 'Louisiana',
 'Maine',
 'Maryland',
 'Massachusetts',
 'Michigan',
 'Minnesota',
 'Mississippi',
 'Missouri',
 'Montana',
 'Nebraska',
 'Nevada',
 'New Hampshire',
 'New Jersey',
 'New Mexico',
 'New York',
 'North Carolina',
 'North Dakota',
 'Ohio',
 'Oklahoma',
 'Oregon',
 'Pennsylvania',
 'Rhode Island',
 'South Carolina',
 'South Dakota',
 'Tennessee',
 'Texas',
 'Utah',
 'Vermont',
 'Virginia',
 'Washington',
 'West Virginia',
 'Wisconsin',
 'Wyoming']

Combien de voix ont été obtenues par chaque candidat au total ?

# On affiche le nombre total de votes pour chaque candidat, i.e. la somme des colonnes Trump, Clinton et Stein
cols = ['Trump','Clinton','Stein'] 

pour_affichage = pd.DataFrame( Tot[cols].sum().sort_values(ascending=False),columns=['Nombre de votes'])
pour_affichage['Pourcentage'] = pour_affichage / pour_affichage.sum() * 100

# pour un affichage plus joli
pour_affichage = pour_affichage.style.format({'Pourcentage':'{:.2f} %'})
pour_affichage
  Nombre de votes Pourcentage
Clinton 62426228 50.02 %
Trump 61064602 48.93 %
Stein 1311595 1.05 %

4 Bonus : pourquoi une fraude éventuelle dans ces trois états aurait changé le résultat de l’élection ?

Aux USA, ce n’est pas la majorité qui gagne mais le candidat qui obtient le plus de grands électeurs. Clinton a obtenu plus de voix que Trump mais c’est ce dernier qui a été élu. En effet, chaque État a un nombre de grands électeurs qui lui est attribué et le candidat qui remporte la majorité des voix dans un État obtient tous les grands électeurs de cet État.

Voici le bilan des voix puis des grands électeurs obtenus par chaque candidat :

# Agréger les votes par état
votes_by_state = Tot.pivot_table(index='State', values=['Trump', 'Clinton', 'Stein'], aggfunc='sum')
votes_by_state
Clinton Stein Trump
State
Alabama 718084 9287 1306925
Alaska 0 0 0
Arizona 936250 25255 1021154
Arkansas 378729 9837 677904
California 7362490 220312 3916209
Colorado 1212209 33147 1137455
Connecticut 884432 22793 668266
Delaware 235581 6100 185103
District of Columbia 260223 3995 11553
Florida 4485745 64019 4605515
Georgia 1837300 0 2068623
Hawaii 266827 12727 128815
Idaho 189677 8464 407199
Illinois 2977498 74112 2118179
Indiana 1031953 0 1556220
Iowa 650790 11119 798923
Kansas 414788 22698 656009
Kentucky 628834 13913 1202942
Louisiana 779535 14018 1178004
Maine 354873 14075 334838
Maryland 1497951 31839 873646
Massachusetts 1964768 46910 1083069
Michigan 2268193 50700 2279805
Minnesota 1366676 36957 1322891
Mississippi 462001 3580 678457
Missouri 1054889 25086 1585753
Montana 174521 7669 274120
Nebraska 273858 8346 485819
Nevada 537753 0 511319
New Hampshire 348521 6416 345789
New Jersey 2021756 35949 1535513
New Mexico 380724 9729 315875
New York 4143874 99895 2640570
North Carolina 2162074 0 2339603
North Dakota 93526 3769 216133
Ohio 2317001 44310 2771984
Oklahoma 419788 0 947934
Oregon 934631 45132 742506
Pennsylvania 2844705 48912 2912941
Rhode Island 249902 6155 179421
South Carolina 849469 12917 1143611
South Dakota 114938 0 227460
Tennessee 867110 15919 1517402
Texas 3867816 71307 4681590
Utah 274188 7695 452086
Vermont 178179 6748 95053
Virginia 1916845 27272 1731156
Washington 1610524 51066 1129120
West Virginia 187457 8000 486198
Wisconsin 1380823 30934 1403694
Wyoming 55949 2512 174248

On constate que, pour l’Alaska, les résultats des trois candidats (Trump, Clinton et Stein) sont tous à 0 ; cela signifie qu’il n’y a pas de votes enregistrés pour cet État dans le fichier. Y a‑t‑il d’autres États pour lesquels les résultats sont manquants ? Si oui, lesquels ? Pour détecter ces États, on peut filtrer les lignes où les totaux de votes pour ces candidats sont égaux à zéro.

# Filtrer les lignes où les votes sont tous à zéro pour Trump, Clinton et Stein
# On utilise sum(axis=1) qui calcule la somme des votes pour chaque ligne (chaque état)
mask = votes_by_state[['Trump', 'Clinton', 'Stein']].sum(axis=1) == 0
states_with_no_votes = votes_by_state[mask]
# Afficher les états avec 0 votes
states_with_no_votes
Clinton Stein Trump
State
Alaska 0 0 0

Nous constatons que les résultats pour 1 état sont absents dans notre jeu de données. Cependant, nous poursuivrons l’analyse en supposant que toutes les données nécessaires sont présentes, sans tenir compte de cette omission.

Ajoutons maintenant le nombre de grands électeurs par état. Pour cela, nous allons utiliser un dictionnaire qui contient le nombre de grands électeurs par état.

# Dictionnaire des grands électeurs par état en 2016
electoral_votes = {
    "Georgia": 16,
    "Texas": 38,
    "Virginia": 13,
    "North Carolina": 15,
    "Michigan": 16,
    "Arkansas": 6,
    "Idaho": 4,
    "Florida": 29,
    "Tennessee": 11,
    "Kentucky": 8,
    "Alabama": 9,
    "Colorado": 9,
    "Missouri": 10,
    "Ohio": 18,
    "Pennsylvania": 20,
    "South Dakota": 3,
    "Louisiana": 8,
    "Wisconsin": 10,
    "Minnesota": 10,
    "Indiana": 11,
    "Maryland": 10,
    "Kansas": 6,
    "New York": 29,
    "Mississippi": 6,
    "North Dakota": 3,
    "Iowa": 6,
    "California": 55,
    "Wyoming": 3,
    "New Mexico": 5,
    "Montana": 3,
    "Utah": 6,
    "Oklahoma": 7,
    "Alaska": 3,
    "Oregon": 7,
    "Illinois": 20,
    "Hawaii": 4,
    "South Carolina": 9,
    "West Virginia": 5,
    "Arizona": 11,
    "Maine": 4,
    "New Jersey": 14,
    "Connecticut": 7,
    "Nebraska": 5,
    "Washington": 12,
    "Nevada": 6,
    "Massachusetts": 11,
    "Rhode Island": 4,
    "New Hampshire": 4,
    "Delaware": 3,
    "Vermont": 3,
    "District of Columbia": 3,
}


# Ajouter les grands électeurs au DataFrame
votes_by_state['ElectoralVotes'] = electoral_votes
votes_by_state.head()
Clinton Stein Trump ElectoralVotes
State
Alabama 718084 9287 1306925 9
Alaska 0 0 0 3
Arizona 936250 25255 1021154 11
Arkansas 378729 9837 677904 6
California 7362490 220312 3916209 55 
# Trouver le gagnant pour chaque état
votes_by_state['Winner'] = votes_by_state[['Trump', 'Clinton', 'Stein']].idxmax(axis=1)
votes_by_state.head()
Clinton Stein Trump ElectoralVotes Winner
State
Alabama 718084 9287 1306925 9 Trump
Alaska 0 0 0 3 Trump
Arizona 936250 25255 1021154 11 Trump
Arkansas 378729 9837 677904 6 Trump
California 7362490 220312 3916209 55 Clinton

On regarde juste les trois lignes associées aux états du Michigan, de Pennsylvanie et du Wisconsin.

votes_by_state.loc[['Michigan', 'Wisconsin', 'Pennsylvania']]
Clinton Stein Trump ElectoralVotes Winner
State
Michigan 2268193 50700 2279805 16 Trump
Wisconsin 1380823 30934 1403694 10 Trump
Pennsylvania 2844705 48912 2912941 20 Trump 
# Résultats finaux
final_results = votes_by_state.pivot_table(index='Winner', values='ElectoralVotes', aggfunc='sum')

# Ajouter le nombre de votes pour chaque candidat, le pourcentage de grands électeurs et le pourcentage de votes
final_results.insert(0, 'Votes', votes_by_state[['Trump', 'Clinton', 'Stein']].sum())
final_results.insert(1, 'PercentageVotes' , final_results['Votes'] / final_results['Votes'].sum() * 100)
final_results['PercentageElectoralVotes'] =  final_results['ElectoralVotes'] / final_results['ElectoralVotes'].sum() * 100
final_results
Votes PercentageVotes ElectoralVotes PercentageElectoralVotes
Winner
Clinton 62426228 50.551307 233 43.30855
Trump 61064602 49.448693 305 56.69145

Sur Wikipedia on peut trouver les résultats suivants pour les élections :

  • Hillary Clinton : 65 853 514 voix, 232 grands électeurs
  • Donald Trump : 62 984 828 voix, 306 grands électeurs

Nos données ne sont donc pas complètes.

On voit que Trump a obtenu 305 grands électeurs contre 233 pour Clinton. Il a donc été élu président des USA. Cependant, si les résultats dans les états du Michigan, de Pennsylvanie et du Wisconsin avaient été différents, Clinton aurait obtenu plus de grands électeurs (et Trump moins). Aurait-elle été élue ?

# Calcul de la somme des grands électeurs des états impliqués dans la triche éventuelle
si_triche_verifiee = electoral_votes['Michigan'] + electoral_votes['Wisconsin'] + electoral_votes['Pennsylvania']

# Ajuster les résultats de Trump et Clinton
new_Trump = final_results.loc['Trump','ElectoralVotes'] - si_triche_verifiee  # Déduire les grands électeurs pour Trump
new_Clinton = final_results.loc['Clinton','ElectoralVotes'] + si_triche_verifiee  # Ajouter les grands électeurs à Clinton

# Afficher les résultats ajustés
new_Trump, new_Clinton
(259, 279)

5 Sélection des données dans les États du Michigan, de la Pennsylvanie et du Wisconsin

Nous allons examiner les données relatives aux États du Michigan, du Wisconsin et de la Pennsylvanie. Nous nous intéressons aux comtés où chaque candidat a obtenu plus de 10 voix.

mask1 = (Tot['State'] == 'Michigan') | (Tot['State'] == 'Wisconsin') | (Tot['State'] == 'Pennsylvania') 
# mask1 = Tot['State'].isin(['Michigan', 'Wisconsin', 'Pennsylvania'])

mask2 = (Tot['Trump'] >= 10) & (Tot['Clinton'] >= 10) & (Tot['Stein'] >= 10)

# Nouveau DataFrame avec les lignes sélectionnées
Sel = Tot[mask1 & mask2].copy() 
Sel
State Trump Clinton Stein
6 Michigan 21635 16490 379
12 Michigan 2158 1156 49
20 Pennsylvania 22676 6849 136
26 Wisconsin 17310 18524 583
33 Wisconsin 31044 17391 449
... ... ... ... ...
3057 Wisconsin 39010 26476 641
3090 Pennsylvania 257488 363017 5021
3105 Wisconsin 46620 42506 834
3125 Michigan 7228 3973 116
3139 Michigan 224589 176238 3886

220 rows × 4 columns

Combien de bureaux de vote sont concernés par ces critères ?

nb_bureaux = Sel.shape[0]
nb_bureaux
220

Combien de voix ont été obtenues par chaque candidat au total dans ces trois états ?

cols = ['Trump','Clinton','Stein'] 

pour_affichage = pd.DataFrame( Sel[cols].sum().sort_values(ascending=False),columns=['Nombre de votes'])
pour_affichage['Pourcentage'] = pour_affichage / pour_affichage.sum() * 100

# pour un affichage plus joli
pour_affichage = pour_affichage.style.format({'Pourcentage':'{:.2f} %'})
pour_affichage
  Nombre de votes Pourcentage
Trump 6594676 49.89 %
Clinton 6492249 49.12 %
Stein 130535 0.99 %

6 Analyse des données

Combien de votes aux total par candidat dans ces trois états ?

# Sel_sum = Sel.groupby('State')[cols].sum()
Sel_sum = Sel.pivot_table(index='State',values=cols,aggfunc='sum')
Sel_sum
Clinton Stein Trump
State
Michigan 2268193 50700 2279805
Pennsylvania 2844236 48908 2911446
Wisconsin 1379820 30927 1403425 
# Pourcentage de la distribution des votes dans chaque état
Sel_sum.div(Sel_sum.sum(axis=1), axis=0) * 100
Clinton Stein Trump
State
Michigan 49.322504 1.102486 49.575010
Pennsylvania 48.999774 0.842575 50.157651
Wisconsin 49.031118 1.098973 49.869908

Nous allons ajouter, pour chaque candidat, une colonne contenant le deuxième chiffre du nombre de voix :

for candidat in ["Trump", "Clinton", "Stein"]:
    Sel.loc[:, candidat + '_2chiffre'] = Sel[candidat].apply(lambda x: int(str(x)[1]))    

Sel.head()
State Trump Clinton Stein Trump_2chiffre Clinton_2chiffre Stein_2chiffre
6 Michigan 21635 16490 379 1 6 7
12 Michigan 2158 1156 49 1 1 9
20 Pennsylvania 22676 6849 136 2 8 3
26 Wisconsin 17310 18524 583 7 8 8
33 Wisconsin 31044 17391 449 1 7 4

On crée un DataFrame avec l’histogramme des secondes chiffres par candidat. Autrement dit, on compte le nombre de fois où chaque chiffre est apparu en deuxième position dans les nombres de votes.

Pour cela on utilise apply qui applique une fonction donnée (ici, pd.Series.value_counts) à chaque colonne du DataFrame résultant. La fonction pd.Series.value_counts compte les occurrences uniques des valeurs dans une série (ici une colonne) et renvoie une série dont les indices sont les valeurs uniques présentes dans la colonne d’origine. Ces valeurs sont triées par défaut en ordre décroissant de fréquence.

# Première méthode
# Trump_histo = Sel['Trump_2chiffre'].value_counts()
# Clinton_histo = Sel['Clinton_2chiffre'].value_counts()
# Stein_histo = Sel['Stein_2chiffre'].value_counts()

Trump_histo = Sel['Trump_2chiffre'].value_counts(normalize=True)
Clinton_histo = Sel['Clinton_2chiffre'].value_counts(normalize=True)
Stein_histo = Sel['Stein_2chiffre'].value_counts(normalize=True)

His = pd.DataFrame({'Trump_histo': Trump_histo, 'Clinton_histo': Clinton_histo, 'Stein_histo': Stein_histo})
His = His.rename_axis('Chiffre')
display(His)

# Deuxième méthode
# cols = ['Trump_2chiffre', 'Clinton_2chiffre', 'Stein_2chiffre']
# # His = Sel[cols].apply(pd.Series.value_counts) / nb_bureaux
# His = Sel[cols].apply(lambda x: x.value_counts(normalize=True))
# His = His.rename_axis('Chiffre')
# His = His.rename(columns={"Trump_2chiffre": "Trump_histo", "Clinton_2chiffre": "Clinton_histo", "Stein_2chiffre": "Stein_histo"})
# display(His)
Trump_histo Clinton_histo Stein_histo
Chiffre
0 0.100000 0.086364 0.109091
1 0.140909 0.113636 0.136364
2 0.104545 0.122727 0.063636
3 0.109091 0.090909 0.095455
4 0.113636 0.104545 0.163636
5 0.104545 0.090909 0.027273
6 0.109091 0.122727 0.109091
7 0.095455 0.109091 0.063636
8 0.063636 0.095455 0.104545
9 0.059091 0.063636 0.127273

On ajoute la colonne Benford avec les effectifs théoriques des seconde chiffres attendus par la loi de Benford :

# On ajoute la colonne Benford avec les effectifs théoriques
# His['Benford'] = { Chiffre : round(p(Chiffre)*nb_bureaux) for Chiffre in His.index}
His['Benford'] = { Chiffre : p(Chiffre) for Chiffre in His.index}
His
Trump_histo Clinton_histo Stein_histo Benford
Chiffre
0 0.100000 0.086364 0.109091 0.119679
1 0.140909 0.113636 0.136364 0.113890
2 0.104545 0.122727 0.063636 0.108821
3 0.109091 0.090909 0.095455 0.104330
4 0.113636 0.104545 0.163636 0.100308
5 0.104545 0.090909 0.027273 0.096677
6 0.109091 0.122727 0.109091 0.093375
7 0.095455 0.109091 0.063636 0.090352
8 0.063636 0.095455 0.104545 0.087570
9 0.059091 0.063636 0.127273 0.084997

On affiche la distribution des seconds chiffres par candidat.

# His.plot(figsize=(15,5))
# plt.xticks(range(10));
# His.plot.bar(figsize=(15,5));

plt.figure(figsize=(10,5))
plt.subplot(2,2,1)
sns.barplot(data=His, x=His.index, y='Trump_histo', color='blue', alpha=0.5)
plt.subplot(2,2,2)
sns.barplot(data=His, x=His.index, y='Clinton_histo', color='red', alpha=0.5)
plt.subplot(2,2,3)
sns.barplot(data=His, x=His.index, y='Stein_histo', color='green', alpha=0.5)
plt.subplot(2,2,4)
sns.barplot(data=His, x=His.index, y='Benford', color='black', alpha=0.5)
plt.tight_layout();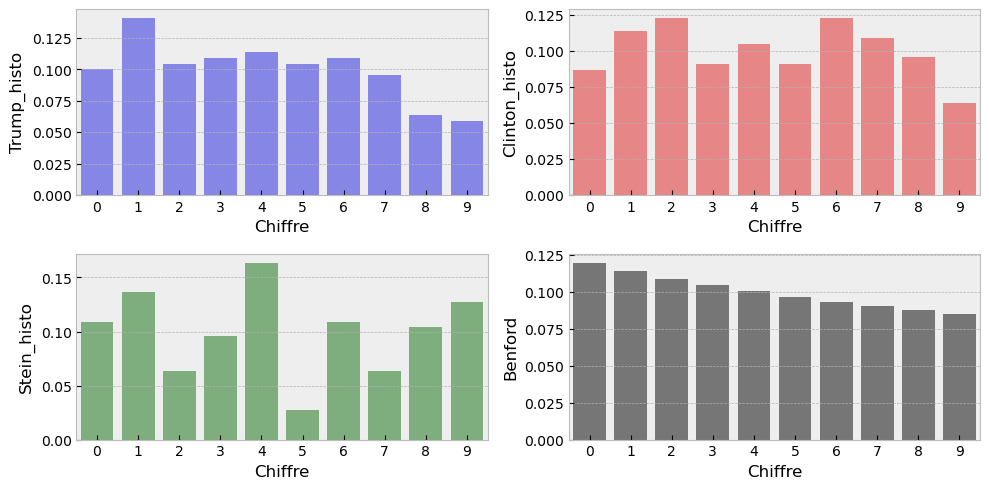

Pour chaque candidat, on calcule la distance euclidienne entre les effectifs théoriques et les effectifs de chaque candidats. Si A et B sont deux listes de même longueur, la distance euclidienne entre A et B est donnée par : \[\text{dist}(A,B) = || A-B ||_2 =\sqrt{\sum_{c=0}^9 \left( A_c - B_c \right)^2}.\] Dans numpy, cela se calcule simplement par np.linalg.norm(A-B).

# Dictionnaire pour stocker les distances
D = {}

# Pour chaque candidat, calculer la norme euclidienne entre les colonnes
for candidat in ["Trump_histo", "Clinton_histo", "Stein_histo"]:
    D[candidat] = np.linalg.norm(His[candidat] - His['Benford'])

D
{'Trump_histo': 0.05398891120857391,
 'Clinton_histo': 0.05714784909840473,
 'Stein_histo': 0.12083530757488783}

Selon ces valeurs, le candidat Stein semble légitime à contester les résultats. Mais est-ce effectivement si rare d’obtenir une telle distance ?

7 Bonus : Simulation pour la détection d’éventuelles anomalies

Pour commencer, on simule 10 votations qui suivent la loi de Benford.

# Créer une copie de Sel et ajouter une colonne avec des chiffres simulés selon FB
Sel_copy = Sel.copy()

for test in ["test"+str(i) for i in range(1,11)]:
    # Générer nb_bureaux chiffres aléatoires selon la distribution FB
    Sel_copy[test] = np.random.choice(range(10), size=nb_bureaux, p=FB)  
    # Calculer les effectifs pour la colonne simulée
    # His[test] = Sel_copy[test].value_counts() 
    His[test] = Sel_copy[test].value_counts(normalize=True) 
    # Calculer la norme entre les effectifs simulés et ceux de Benford
    D[test] = np.linalg.norm(His[test] - His['Benford'])

# Affichage des distances un peu plus joli
pd.DataFrame( index=D.keys(), data=D.values(), columns=['Distance']).sort_values(by='Distance')
Distance
test10 0.038511
test7 0.046972
test5 0.052113
Trump_histo 0.053989
Clinton_histo 0.057148
test3 0.057450
test9 0.064272
test1 0.065174
test8 0.068003
test6 0.076381
test4 0.080832
test2 0.087783
Stein_histo 0.120835

Bien que la valeur semble effectivement élevée pour Stein, il est possible que cette valeur ne soit pas si rares. En effet, dans nos 10 simulations, nous avons parfois obtenu des valeurs de distance euclidienne presque aussi élevées que celles observées pour Stein. Pour comprendre s’il s’agit d’evenement rares, on simule \(10^4\) fois pour voir combien de fois D['test']>D[candidat] :

distance_Stein = D['Stein_histo']
distance_Clinton = D['Clinton_histo']
distance_Trump = D['Trump_histo']


cpt_Stein = 0
cpt_Clinton = 0
cpt_Trump = 0

N = 10_000
for i in range(N):
    test = pd.Series(np.random.choice(range(10), size=nb_bureaux, p=FB)) # le chiffre i apparait avec une probabilité FB[i] et ce pour 220 bureaux de vote
    # test_histo = test.value_counts()
    test_histo = test.value_counts(normalize=True)
    D_test = np.linalg.norm( test_histo - His['Benford'])
    if D_test > distance_Stein:
        cpt_Stein += 1
    if D_test > distance_Clinton:
        cpt_Clinton += 1
    if D_test > distance_Trump:
        cpt_Trump += 1

print(f"""Sur {N} simulations,
 • {cpt_Stein} fois on a obtenu une distance supérieure à celle de Stein, soit {cpt_Stein/N*100:.2f}% des fois;
 • {cpt_Clinton} fois on a obtenu une distance supérieure à celle de Clinton, soit {cpt_Clinton/N*100:.2f}% des fois;
 • {cpt_Trump} fois on a obtenu une distance supérieure à celle de Trump, soit {cpt_Trump/N*100:.2f}% des fois.
  """)
Sur 10000 simulations,
 • 4 fois on a obtenu une distance supérieure à celle de Stein, soit 0.04% des fois;
 • 6184 fois on a obtenu une distance supérieure à celle de Clinton, soit 61.84% des fois;
 • 6972 fois on a obtenu une distance supérieure à celle de Trump, soit 69.72% des fois.

8 Conclusion

La visualisation de la distribution des effectifs du second chiffre des résultats de vote dans les bureaux des états du pour chaque candidat à montré une anomalie. Les résultats ne sont pas conforme à la loi théorique de Benford. De plus, très peu de simulations ont donné des écarts encore plus importants pour le candidat Stein, autrement dit c’est très rare de voir une telle distribution.

Retour au sommet