CM 6 - Schémas à un pas de type 🎨 Runge-Kutta 🎨


Comme nous l’avons vu au CM 5, les barrières sur l’ordre de convergence des méthodes multipas linéaires sont de plus en plus sévères. Nous allons alors étudier une autre famille de méthodes, à savoir les méthodes de Runge-Kutta. La stratégie est nouvelle par rapport à celle des méthodes multipas : en effet, on construit des méthodes à un seul pas, mais nous passons à une stratégie multi-étapes s’appuyant sur l’information en quelques points supplémentaires, situés à l’intérieur de chaque sous-intervalle de la discrétisation du domaine.
1 Schémas
Les schémas de Runge-Kutta sont des méthodes à un pas qui approchent l’intégrale \(\int_{t_n}^{t_{n+1}} \varphi(t,y(t))\mathrm{d}t\) par une formule de quadrature en des points donnés toujours à l’intérieur de l’intervalle \([t_{n};t_{n+1}]\): \(\begin{align*} t_{n,i} & \stackrel{\text{déf}}{=}t_n+c_ih \qquad\text{avec }c_i\in[0;1] \\ \int_{t_n}^{t_{n+1}} \varphi(t,y(t))\mathrm{d}t &\approx h\sum_{i=1}^sb_i \varphi(t_{n,i},y(t_{n,i})). \end{align*}\) Le problème est que, si \(c_i\neq0\) et \(c_i\neq1\), alors \(t_{n,i}\) n’est pas un point de la discrétisation et on ne connait pas \(y(t_{n,i})\). L’évaluation des \(\varphi(t_{n,i},y(t_{n,i}))\) en les points intérieurs est alors approchée par une autre formule de quadrature: \( \varphi(t_{n,i},y(t_{n,i})) \approx \varphi\left(t_{n,i},y_n+h\sum_{j=1}^{s}a_{ij} \varphi(t_{n,j},y(t_{n,j}))\right). \) Cela donne \( y_{n+1} \approx y_n + h \sum_{i=1}^s\left[b_i \varphi\left(t_{n,i},y_n+h\sum_{j=1}^{s}a_{ij} \varphi(t_{n,j},y_{n,j})\right)\right] \)
Une méthode de Runge-Kutta à \(s\ge1\) étages s’écrit: \(\begin{cases} u_0=y(t_0)=y_0,\\ u_{n+1}=u_{n}+h \displaystyle\sum_{i=1}^sb_iK_i& n=0,1,\dots N-1\\ K_i=\displaystyle\varphi\left( t_n+hc_i,u_n+h\sum_{j=1}^{s}a_{ij}K_j \right) & i=1,\dots s. \end{cases}\)
2 Matrice de Butcher
Les coefficients sont généralement organisés en deux vecteurs \(\mathbf{b}=(b_1,\dots,b_s)^T\), \(\mathbf{c}=(c_1,\dots,c_s)^T\) et une matrice \(\mathbb{A}=(a_{ij})_{1\le i,j\le s}\). Le tableau
\(
\begin{array}{c|c}
\mathbf{c} & \mathbb{A}\\
\hline
&\mathbf{b}^T
\end{array}
\)
est appelée matrice de Butcher de la méthode Runge-Kutta considérée.
Si \(a_{ij}=0\) pour \(j\ge i\) (i.e. la matrice \(\mathbb{A}\) est triangulaire inférieure stricte) alors la méthode est explicite car chaque \(K_i\) peut être explicitement calculé en fonction des \(i-1\) coefficients \(K_1,\dots,K_{i-1}\) déjà connus;
Si \(a_{ij}=0\) pour \(j> i\) (i.e. la matrice \(\mathbb{A}\) est triangulaire inférieure) alors la méthode est dite semi-implicite ou diagonalement implicite (diagonal implicit RK, DIRK), i.e. chaque \(K_i\) est solution de l’équation non linéaire
\( \boxed{K_i}=\varphi\left(t_n+c_ih, u_n+ha_{ii}\boxed{K_i}+h\sum_{j=1}^{i-1}a_{ij}K_j\right) \)
Un schéma semi-implicite implique donc la résolution de \(s\) équations non linéaires indépendantes.
Si de plus tous les termes diagonaux sont égaux \(a_{ii}=\gamma\) pour \(i=1,\dots,s\), on parle de singly diagonal implicit method (SDIRK).Dans les autres cas la méthode est implicite et il faut résoudre un système non linéaire de dimension \(s\) pour calculer les \(K_i\).
Bien noter que la méthode est implicite non pas parce que \(u_{n+1}\) dépend de lui même, mais parce qu’au moins un \(K_i\) dépend de lui même!
Notons aussi que, si \(c_s=1\) et \(a_{sj}=b_j\) pour tout \(j=1,\dots,s\) alors \(K_s=\varphi(t_{n+1},u_{n+1})\).
L’augmentation des calculs pour les schémas implicites rend leur utilisation coûteuse; un compromis acceptable sont les méthodes semi-implicites:
3 Ordre de convergence
L’étude de l’ordre des méthodes de Runge-Kutta utilise la théorie de Butcher. Elle repose sur des outils qui combinent l’analyse numérique, la théorie des graphes et la différenciation des champs vectoriels. Plus tard, des relations avec la théorie des groupes et la théorie quantique des champs ont été découvertes. Une monographie de référence sur la théorie de l’ordre de Butcher et les problèmes connexes est rédigée par John C. Butcher lui-même. L’outil de base qui relie tous les domaines susmentionnés est la notion d’arbres racinés. Nous n’énoncerons ici que les résultats.
Soit \(\omega\) l’ordre de la méthode.Proposition (consistance et convergence).
La méthode de Runge-Kutta est consistante (i.e. \(\omega\ge1\)) ssi \(\begin{cases} \displaystyle\sum_{j=1}^s b_{i}=1& \\ \displaystyle c_i=\sum_{j=1}^s a_{ij}&i=1,\dots,s \end{cases}\)
Puisque les méthodes Runge-Kutta sont toutes zéro-stables, les méthodes consistantes sont également convergentes.
Remarque En particulier, pour une méthode explicite on aura \(c_1=a_{1,j}=0\) ainsi \(K_1=\varphi(t_n,u_n)\) et \(c_2=a_{21}\) ainsi \(K_2=\varphi(t_n+c_2h,u_n+hc_2K_1)\).
- Si \(\displaystyle\sum_{j=1}^s b_j c_j=\frac{1}{2}\) alors \(\omega\ge2\)
- Si \(\begin{cases}\displaystyle\sum_{j=1}^s b_j c_j^2=\frac{1}{3}\\\displaystyle\sum_{i=1}^s\sum_{j=1}^s b_i a_{ij} c_j=\frac{1}{6}\end{cases}\) alors \(\omega\ge3\)
- Si \(\begin{cases}\displaystyle\sum_{j=1}^s b_j c_j^3=\frac{1}{4}&\\\displaystyle\sum_{i=1}^s\sum_{j=1}^s b_i c_i a_{ij} c_j=\frac{1}{8}\\\displaystyle\sum_{i=1}^s\sum_{j=1}^s b_i a_{ij} c_j^2=\frac{1}{12}\\\displaystyle\sum_{i=1}^s\sum_{j=1}^s\sum_{k=1}^s b_i a_{ij}a_{jk} c_k=\frac{1}{24}\end{cases}\) alors \(\omega\ge4\)
(Pour les méthodes ERK cf. page 135 de E. Hairer, S. R Norsett, G. Wanner, Solving Ordinary Differential Equations I. Nonstiff Problems, Second Revised Edition, 2008)
Code
def ordre_RK(s, A=None, b=None, c=None):
j = sympy.symbols('j')
if A is None:
A = sympy.MatrixSymbol('a', s, s)
else:
A = sympy.Matrix(A)
if c is None:
c = sympy.symbols(f'c_0:{</span>s<span class="sc">}')
if b is None:
b = sympy.symbols(f'b_0:{</span>s<span class="sc">}')
display(Markdown("**Matrice de Butcher**"))
matrice_Butcher(s, A, b, c)
display(Markdown(f"**On a {</span>s<span class="op">+</span><span class="dv">1</span><span class="sc">} conditions pour avoir consistance = pour être d'ordre 1**"))
ordre_1(s, A, b, c, j)
display(Markdown("**On doit ajouter 1 condition pour être d'ordre 2**"))
ordre_2(s, A, b, c, j)
display(Markdown("**On doit ajouter 2 conditions pour être d'ordre 3**"))
ordre_3(s, A, b, c, j)
display(Markdown("**On doit ajouter 4 conditions pour être d'ordre 4**"))
ordre_4(s, A, b, c, j)
return None
def matrice_Butcher(s, A, b, c):
But = sympy.Matrix(A)
But = But.col_insert(0, sympy.Matrix(c))
last = [sympy.Symbol(" ")]
last.extend(b)
But = But.row_insert(s,sympy.Matrix(last).T)
prlat(sympy.Matrix(But))
return None
def ordre_1(s, A, b, c, j):
texte = "\sum_{j=1}^s b_j =" + f"{</span><span class="bu">sum</span>(b)<span class="sc">.</span>simplify()<span class="sc">}"
texte += r"\text{ doit être égale à }1"
display(Math(texte))
for i in range(s):
somma = sympy.summation(A[i,j],(j,0,s-1)).simplify()
texte = r'\sum_{j=1}^s a_{'</span><span class="op">+</span><span class="bu">str</span>(i)<span class="op">+</span><span class="vs">r'j}=' + sympy.latex( somma )
texte += r"\text{ doit être égale à }"+sympy.latex(c[i])
display(Math( texte ))
return None
def ordre_2(s, A, b, c, j):
texte = '\sum_{j=1}^s b_j c_j=' +sympy.latex(sum([b[i]*c[i] for i in range(s)]).simplify())
texte += r"\text{ doit être égale à }\frac{1}{2}"
display(Math(texte))
return None
def ordre_3(s, A, b, c, j):
texte = '\sum_{j=1}^s b_j c_j^2='
texte += sympy.latex( sum([b[i]*c[i]**2 for i in range(s)]).simplify() )
texte += r"\text{ doit être égale à }\frac{1}{3}"
display(Math(texte))
texte = r'\sum_{i,j=1}^s b_i a_{ij} c_j='
b = sympy.IndexedBase('b')
c = sympy.IndexedBase('c')
j = sympy.symbols('j')
i = sympy.symbols('i')
somma = sympy.summation(b[i]*A[i,j]*c[j],(j,0,s-1),(i,0,s-1) ).simplify()
texte = texte + sympy.latex(somma)
texte += r"\text{ doit être égale à }\frac{1}{6}"
display(Math(texte))
return None
def ordre_4(s, A, b, c, j):
texte = '\sum_{j=1}^s b_j c_j^3='
texte += sympy.latex( sum([b[i]*c[i]**3 for i in range(s)]).simplify() )
texte += r"\text{ doit être égale à }\frac{1}{4}"
display(Math(texte))
texte = r'\sum_{i,j=1}^s b_i c_i a_{ij} c_j='
b = sympy.IndexedBase('b')
c = sympy.IndexedBase('c')
j = sympy.symbols('j')
i = sympy.symbols('i')
somma = sympy.summation(b[i]*c[i]*A[i,j]*c[j],(j,0,s-1),(i,0,s-1) ).simplify()
texte = texte + sympy.latex(somma)
texte += r"\text{ doit être égale à }\frac{1}{8}"
display(Math(texte))
texte = r'\sum_{i,j=1}^s b_i a_{ij} c_j^2='
b = sympy.IndexedBase('b')
c = sympy.IndexedBase('c')
j = sympy.symbols('j')
i = sympy.symbols('i')
somma = sympy.summation(b[i]*A[i,j]*c[j]**2,(j,0,s-1),(i,0,s-1) ).simplify()
texte = texte + sympy.latex(somma)
texte += r"\text{ doit être égale à }\frac{1}{12}"
display(Math(texte))
texte = r'\sum_{i,j,k=1}^s b_i a_{ij} a_{jk} c_k='
b = sympy.IndexedBase('b')
c = sympy.IndexedBase('c')
j = sympy.symbols('j')
i = sympy.symbols('i')
k = sympy.symbols('k')
somma = sympy.summation(b[i]*A[i,j]*A[j,k]*c[k],(k,0,s-1),(j,0,s-1),(i,0,s-1) ).simplify()
texte = texte + sympy.latex(somma)
texte += r"\text{ doit être égale à }\frac{1}{24}"
display(Math(texte))
return None
# exemple
s = 1
display(Markdown(f"### Exemple de méthode de Runge-Kutta à {</span>s<span class="sc">} étages"))
ordre_RK(s)3.1 Exemple de méthode de Runge-Kutta à 1 étages
Matrice de Butcher
\(\displaystyle \left[\begin{matrix}c_{0} & a_{0, 0}\\ & b_{0}\end{matrix}\right]\)
On a 2 conditions pour avoir consistance = pour être d’ordre 1
\(\displaystyle \sum_{j=1}^s b_j =b_0\text{ doit être égale à }1\)
\(\displaystyle \sum_{j=1}^s a_{0j}=a_{0, 0}\text{ doit être égale à }c_{0}\)
On doit ajouter 1 condition pour être d’ordre 2
\(\displaystyle \sum_{j=1}^s b_j c_j=b_{0} c_{0}\text{ doit être égale à }\frac{1}{2}\)
On doit ajouter 2 conditions pour être d’ordre 3
\(\displaystyle \sum_{j=1}^s b_j c_j^2=b_{0} c_{0}^{2}\text{ doit être égale à }\frac{1}{3}\)
\(\displaystyle \sum_{i,j=1}^s b_i a_{ij} c_j={b}_{0} {c}_{0} a_{0, 0}\text{ doit être égale à }\frac{1}{6}\)
On doit ajouter 4 conditions pour être d’ordre 4
\(\displaystyle \sum_{j=1}^s b_j c_j^3=b_{0} c_{0}^{3}\text{ doit être égale à }\frac{1}{4}\)
\(\displaystyle \sum_{i,j=1}^s b_i c_i a_{ij} c_j={b}_{0} {c}_{0}^{2} a_{0, 0}\text{ doit être égale à }\frac{1}{8}\)
\(\displaystyle \sum_{i,j=1}^s b_i a_{ij} c_j^2={b}_{0} {c}_{0}^{2} a_{0, 0}\text{ doit être égale à }\frac{1}{12}\)
\(\displaystyle \sum_{i,j,k=1}^s b_i a_{ij} a_{jk} c_k={b}_{0} {c}_{0} a_{0, 0}^{2}\text{ doit être égale à }\frac{1}{24}\)
3.2 Lien entre l’ordre de convergence \(\omega\) et le nombre d’étages \(s\)
Si une méthode explicite de Runge-Kutta à s-étages est d’ordre \(\omega\), on peut prouver que le nombre d’étages doit satisfaire \(s\ge\omega\), et si \(\omega\ge5\), alors \(s\ge\omega+1\). Cependant, il s’agit d’une condition nécessaire mais on peut prouver qu’elle n’est pas toujours suffisante, autrement dit, dans certains cas, il est prouvé que la limite minimale ne peut pas être atteinte. Par exemple, Butcher a prouvé que pour avoir un ordre \(\omega>6\), il n’existe pas de méthode explicite avec \(s=\omega+1\) étages. Butcher a également prouvé que pour \(\omega>7\), il n’existe pas de méthode explicite de Runge-Kutta avec \(s=\omega+2\) étages. En général, le nombre minimum précis d’étages pour qu’une méthode explicite de Runge-Kutta ait l’ordre \(\omega\) reste un problème ouvert. Certaines valeurs connues sont connues :
\( \begin{array}{c|cccccccc} \omega & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 \\ \hline s \text{ minimal} & 1 & 2 & 3 & 4 & 6 & 7 & 9 & 11\\ \end{array} \)
Les limites ci-dessus ont été démontrées et impliquent alors que nous ne pouvons pas trouver de méthodes d’ordre nécessitant moins d’étages que les méthodes que nous connaissons déjà pour ces ordres. Les travaux de Butcher prouvent également que les méthodes d’ordre \(7\) et \(8\) ont un minimum de \(9\) et \(11\) étages, respectivement.
Autrement dit, un schéma RK explicite à \(s\) étages est au mieux d’ordre \(s\), mais cela seulement si \(s < 5\). Si \(s\ge5\), alors il sera au mieux d’ordre \(s-1\), mais ce n’est même pas garanti.
On peut résumer les résultats de Butcher par le théorème suivant :
Théorème (Barrières de Butcher)
Soit une méthode RK à \(s\) étapes d’ordre \(\omega\).
- Si la méthode est implicite alors \(\color{red}\omega\le 2s\).
- Si la méthode est explicite et \(s<5\) alors \(\color{red}\omega\le s\).
- Si la méthode est explicite et \(s\ge5\) alors \(\color{red}\omega < s\).
Exemples (on verra plus tard les matrices associées à ces méthodes):
- le schéma d’Euler explicite peut s’écrire comme un schéma RK explicite à 1 étage et est d’ordre 1 (\(\omega=s<5\)),
- le schéma d’Euler implicite peut s’écrire comme un schéma RK implicite à 1 étage et est d’ordre 1 (\(\omega\le 2s\)),
- le schéma d’Euler modifié peut s’écrire comme un schéma RK explicite à 2 étages et est d’ordre 2 (\(\omega=s<5\)),
- le schéma de Heun peut s’écrire comme un schéma RK explicite à 2 étages et est d’ordre 2 (\(\omega=s<5\)),
- le schéma de Cranck-Nicholson peut s’écrire comme un schéma RK implicite à 2 étages et est d’ordre 2 (\(\omega\le 2s\)),
Théorème de Kuntzmann et Butcher pour des méthodes d’ordre 2s
Soit les conditions suivantes:
- \(B_p\): \(\sum_i b_i c_i^{q-1}=\frac{1}{q}\) pour \(q=1,\dots,p\)
- \(C_\eta\): \(\sum_j a_{ij} c_j^{q-1}=\frac{c_i^q}{q}\) pour \(i=1,\dots,s\) et \(q=1,\dots,\eta\)
- \(D_\zeta\): \(\sum_i b_i c_i^{q-1}a_{ij} =\frac{b_j}{q}(1-c_j^q)\) pour \(j=1,\dots,s\) et \(q=1,\dots,\zeta\)
Si les coefficients de la méthode de RK vérifient les conditions \(B_p\), \(C_\eta\) et \(D_\zeta\) pour \(p\le\eta + \zeta + 1\) et \(p \le 2\eta + 2\) alors la méthode est d’ordre \(p\).
Cf. E. Hairer, S.P. Norsett, G. Wanner, Solving Ordinary Differential Equations I, page 208
Remarque (le cas des systèmes) Une méthode de Runge-Kutta peut être aisément étendue aux systèmes d’équations différentielles ordinaires. Néanmoins, l’ordre d’une méthode RK dans le cas scalaire ne coı̈ncide pas nécessairement avec celui de la méthode analogue dans le cas vectoriel. En particulier, pour \(p \ge 4\), une méthode d’ordre \(p\) dans le cas du système autonome \(\mathbf{y}'(t)=\boldsymbol{\varphi}(t,\mathbf{y})\), avec \(\boldsymbol{\varphi}\colon \mathbb{R}^m\to\mathbb{R}^n\) est encore d’ordre \(p\) quand on l’applique à l’équation scalaire autonome \(\mathbf{y}'(t)=\boldsymbol{\varphi}(\mathbf{y})\), mais la réciproque n’est pas vraie.
4 A-stabilité
Rappelons la définition de schéma A-stable:
Soit \(\lambda\in\mathbb{C}\) avec \(\Re(\lambda)=-\beta\) où \(\beta\) est un nombre réel positif et considérons le problème de Cauchy \(\begin{cases} y'(t)=\lambda y(t), &\text{pour }t>0,\\ y(0)=y_0 \end{cases}\) où \(y_0\neq0\) est une valeur donnée. Sa solution est \(y(t)=y_0e^{\lambda t}\) donc \(\lim_{t\to+\infty}|y(t)|=0.\) Soit \(h>0\) un pas de temps donné, \(t_n=nh\) pour \(n\in\mathbb{N}\) et notons \(u_n\approx y(t_n)\) une approximation de la solution \(y\) au temps \(t_n\). Si, sous d’éventuelles conditions sur \(h\), on a \( \lim_{n\to+\infty} u_n =0, \) alors on dit que le schéma est A-stable.
Dans le cas \(\lambda\in\mathbb{R}^-\), i.e. \(-\lambda=\beta>0\), une méthode de Runge-Kutta à \(s\ge1\) étages pour \(y'(t)=-\beta y(t)\) s’écrit: \(\begin{cases} u_0=y_0,\\ u_{n+1}=u_{n}+h \displaystyle\sum_{i=1}^sb_iK_i& n=0,1,\dots N-1\\ K_i=\displaystyle -\beta \left( u_n+h\sum_{j=1}^{s}a_{ij}K_j \right) & i=1,\dots s. \end{cases}\)
On peut vérifier que, contrairement aux méthodes multi-pas, la taille des régions de stabilité absolue des méthodes RK augmente quand l’ordre augmente.
Régions de stabilité absolue pour certaines méthodes RK explicites.
Source: A. Quarteroni, F. Saleri, P. Gervasio Calcul Scientifique: Cours, exercices corrigés et illustrations en Matlab et Octave.

5 Exercice : schémas RK à un étage
Étudier les méthodes RK avec \(s=1\) consistants :
- écrire le schéma implicite générique RK à un étage
- étudier son ordre de convergence
- écrire le schéma explicite générique RK à un étage
- étudier son ordre de convergence
- étudier la A-stabilité
5.1 Correction : écriture d’un schéma RK à un étage quelconque
Ces méthodes ont pour matrice de Butcher \( \begin{array}{c|cc} c_1 & a_{11}\\ \hline & b_1 \end{array} \text{ avec } \begin{cases} c_1=a_{11}\\ b_1=1 \end{cases} \quad \implies \begin{array}{c|cc} c_1 & c_1\\ \hline & 1 \end{array} \quad \implies \begin{cases} u_0 = y_0 \\ K_1 = \varphi\left(t_n+hc_1,u_n+h c_{1}K_1\right)\\ u_{n+1} = u_n + h K_1 & n=0,1,\dots N-1 \end{cases} \)
Par exemple, si on choisit \(c_1=1\) on trouve le schéma implicite
\( \begin{array}{c|cc} 1 & 1\\ \hline & 1 \end{array} \quad \implies \begin{cases} u_0 = y_0 \\ K_1 = \varphi\left(t_{n+1},u_n+h K_1\right)\\ u_{n+1} = u_n + h K_1 & n=0,1,\dots N-1 \end{cases} \)
Notons que ce schéma n’est rien d’autre que le schéma d’Euler implicite car \(u_{n+1} = u_n+h K_1\), donc si on remplace le \(u_n+h K_1\) dans la définition de \(K_1\) par \(u_{n+1}\) on obtient
\(
K_1
= \varphi\left(t_{n+1},u_n+h K_1\right)
= \varphi\left(t_{n+1},u_{n+1}\right)
\quad\implies\quad
u_{n+1} = u_n + h K_1=u_n + h \varphi\left(t_{n+1},u_{n+1}\right)
\)
En effet, \(c_s=1\) et \(a_{sj}=b_j\) pour tout \(j=1,\dots,s\) alors \(K_s=\varphi(t_{n+1},u_{n+1})\).
5.2 Correction : étude de l’ordre d’un schéma RK à un étage quelconque
Si on cherche une méthode d’ordre \(2\) alors il faut que \(1\times c_1=\frac{1}{2}\): il existe une seule méthode d’ordre 2, elle est implicite et sa matrice de Butcher est
\( \begin{array}{c|cc} \frac{1}{2} & \frac{1}{2}\\ \hline & 1 \end{array} \quad \implies \begin{cases} u_0 = y_0 \\ K_1 = \varphi\left(t_n+\frac{h}{2},u_n+\frac{h}{2}K_1\right)\\ u_{n+1} = u_n + h K_1 & n=0,1,\dots N-1 \end{cases} \)
Notons que \(u_{n+1} = u_n+h K_1\), donc si on remplace le \(u_n+\frac{h}{2} K_1=\frac{u_n+\left(u_n+h K_1\right)}{2}\) dans la définition de \(K_1\) par \(u_{n+1}\) on obtient le schéma RK1_M
\(
K_1
= \varphi\left(t_{n}+\frac{h}{2},u_n+\frac{h}{2} K_1\right)
= \varphi\left(t_{n}+\frac{h}{2},\frac{u_n+u_{n+1}}{2}\right)
\quad\implies\quad
u_{n+1} = u_n + h K_1=u_n + h \varphi\left(\frac{t_n+t_{n+1}}{2},\frac{u_n+u_{n+1}}{2}\right)
\)
Matrice de Butcher
\(\displaystyle \left[\begin{matrix}c_{0} & a_{0, 0}\\ & b_{0}\end{matrix}\right]\)
On a 2 conditions pour avoir consistance = pour être d’ordre 1
\(\displaystyle \sum_{j=1}^s b_j =b_0\text{ doit être égale à }1\)
\(\displaystyle \sum_{j=1}^s a_{0j}=a_{0, 0}\text{ doit être égale à }c_{0}\)
On doit ajouter 1 condition pour être d’ordre 2
\(\displaystyle \sum_{j=1}^s b_j c_j=b_{0} c_{0}\text{ doit être égale à }\frac{1}{2}\)
On doit ajouter 2 conditions pour être d’ordre 3
\(\displaystyle \sum_{j=1}^s b_j c_j^2=b_{0} c_{0}^{2}\text{ doit être égale à }\frac{1}{3}\)
\(\displaystyle \sum_{i,j=1}^s b_i a_{ij} c_j={b}_{0} {c}_{0} a_{0, 0}\text{ doit être égale à }\frac{1}{6}\)
On doit ajouter 4 conditions pour être d’ordre 4
\(\displaystyle \sum_{j=1}^s b_j c_j^3=b_{0} c_{0}^{3}\text{ doit être égale à }\frac{1}{4}\)
\(\displaystyle \sum_{i,j=1}^s b_i c_i a_{ij} c_j={b}_{0} {c}_{0}^{2} a_{0, 0}\text{ doit être égale à }\frac{1}{8}\)
\(\displaystyle \sum_{i,j=1}^s b_i a_{ij} c_j^2={b}_{0} {c}_{0}^{2} a_{0, 0}\text{ doit être égale à }\frac{1}{12}\)
\(\displaystyle \sum_{i,j,k=1}^s b_i a_{ij} a_{jk} c_k={b}_{0} {c}_{0} a_{0, 0}^{2}\text{ doit être égale à }\frac{1}{24}\)
5.3 Correction : écriture d’un schéma RK à un étage explicite
Si le schéma est explicite alors
\( \begin{array}{c|cc} 0 & 0\\ \hline & 1 \end{array} \quad \implies \begin{cases} u_0 = y_0 \\ K_1 = \varphi\left(t_n,u_n\right)\\ u_{n+1} = u_n + h K_1 & n=0,1,\dots N-1 \end{cases} \)
Il existe un seul schéma explicite RK à un étage, il s’agit du schéma d’Euler explicite.
5.4 Correction : étude de l’ordre d’un schéma RK à un étage explicite
Si le schéma est explicite alors il est d’ordre 1.
5.5 Correction : étude de la A-stabilité
Une méthode de Runge-Kutta à 1 étage pour \(y'(t)=-\beta y(t)\) s’écrit :
\(\begin{cases}
u_0=y_0,\\
u_{n+1}=u_{n}+h K_1& n=0,1,\dots N-1\\
K_1=-\beta \left( u_n+hc_1K_1 \right).
\end{cases}\)
On trouve donc \((1+\beta hc_1)K_1=-\beta u_n\) ainsi
\(\begin{cases}
u_0 = y_0 \\
u_{n+1} = \left(1-\frac{(\beta h)}{1+c_1(\beta h)}\right)u_n & n=0,1,\dots N-1
\end{cases}\)
Par induction on obtient
\(
u_{n}=\left(1-\frac{\beta h}{1+c_1\beta h}\right)^nu_0.
\)
Par conséquent, \(\lim\limits_{n\to+\infty}u_n=0\) si et seulement si
\(
\left|1-\frac{\beta h}{1+c_1\beta h}\right|<1.
\)
Notons \(x\) le produit \(\beta h>0\) (donc \(x>0\)) et \(q\) la fonction \(q(x)=1-\frac{x}{1+c_1x}\) (avec \(c_1\in[0;1]\)).
\(\begin{align*}
|q(x)|<1
&\quad\iff\quad
-1<1-\frac{x}{1+c_1x}<1
\quad\iff\quad
\begin{cases}
\frac{x}{1+c_1x}<2\\
\frac{x}{1+c_1x}>0
\end{cases}
\\
&\quad\stackrel{\substack{x>0\\c_1\ge0}}{\iff}\quad
\frac{x}{1+c_1x}<2
\quad\stackrel{c_1x\ge0}{\iff}\quad
x<2(1+c_1x)
\\
&\quad\iff\quad
(1-2c_1)x<2
\quad\iff\quad
\begin{cases}
x<\frac{2}{1-2c_1}&\text{si }1-2c_1>0\\
\forall x&\text{sinon.}
\end{cases}
\end{align*}\) Conclusion:
- si \(c_1\ge \frac{1}{2}\) le schéma est inconditionnellement A-stable,
- si \(c_1<\frac{1}{2}\) le schéma est A-stable ssi \(\beta h <\frac{2}{1-2c_1}\).
Pour nos exemples, on obtient:
- si \(c_1=1\) (Euler Implicite) alors le schéma est inconditionnellement A-stable et d’ordre 1,
- si \(c_1=\frac{1}{2}\) alors le schéma est inconditionnellement A-stable et d’ordre 2,
- si \(c_1=0\) (Euler Explicite) alors le schéma est A-stable ssi \(h<\frac{2}{\beta}\) et il est d’ordre 1.
6 Exercice : schémas RK à deux étages
Étudier les méthodes RK avec \(s=2\) consistantes:
- écrire le schéma implicite générique RK à deux étages
- écrire le schéma semi-implicite générique RK à deux étages
- écrire le schéma explicite générique RK à deux étages
- étudier l’ordre de convergences des schémas explicites
- étudier la A-stabilité des schémas explicites
6.1 Correction : écriture d’un schéma RK à deux étages quelconque
Les méthodes avec \(s=2\) ont pour matrice de Butcher
\( \begin{array}{c|cc} c_1 & a_{11} & a_{12}\\ c_2 & a_{21} & a_{22}\\ \hline & b_1 & b_2 \end{array} \text{ avec } \begin{cases} c_1=a_{11}+a_{12}\\ c_2=a_{21}+a_{22}\\ b_1+b_2=1 \end{cases} \quad \implies \begin{array}{c|cc} c_1 & a_{11} & c_1-a_{11}\\ c_2 & a_{21} & c_2-a_{21}\\ \hline & 1-b_2 & b_2 \end{array} \quad \implies \begin{cases} u_0 = y_0 \\ K_1 = \varphi\left(t_n+hc_1,u_n+h(a_{11}K_1+ (c_1-a_{11})K_2)\right)\\ K_2 = \varphi\left(t_n+hc_2,u_n+h(a_{21}K_1+ (c_2-a_{21})K_2)\right)\\ u_{n+1} = u_n + h\left((1-b_2)K_1+b_2K_2\right) & n=0,1,\dots N-1 \end{cases} \)
Code
def RK(tt,phi,y0):
h = tt[1]-tt[0]
uu = np.zeros_like(tt)
uu[0] = y0
for i in range(len(tt)-1):
# X = [K1,K2]
sys = lambda X : [ -X[0]+phi( tt[i]+h*c1 , uu[i]+h*(a11*X[0]+a12*X[1]) ) ,
-X[1]+phi( tt[i]+h*c2 , uu[i]+h*(a21*X[0]+a22*X[1]) )
]
K_start = phi(tt[i],uu[i])
K1, K2 = fsolve( sys , [K_start,K_start ] )
uu[i+1] = uu[i]+h*(b1*K1+b2*K2)
return uuVoici un exemple, appelé méthode de Gauss: \( \begin{array}{c|cc} \frac{1}{2}-\gamma & \frac{1}{4} & \frac{1}{4}-\gamma\\ \frac{1}{2}+\gamma & \frac{1}{4}+\gamma & \frac{1}{4}\\ \hline & \frac{1}{2} & \frac{1}{2} \end{array} \qquad\text{avec }\gamma=\frac{\sqrt{3}}{6} \)
Cette méthode est d’ordre 4 et on peut monter que c’est la seule méthode d’ordre 4 à deux étages.
Code
Matrice de Butcher
\(\displaystyle \left[\begin{matrix}\frac{1}{2} - \frac{\sqrt{3}}{6} & \frac{1}{4} & \frac{1}{4} - \frac{\sqrt{3}}{6}\\\frac{\sqrt{3}}{6} + \frac{1}{2} & \frac{1}{4} + \frac{\sqrt{3}}{6} & \frac{1}{4}\\ & \frac{1}{2} & \frac{1}{2}\end{matrix}\right]\)
On a 3 conditions pour avoir consistance = pour être d’ordre 1
\(\displaystyle \sum_{j=1}^s b_j =1\text{ doit être égale à }1\)
\(\displaystyle \sum_{j=1}^s a_{0j}=\frac{1}{2} - \frac{\sqrt{3}}{6}\text{ doit être égale à }\frac{1}{2} - \frac{\sqrt{3}}{6}\)
\(\displaystyle \sum_{j=1}^s a_{1j}=\frac{\sqrt{3}}{6} + \frac{1}{2}\text{ doit être égale à }\frac{\sqrt{3}}{6} + \frac{1}{2}\)
On doit ajouter 1 condition pour être d’ordre 2
\(\displaystyle \sum_{j=1}^s b_j c_j=\frac{1}{2}\text{ doit être égale à }\frac{1}{2}\)
On doit ajouter 2 conditions pour être d’ordre 3
\(\displaystyle \sum_{j=1}^s b_j c_j^2=\frac{1}{3}\text{ doit être égale à }\frac{1}{3}\)
\(\displaystyle \sum_{i,j=1}^s b_i a_{ij} c_j=\frac{\left(\left(3 + 2 \sqrt{3}\right) {c}_{0} + 3 {c}_{1}\right) {b}_{1}}{12} + \frac{\left(3 {c}_{0} + \left(3 - 2 \sqrt{3}\right) {c}_{1}\right) {b}_{0}}{12}\text{ doit être égale à }\frac{1}{6}\)
On doit ajouter 4 conditions pour être d’ordre 4
\(\displaystyle \sum_{j=1}^s b_j c_j^3=\frac{1}{4}\text{ doit être égale à }\frac{1}{4}\)
\(\displaystyle \sum_{i,j=1}^s b_i c_i a_{ij} c_j=\frac{\left(\left(3 + 2 \sqrt{3}\right) {c}_{0} + 3 {c}_{1}\right) {b}_{1} {c}_{1}}{12} + \frac{\left(3 {c}_{0} + \left(3 - 2 \sqrt{3}\right) {c}_{1}\right) {b}_{0} {c}_{0}}{12}\text{ doit être égale à }\frac{1}{8}\)
\(\displaystyle \sum_{i,j=1}^s b_i a_{ij} c_j^2=\frac{\left(\left(3 + 2 \sqrt{3}\right) {c}_{0}^{2} + 3 {c}_{1}^{2}\right) {b}_{1}}{12} + \frac{\left(3 {c}_{0}^{2} + \left(3 - 2 \sqrt{3}\right) {c}_{1}^{2}\right) {b}_{0}}{12}\text{ doit être égale à }\frac{1}{12}\)
\(\displaystyle \sum_{i,j,k=1}^s b_i a_{ij} a_{jk} c_k=\frac{{b}_{0} {c}_{0}}{24} - \frac{\sqrt{3} {b}_{0} {c}_{1}}{12} + \frac{{b}_{0} {c}_{1}}{8} + \frac{{b}_{1} {c}_{0}}{8} + \frac{\sqrt{3} {b}_{1} {c}_{0}}{12} + \frac{{b}_{1} {c}_{1}}{24}\text{ doit être égale à }\frac{1}{24}\)
Code
# gamma = sympy.sqrt(3)/6
# c = [ sympy.Rational(1,2)-gamma, sympy.Rational(1,2)+gamma ]
# b = [ sympy.Rational(1,2), sympy.Rational(1,2) ]
# A = [ [sympy.Rational(1,4), sympy.Rational(1,4)-gamma],
# [sympy.Rational(1,4)+gamma, sympy.Rational(1,4)]
# ]
s = len(c)
print("🌟 Consistance")
print(sum(b)==1)
for i in range(s):
print(sum(A[i]).simplify()==c[i])
print("\n🌟 Pour être d'ordre 2 il faut que la condition suivante soit vraie:")
print(sum([b[i]*c[i] for i in range(s)]).simplify()==sympy.Rational(1,2))
print("\n🌟 Pour être d'ordre 3 il faut que les conditions suivantes soient vraies:")
print(sum([b[i]*c[i]**2 for i in range(s)]).simplify()==sympy.Rational(1,3))
print(sum([b[i]*A[i][j]*c[j] for i in range(s) for j in range(s)]).simplify()==sympy.Rational(1,6))
print("\n🌟 Pour être d'ordre 4 il faut que les conditions suivantes soient vraies:")
print(sum([b[i]*c[i]**3 for i in range(s)]).simplify()==sympy.Rational(1,4))
print(sum([b[i]*c[i]*A[i][j]*c[j] for i in range(s) for j in range(s)]).simplify()==sympy.Rational(1,8))
print(sum([b[i]*A[i][j]*c[j]**2 for i in range(s) for j in range(s)]).simplify()==sympy.Rational(1,12))
print(sum([b[i]*A[i][j]*A[j][k]*c[k] for i in range(s) for j in range(s) for k in range(s)]).simplify()==sympy.Rational(1,24))🌟 Consistance
True
True
True
🌟 Pour être d'ordre 2 il faut que la condition suivante soit vraie:
True
🌟 Pour être d'ordre 3 il faut que les conditions suivantes soient vraies:
True
True
🌟 Pour être d'ordre 4 il faut que les conditions suivantes soient vraies:
True
True
True
True6.2 Correction : écriture d’un schéma RK à deux étages semi-implicite
Les méthodes semi-implicites vérifient, de plus, \(c_1=a_{11}\) ainsi la matrice de Butcher est \( \begin{array}{c|cc} c_1 & c_1 & 0\\ c_2 & a_{21} & c_2-a_{21}\\ \hline & 1-b_2 & b_2 \end{array} \quad \implies \begin{cases} u_0 = y_0 \\ K_1 = \varphi\left(t_n+hc_1,u_n+hc_{1}K_1\right)\\ K_2 = \varphi\left(t_n+hc_2,u_n+h(a_{21}K_1+ (c_2-a_{21})K_2)\right)\\ u_{n+1} = u_n + h\left((1-b_2)K_1+b_2K_2\right) & n=0,1,\dots N-1 \end{cases} \)
Code
def RK(tt,phi,y0):
h = tt[1]-tt[0]
uu = np.zeros_like(tt)
uu[0] = y0
for i in range(len(tt)-1):
# X = [K1,K2]
K_start = phi(tt[i],uu[i])
K1 = fsolve( lambda x : -x+phi( tt[i]+h*c1 , uu[i]+h*(a11*x) ) , K_start ) [0]
K2 = fsolve( lambda x : -x+phi( tt[i]+h*c2 , uu[i]+h*(a21*K1+a22*x) ) , K_start ) [0]
uu[i+1] = uu[i]+h*(b1*K1+b2*K2)
return uuPar exemple, si on choisit \(c_1=0\), \(c_2=1\) et \(a_{21}=a_{22}=b_1=b_2=\frac{1}{2}\) on trouve le schéma semi-implicite \( \begin{array}{c|cc} 0 & 0 & 0\\ 1 & \frac{1}{2} & \frac{1}{2}\\ \hline & \frac{1}{2} & \frac{1}{2} \end{array} \quad \implies \begin{cases} u_0 = y_0 \\ K_1 = \varphi\left(t_{n},u_n\right)\\ K_2 = \varphi\left(t_{n+1},u_n+\frac{h}{2}(K_1+K_2)\right)\\ u_{n+1} = u_n + \frac{h}{2}(K_1+K_2) & n=0,1,\dots N-1 \end{cases} \)
Notons que ce schéma n’est rien d’autre que le schéma de Crank-Nicolson car \(u_{n+1} = u_n+\frac{h}{2}(K_1+K_2)\), donc si on remplace le \(u_n+\frac{h}{2}(K_1+K_2)\) dans la définition de \(K_2\) par \(u_{n+1}\) on obtient \( K_2 = \varphi\left(t_{n+1},u_n+\frac{h}{2}(K_1+K_2)\right) = \varphi\left(t_{n+1},u_{n+1}\right) \) ainsi \( u_{n+1} = u_n+\frac{h}{2}(K_1+K_2)=u_n + \frac{h}{2}(\varphi\left(t_{n},u_n\right)+\varphi\left(t_{n+1},u_{n+1}\right)) \) En effet, \(c_s=1\) et \(a_{sj}=b_j\) pour tout \(j=1,\dots,s\) alors \(K_s=\varphi(t_{n+1},u_{n+1})\).
Il s’agit donc d’un schéma d’ordre 2.
Code
c = [0, 1]
b = [sympy.Rational(1,2), sympy.Rational(1,2)]
A = [[0, 0], [sympy.Rational(1,2), sympy.Rational(1,2)]]
s = len(c)
print("🌟 Consistance")
print(sum(b)==1)
for i in range(s):
print(sum(A[i])==c[i])
print("\n🌟 Pour être d'ordre 2 il faut que la condition suivante soit vraie:")
print(sum([b[i]*c[i] for i in range(s)]).simplify()==sympy.Rational(1,2))
print("\n🌟 Pour être d'ordre 3 il faut que les conditions suivantes soient vraies:")
print(sum([b[i]*c[i]**2 for i in range(s)]).simplify()==sympy.Rational(1,3))
print(sum([b[i]*A[i][j]*c[j] for i in range(s) for j in range(s)]).simplify()==sympy.Rational(1,6))🌟 Consistance
True
True
True
🌟 Pour être d'ordre 2 il faut que la condition suivante soit vraie:
True
🌟 Pour être d'ordre 3 il faut que les conditions suivantes soient vraies:
False
FalseUn autre exemple est la méthode dite DIRK (Diagonally Implicit Runge-Kutta) qui est d’ordre 3: \( \begin{array}{c|cc} \frac{1}{3} & \frac{1}{3} & 0\\ 1 & 1 & 0\\ \hline & \frac{3}{4} & \frac{1}{4} \end{array} \quad \implies \begin{cases} u_0 = y_0 \\ K_1 = \varphi\left(t_{n}+\frac{1}{3}h,u_n+\frac{1}{3}hK_1\right)\\ K_2 = \varphi\left(t_{n+1},u_n+hK_1\right)\\ u_{n+1} = u_n + \frac{h}{4}(3K_1+K_2) & n=0,1,\dots N-1 \end{cases} \)
Code
c = [sympy.Rational(1,3), 1]
b = [sympy.Rational(3,4), sympy.Rational(1,4)]
A = [[sympy.Rational(1,3),0],[1,0]]
s = len(c)
print("🌟 Consistance")
print(sum(b)==1)
for i in range(s):
print(sum(A[i])==c[i])
print("\n🌟 Pour être d'ordre 2 il faut que la condition suivante soit vraie:")
print(sum([b[i]*c[i] for i in range(s)]).simplify()==sympy.Rational(1,2))
print("\n🌟 Pour être d'ordre 3 il faut que les conditions suivantes soient vraies:")
print(sum([b[i]*c[i]**2 for i in range(s)]).simplify()==sympy.Rational(1,3))
print(sum([b[i]*A[i][j]*c[j] for i in range(s) for j in range(s)]).simplify()==sympy.Rational(1,6))
print("\n🌟 Pour être d'ordre 4 il faut que les conditions suivantes soient vraies:")
print(sum([b[i]*c[i]**3 for i in range(s)]).simplify()==sympy.Rational(1,4))
print(sum([b[i]*c[i]*A[i][j]*c[j] for i in range(s) for j in range(s)]).simplify()==sympy.Rational(1,8))
print(sum([b[i]*A[i][j]*c[j]**2 for i in range(s) for j in range(s)]).simplify()==sympy.Rational(1,12))
print(sum([b[i]*A[i][j]*A[j][k]*c[k] for i in range(s) for j in range(s) for k in range(s)]).simplify()==sympy.Rational(1,24))🌟 Consistance
True
True
True
🌟 Pour être d'ordre 2 il faut que la condition suivante soit vraie:
True
🌟 Pour être d'ordre 3 il faut que les conditions suivantes soient vraies:
True
True
🌟 Pour être d'ordre 4 il faut que les conditions suivantes soient vraies:
False
False
False
False6.3 Correction : écriture d’un schéma RK à deux étages explicite
Les méthodes avec \(s=2\) explicites ont pour matrice de Butcher \( \begin{array}{c|cc} 0 & 0 & 0\\ c_2 & c_{2} & 0\\ \hline & 1-b_2 & b_2 \end{array} \quad \implies \begin{cases} u_0 = y_0 \\ K_1 = \varphi\left(t_n,u_n\right)\\ K_2 = \varphi\left(t_n+hc_2,u_n+hc_2K_1\right)\\ u_{n+1} = u_n + h\left((1-b_2)K_1+b_2K_2\right) & n=0,1,\dots N-1 \end{cases} \)
6.4 Correction : étude de l’ordre d’un schéma RK à deux étages explicite
- Un schéma RK à deux étage explicite est au mieux d’ordre 2.
- Pour avoir l’ordre 2 il faut que \(b_2c_2=\frac{1}{2}\).
Conclusion: un schéma RK à deux étages explicite d’ordre 2 s’écrit \( \begin{array}{c|cc} 0 & 0 & 0\\ \frac{1}{2\alpha} & \frac{1}{2\alpha} & 0\\ \hline & 1-\alpha & \alpha \end{array} \quad \implies \begin{cases} u_0 = y_0 \\ K_1 = \varphi\left(t_n,u_n\right)\\ K_2 = \varphi\left(t_n+\frac{h}{2}\alpha,u_n+\frac{h}{2}\alpha K_1\right)\\ u_{n+1} = u_n + h\left((1-\alpha)K_1+\alpha K_2\right) & n=0,1,\dots N-1 \end{cases} \)
Voici quelques cas particuliers :
\(\alpha=\frac{1}{2}\): schéma de Heun \( \begin{array}{c|cc} 0 & 0 & 0\\ 1 & 1 & 0\\ \hline & \frac{1}{2} & \frac{1}{2} \end{array} \quad \implies \begin{cases} u_0 = y_0 \\ K_1 = \varphi(t_n,u_n)\\ K_2 = \varphi(t_{n+1},u_{n}+hK_1)\\ u_{n+1} = u_n + h\left(\frac{1}{2}K_1+\frac{1}{2}K_2\right) & n=0,1,\dots N-1 \end{cases} \)
\(\alpha=1\): schéma d’Euler Modifié (ou du point milieu) \( \begin{array}{c|cc} 0 & 0 & 0\\ \frac{1}{2} & \frac{1}{2} & 0\\ \hline & 0 & 1 \end{array} \quad \implies \begin{cases} u_0 = y_0 \\ K_1 = \varphi(t_n,u_n)\\ K_2 = \varphi(t_{n}+\frac{1}{2}h,u_{n}+\frac{1}{2}hK_1)\\ u_{n+1} = u_n + h K_2 & n=0,1,\dots N-1 \end{cases} \)
\(\alpha=\frac{2}{3}\): schéma de Ralston \( \begin{array}{c|cc} 0 & 0 & 0\\ \frac{3}{4} & \frac{3}{4} & 0\\ \hline & \frac{1}{3} & \frac{2}{3} \end{array} \quad \implies \begin{cases} u_0 = y_0 \\ K_1 = \varphi(t_n,u_n)\\ K_2 = \varphi(t_{n}+\frac{3}{4}h,u_{n}+\frac{3}{4}hK_1)\\ u_{n+1} = u_n + \frac{h}{3} (K_1+2K_2) & n=0,1,\dots N-1 \end{cases} \)
6.5 Correction : étude de la A-stabilité des schémas explicites
Le schéma donné appliqué à cette équation devient \(\begin{cases} u_0 = y_0 \\ u_{n+1} = \left(1-(\beta h)+c_2b_2(\beta h)^2\right)u_n & n=0,1,\dots N-1 \end{cases}\) Par induction on obtient \( u_{n}=\left(1-(\beta h)+c_2b_2(\beta h)^2\right)^nu_0. \) Par conséquent, \(\lim\limits_{n\to+\infty}u_n=0\) si et seulement si \( \left|1-(\beta h)+c_2b_2(\beta h)^2\right|<1. \) Notons \(x\) le produit \(\beta h>0\) (donc \(x>0\)) et \(q\) le polynôme \(q(x)=1-x+c_2b_2x^2\).
Si \(c_2b_2=0\), le schéma se réduit au schéma d’Euler explicite.
Si \(c_2b_2>0\), c’est une parabole convexe et le sommet est situé en \(\left(\frac{1}{2c_2b_2}>0,1-\frac{1}{4c_2b_2}\right)\). \( |q(x)|<1 \quad\iff\quad x<\frac{1}{c_2b_2} \) En particulier, lorsque le schéma est d’ordre 2 on a \(b_2c_2=\frac{1}{2}\) et le schéma est A-stable ssi \(h<\frac{2}{\beta}\).
Si \(c_2b_2<0\), c’est une parabole concave et le sommet est situé en \(\left(\frac{1}{2c_2b_2}<0,1-\frac{1}{4c_2b_2}\right)\). \( |q(x)|<1 \quad\iff\quad x<\frac{1-\sqrt{1-8b_2c_2}}{2b_2c_2} \)
7 Exemples à 3 étages explicites
Un schéma RK à \(3\) étages explicite a pour matrice de Butcher \( \begin{array}{c|ccc} 0 & 0 & 0 & 0 \\ c_2 & a_{21} & 0&0\\ c_3 & a_{31} &a_{32}&0\\ \hline & b_1 & b_2 & b_3 \end{array} \text{ avec } \begin{cases} c_2=a_{21}\\ c_3=a_{31}+a_{32}\\ b_1+b_2+b_3=1 \end{cases} \quad \implies \begin{cases} u_0 = y_0 \\ K_1 = \varphi\left(t_n,u_n\right)\\ K_2 = \varphi\left(t_n+hc_2,u_n+hc_2K_1\right)\\ K_3 = \varphi\left(t_n+hc_3,u_n+h(a_{31}K_1+ a_{32}K_2)\right)\\ u_{n+1} = u_n + h\left(b_1K_1+b_2K_2+b_3K_3\right) & n=0,1,\dots N-1 \end{cases} \)
Voici trois exemples:
- schéma de Heun à trois étages \( \begin{array}{c|ccc} 0 & 0 & 0 & 0 \\ \frac{1}{3} & \frac{1}{3} & 0&0\\ \frac{2}{3} & 0 &\frac{2}{3}&0\\ \hline & \frac{1}{4} & 0 & \frac{3}{4} \end{array} \quad \implies \begin{cases} u_0 = y_0 \\ K_1 = \varphi\left(t_n,u_n\right)\\ K_2 = \varphi\left(t_n+\frac{h}{3},u_n+\frac{h}{3}K_1\right)\\ K_3 = \varphi\left(t_n+\frac{2}{3}h,u_n+\frac{2}{3}hK_2\right)\\ u_{n+1} = u_n + \frac{h}{4}\left(K_1+3K_3\right) & n=0,1,\dots N-1 \end{cases} \)
Étant une méthode explicite à 3 étapes, elle est au mieux d’ordre 3. Vérifions qu’elle est effectivement d’ordre 3:
Code
c = [0, sympy.Rational(1,3), sympy.Rational(2,3)]
b = [sympy.Rational(1,4), 0, sympy.Rational(3,4)]
A = [[0, 0, 0],
[sympy.Rational(1,3), 0, 0],
[0, sympy.Rational(2,3), 0]]
s = len(c)
print("🌟 Consistance")
print(sum(b)==1)
for i in range(s):
print(sum(A[i])==c[i])
print("\n🌟 Pour être d'ordre 2 il faut que la condition suivante soit vraie:")
print(sum([b[i]*c[i] for i in range(s)]).simplify()==sympy.Rational(1,2))
print("\n🌟 Pour être d'ordre 3 il faut que les conditions suivantes soient vraies:")
print(sum([b[i]*c[i]**2 for i in range(s)]).simplify()==sympy.Rational(1,3))
print(sum([b[i]*A[i][j]*c[j] for i in range(s) for j in range(s)]).simplify()==sympy.Rational(1,6))
print("\n🌟 Pour être d'ordre 4 il faut que les conditions suivantes soient vraies:")
print(sum([b[i]*c[i]**3 for i in range(s)]).simplify()==sympy.Rational(1,4))
print(sum([b[i]*c[i]*A[i][j]*c[j] for i in range(s) for j in range(s)]).simplify()==sympy.Rational(1,8))
print(sum([b[i]*A[i][j]*c[j]**2 for i in range(s) for j in range(s)]).simplify()==sympy.Rational(1,12))
print(sum([b[i]*A[i][j]*A[j][k]*c[k] for i in range(s) for j in range(s) for k in range(s)]).simplify()==sympy.Rational(1,24))🌟 Consistance
True
True
True
True
🌟 Pour être d'ordre 2 il faut que la condition suivante soit vraie:
True
🌟 Pour être d'ordre 3 il faut que les conditions suivantes soient vraies:
True
True
🌟 Pour être d'ordre 4 il faut que les conditions suivantes soient vraies:
False
False
False
False- schéma de Kutta \( \begin{array}{c|ccc} 0 & 0 & 0 & 0 \\ \frac{1}{2} & \frac{1}{2} & 0&0\\ 1 & -1 &2&0\\ \hline & \frac{1}{6} & \frac{2}{3} & \frac{1}{6} \end{array} \quad \implies \begin{cases} u_0 = y_0 \\ K_1 = \varphi\left(t_n,u_n\right)\\ K_2 = \varphi\left(t_n+\frac{h}{2},u_n+\frac{h}{2}K_1\right)\\ K_3 = \varphi\left(t_{n+1},u_n+h(-K_1+2K_2)\right)\\ u_{n+1} = u_n + \frac{h}{6}\left(K_1+4K_2+K_3\right) & n=0,1,\dots N-1 \end{cases} \)
Étant une méthode explicite à 3 étapes, elle a au mieux d’ordre 3. On vérifie ci-dessous qu’elle est d’ordre 3:
Code
c = [0, sympy.S(1)/2, 1]
b = [sympy.S(1)/6, sympy.S(2)/3, sympy.S(1)/6]
A = [[0, 0, 0],
[sympy.S(1)/2, 0, 0],
[-1, 2, 0]]
s = len(c)
print("🌟 Consistance")
print(sum(b)==1)
for i in range(s):
print(sum(A[i])==c[i])
print("\n🌟 Pour être d'ordre 2 il faut que la condition suivante soit vraie:")
print(sum([b[i]*c[i] for i in range(s)]).simplify()==sympy.Rational(1,2))
print("\n🌟 Pour être d'ordre 3 il faut que les conditions suivantes soient vraies:")
print(sum([b[i]*c[i]**2 for i in range(s)]).simplify()==sympy.Rational(1,3))
print(sum([b[i]*A[i][j]*c[j] for i in range(s) for j in range(s)]).simplify()==sympy.Rational(1,6))
print("\n🌟 Pour être d'ordre 4 il faut que les conditions suivantes soient vraies:")
print(sum([b[i]*c[i]**3 for i in range(s)]).simplify()==sympy.Rational(1,4))
print(sum([b[i]*c[i]*A[i][j]*c[j] for i in range(s) for j in range(s)]).simplify()==sympy.Rational(1,8))
print(sum([b[i]*A[i][j]*c[j]**2 for i in range(s) for j in range(s)]).simplify()==sympy.Rational(1,12))
print(sum([b[i]*A[i][j]*A[j][k]*c[k] for i in range(s) for j in range(s) for k in range(s)]).simplify()==sympy.Rational(1,24))🌟 Consistance
True
True
True
True
🌟 Pour être d'ordre 2 il faut que la condition suivante soit vraie:
True
🌟 Pour être d'ordre 3 il faut que les conditions suivantes soient vraies:
True
True
🌟 Pour être d'ordre 4 il faut que les conditions suivantes soient vraies:
True
False
True
False- schéma \( \begin{array}{c|ccc} 0 & 0 & 0 & 0 \\ \frac{1}{2} & \frac{1}{2} & 0&0\\ 1 & -1 &2&0\\ \hline & -\frac{1}{6} & \frac{4}{3} & -\frac{1}{6} \end{array} \quad \implies \begin{cases} u_0 = y_0 \\ K_1 = \varphi\left(t_n,u_n\right)\\ K_2 = \varphi\left(t_n+\frac{h}{2},u_n+\frac{h}{2}K_1\right)\\ K_3 = \varphi\left(t_{n+1},u_n+h(-K_1+2K_2)\right)\\ u_{n+1} = u_n + \frac{h}{6}\left(-K_1+8K_2-K_3\right) & n=0,1,\dots N-1 \end{cases} \)
Étant une méthode explicite à 3 étapes, elle a au mieux d’ordre 3. On vérifie ci-dessous qu’elle n’est que d’ordre 2:
Code
c = [0, sympy.Rational(1,2), 1]
b = [-sympy.Rational(1,6), sympy.Rational(4,3), -sympy.Rational(1,6)]
A = [[0, 0, 0], [sympy.Rational(1,2), 0, 0], [-1, 2, 0]]
s = len(c)
print("🌟 Consistance")
print(sum(b)==1)
for i in range(s):
print(sum(A[i])==c[i])
print("\n🌟 Pour être d'ordre 2 il faut que la condition suivante soit vraie:")
print(sum([b[i]*c[i] for i in range(s)]).simplify()==sympy.Rational(1,2))
print("\n🌟 Pour être d'ordre 3 il faut que les conditions suivantes soient vraies:")
print(sum([b[i]*c[i]**2 for i in range(s)]).simplify()==sympy.Rational(1,3))
print(sum([b[i]*A[i][j]*c[j] for i in range(s) for j in range(s)]).simplify()==sympy.Rational(1,6))🌟 Consistance
True
True
True
True
🌟 Pour être d'ordre 2 il faut que la condition suivante soit vraie:
True
🌟 Pour être d'ordre 3 il faut que les conditions suivantes soient vraies:
False
False- schéma Radau-IIa (d’ordre 5) \( \begin{array}{c|ccc} \frac{4-\sqrt{6}}{10} & \frac{88-7\sqrt{6}}{360} & \frac{296-169\sqrt{6}}{1800} & \frac{-2+3\sqrt{6}}{225} \\ \frac{4+\sqrt{6}}{10} & \frac{296+169\sqrt{6}}{1800} & \frac{88+7\sqrt{6}}{360}&\frac{-2-3\sqrt{6}}{225}\\ 1 & \frac{16-\sqrt{6}}{36} &\frac{16+\sqrt{6}}{36}&\frac{1}{9}\\ \hline & \frac{16-\sqrt{6}}{36} &\frac{16+\sqrt{6}}{36}& \frac{1}{9} \end{array} \quad \implies \begin{cases} u_0 = y_0 \\ K_1 = \varphi\left(t_n+\frac{4-\sqrt{6}}{10}h,u_n+h\left(\frac{88-7\sqrt{6}}{360} K_1+\frac{296-169\sqrt{6}}{1800} K_2+\frac{-2+3\sqrt{6}}{225}K_3\right)\right)\\ K_2 = \varphi\left(t_n+\frac{4+\sqrt{6}}{10}h,u_n+h\left(\frac{296+169\sqrt{6}}{1800}K_1+\frac{88+7\sqrt{6}}{360}K_2+\frac{-2-3\sqrt{6}}{225}K_3\right)\right)\\ K_3 = \varphi\left(t_n+h,u_n+h\left(\frac{16-\sqrt{6}}{36}K_1+\frac{16+\sqrt{6}}{36}K_2+\frac{1}{9}K_3\right)\right)\\ u_{n+1} = u_n + h\left(\frac{16-\sqrt{6}}{36}K_1+\frac{16+\sqrt{6}}{36}K_2+\frac{1}{9}K_3\right) & n=0,1,\dots N-1 \end{cases} \) Notons que \(c_s=1\) et \(a_{sj}=b_j\) pour tout \(j=1,\dots,s\) ainsi \(K_s=\varphi(t_{n+1},u_{n+1})\).
Étant une méthode implicite à 3 étapes, elle a au mieux d’ordre 6. On vérifie ci-dessous qu’elle est d’ordre 5:
Code
sq6 = sympy.sqrt(6)
c = [(4-sq6)/10, (4+sq6)/10, 1]
b = [(16-sq6)/36, (16+sq6)/36, sympy.Rational(1,9)]
A = [[(88-7*sq6)/360, (296-169*sq6)/1800, (-2+3*sq6)/225],
[(296+169*sq6)/1800, (88+7*sq6)/360, (-2-3*sq6)/225],
[(16-sq6)/36, (16+sq6)/36,sympy.S(1)/9] ]
s = len(c)
print("🌟 Consistance")
print(sum(b)==1)
for i in range(s):
print(sum(A[i])==c[i])
print("\n🌟 Pour être d'ordre 2 il faut que la condition suivante soit vraie:")
print(sum([b[i]*c[i] for i in range(s)]).simplify()==sympy.Rational(1,2))
print("\n🌟 Pour être d'ordre 3 il faut que les conditions suivantes soient vraies:")
print(sum([b[i]*c[i]**2 for i in range(s)]).simplify()==sympy.Rational(1,3))
print(sum([b[i]*A[i][j]*c[j] for i in range(s) for j in range(s)]).simplify()==sympy.Rational(1,6))
print("\n🌟 Pour être d'ordre 4 il faut que les conditions suivantes soient vraies:")
print(sum([b[i]*c[i]**3 for i in range(s)]).simplify()==sympy.Rational(1,4))
print(sum([b[i]*c[i]*A[i][j]*c[j] for i in range(s) for j in range(s)]).simplify()==sympy.Rational(1,8))
print(sum([b[i]*A[i][j]*c[j]**2 for i in range(s) for j in range(s)]).simplify()==sympy.Rational(1,12))
print(sum([b[i]*A[i][j]*A[j][k]*c[k] for i in range(s) for j in range(s) for k in range(s)]).simplify()==sympy.Rational(1,24))🌟 Consistance
True
True
True
True
🌟 Pour être d'ordre 2 il faut que la condition suivante soit vraie:
True
🌟 Pour être d'ordre 3 il faut que les conditions suivantes soient vraies:
True
True
🌟 Pour être d'ordre 4 il faut que les conditions suivantes soient vraies:
True
True
True
True8 Exemples à 4 étages explicites
Un schéma RK à \(4\) étages explicite a pour matrice de Butcher \( \begin{array}{c|cccc} 0 & 0 & 0 & 0 & 0\\ c_2 & a_{21} & 0&0&0\\ c_3 & a_{31} &a_{32}&0&0\\ c_4 & a_{41} &a_{42}&a_{43}&0\\ \hline & b_1 & b_2 & b_3 & b_4 \end{array} \text{ avec } \begin{cases} c_2=a_{21}\\ c_3=a_{31}+a_{32}\\ c_4=a_{41}+a_{42}+a_{43}\\ b_1+b_2+b_3+b_4=1 \end{cases} \quad \implies \begin{cases} u_0 = y_0 \\ K_1 = \varphi\left(t_n,u_n\right)\\ K_2 = \varphi\left(t_n+hc_2,u_n+h(a_{21}K_1)\right)\\ K_3 = \varphi\left(t_n+hc_3,u_n+h(a_{31}K_1+ a_{32}K_2)\right)\\ K_4 = \varphi\left(t_n+hc_4,u_n+h(a_{41}K_1+ a_{42}K_2+ a_{43}K_3)\right)\\ u_{n+1} = u_n + h\left(b_1K_1+b_2K_2+b_3K_3+b_4K_4\right) & n=0,1,\dots N-1 \end{cases} \)
Voici deux exemples (le premier est le plus connus):
- schéma RK4-1 (“La” méthode de Runge-Kutta) \( \begin{array}{c|cccc} 0 & 0 & 0 & 0 & 0\\ \frac{1}{2} & \frac{1}{2} & 0 & 0 & 0\\ \frac{1}{2} & 0 &\frac{1}{2} &0&0\\ 1 & 0 & 0 & 1 & 0\\ \hline & \frac{1}{6} & \frac{1}{3} & \frac{1}{3} & \frac{1}{6} \end{array} \quad \implies \begin{cases} u_0 = y_0 \\ K_1 = \varphi\left(t_n,u_n\right)\\ K_2 = \varphi\left(t_n+\frac{h}{2},u_n+\frac{h}{2} K_1)\right)\\ K_3 = \varphi\left(t_n+\frac{h}{2},u_n+\frac{h}{2}K_2\right)\\ K_4 = \varphi\left(t_{n+1},u_n+h K_3\right)\\ u_{n+1} = u_n + \frac{h}{6}\left(K_1+2K_2+2K_3+K_4\right) & n=0,1,\dots N-1 \end{cases} \) Il est bien d’ordre 4:
Code
c = [0, sympy.Rational(1,2), sympy.Rational(1,2), 1]
b = [sympy.Rational(1,6), sympy.Rational(1,3), sympy.Rational(1,3), sympy.Rational(1,6)]
A = [[0, 0, 0, 0],
[sympy.Rational(1,2), 0, 0, 0],
[0, sympy.Rational(1,2), 0, 0],
[0, 0, 1, 0]]
s = len(c)
print("🌟 Consistance")
print(sum(b)==1)
for i in range(s):
print(sum(A[i])==c[i])
print("\n🌟 Pour être d'ordre 2 il faut que la condition suivante soit vraie:")
print(sum([b[i]*c[i] for i in range(s)]).simplify()==sympy.Rational(1,2))
print("\n🌟 Pour être d'ordre 3 il faut que les conditions suivantes soient vraies:")
print(sum([b[i]*c[i]**2 for i in range(s)]).simplify()==sympy.Rational(1,3))
print(sum([b[i]*A[i][j]*c[j] for i in range(s) for j in range(s)]).simplify()==sympy.Rational(1,6))
print("\n🌟 Pour être d'ordre 4 il faut que les conditions suivantes soient vraies:")
print(sum([b[i]*c[i]**3 for i in range(s)]).simplify()==sympy.Rational(1,4))
print(sum([b[i]*c[i]*A[i][j]*c[j] for i in range(s) for j in range(s)]).simplify()==sympy.Rational(1,8))
print(sum([b[i]*A[i][j]*c[j]**2 for i in range(s) for j in range(s)]).simplify()==sympy.Rational(1,12))
print(sum([b[i]*A[i][j]*A[j][k]*c[k] for i in range(s) for j in range(s) for k in range(s)]).simplify()==sympy.Rational(1,24))🌟 Consistance
True
True
True
True
True
🌟 Pour être d'ordre 2 il faut que la condition suivante soit vraie:
True
🌟 Pour être d'ordre 3 il faut que les conditions suivantes soient vraies:
True
True
🌟 Pour être d'ordre 4 il faut que les conditions suivantes soient vraies:
True
True
True
True- schéma RK4-2 \( \begin{array}{c|cccc} 0 & 0 & 0 & 0 & 0\\ \frac{1}{4} & \frac{1}{4} & 0 & 0 & 0\\ \frac{1}{2} & 0 &\frac{1}{2} &0&0\\ 1 & 1 & -2 & 2 & 0\\ \hline & \frac{1}{6} & 0 & \frac{2}{3} & \frac{1}{6} \end{array} \quad \implies \begin{cases} u_0 = y_0 \\ K_1 = \varphi\left(t_n,u_n\right)\\ K_2 = \varphi\left(t_n+\frac{h}{4},u_n+\frac{h}{4} K_1)\right)\\ K_3 = \varphi\left(t_n+\frac{h}{2},u_n+\frac{h}{2}K_2\right)\\ K_4 = \varphi\left(t_{n+1},u_n+h (K_1-2K_2+2K_3)\right)\\ u_{n+1} = u_n + \frac{h}{6}\left(K_1+4K_3+K_4\right) & n=0,1,\dots N-1 \end{cases} \) Il est bien d’ordre 4:
Code
c = [0, sympy.Rational(1,4), sympy.Rational(1,2), 1]
b = [sympy.Rational(1,6), 0, sympy.Rational(2,3), sympy.Rational(1,6)]
A = [ [0, 0, 0, 0],
[sympy.Rational(1,4), 0, 0, 0],
[0, sympy.Rational(1,2), 0, 0],
[1, -2, 2, 0] ]
s = len(c)
print("🌟 Consistance")
print(sum(b)==1)
for i in range(s):
print(sum(A[i])==c[i])
print("\n🌟 Pour être d'ordre 2 il faut que la condition suivante soit vraie:")
print(sum([b[i]*c[i] for i in range(s)]).simplify()==sympy.Rational(1,2))
print("\n🌟 Pour être d'ordre 3 il faut que les conditions suivantes soient vraies:")
print(sum([b[i]*c[i]**2 for i in range(s)]).simplify()==sympy.Rational(1,3))
print(sum([b[i]*A[i][j]*c[j] for i in range(s) for j in range(s)]).simplify()==sympy.Rational(1,6))
print("\n🌟 Pour être d'ordre 4 il faut que les conditions suivantes soient vraies:")
print(sum([b[i]*c[i]**3 for i in range(s)]).simplify()==sympy.Rational(1,4))
print(sum([b[i]*c[i]*A[i][j]*c[j] for i in range(s) for j in range(s)]).simplify()==sympy.Rational(1,8))
print(sum([b[i]*A[i][j]*c[j]**2 for i in range(s) for j in range(s)]).simplify()==sympy.Rational(1,12))
print(sum([b[i]*A[i][j]*A[j][k]*c[k] for i in range(s) for j in range(s) for k in range(s)]).simplify()==sympy.Rational(1,24))🌟 Consistance
True
True
True
True
True
🌟 Pour être d'ordre 2 il faut que la condition suivante soit vraie:
True
🌟 Pour être d'ordre 3 il faut que les conditions suivantes soient vraies:
True
True
🌟 Pour être d'ordre 4 il faut que les conditions suivantes soient vraies:
True
True
True
True- schéma RK4-3 (règle 3/8) \( \begin{array}{c|cccc} 0 & 0 & 0 & 0 & 0\\ \frac{1}{3} & \frac{1}{3} & 0 & 0 & 0\\ \frac{2}{3} &-\frac{1}{3} & 1 &0&0\\ 1 & 1 & -1 & 1 & 0\\ \hline & \frac{1}{8} & \frac{3}{8} & \frac{3}{8} & \frac{1}{8} \end{array} \quad \implies \begin{cases} u_0 = y_0 \\ K_1 = \varphi\left(t_n,u_n\right)\\ K_2 = \varphi\left(t_n+\frac{h}{3},u_n+\frac{h}{3} K_1)\right)\\ K_3 = \varphi\left(t_n+\frac{2}{3}h,u_n+\frac{h}{3}(-K_1+3K_2)\right)\\ K_4 = \varphi\left(t_{n+1},u_n+h (K_1-K_2+K_3)\right)\\ u_{n+1} = u_n + \frac{h}{8}\left(K_1+3K_2+3K_3+K_4\right) & n=0,1,\dots N-1 \end{cases} \) Il est bien d’ordre 4:
Code
c = [0, sympy.Rational(1,3), sympy.Rational(2,3), 1]
b = [sympy.Rational(1,8), sympy.Rational(3,8), sympy.Rational(3,8), sympy.Rational(1,8)]
A = [ [0, 0, 0, 0],
[sympy.Rational(1,3), 0, 0, 0],
[-sympy.Rational(1,3), 1, 0, 0],
[1, -1, 1, 0] ]
s = len(c)
print("🌟 Consistance")
print(sum(b)==1)
for i in range(s):
print(sum(A[i])==c[i])
print("\n🌟 Pour être d'ordre 2 il faut que la condition suivante soit vraie:")
print(sum([b[i]*c[i] for i in range(s)]).simplify()==sympy.Rational(1,2))
print("\n🌟 Pour être d'ordre 3 il faut que les conditions suivantes soient vraies:")
print(sum([b[i]*c[i]**2 for i in range(s)]).simplify()==sympy.Rational(1,3))
print(sum([b[i]*A[i][j]*c[j] for i in range(s) for j in range(s)]).simplify()==sympy.Rational(1,6))
print("\n🌟 Pour être d'ordre 4 il faut que les conditions suivantes soient vraies:")
print(sum([b[i]*c[i]**3 for i in range(s)]).simplify()==sympy.Rational(1,4))
print(sum([b[i]*c[i]*A[i][j]*c[j] for i in range(s) for j in range(s)]).simplify()==sympy.Rational(1,8))
print(sum([b[i]*A[i][j]*c[j]**2 for i in range(s) for j in range(s)]).simplify()==sympy.Rational(1,12))
print(sum([b[i]*A[i][j]*A[j][k]*c[k] for i in range(s) for j in range(s) for k in range(s)]).simplify()==sympy.Rational(1,24))🌟 Consistance
True
True
True
True
True
🌟 Pour être d'ordre 2 il faut que la condition suivante soit vraie:
True
🌟 Pour être d'ordre 3 il faut que les conditions suivantes soient vraies:
True
True
🌟 Pour être d'ordre 4 il faut que les conditions suivantes soient vraies:
True
True
True
True9 Exemple à 5 étages explicite
Un schéma RK à \(5\) étages explicite a pour matrice de Butcher \( \begin{array}{c|ccccc} 0 & 0 & 0 & 0 & 0 &0 \\ c_2 & a_{21} & 0&0&0&0\\ c_3 & a_{31} &a_{32}&0&0&0\\ c_4 & a_{41} &a_{42}&a_{43}&0&0\\ c_5 & a_{51} &a_{52}&a_{53}&a_{54}&0\\ \hline & b_1 & b_2 & b_3 & b_4 & b_5 \end{array} \quad \implies \begin{cases} u_0 = y_0 \\ K_1 = \varphi\left(t_n,u_n\right)\\ K_2 = \varphi\left(t_n+hc_2,u_n+h(a_{21}K_1)\right)\\ K_3 = \varphi\left(t_n+hc_3,u_n+h(a_{31}K_1+ a_{32}K_2\right)\\ K_4 = \varphi\left(t_n+hc_4,u_n+h(a_{41}K_1+ a_{42}K_2+ a_{43}K_3)\right)\\ K_5 = \varphi\left(t_n+hc_5,u_n+h(a_{51}K_1+ a_{52}K_2+ a_{53}K_3+ a_{54}K_4)\right)\\ u_{n+1} = u_n + h\left(b_1K_1+b_2K_2+b_3K_3+b_4K_4+b_5K_5\right) & n=0,1,\dots N-1 \end{cases} \) avec \( \begin{cases} c_2=a_{21}\\ c_3=a_{31}+a_{32}\\ c_4=a_{41}+a_{42}+a_{43}\\ c_5=a_{51}+a_{52}+a_{53}+a_{54}\\ b_1+b_2+b_3+b_4+b_5=1 \end{cases} \)
Voici un exemple:
- schéma de Merson \( \begin{array}{c|ccccc} 0 & 0 & 0 & 0 & 0 &0 \\ \frac{1}{3} & \frac{1}{3} & 0&0&0&0\\ \frac{1}{3} & \frac{1}{6} &\frac{1}{6}&0&0&0\\ \frac{1}{2} & \frac{1}{8} &0&\frac{3}{8}&0&0\\ 1 & \frac{1}{2} &0&-\frac{3}{2}&2&0\\ \hline & \frac{1}{6} & 0 & 0 & \frac{2}{3} & \frac{1}{6} \end{array} \quad \implies \begin{cases} u_0 = y_0 \\ K_1 = \varphi\left(t_n,u_n\right)\\ K_2 = \varphi\left(t_n+\frac{h}{3},u_n+\frac{h}{3}K_1\right)\\ K_3 = \varphi\left(t_n+\frac{h}{3},u_n+\frac{h}{6}(K_1+K_2)\right)\\ K_4 = \varphi\left(t_n+\frac{h}{2},u_n+\frac{h}{8}(K_1+3K_3)\right)\\ K_5 = \varphi\left(t_n+h ,u_n+\frac{h}{2}(K_1-3K_3+4K_4)\right)\\ u_{n+1} = u_n + \frac{h}{6}\left(K_1+4K_4+K_5\right) & n=0,1,\dots N-1 \end{cases} \)
Code
c = [0, sympy.Rational(1,3), sympy.Rational(1,3), sympy.Rational(1,2), 1]
b = [sympy.Rational(1,6), 0, 0, sympy.Rational(2,3), sympy.Rational(1,6)]
A = [[0, 0, 0, 0, 0], [sympy.Rational(1,3), 0, 0, 0, 0], [sympy.Rational(1,6), sympy.Rational(1,6), 0, 0, 0], [sympy.Rational(1,8), 0, sympy.Rational(3,8), 0, 0], [sympy.Rational(1,2), 0, -sympy.Rational(3,2), 2, 0]]
s = len(c)
print("🌟 Consistance")
print(sum(b)==1)
for i in range(s):
print(sum(A[i])==c[i])
print("\n🌟 Pour être d'ordre 2 il faut que la condition suivante soit vraie:")
print(sum([b[i]*c[i] for i in range(s)]).simplify()==sympy.Rational(1,2))
print("\n🌟 Pour être d'ordre 3 il faut que les conditions suivantes soient vraies:")
print(sum([b[i]*c[i]**2 for i in range(s)]).simplify()==sympy.Rational(1,3))
print(sum([b[i]*A[i][j]*c[j] for i in range(s) for j in range(s)]).simplify()==sympy.Rational(1,6))
print("\n🌟 Pour être d'ordre 4 il faut que les conditions suivantes soient vraies:")
print(sum([b[i]*c[i]**3 for i in range(s)]).simplify()==sympy.Rational(1,4))
print(sum([b[i]*c[i]*A[i][j]*c[j] for i in range(s) for j in range(s)]).simplify()==sympy.Rational(1,8))
print(sum([b[i]*A[i][j]*c[j]**2 for i in range(s) for j in range(s)]).simplify()==sympy.Rational(1,12))
print(sum([b[i]*A[i][j]*A[j][k]*c[k] for i in range(s) for j in range(s) for k in range(s)]).simplify()==sympy.Rational(1,24))
print("\n🌟 Pour être d'ordre 5 il faut que les conditions suivantes soient vraies:")
print(sum([b[i]*c[i]**4 for i in range(s)]) == sympy.Rational(1,5))
print(sum([b[i]*c[i]**2*(1-c[i]) for i in range(s)]) + sum([b[i]*A[i][j]*c[j]*(2*c[i]-c[j]) for i in range(s) for j in range(s)]) == sympy.Rational(1,4))🌟 Consistance
True
True
True
True
True
True
🌟 Pour être d'ordre 2 il faut que la condition suivante soit vraie:
True
🌟 Pour être d'ordre 3 il faut que les conditions suivantes soient vraies:
True
True
🌟 Pour être d'ordre 4 il faut que les conditions suivantes soient vraies:
True
True
True
True
🌟 Pour être d'ordre 5 il faut que les conditions suivantes soient vraies:
False
True10 Exemple à 6 étages explicite
Un schéma RK à \(6\) étages explicite a pour matrice de Butcher \( \begin{array}{c|cccccc} 0 & 0 & 0 & 0 & 0 &0&0 \\ c_2 & a_{21} & 0&0&0&0&0\\ c_3 & a_{31} &a_{32}&0&0&0&0\\ c_4 & a_{41} &a_{42}&a_{43}&0&0&0\\ c_5 & a_{51} &a_{52}&a_{53}&a_{54}&0&0\\ c_6 & a_{61} &a_{62}&a_{63}&a_{64}&a_{65}&0\\ \hline & b_1 & b_2 & b_3 & b_4 & b_5&b_6 \end{array} \quad \implies \begin{cases} u_0 = y_0 \\ K_1 = \varphi\left(t_n,u_n\right)\\ K_2 = \varphi\left(t_n+hc_2,u_n+h(a_{21}K_1)\right)\\ K_3 = \varphi\left(t_n+hc_3,u_n+h(a_{31}K_1+ a_{32}K_2\right)\\ K_4 = \varphi\left(t_n+hc_4,u_n+h(a_{41}K_1+ a_{42}K_2+ a_{43}K_3)\right)\\ K_5 = \varphi\left(t_n+hc_5,u_n+h(a_{51}K_1+ a_{52}K_2+ a_{53}K_3+ a_{54}K_4)\right)\\ K_6 = \varphi\left(t_n+hc_6,u_n+h(a_{61}K_1+ a_{62}K_2+ a_{63}K_3+ a_{64}K_4+ a_{65}K_5)\right)\\ u_{n+1} = u_n + h\left(b_1K_1+b_2K_2+b_3K_3+b_4K_4+b_5K_5+b_6K_6\right) & n=0,1,\dots N-1 \end{cases} \) avec \( \begin{cases} c_2=a_{21}\\ c_3=a_{31}+a_{32}\\ c_4=a_{41}+a_{42}+a_{43}\\ c_5=a_{51}+a_{52}+a_{53}+a_{54}\\ c_6=a_{61}+a_{62}+a_{63}+a_{64}+a_{65}\\ b_1+b_2+b_3+b_4+b_5+b_6=1 \end{cases} \)
Voici un exemple:
- schéma de Butcher (d’ordre 5) \( \begin{array}{c|cccccc} 0 & 0 & 0 & 0 & 0 &0&0 \\ \frac{1}{4} & \frac{1}{4} & 0&0&0&0&0\\ \frac{1}{4} & \frac{1}{8} &\frac{1}{8}&0&0&0&0\\ \frac{1}{2} & 0 &-\frac{1}{2}&1&0&0&0\\ \frac{3}{4} & \frac{3}{16} &0&0&\frac{9}{16}&0&0\\ 1 & \frac{-3}{7} &\frac{2}{7}&\frac{12}{7}&\frac{-12}{7}&\frac{8}{7}&0\\ \hline & \frac{7}{90} & 0&\frac{32}{90} & \frac{12}{90} & \frac{32}{90} & \frac{7}{90} \end{array} \quad \implies \begin{cases} u_0 = y_0 \\ K_1 = \varphi\left(t_n,u_n\right)\\ K_2 = \varphi\left(t_n+\frac{h}{4},u_n+\frac{h}{4}K_1\right)\\ K_3 = \varphi\left(t_n+\frac{h}{4},u_n+\frac{h}{8}(K_1+K_2)\right)\\ K_4 = \varphi\left(t_n+\frac{h}{2},u_n+\frac{h}{2}(-K_2+2K_3)\right)\\ K_5 = \varphi\left(t_n+\frac{3h}{4},u_n+\frac{h}{16}(3K_1+9K_4)\right)\\ K_6 = \varphi\left(t_{n+1},u_n+\frac{h}{7}(-3K_1+2K_2+12K_3-12K_4+8K_5)\right)\\ u_{n+1} = u_n + \frac{h}{90}\left(7K_1+32K_3+12K_4+32K_5+7K_6\right) & n=0,1,\dots N-1 \end{cases} \)
Code
c = [0, sympy.Rational(1,4), sympy.Rational(1,4), sympy.Rational(1,2), sympy.Rational(3,4), 1]
b = [sympy.Rational(7,90), 0, sympy.Rational(32,90), sympy.Rational(12,90), sympy.Rational(32,90), sympy.Rational(7,90)]
A = [[0, 0, 0, 0, 0, 0],
[sympy.Rational(1,4), 0, 0, 0, 0, 0],
[sympy.Rational(1,8), sympy.Rational(1,8), 0, 0, 0, 0],
[0, sympy.Rational(-1,2), 1, 0, 0, 0],
[sympy.Rational(3,16), 0, 0, sympy.Rational(9,16), 0, 0],
[sympy.Rational(-3,7), sympy.Rational(2,7), sympy.Rational(12,7), sympy.Rational(-12,7), sympy.Rational(8,7), 0]]
s = len(c)
print("🌟 Consistance")
print(sum(b)==1)
for i in range(s):
print(sum(A[i])==c[i])
print("\n🌟 Pour être d'ordre 2 il faut que la condition suivante soit vraie:")
print(sum([b[i]*c[i] for i in range(s)]).simplify()==sympy.Rational(1,2))
print("\n🌟 Pour être d'ordre 3 il faut que les conditions suivantes soient vraies:")
print(sum([b[i]*c[i]**2 for i in range(s)]).simplify()==sympy.Rational(1,3))
print(sum([b[i]*A[i][j]*c[j] for i in range(s) for j in range(s)]).simplify()==sympy.Rational(1,6))
print("\n🌟 Pour être d'ordre 4 il faut que les conditions suivantes soient vraies:")
print(sum([b[i]*c[i]**3 for i in range(s)]).simplify()==sympy.Rational(1,4))
print(sum([b[i]*c[i]*A[i][j]*c[j] for i in range(s) for j in range(s)]).simplify()==sympy.Rational(1,8))
print(sum([b[i]*A[i][j]*c[j]**2 for i in range(s) for j in range(s)]).simplify()==sympy.Rational(1,12))
print(sum([b[i]*A[i][j]*A[j][k]*c[k] for i in range(s) for j in range(s) for k in range(s)]).simplify()==sympy.Rational(1,24))
print("\n🌟 Pour être d'ordre 5 il faut que les conditions suivantes soient vraies:")
print(sum([b[i]*c[i]**4 for i in range(s)]) == sympy.Rational(1,5))
print(sum([b[i]*c[i]**2*(1-c[i]) for i in range(s)]) + sum([b[i]*A[i][j]*c[j]*(2*c[i]-c[j]) for i in range(s) for j in range(s)]) == sympy.Rational(1,4))🌟 Consistance
True
True
True
True
True
True
True
🌟 Pour être d'ordre 2 il faut que la condition suivante soit vraie:
True
🌟 Pour être d'ordre 3 il faut que les conditions suivantes soient vraies:
True
True
🌟 Pour être d'ordre 4 il faut que les conditions suivantes soient vraies:
True
True
True
True
🌟 Pour être d'ordre 5 il faut que les conditions suivantes soient vraies:
True
True11 Méthodes adapatatives
Pour une méthode donnée, il n’est pas évident de déterminer si le pas \(h\) choisi est optimal : il faut qu’il soit suffisamment petit pour garantir une précision suffisante, mais pas trop petit pour éviter de surcharger inutilement le calcul. Par ailleurs, la solution que l’on cherche à approcher peut nécessiter un pas \(h\) petit à certains endroits et plus grand à d’autres. Ansi, si l’on accepte l’idée d’utiliser une discrétisation non uniforme, on peut décider de construire une méthode qui choisit à chaque itération \(n\) la taille du pas d’intégration \(h\), potentiellement différents à chaque itération. Pour ce faire, on a besoin d’estimer l’erreur \(\varepsilon_{n}\) que l’on commet lorsque l’on effectue une itération du schéma, afin de le comparer à une erreur «acceptable» “tol” : si \(\varepsilon_n\le \text{tol}\), on pourra augmenter la taille du pas d’intégration (si possible), et si au contraire \(\varepsilon_n> \text{tol}\), la dernière étape effectuée n’est pas acceptable, la taille du pas est diminuée et on répète les deux calculs.
Ce procédé, appelé adaptation du pas de discrétisation, est efficace mais nécessite d’avoir un bon estimateur d’erreur locale. En général, il s’agit d’un estimateur d’erreur a posteriori, car les estimateurs d’erreur a priori sont trop compliqués en pratique. On peut construire l’estimateur d’erreur de deux manières :
- en utilisant un unique schéma, mais avec deux pas de discrétisation différents ;
- en utilisant deux schémas d’ordre différent.
11.1 CAS 1 : un unique schéma, mais avec deux pas de discrétisation différents
Une méthode courante pour garantir la précision dans la résolution d’un problème de Cauchy est de résoudre le problème deux fois en utilisant des pas \(h\) et \(h/2\), puis de comparer les approximations obtenues aux points de maillage correspondant à la grille la plus grossière. Autrement dit, à chaque étape, deux approximations différentes de la solution sont calculées
- on calcule \(u_{n+1}\) avec un pas \(h\) donné,
- on calcule également \(\hat u_{n+1}\) avec un pas \(h/2\) de la même méthode (ce qui nécessite deux étapes pour que cela corresponde à l’approximation au même point \(t_n+h\));
L’erreur est donc estimée par la différence entre ces deux approximations : \( \varepsilon_{n+1} = \left| u_{n+1} - \hat u_{n+1} \right| \)
Selon la valeur de \(\varepsilon_{n+1}\), on peut alors décider de doubler \(h\) ou de le diviser par \(2\) pour la prochaine itération.
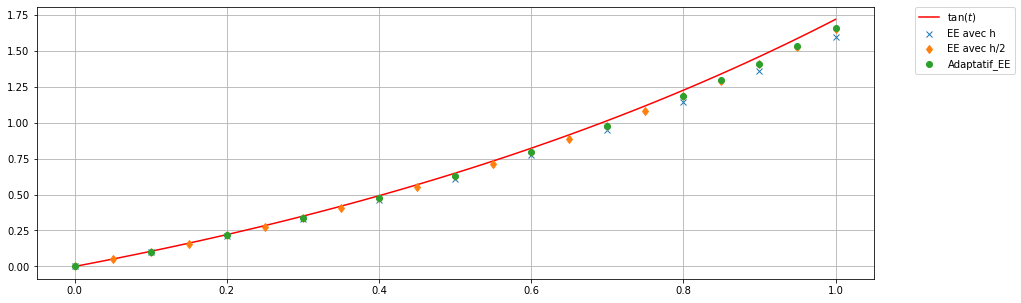
11.1.1 Exemple : méthode d’Euler explicite à pas adaptatif
La méthode d’Euler explicite est bien adaptée à un calcul dynamique du pas de discrétisation \(h\) tenant compte des variations de l’inconnue sur l’intervalle d’intégration. Ici, l’estimateur d’erreur peut être construit à l’aide de deux pas de discrétisation (typiquement \(h\) et \(h/2\)).
Voyons un exemple d’implémentation de la méthode d’Euler explicite à pas adaptatif.
Code
%reset -f
import numpy as np
import matplotlib.pyplot as plt
def EE( phi, tt, y0 ):
h = tt[1]-tt[0]
uu = np.zeros_like(tt)
uu[0] = y0
for n in range(len(tt)-1):
uu[n+1] = uu[n]+h*phi(tt[n],uu[n])
return uu
def Adaptatif_EE( phi, t0, tfinal, y0, tol, hinit, hmin, hmax ):
tt = np.array([t0])
uu = np.array([y0])
uu[0] = y0
h = hinit
n = 0
while tt[n]<tfinal:
# Un pas d'EE avec h
uu_gr = uu[n]+h*phi(tt[n],uu[n])
# Deux pas d'EE avec h/2
v = uu[n]+h/2*phi(tt[n],uu[n])
uu_fi = v+h/2*phi(tt[n]+h/2,v)
erreur = abs(uu_gr-uu_fi)
if erreur< tol/2 or h<hmin:
tt = np.append(tt,tt[n]+h)
uu = np.append(uu,uu_fi)
h = min(2*h,hmax)
n = n+1
else:
h = max(h/2,hmin)
return tt,uu
# ================================
# MAIN
# ================================
t0, tfinal = 0, 1
y0 = 0
phi = lambda t,y : 1+y
sol_exacte = lambda t : np.exp(t)-1
# ================================
# Comparaison des méthodes
# ================================
plt.figure(figsize=(15,5))
# exacte
tt_ex = np.linspace(t0,tfinal,101)
yy = sol_exacte(tt_ex)
plt.plot(tt_ex, yy, 'r',label=r'$\tan(t)$')
# Pas fixe h
tt = np.linspace(t0,tfinal,11)
h_init = tt[1]-tt[0]
uu_EE = EE(phi, tt, y0)
plt.plot(tt,uu_EE, 'x', label='EE avec h')
# Pas fixe h/2
tt2 = np.linspace(t0,tfinal,21)
uu_EE2 = EE(phi, tt2, y0)
plt.plot(tt2,uu_EE2, 'd', label='EE avec h/2')
# Pas adaptatif
tt_adapt, uu_adapt = Adaptatif_EE(phi, t0, tfinal, y0, tol=h_init/10, hinit=h_init, hmin=1e-6, hmax=4*h_init)
plt.plot(tt_adapt,uu_adapt, 'o', label='Adaptatif_EE')
plt.legend(bbox_to_anchor=(1.05, 1), loc='upper left', borderaxespad=0.)
plt.grid();
# ================================
# Comparaison des grilles
# ================================
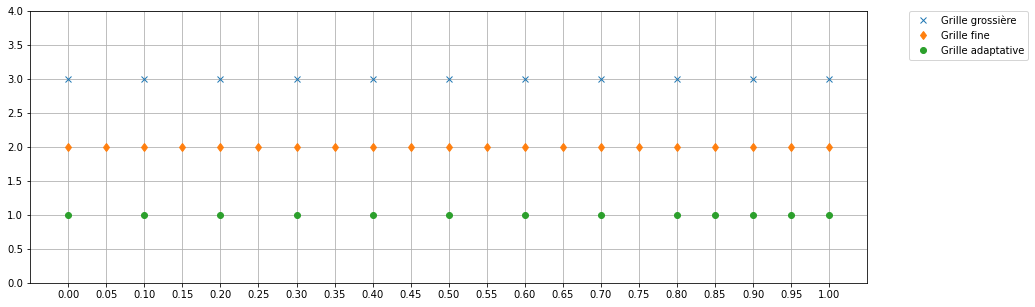
plt.figure(figsize=(15,5))
plt.plot(tt,np.ones_like(tt)*3,'x',label='Grille grossière')
plt.plot(tt2,np.ones_like(tt2)*2,'d',label='Grille fine')
plt.plot(tt_adapt,np.ones_like(tt_adapt),'o',label='Grille adaptative')
plt.legend(bbox_to_anchor=(1.05, 1), loc='upper left', borderaxespad=0.)
plt.ylim(0,4);
plt.xticks(tt2)
plt.grid()
plt.show()
# ================================================================
# Comparaison des approximations en t=tfinal
# ================================================================
from tabulate import tabulate
tab = []
headers = ["Méthode", "t final", "|u(t final) - sol_exacte(tfinzl)|", "Points de grille"]
tab.append(["EE avec h", tt[-1], abs(uu_EE[-1]-sol_exacte(tt[-1])), len(tt)])
tab.append(["EE avec h/2", tt2[-1], abs(uu_EE2[-1]-sol_exacte(tt2[-1])), len(tt2)])
idx = np.argmax(tt_adapt>tfinal)-1
tab.append(["Adaptatif_EE", tt_adapt[idx], abs(uu_adapt[idx]-sol_exacte(tt_adapt[idx])), len(tt_adapt)])
# tab.append(["Exacte", tfinal, sol_exacte(tfinal), ""])
display(tabulate(tab, headers=headers, tablefmt="html", floatfmt=".2e"))
| Méthode | t final | |u(t final) - sol_exacte(tfinzl)| | Points de grille |
|---|---|---|---|
| EE avec h | 1.00e+00 | 1.25e-01 | 11 |
| EE avec h/2 | 1.00e+00 | 6.50e-02 | 21 |
| Adaptatif_EE | 1.00e+00 | 5.87e-02 | 13 |
11.2 CAS 2 : deux schémas d’ordre différent (méthode de Runge-Kutta emboîtée)
Tout comme la méthode d’Euler explicite, les méthodes RK étant à un pas se prêtent bien aux techniques d’adaptation. On peut construire leur estimateur d’erreur de deux manières :
- en utilisant un schéma RK du même ordre, mais avec deux pas de discrétisation différents (comme pour la méthode d’Euler ci-dessus) ;
- en utilisant deux schémas RK d’ordre différent, mais avec le même nombre \(s\) d’étapes et les mêmes coefficients \(a_{ij}\) et \(c_i\) (seules les coefficients \(b_i\) changent entre les deux méthodes).
La méthode de Runge-Kutta emboîtée utilise cette deuxième approche. L’intérêt de ces deux formules emboîtées est de permettre une estimation de l’erreur locale facilement calculable : \( \varepsilon_{n+1} = \left| u_{n+1} - \hat u_{n+1} \right| = h \left| \sum_{i=1}^s (b_i - \hat b_i) K_i \right| \)
11.2.1 Méthode de Runge-Kutta adaptative Euler Explicite/Heun (RK12)
La méthode de Runge-Kutta adaptative la plus simple implique de combiner la méthode de Heun, d’ordre 2, avec la méthode d’Euler explicite, d’ordre 1. Son tableau de Butcher étendu est le suivant : \( \begin{array}{c|cc} 0 & 0 & 0 \\ 1 & 1 & 0 \\ \hline \text{(Heun)}& \frac{1}{2} & \frac{1}{2}\\ \text{(EE)}& 1 & 0 \end{array} \)
Code
%reset -f
import numpy as np
import matplotlib.pyplot as plt
def EE( phi, tt, y0 ):
h = tt[1]-tt[0]
uu = np.zeros_like(tt)
uu[0] = y0
for n in range(len(tt)-1):
k0 = phi(tt[n],uu[n])
k1 = phi(tt[n]+h,uu[n]+h*k0)
uu[n+1] = uu[n]+h*(1*k0+0*k1)
return uu
def HEUN( phi, tt, y0 ):
h = tt[1]-tt[0]
uu = np.zeros_like(tt)
uu[0] = y0
for n in range(len(tt)-1):
k0 = phi(tt[n],uu[n])
k1 = phi(tt[n]+h,uu[n]+h*k0)
uu[n+1] = uu[n]+h*(1/2*k0+1/2*k1)
return uu
def RK12( phi, t0, tfinal, y0, tol, hinit, hmin, hmax ):
tt = np.array([t0])
uu = np.array([y0])
uu[0] = y0
h = hinit
n = 0
while tt[n]<tfinal:
k0 = phi(tt[n],uu[n])
k1 = phi(tt[n]+h,uu[n]+h*k0)
# Un pas de EE
# uu_om = uu[n]+h*(1*k0+0*k1)
# Un pas de HEUN
uu_om_p1 = uu[n]+h*(1/2*k0+1/2*k1)
# choix
erreur = (-1/2*k0+1/2*k1)*h
if abs(erreur) < tol/2 or h<hmin:
tt = np.append(tt,tt[n]+h)
uu = np.append(uu,uu_om_p1)
h = min(2*h,hmax)
n = n+1
else:
h = max(h/2,hmin)
if tt[n]+h>tfinal:
h = tfinal-tt[n]
return tt,uu
# ================================
# MAIN
# ================================
t0, tfinal = 0, np.pi/2-0.1
y0 = 0
phi = lambda t,y : 1+y**2
sol_exacte = lambda t : np.tan(t)
# ================================
# Comparaison des méthodes
# ================================
plt.figure(figsize=(15,5))
# exacte
tt_ex = np.linspace(t0,tfinal,101)
yy = sol_exacte(tt_ex)
plt.plot(tt_ex, yy, 'r',label=r'$\tan(t)$')
# Pas fixe h
tt = np.linspace(t0,tfinal,11)
h_init = tt[1]-tt[0]
# EE
uu_EE = EE(phi, tt, y0)
plt.plot(tt,uu_EE, 'x', label='EE')
# HEUN
uu_HEUN = HEUN(phi, tt, y0)
plt.plot(tt,uu_HEUN, 'd', label='HEUN')
# Pas adaptatif
tt_adapt, uu_adapt = RK12(phi, t0, tfinal, y0, tol=1.e-1, hinit=h_init, hmin=1e-3, hmax=4*h_init)
plt.plot(tt_adapt,uu_adapt, 'o', label='Adaptatif_EE')
plt.legend(bbox_to_anchor=(1.05, 1), loc='upper left', borderaxespad=0.)
plt.grid();
# ================================
# Comparaison des grilles
# ================================
plt.figure(figsize=(15,5))
plt.plot(tt,np.ones_like(tt)*2,'x',label='Grille fixe')
plt.plot(tt_adapt,np.ones_like(tt_adapt),'o',label='Grille adaptative')
plt.legend(bbox_to_anchor=(1.05, 1), loc='upper left', borderaxespad=0.)
plt.ylim(0,3);
plt.xticks(tt)
plt.grid()
plt.show()
# ================================================================
# Comparaison des approximations en t=tfinal
# ================================================================
from tabulate import tabulate
tab = []
headers = ["Méthode", "t final", "|u(t final)-exacte(tfinal)|", "Points de grille"]
tab.append(["EE", tt[-1], abs(uu_EE[-1]-sol_exacte(tfinal)), len(tt)])
tab.append(["HEUN", tt[-1], abs(uu_HEUN[-1]-sol_exacte(tfinal)), len(tt)])
idx = np.argmax(tt_adapt>tfinal)-1
tab.append(["RK12", tt_adapt[idx], abs(uu_adapt[idx]-sol_exacte(tfinal)), len(tt_adapt)])
display(tabulate(tab, headers=headers, tablefmt="html", floatfmt=".2e"))

| Méthode | t final | |u(t final)-exacte(tfinal)| | Points de grille |
|---|---|---|---|
| EE | 1.47e+00 | 6.38e+00 | 11 |
| HEUN | 1.47e+00 | 2.50e+00 | 11 |
| RK12 | 1.47e+00 | 1.14e-01 | 30 |
11.2.2 Méthode de Runge-Kutta adaptative Heun/Simpson (RK23)
Une méthode de Runge-Kutta adaptative simple combine la méthode de Heun, d’ordre 2, avec la méthode de Simpso, d’ordre 3. Son tableau de Butcher étendu est le suivant : \( \begin{array}{c|cc} 0 & 0 & 0 & 0\\ 1 & 1 & 0 & 0 \\ \frac{1}{2} & \frac{1}{4} & \frac{1}{4} & 0\\ \hline \text{(Heun)}& \frac{1}{2} & \frac{1}{2} & 0\\ \text{(Simpson)}& \frac{1}{6} & \frac{1}{6} & \frac{4}{6} \end{array} \)
Code
%reset -f
import numpy as np
import matplotlib.pyplot as plt
def coeff_K(phi, h, t, u):
k0 = phi(t,u)
k1 = phi(t+h,u+h*k0)
k2 = phi(t+h/2,u+h/4*k0+h/4*k1)
return k0, k1, k2
def HEUN( phi, tt, y0 ):
h = tt[1]-tt[0]
uu = np.zeros_like(tt)
uu[0] = y0
for n in range(len(tt)-1):
k0, k1, k2 = coeff_K(phi, h, tt[n], uu[n])
uu[n+1] = uu[n]+h*(1/2*k0+1/2*k1)
return uu
def SIMPSON( phi, tt, y0 ):
h = tt[1]-tt[0]
uu = np.zeros_like(tt)
uu[0] = y0
for n in range(len(tt)-1):
k0, k1, k2 = coeff_K(phi, h, tt[n], uu[n])
uu[n+1] = uu[n]+h*(1/6*k0+4/6*k2+1/6*k1)
return uu
def RK23( phi, t0, tfinal, y0, tol, hinit, hmin, hmax ):
tt = np.array([t0])
uu = np.array([y0])
uu[0] = y0
h = hinit
n = 0
while tt[n]<tfinal :
k0, k1, k2 = coeff_K(phi, h, tt[n], uu[n])
# Un pas de Heun
# uu_om = uu[n]+h*(1/2*k0+1/2*k1)
# Un pas de Simpson
uu_om_p1 = uu[n]+h*(1/6*k0+1/6*k1+4/6*k2)
# choix
erreur = h * ( (1/6-1/2)*k0 + (1/6-1/2)*k1 + (4/6-0)*k2 )
if abs(erreur) < tol/2 or h<hmin:
tt = np.append(tt,tt[n]+h)
uu = np.append(uu,uu_om_p1)
h = min(2*h,hmax)
n = n+1
else:
h = max(h/2,hmin)
if tt[n]+h>tfinal:
h = tfinal-tt[n]
return tt,uu
# ================================
# MAIN
# ================================
t0, tfinal = 0, np.pi/2-0.1
y0 = 0
phi = lambda t,y : 1+y**2
sol_exacte = lambda t : np.tan(t)
# ================================
# Comparaison des méthodes
# ================================
plt.figure(figsize=(15,5))
# exacte
tt_ex = np.linspace(t0,tfinal,101)
yy = sol_exacte(tt_ex)
plt.plot(tt_ex, yy, 'r',label=r'$\tan(t)$')
# Pas fixe h
tt = np.linspace(t0,tfinal,11)
h_init = tt[1]-tt[0]
# HEUN
uu_HEUN = HEUN(phi, tt, y0)
plt.plot(tt,uu_HEUN, 'x', label='HEUN')
# SIMPSON
uu_SIMPSON = SIMPSON(phi, tt, y0)
plt.plot(tt,uu_SIMPSON, 'd', label='SIMPSON')
# Pas adaptatif
tt_adapt, uu_adapt = RK23(phi, t0, tfinal, y0, tol=1.e-1, hinit=h_init, hmin=1e-3, hmax=4*h_init)
plt.plot(tt_adapt,uu_adapt, 'o', label='Adaptatif')
plt.legend(bbox_to_anchor=(1.05, 1), loc='upper left', borderaxespad=0.)
plt.grid();
# ================================
# Comparaison des grilles
# ================================
plt.figure(figsize=(15,5))
plt.plot(tt,np.ones_like(tt)*2,'x',label='Grille fixe')
plt.plot(tt_adapt,np.ones_like(tt_adapt),'o',label='Grille adaptative')
plt.legend(bbox_to_anchor=(1.05, 1), loc='upper left', borderaxespad=0.)
plt.ylim(0,3);
plt.xticks(tt)
plt.grid()
plt.show()
# ================================================================
# Comparaison des approximations en t=tfinal
# ================================================================
from tabulate import tabulate
tab = []
headers = ["Méthode", "t final", "|u(t final)-exacte(tfinal)|", "Points de grille"]
tab.append(["HEUN", tt[-1], abs(uu_HEUN[-1]-sol_exacte(tfinal)), len(tt)])
tab.append(["SIMPSON", tt[-1], abs(uu_SIMPSON[-1]-sol_exacte(tfinal)), len(tt)])
idx = np.argmax(tt_adapt>tfinal)-1
tab.append(["RK23", tt_adapt[idx], abs(uu_adapt[idx]-sol_exacte(tt_adapt[idx])), len(tt_adapt)])
display(tabulate(tab, headers=headers, tablefmt="html", floatfmt=".2e"))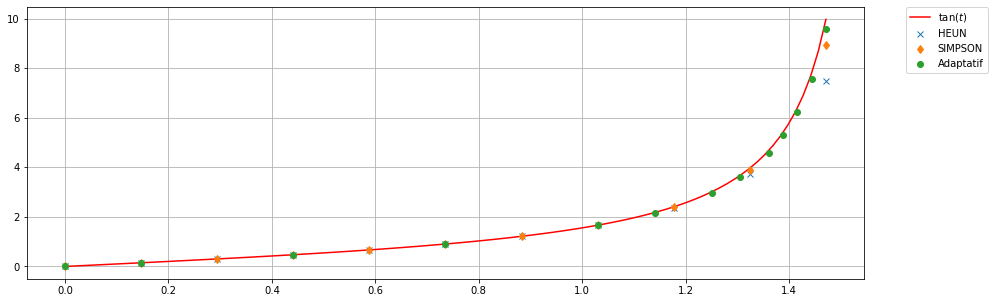

| Méthode | t final | |u(t final)-exacte(tfinal)| | Points de grille |
|---|---|---|---|
| HEUN | 1.47e+00 | 2.50e+00 | 11 |
| SIMPSON | 1.47e+00 | 1.03e+00 | 11 |
| RK23 | 1.47e+00 | 4.00e-01 | 13 |
11.2.3 Méthode de Runge-Kutta adaptative Bogacki/Shampine (ode23)
Une méthode de Runge-Kutta adaptative souvent utilisée combine la méthode de Bogacki avec celle de Shampine. Son tableau de Butcher étendu est le suivant : \( \begin{array}{c|ccc} 0 & 0 & 0 & 0 & 0\\ \frac{1}{2} & \frac{1}{2} & 0 & 0 & 0\\ \frac{3}{4} & 0 & \frac{3}{4} & 0 & 0\\ 1 & \frac{2}{9} & \frac{1}{3} & \frac{4}{9} & 0\\ \hline & \frac{2}{9} & \frac{1}{3} & \frac{4}{9} & 0 \\ & \frac{7}{24} & \frac{1}{4} & \frac{1}{3} & \frac{1}{8} \end{array} \)
Code
%reset -f
import numpy as np
import matplotlib.pyplot as plt
def coeff_K(phi, h, t, u):
k0 = phi(t,u)
k1 = phi(t+h/2,u+h/2*k0)
k2 = phi(t+h*3/4,u+h*3/4*k1)
k3 = phi(t+h,u+h*2/9*k0+h/3*k1+h*4/9*k2)
return k0, k1, k2, k3
def Bogacki( phi, tt, y0 ):
h = tt[1]-tt[0]
uu = np.zeros_like(tt)
uu[0] = y0
for n in range(len(tt)-1):
k0, k1, k2, k3 = coeff_K(phi, h, tt[n], uu[n])
uu[n+1] = uu[n]+h*(2/9*k0+1/3*k1+4/9*k2)
return uu
def Shampine( phi, tt, y0 ):
h = tt[1]-tt[0]
uu = np.zeros_like(tt)
uu[0] = y0
for n in range(len(tt)-1):
k0, k1, k2, k3 = coeff_K(phi, h, tt[n], uu[n])
uu[n+1] = uu[n]+h*(7/24*k0+1/4*k1+1/3*k2+1/8*k3)
return uu
def edo23( phi, t0, tfinal, y0, tol, hinit, hmin, hmax ):
tt = np.array([t0])
uu = np.array([y0])
uu[0] = y0
h = hinit
n = 0
while tt[n]<tfinal :
k0, k1, k2, k3 = coeff_K(phi, h, tt[n], uu[n])
# Un pas de Bogacki
# uu_om = uu[n]+h*(2/9*k0+1/3*k1+4/9*k2)
# Un pas de Shamphine
uu_om_p1 = uu[n]+h*(7/24*k0+1/4*k1+1/3*k2+1/8*k3)
# choix
erreur = h * ( (7/24-2/9)*k0 + (1/4-1/3)*k1 + (1/3-4/9)*k2 + (1/8-0)*k3 )
if abs(erreur) < tol/2 :
tt = np.append(tt,tt[n]+h)
uu = np.append(uu,uu_om_p1)
h = min(2*h,hmax)
n = n+1
else:
h = max(h/2,hmin)
if tt[n]+h>tfinal:
h = tfinal-tt[n]
return tt,uu
# ================================
# MAIN
# ================================
t0, tfinal = 0, np.pi/2-0.1
y0 = 0
phi = lambda t,y : 1+y**2
sol_exacte = lambda t : np.tan(t)
# ================================
# Comparaison des méthodes
# ================================
plt.figure(figsize=(15,5))
# exacte
tt_ex = np.linspace(t0,tfinal,21)
yy = sol_exacte(tt_ex)
plt.plot(tt_ex, yy, 'r',label=r'$\tan(t)$')
# Pas fixe h
tt = np.linspace(t0,tfinal,21)
h_init = tt[1]-tt[0]
# Bogacki
uu_Bogacki = Bogacki(phi, tt, y0)
plt.plot(tt,uu_Bogacki, 'x', label='Bogacki')
# Shampine
uu_Shampine = Shampine(phi, tt, y0)
plt.plot(tt,uu_Shampine, 'd', label='Shampine')
# Pas adaptatif
tt_adapt, uu_adapt = edo23(phi, t0, tfinal, y0, tol=1.e-3, hinit=h_init, hmin=1e-3, hmax=4*h_init)
plt.plot(tt_adapt,uu_adapt, 'o', label='Adaptatif')
plt.legend(bbox_to_anchor=(1.05, 1), loc='upper left', borderaxespad=0.)
plt.grid();
# ================================
# Comparaison des grilles
# ================================
plt.figure(figsize=(15,5))
plt.plot(tt,np.ones_like(tt)*2,'x',label='Grille fixe')
plt.plot(tt_adapt,np.ones_like(tt_adapt),'o',label='Grille adaptative')
plt.legend(bbox_to_anchor=(1.05, 1), loc='upper left', borderaxespad=0.)
plt.ylim(0,3);
plt.xticks(tt)
plt.grid()
plt.show()
# ================================================================
# Comparaison des approximations en t=tfinal
# ================================================================
from tabulate import tabulate
tab = []
headers = ["Méthode", "t final", "|u(t final)-exacte(tfinal)|", "Points de grille"]
tab.append(["Bogacki", tt[-1], abs(uu_Bogacki[-1]-sol_exacte(tfinal)), len(tt)])
tab.append(["Shampine", tt[-1], abs(uu_Shampine[-1]-sol_exacte(tfinal)), len(tt)])
idx = np.argmax(tt_adapt>tfinal)-1
tab.append(["edo23", tt_adapt[idx], abs(uu_adapt[idx]-sol_exacte(tt_adapt[idx])), len(tt_adapt)])
display(tabulate(tab, headers=headers, tablefmt="html", floatfmt=".2e"))

| Méthode | t final | |u(t final)-exacte(tfinal)| | Points de grille |
|---|---|---|---|
| Bogacki | 1.47e+00 | 2.74e-01 | 21 |
| Shampine | 1.47e+00 | 1.74e-01 | 21 |
| edo23 | 1.47e+00 | 1.34e-01 | 38 |
11.2.4 Runge-Kutta-Fehlberg (RKF45) à pas adaptatif
Voici la matrice de Butcher associée à la méthode de Runge-Kutta-Fehlberg (RKF45). Ce tableau représente les coefficients des deux méthodes Runge-Kutta utilisées dans la méthode RK45 pour calculer les coefficients \(k_0\) à \(k_5\), ainsi que les coefficients \(b_0\) à \(b_5\) et \(\hat b_0\) à \(\hat b_5\) utilisés pour combiner les \(K_i\) afin d’obtenir une approximation à l’étape suivante. \( \begin{array}{c|cccccc} 0 & & & & & & \\ \frac{1}{4} & \frac{1}{4} & & & & & \\ \frac{3}{8} & \frac{3}{32} & \frac{9}{32} & & & & \\ \frac{12}{13} & \frac{1932}{2197} & -\frac{7200}{2197} & \frac{7296}{2197} & & & \\ 1 & \frac{439}{216} & -\frac{8}{27} & \frac{3680}{513} & -\frac{845}{4104} & & \\ \frac{1}{2} & -\frac{8}{27} & \frac{2}{9} & -\frac{3544}{2565} & \frac{1859}{4104} & -\frac{11}{40} & \\ \hline & \frac{16}{135} & 0 & \frac{6656}{12825} & \frac{28561}{56430} & -\frac{9}{50} & \frac{2}{55} \\ & \frac{25}{216} & 0 & \frac{1408}{2565} & \frac{2197}{4104} & -\frac{1}{5} & 0 \\ \end{array} \)
Voyons un exemple d’implémentation de la méthode de Runge-Kutta-Fehlberg (RKF45) à pas adaptatif.
Code
%reset -f
import numpy as np
import matplotlib.pyplot as plt
def coeff_K(phi, h, t, u):
k = np.zeros((6,1))
k[0] = phi(t,u)
k[1] = phi(t+h/4,u+h/4*k[0])
k[2] = phi(t+3*h/8,u+3*h/32*k[0]+9*h/32*k[1])
k[3] = phi(t+12*h/13,u+1932*h/2197*k[0]-7200*h/2197*k[1]+7296*h/2197*k[2])
k[4] = phi(t+h,u+439*h/216*k[0]-8*h*k[1]+3680*h/513*k[2]-845*h/4104*k[3])
k[5] = phi(t+h/2,u-8*h/27*k[0]+2*h*k[1]-3544*h/2565*k[2]+1859*h/4104*k[3]-11*h/40*k[4])
return k
def RK4( phi, tt, y0 ):
h = tt[1]-tt[0]
uu = np.zeros_like(tt)
uu[0] = y0
for n in range(len(tt)-1):
k0, k1, k2, k3, k4, k5 = coeff_K(phi, h, tt[n], uu[n])
uu[n+1] = uu[n] + h*( 25/216*k0 + 1408/2565*k2 + 2197/4104*k3 - 1/5*k4 )
return uu
def RK5( phi, tt, y0 ):
h = tt[1]-tt[0]
uu = np.zeros_like(tt)
uu[0] = y0
for n in range(len(tt)-1):
k0, k1, k2, k3, k4, k5 = coeff_K(phi, h, tt[n], uu[n])
uu[n+1] = uu[n] + h* ( 16/135*k0 + 6656/12825*k2 + 28561/56430*k3 -9/50*k4 + 2/55*k5 )
return uu
def RK45( phi, t0, tfinal, y0, tol, hinit, hmin, hmax ):
tt = np.array([t0])
uu = np.array([y0])
uu[0] = y0
h = hinit
n = 0
while tt[n]<tfinal:
k0, k1, k2, k3, k4, k5 = coeff_K(phi, h, tt[n], uu[n])
# Un pas de RK5
uu_om_p1 = uu[n] + h* ( 16/135*k0 + 6656/12825*k2 + 28561/56430*k3 -9/50*k4 + 2/55*k5 )
# choix
erreur = h*( (25/216-16/135)*k0 +
(1408/2565-6656/12825)*k2 +
(2197/4104-28561/56430)*k3 +
(-1/5+9/50)*k4 +(0-2/55)*k5 )
if abs(erreur) < tol/2 or h<hmin:
tt = np.append(tt,tt[n]+h)
uu = np.append(uu,uu_om_p1)
h = min(2*h,hmax)
n = n+1
else:
h = max(h/2,hmin)
if tt[n]+h>tfinal:
h = tfinal-tt[n]
return tt,uu
# ================================
# MAIN
# ================================
# t0, tfinal = 0, np.pi/2-0.1
# y0 = 0
# phi = lambda t,y : 1+y**2
# sol_exacte = lambda t : np.tan(t)
t0, tfinal = 0, 4
y0 = 1
phi = lambda t,y : y*(2-y)
import sympy as sp
t = sp.symbols('t')
y = sp.Function('y')
sol_par = sp.dsolve( sp.Eq(y(t).diff(t), phi(t,y(t)) ) , ics={y(t0): y0} )
display(sol_par)
sol_exacte = sp.lambdify(t,sol_par.rhs,'numpy')
# ================================
# Comparaison des méthodes
# ================================
plt.figure(figsize=(15,5))
# exacte
tt_ex = np.linspace(t0,tfinal,101)
yy = sol_exacte(tt_ex)
plt.plot(tt_ex, yy, 'r',label=r'$\tan(t)$')
# Pas fixe h
tt = np.linspace(t0,tfinal,6)
h_init = tt[1]-tt[0]
# RK4
uu_RK4 = RK4(phi, tt, y0)
plt.plot(tt,uu_RK4, 'v', label='RK4')
# RK5
uu_RK5 = RK5(phi, tt, y0)
plt.plot(tt,uu_RK5, 'd', label='RK5')
# RK45 à pas adaptatif
tt_adapt, uu_adapt = RK45(phi, t0, tfinal, y0, tol=1.e-5, hinit=h_init, hmin=5e-3, hmax=h_init)
plt.plot(tt_adapt,uu_adapt, 'o', label='Adaptatif_EE')
plt.legend(bbox_to_anchor=(1.05, 1), loc='upper left', borderaxespad=0.)
plt.grid();
# ================================
# Comparaison des grilles
# ================================
plt.figure(figsize=(15,5))
plt.plot(tt,np.ones_like(tt)*2,'v',label='Grille grossière')
plt.plot(tt_adapt,np.ones_like(tt_adapt),'o',label='Grille adaptative')
plt.legend(bbox_to_anchor=(1.05, 1), loc='upper left', borderaxespad=0.)
plt.ylim(0,3);
plt.xticks(tt)
plt.grid()
plt.show()
# ================================================================
# Comparaison des approximations en t=tfinal
# ================================================================
from tabulate import tabulate
tab = []
headers = ["Méthode", "t final", "|u(t final)-exacte(tfinal)|", "Points de grille"]
tab.append(["RK4", tt[-1], abs(uu_RK4[-1]-sol_exacte(tfinal)), len(tt)])
tab.append(["RK5", tt[-1], abs(uu_RK5[-1]-sol_exacte(tfinal)), len(tt)])
idx = np.argmax(tt_adapt>tfinal)-1
tab.append(["RK45", tt_adapt[idx], abs(uu_adapt[idx]-sol_exacte(tfinal)), len(tt_adapt)])
display(tabulate(tab, headers=headers, tablefmt="html", floatfmt=".2e"))\(\displaystyle y{\left(t \right)} = \frac{2}{1 + e^{- 2 t}}\)
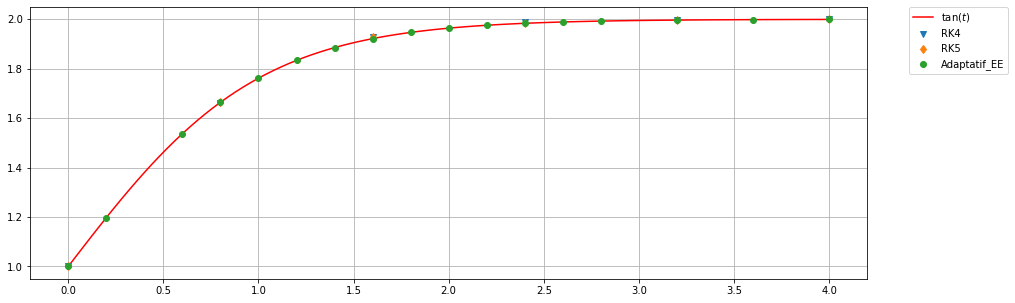

| Méthode | t final | |u(t final)-exacte(tfinal)| | Points de grille |
|---|---|---|---|
| RK4 | 4.00e+00 | 3.36e-04 | 6 |
| RK5 | 4.00e+00 | 1.70e-04 | 6 |
| RK45 | 4.00e+00 | 9.21e-07 | 17 |
11.2.5 Dormand-Prince (DP45) à pas adaptatif
Voici la matrice de Butcher associée à la méthode de Dormand-Prince (DP45). Ce tableau représente les coefficients des deux méthodes Runge-Kutta utilisées dans la méthode RK45 pour calculer les coefficients \(k_0\) à \(k_5\), ainsi que les coefficients \(b_0\) à \(b_5\) et \(\hat b_0\) à \(\hat b_5\) utilisés pour combiner les \(K_i\) afin d’obtenir une approximation à l’étape suivante. \( \begin{array}{c|cccccc} 0 & & & & & & \\ \frac{1}{5} & \frac{1}{5} & & & & & \\ \frac{3}{10} & \frac{3}{40} & \frac{9}{40} & & & & \\ \frac{4}{5} & \frac{44}{45} & -\frac{56}{15} & \frac{32}{9} & & & \\ \frac{8}{9} & \frac{19372}{6561} & -\frac{25360}{2187} & \frac{64448}{6561} & -\frac{212}{729} & & \\ 1 & \frac{9017}{3168} & -\frac{355}{33} & \frac{46732}{5247} & \frac{49}{176} & -\frac{5103}{18656} & \\ 1 & \frac{35}{384} & 0 & \frac{500}{1113} & \frac{125}{192} & -\frac{2187}{6784} & \frac{11}{84} \\ \hline & \frac{35}{384} & 0 & \frac{500}{1113} & \frac{125}{192} & -\frac{2187}{6784} & \frac{11}{84} & 0\\ & \frac{5179}{57600} & 0 & \frac{7571}{16695} & \frac{393}{640} & -\frac{92097}{339200} & \frac{187}{2100} \\ \end{array} \)
Voyons un exemple d’implémentation de la méthode de Runge-Kutta-Fehlberg (RKF45) à pas adaptatif.
Code
%reset -f
import numpy as np
import matplotlib.pyplot as plt
def coeff_K(phi, h, t, u):
k = np.zeros((7,1))
k[0] = phi(t,u)
k[1] = phi(t+h/5,u+h/5*k[0])
k[2] = phi(t+3*h/10,u+3*h/40*k[0]+9*h/40*k[1])
k[3] = phi(t+4*h/5,u+44*h/45*k[0]-56*h/15*k[1]+32*h/9*k[2])
k[4] = phi(t+8*h/9,u+19372*h/6561*k[0]-25360*h/2187*k[1]+64448*h/6561*k[2]-212*h/729*k[3])
k[5] = phi(t+h,u+9017*h/3168*k[0]-355*h/33*k[1]+46732*h/5247*k[2]+49*h/176*k[3]-5103*h/18656*k[4])
k[6] = phi(t+h,u+35*h/384*k[0]+0*k[1]+500*h/1113*k[2]+125*h/192*k[3]-2187*h/6784*k[4]+11*h/84*k[5])
return k
def Dor( phi, tt, y0 ):
h = tt[1]-tt[0]
uu = np.zeros_like(tt)
uu[0] = y0
for n in range(len(tt)-1):
k0, k1, k2, k3, k4, k5, k6 = coeff_K(phi, h, tt[n], uu[n])
uu[n+1] = uu[n] + h*( 35/384*k0 + 0*k1 + 500/1113*k2 + 125/192*k3 - 2187/6784*k4 + 11/84*k5 )
return uu
def Pri( phi, tt, y0 ):
h = tt[1]-tt[0]
uu = np.zeros_like(tt)
uu[0] = y0
for n in range(len(tt)-1):
k0, k1, k2, k3, k4, k5, k6 = coeff_K(phi, h, tt[n], uu[n])
uu[n+1] = uu[n] + h* ( 5179/57600*k0 + 0*k1 + 7571/16695*k2 + 393/640*k3 - 92097/339200*k4 + 187/2100*k5 + 1/40*k6 )
return uu
def DP45( phi, t0, tfinal, y0, tol, hinit, hmin, hmax ):
tt = np.array([t0])
uu = np.array([y0])
uu[0] = y0
h = hinit
n = 0
while tt[n]<tfinal:
k0, k1, k2, k3, k4, k5, k6 = coeff_K(phi, h, tt[n], uu[n])
# Un pas de Pri
# uu_om_p1 = uu[n] + h* ( 5179/57600*k0 + 0*k1 + 7571/16695*k2 + 393/640*k3 - 92097/339200*k4 + 187/2100*k5 + 1/40*k6 )
uu_om_p1 = uu[n] + h*( 35/384*k0 + 0*k1 + 500/1113*k2 + 125/192*k3 - 2187/6784*k4 + 11/84*k5 )
# choix
erreur = h*( (35/384-5179/57600)*k0 +
(0-0)*k1 +
(500/1113-7571/16695)*k2 +
(125/192-393/640)*k3 +
(-2187/6784-92097/339200)*k4 +
(11/84-187/2100)*k5 +
(0-1/40)*k6 )
if abs(erreur) < tol/2 or h<hmin:
tt = np.append(tt,tt[n]+h)
uu = np.append(uu,uu_om_p1)
h = min(2*h,hmax)
n = n+1
else:
h = max(h/2,hmin)
if tt[n]+h>tfinal:
h = tfinal-tt[n]
return tt,uu
# ================================
# MAIN
# ================================
t0, tfinal = 0, 4
y0 = 1
phi = lambda t,y : y*(2-y)
import sympy as sp
t = sp.symbols('t')
y = sp.Function('y')
sol_par = sp.dsolve( sp.Eq(y(t).diff(t), phi(t,y(t)) ) , ics={y(t0): y0} )
display(sol_par)
sol_exacte = sp.lambdify(t,sol_par.rhs,'numpy')
# ================================
# Comparaison des méthodes
# ================================
plt.figure(figsize=(15,5))
# exacte
tt_ex = np.linspace(t0,tfinal,101)
yy = sol_exacte(tt_ex)
plt.plot(tt_ex, yy, 'r',label=r'Exacte')
# Pas fixe h
tt = np.linspace(t0,tfinal,6)
h_init = tt[1]-tt[0]
# Dorman
uu_Dor = Dor(phi, tt, y0)
plt.plot(tt,uu_Dor, 'v', label='Dorman')
# Prince
uu_Pri = Pri(phi, tt, y0)
plt.plot(tt,uu_Pri, 'd', label='Prince')
# DP45 à pas adaptatif
tt_adapt, uu_adapt = DP45(phi, t0, tfinal, y0, tol=1.e-1, hinit=h_init, hmin=h_init/10, hmax=3*h_init)
plt.plot(tt_adapt,uu_adapt, 'o', label='Adaptatif_EE')
plt.legend(bbox_to_anchor=(1.05, 1), loc='upper left', borderaxespad=0.)
plt.grid();
# ================================
# Comparaison des grilles
# ================================
plt.figure(figsize=(15,5))
plt.plot(tt,np.ones_like(tt)*2,'v',label='Grille grossière')
plt.plot(tt_adapt,np.ones_like(tt_adapt),'o',label='Grille adaptative')
plt.legend(bbox_to_anchor=(1.05, 1), loc='upper left', borderaxespad=0.)
plt.ylim(0,3);
plt.xticks(tt)
plt.grid()
plt.show()
# ================================================================
# Comparaison des approximations en t=tfinal
# ================================================================
from tabulate import tabulate
tab = []
headers = ["Méthode", "t final", "|u(t final)-exacte(tfinal)|", "Points de grille"]
tab.append(["Dorman", tt[-1], abs(uu_Dor[-1]-sol_exacte(tfinal)), len(tt)])
tab.append(["Prince", tt[-1], abs(uu_Pri[-1]-sol_exacte(tfinal)), len(tt)])
idx = np.argmax(tt_adapt>tfinal)-1
tab.append(["DP45", tt_adapt[idx], abs(uu_adapt[idx]-sol_exacte(tt_adapt[idx])), len(tt_adapt)])
display(tabulate(tab, headers=headers, tablefmt="html", floatfmt=".2e"))\(\displaystyle y{\left(t \right)} = \frac{2}{1 + e^{- 2 t}}\)
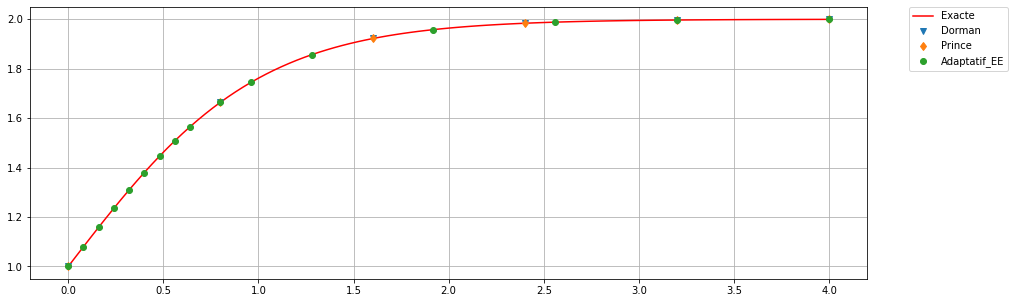

| Méthode | t final | |u(t final)-exacte(tfinal)| | Points de grille |
|---|---|---|---|
| Dorman | 4.00e+00 | 5.59e-05 | 6 |
| Prince | 4.00e+00 | 9.92e-05 | 6 |
| DP45 | 4.00e+00 | 3.57e-05 | 16 |
